電子學/模擬乘法器

模擬乘法器

模擬乘法器是一個電路，其輸出與兩個輸入的乘積成正比

v_{out}=Kv_{1}\cdot v_{2}

其中 K 是一個常數，其量綱為電壓的倒數。一般來說，我們可以預期兩個輸入可以是正的或負的，輸出也可以是正的或負的。然而，大多數實現只在兩個輸入都嚴格為正時才有效：這不是一個很大的限制，因為我們可以對輸入和輸出進行偏移，使核心只處理正訊號，而外部介面則可以處理任何極性（在特定配置下，在一定的限制範圍內）。

將展示兩種可能的實現方式。兩種方法都將使用運算放大器，但第一種方法將使用二極體來獲得所需的關係，第二種方法將使用 MOSFET 電晶體。

二極體實現

眾所周知，使用運算放大器和二極體，很容易獲得某個輸入的對數和指數。記住對數的性質

\log(a\cdot b)=\log a+\log b

我們可以先計算兩個訊號的對數，然後將它們相加，最後計算該和的指數，從而實現兩個訊號的乘積。從數學的角度來看，只要兩個輸入為正數，這種方法就有效，因為負數的對數不存在（在實數域）。我們將會看到，即使原因更“物理”，這種限制對於實際電路也同樣適用。這種實現的框圖如下：

如果我們簡單地將對數、求和和指數電路連線起來，我們將得到以下配置：

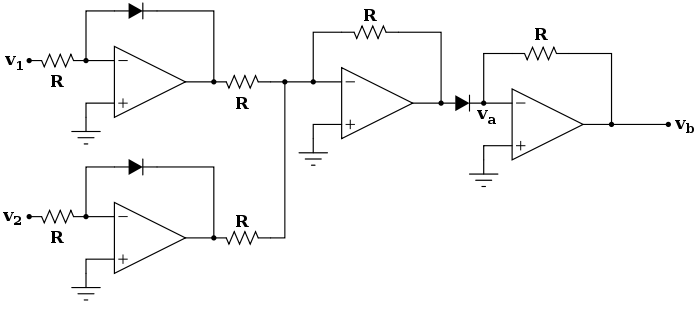
為了快速瞭解電路的行為，我們假設所有電阻 R 的值相同。顯然，可以使用不同的值來獲得不同的結果，但我們在這裡不考慮這種情況。讓我們使用以下符號來表示二極體電流和電壓之間的關係：

i=I_{s}\left(e^{\frac {v}{V_{T}}}-1\right)

其中 $V_{T}={\frac {k*T}{q}}$ 是熱電壓（在常見的執行溫度下為 25..30mV），I_s 是二極體反向偏置時的電流。如果我們在不引入任何近似的情況下分析電路，我們將得到

v_{a}=-\left[-V_{T}\ln \left({\frac {v_{1}}{RI_{s}}}+1\right)-V_{T}\ln \left({\frac {v_{2}}{RI_{s}}}+1\right)\right]=V_{T}\ln \left[\left({\frac {v_{1}}{RI_{s}}}+1\right)\left({\frac {v_{2}}{RI_{s}}}+1\right)\right]

因此，最終輸出為

v_{b}=-RI_{s}\left(e^{\frac {v_{a}}{V_{T}}}-1\right)=-{\frac {v_{1}\cdot v_{2}}{RI_{s}}}-(v_{1}+v_{2})

很明顯，輸出結果中包含了我們想要的乘積，但也存在一個多餘的項。不能簡單地將其視為錯誤，因為它可能與乘積項一樣大，因此必須將其移除。不過，這是一個簡單的任務，只需要新增另一個階段，使其精確地求和 $v_{1}+v_{2}$ ，這樣就沒有誤差了。完整的乘法器電路如下：

其中輸出電壓由以下公式給出：

v_{out}=-\left(-{\frac {v_{1}\cdot v_{2}}{RI_{s}}}-(v_{1}+v_{2})+(v_{1}+v_{2})\right)={\frac {v_{1}\cdot v_{2}}{RI_{s}}}

這正是我們想要的。只要滿足以下關係，電路就可以正常工作：

v_{1},v_{2}>-RI_{s}

因此，輸入可以為零或略微負值，但由於 $RI_{s}$ 將是一個很小的電壓，因此可以簡單地將關係改寫為 $v_{1},v_{2}\geq 0$ 。從數學的角度來看，這是因為我們無法計算負數的對數；從物理的角度來看，這個限制是由於我們只能獲得極小的電流（幾乎為零）反向偏置二極體。

在實際應用中，二極體被替換為以二極體方式工作的 BJT。

MOS 實現

由於可以將 MOSFET 電晶體用作電壓控制電阻，因此可以利用此特性來建立模擬乘法器。參考右邊的圖片 - 字母表示不同的引腳：Drain（漏極）、Source（源極）和 Gate（柵極）。MOS 器件是對稱的，因此漏極和源極可以互換，不會影響器件的行為。使用 _源極_ 作為最低電壓端，使用 _漏極_ 作為最高電壓端。當柵極和漏極之間的電壓超過閾值電壓時，即 $V_{GD}>V_{TH}$ ，電流和電壓之間的關係如下：

I_{DS}=K[2(V_{GS}-V_{T})V_{DS}-V_{DS}^{2}]\simeq 2K(V_{GS}-V_{T})V_{DS};\qquad V_{GD}>>V_{TH}

假設我們始終可以使用這種關係，那麼模擬乘法器的配置如下：

其中兩個器件的源極和漏極都已標出。如果 $v_{2}$ 和 $V_{ref}$ 為正值，那麼由運算放大器，源極將處於虛擬接地。流過 $R_{1}$ 的電流很明顯：電阻的一端具有電壓 $v_{1}$ ，另一端處於（虛擬）接地。相同的電流將流過 MOS $M_{2}$ ，從而確定電壓 $V_{G}$ 。電流由以下公式給出：