電子學/節點分析
外觀
< 電子學
電子學 | 前言 | 基礎電子學 | 複雜電子學 | 電學 | 機器 | 電子學歷史 | 附錄 | 編輯
節點是電路中連線元器件的部分。根據基爾霍夫電流定律,進入節點的所有電流都必須離開節點。節點上的每個點都具有相同的電壓,無論它與每個元器件的距離多麼近,因為元器件之間的連線是完美的導體。這種電壓稱為節點電壓,是節點與任意參考點(接地點)之間的電壓差。接地點是一個定義為電壓為零的節點。應仔細選擇接地點以方便分析。請注意,接地點不一定表示與地面的實際連線,它只是一個使分析更簡單的工具。例如,如果一個節點的電壓為 5 伏,則該節點與接地點之間的電壓降將為 5 伏。
請注意,在實際電路中,節點由導線構成,這些導線不是完美的導體,因此電壓在節點上的每個位置都不完全相同。這種區別僅在要求苛刻的應用中很重要,例如低噪聲音訊、高速數位電路(如現代計算機)等。如果我們檢視特定電路的功能,工程師可能能夠選擇彼此相對的檢查點,這表示電流穿過另一個點的兩個點,這可能是測試電路以確定節點工作原理的另一種方法。
節點分析是基於KCL方程的形式化程式。
步驟
- 識別所有節點。
- 選擇一個參考節點。用參考(接地)符號識別它。一個好的選擇是具有最多分支的節點,或者一個可以立即為您提供另一個節點電壓的節點(例如,在電壓源下方)。
- 為其他節點分配電壓變數(這些是節點電壓)。
- 為每個節點編寫一個KCL方程(將離開節點的所有電流相加,並設定為零)。將這些方程重新排列成A*V1+B*V2=C的形式(或類似於具有更多電壓變數的方程)。
- 求解步驟 4 中的方程組。可以使用多種技術:簡單的代入法、克萊姆法則、伴隨矩陣法等。
- 受控電流源
- 解決方案:為每個節點編寫KVL方程。然後用節點電壓表示額外變數(電流源所依賴的任何變數)。重新排列成上面步驟 4 中的形式。如步驟 5 中所示求解。
- 獨立電壓源
- 問題:我們不知道電壓源的電流。我們無法為電壓源連線到的節點編寫KCL方程。
- 解決方案:如果電壓源位於參考節點和任何其他節點之間,則我們已經獲得了“免費”的節點電壓:節點電壓必須等於電壓源值!否則,使用“超級節點”,包括源及其連線的節點。為進入和離開超級節點的所有電流編寫KCL方程。現在我們有一個方程和兩個未知數(節點電壓)。另一個關聯這些電壓的方程是由電壓源提供的方程(V2-V1=源值)。此新的方程組可以如上所述在步驟 5 中求解。
- 受控電壓源
- 解決方案:與獨立電壓源相同,但多了一個步驟。首先編寫超級節點KCL方程。然後用節點電壓表示源控制量(依賴量?)。重新排列方程使其採用A*V1+B*V2=C的形式。如上所述求解方程組。
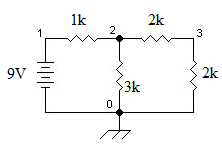
節點 0:(定義為接地點)
節點 1:(自由節點電壓)
節點 2:
節點 3:
得到以下線性方程組:
因此,解決方案為:
另一種使用KCL的解決方案是根據節點2求解節點電壓;