 NASA 蘭利研究中心的超音速噴氣發動機測試設施和測試,以評估噪聲排放
NASA 蘭利研究中心的超音速噴氣發動機測試設施和測試,以評估噪聲排放
預測氣動噪聲的一種直接方法是求解一般三維非定常可壓縮數值模擬中的 Navier-Stokes 方程。不幸的是,除了在有限區域內非常簡單的學術配置之外,這幾乎是無法實現的。聲學類比的想法是重新表述氣體動力學的完整方程,從遠處觀察者的角度提供均勻運動中均勻介質中的等效波動方程。此條件導致通常線性聲學問題[1] 的簡化。最系統地使用的形式主義是利希特爾的類比以及 Curle 和 Ffowcs Williams & Hawkings 所做的擴充套件,因為它們提供了廣泛的適用性。
必須明確說明的是,類比的目標不是本質上推匯出精確的結果或數值係數,而是從與經典波動方程相關的標準程式中推斷出一般規律。需要來自實驗、CFD 或分析方法的關於主要流動特徵的初步知識才能應用這些類比。此外,提取聲學結果的流動變數的精度程度對於確保預測方法的相關性至關重要。
參考文獻 [2] [3],下面的開發源於氣動聲學維基頁面。
 ..........................質量守恆方程 (E1)
..........................質量守恆方程 (E1)
其中  和
和  分別表示流體的密度和速度,它們依賴於空間和時間,而
分別表示流體的密度和速度,它們依賴於空間和時間,而  是實質導數。
是實質導數。
接下來是動量守恆方程,它由下式給出
 ..........................動量守恆方程 (E2)
..........................動量守恆方程 (E2)
其中  是熱力學壓力,而
是熱力學壓力,而  是來自 Navier–Stokes 方程的柯西應力張量的粘性(或無跡)部分。
是來自 Navier–Stokes 方程的柯西應力張量的粘性(或無跡)部分。
步驟 1: 將 (E1) 乘以  並將其加到 (E2) 中,得到
並將其加到 (E2) 中,得到

步驟 2: 對 (E1) 關於時間求導,對 (E2) 求散度,並將後者從前者中減去,得到

步驟 3: 從最後一個方程的兩邊減去 ,其中
,其中 是介質在其平衡(或靜止)狀態下的聲速,並重新整理,得到
是介質在其平衡(或靜止)狀態下的聲速,並重新整理,得到
![{\displaystyle {\frac {\partial ^{2}\rho }{\partial t^{2}}}-c_{0}^{2}\nabla ^{2}\rho =\nabla \cdot \left[\nabla \cdot (\rho \mathbf {v} \otimes \mathbf {v} )-\nabla \cdot \sigma +\nabla p-c_{0}^{2}\nabla \rho \right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/471371077cd60e5c6ef74c2df8a482bfb7f3f688)
它等價於
![{\displaystyle {\frac {\partial ^{2}\rho }{\partial t^{2}}}-c_{0}^{2}\nabla ^{2}\rho =(\nabla \otimes \nabla ):\left[\rho \mathbf {v} \otimes \mathbf {v} -\sigma +(p-c_{0}^{2}\rho )\mathbb {I} \right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/612e7b49b9ae21a4ad4361a54229226eaeeb7fdc)
其中 是單位張量,而
是單位張量,而 表示(雙重)張量收縮運算元。
表示(雙重)張量收縮運算元。
使用 _愛因斯坦記號_,Lighthill 方程可以寫成

其中  是所謂的 Lighthill 應力張量
是所謂的 Lighthill 應力張量  ,更多細節將在下一節提供。其中:
,更多細節將在下一節提供。其中: 是雷諾的慣性[check spelling] 應力張量
是雷諾的慣性[check spelling] 應力張量  是雷諾的粘性應力張量
是雷諾的粘性應力張量  代表所有由於熵非均勻性產生的影響(對於具有高溫度梯度的高溫射流很重要)
代表所有由於熵非均勻性產生的影響(對於具有高溫度梯度的高溫射流很重要)
航空聲學工程師需要在近似值的第一個步驟中預測渦輪發動機產生的噪聲,即傳播介質中區域性不穩定流。Lighthill (1952) 的基本思想是重新表述氣體動力學的一般方程,以推匯出波動方程。特徵變數是密度波動,因為它在氣體中的聲波是由壓縮性引起的。沒有進行特殊的假設,也沒有引入線性化。
 ...............................Lighthill 方程
...............................Lighthill 方程
其中 : 稱為 Lighthill 張量
稱為 Lighthill 張量
如果在等式兩邊加上相同的量,該方程仍然成立。加上 : ,其中
,其中  是未受擾動氣體的特徵聲速(準確地說,是流場周圍介質中的聲速,在應用中;這與流場中的區域性聲速
是未受擾動氣體的特徵聲速(準確地說,是流場周圍介質中的聲速,在應用中;這與流場中的區域性聲速  不同)。然後,在左側形成波動運算元,並將右側的所有其他項移除,得到
不同)。然後,在左側形成波動運算元,並將右側的所有其他項移除,得到
![{\displaystyle \ {\frac {\partial ^{2}\rho }{\partial t^{2}}}-c_{0}^{2}{\frac {\partial ^{2}\rho }{\partial x_{j}^{2}}}={\frac {\partial ^{2}}{\partial x_{i}\partial x_{j}}}[\rho V_{i}V_{j}+(P-c_{0}^{2}\rho )\delta _{ij}-\tau _{ij}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2ddb38c9610afcf63ea4e164ed29cc87681cb3b)
該結果是著名的 Lighthill 方程。當應用於聲學的實際問題時,由於右邊的所有項都可以忽略不計(根據與聲波傳播相關的合理假設,例如小振幅、等熵運動[4]),它簡化為遠離流動的均勻波動方程。Lighthill 方程的另一種形式可以用壓力而不是密度來表示,如下所示
 .....................*關於壓力波動的 LightHill 方程*
.....................*關於壓力波動的 LightHill 方程*
也許這個不太常見,因為密度波動與可壓縮效應直接相關,而壓力波動可以存在以補償流體中的慣性加速度。然而,當涉及溫度不均勻性時,壓力波動非常適合。
Lighthill 張量的每一項的解釋
聲學源可以分為三個不同的類別:
 單極聲源
單極聲源
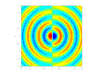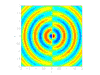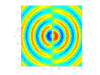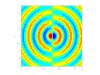
- 單極聲源:
 球形聲源或離散聲源,提供隨時間波動的流量
球形聲源或離散聲源,提供隨時間波動的流量  。只有在遇到固體表面時才會出現。
。只有在遇到固體表面時才會出現。
 偶極聲源
偶極聲源
- 偶極聲源:
 類似於兩個並排放置的單極聲源,它們具有相反的相位
類似於兩個並排放置的單極聲源,它們具有相反的相位  和
和  。偶極聲源與力
。偶極聲源與力  相關,根據我們結合的單極聲源所建立的軸線。與單極聲源一樣,它們只有在域中涉及固體表面時才會出現。
相關,根據我們結合的單極聲源所建立的軸線。與單極聲源一樣,它們只有在域中涉及固體表面時才會出現。
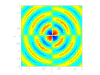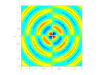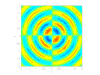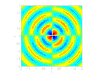 四極聲源
四極聲源
- 四極聲源:
 由兩個並排且相位相反的偶極聲源構成,這些聲源來自湍流渦旋,通常在低速流動中被忽略。它們起源於 Navier-Stokes 方程中的剪下項。
由兩個並排且相位相反的偶極聲源構成,這些聲源來自湍流渦旋,通常在低速流動中被忽略。它們起源於 Navier-Stokes 方程中的剪下項。
作為氣體動力學一般方程的推論,萊特希爾方程是精確的。所有氣動聲學過程,包括流動非均勻性產生的聲音,聲音在流動中的傳播以及粘度或熱傳導引起的聲能耗散,都被考慮在內。因此,由於等式右側包含待確定的聲場,並且不能被認為是真正的源項,所以該方程不能像使用線性聲學的純波方程那樣易於處理。因此,我們需要獨立於聲學變數來近似這個項,這對應於忽略某些機制。為了消除這個基本困難,萊特希爾提出了一些簡化,這些簡化是基於這樣的想法: **流體混合產生的聲音是主要的機制**,特別是在航空學中感興趣的高雷諾數情況下。這相當於優先考慮與流體慣性相關的機械效應,而將熱力學效應視為次要效應。
萊特希爾方程是適定方程,因為它假設源位於流動內部,而不是流動外部。在傳播區域,它簡化為齊次波方程。但是,為了在源附近求解,必須使用現象比較進行近似。
萊特希爾的類比經常被用於計算噴氣噪聲,在這種型別的應用中,我們有導致簡化的特定條件 [5]
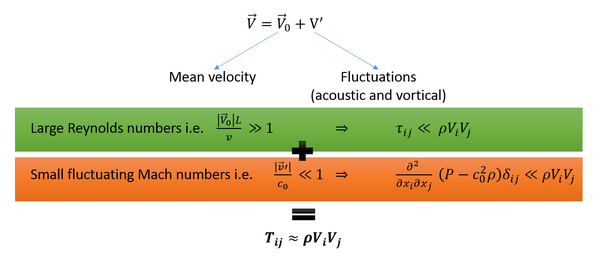
工業環境中使用的實際近似
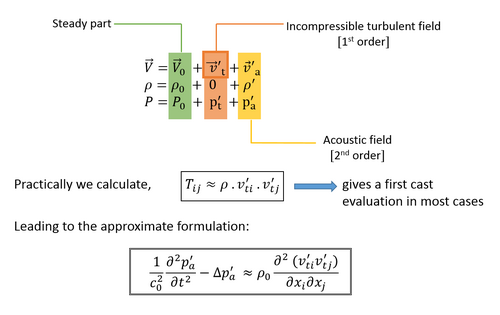
該近似使方程在某種意義上成為線性聲學中波方程的顯式方程,可以透過格林函式技術形式地求解。當使用數值方法來描述流動時,可以消除一些假設以進行更準確的評估,並將該方程用於後處理流動資料。
 偽聲現象的描述及其對近場和遠場假設以計算聲壓的影響
偽聲現象的描述及其對近場和遠場假設以計算聲壓的影響
如果熵非均勻性在擾動流中占主導地位,則源看起來像是等效的單極子
使用里布納分離和不可壓縮流體定律

得出最終的近似萊特希爾方程
 ..................... *近似萊特希爾方程*
..................... *近似萊特希爾方程*
1969年,弗勞克斯-威廉姆斯與霍金斯是第一批提出基本方程來預測流動中葉片產生的噪聲的科學家 [6]。
(存在幾種 FWH 類比的公式,這裡有一個適用於葉片噪聲描述現象的公式)
從萊特希爾方程推匯出來,它表明旋轉體中產生聲學源的波動壓力是特定非齊次波方程的解

其中,  是從源點到觀察點的向量座標,
是從源點到觀察點的向量座標,  是源域中的時間。
是源域中的時間。
源項  可以寫成以下求和形式
可以寫成以下求和形式

- 第一項
 代表由流體體積位移產生的 *厚度噪聲*。風扇葉片具有厚度和體積。當轉子旋轉時,每個葉片的體積會置換流體體積,從而導致附近區域的壓力波動,進而產生噪聲。這種噪聲在執行頻率處是調頻的,對於冷卻風扇來說通常很弱,因為它們的轉速相對較低。因此,風扇葉片的厚度幾乎不影響電子冷卻風扇的噪聲。(這種噪聲對於高速渦輪機械,例如直升機旋翼,可能變得很嚴重。)
代表由流體體積位移產生的 *厚度噪聲*。風扇葉片具有厚度和體積。當轉子旋轉時,每個葉片的體積會置換流體體積,從而導致附近區域的壓力波動,進而產生噪聲。這種噪聲在執行頻率處是調頻的,對於冷卻風扇來說通常很弱,因為它們的轉速相對較低。因此,風扇葉片的厚度幾乎不影響電子冷卻風扇的噪聲。(這種噪聲對於高速渦輪機械,例如直升機旋翼,可能變得很嚴重。)
- 第二項被稱為 *負載噪聲*,它來自於移動表面上力場
 的波動。在轉子中,它起源於流體和葉片之間的非定常氣動力。在計算模型中,該項由表面分佈的偶極子表示。(對於風扇來說占主導地位)
的波動。在轉子中,它起源於流體和葉片之間的非定常氣動力。在計算模型中,該項由表面分佈的偶極子表示。(對於風扇來說占主導地位)
- 最後一項是 *剪下噪聲*,它由葉片表面上的四極子組成 [7]。
Ffowcs Williams & Hawkings 理論允許在知道格林函式中的源項的情況下求解此方程。
在所有四極子項顯著且必須計算的應用中(優先發生在高速情況下),計算可能變得很繁瑣,因為源分佈在體積內部,其邊界沒有明確定義。相比之下,表面源項的計算要簡單得多,並且邊界清晰。如果 CFD 必須在圍繞表面的有限域中使用,並且如果計算能夠再現聲學近場,則可以透過在非區域性控制面(可以由使用者定義)而不是物理表面上獲取資訊,提出一種更方便的解決聲學問題的方法 [8]。可以應用雙層勢描述,在貝塞爾函式假設下求解亥姆霍茲方程。這種 Ffowcs Williams & Hawkings 類比的推廣形式在最近的計算聲氣動力學 (CAA) 中被廣泛使用。
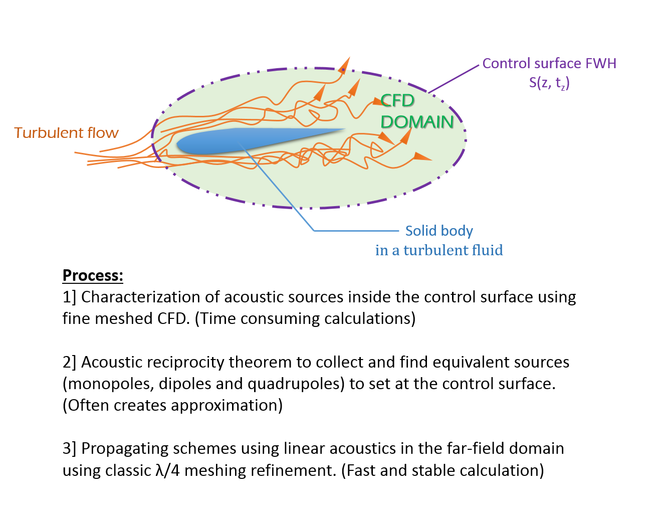 使用 FWH 類比和圍繞氣動外形的可滲透表面的聲氣動力學計算模擬
使用 FWH 類比和圍繞氣動外形的可滲透表面的聲氣動力學計算模擬
注意:控制面內的 CFD 域必須實現到生成的湍流系統完全發展為止(例如,使用 k- 準則)。
準則)。
類比的形式優勢是將聲氣動力學問題表述為一個典型的線性聲學問題,透過定義等效源,這些等效源將在均勻介質中產生與從流動和表面配置在觀察者位置聽到的相同聲音。初始氣體動力學方程的難度轉移到源項的描述中。形式解是使用線性聲學的理論基礎推匯出來的,但如果等效源項沒有在其他地方確定,它可能毫無用處。使用 Lighthill 和 FWH 類比允許工程師例如以更低的計算時間成本計算飛機發動機的噪聲。
美國宇航局和 CERFACS 機構正在進行密集的研究,試圖開發更有效的計算方案,以提供改進的設計工具,讓汽車工程師對噪聲預測充滿信心,併為下一代產品開發氣動機械聲學設計。
進行近似意味著丟棄預計可以忽略不計的現象,保留主要特徵。這僅僅是在提出一種解釋。
[1]Goldstein, M. E. (1976). 聲氣動力學。紐約,麥格勞 - 希爾國際圖書公司,1976 年。305 頁,1。
[2]Tam, C. K. (1995). 計算聲氣動力學 - 問題和方法。AIAA 雜誌,33(10), 1788-1796。
[3]Wang, M., Freund, J. B., & Lele, S. K. (2006). 流動產生的聲音的計算預測。流體力學年鑑,38, 483-512。
[4]Colonius, T., Lele, S. K., & Moin, P. (1993). 用於直接計算氣動聲學產生的邊界條件。AIAA 雜誌,31(9), 1574-1582。
[5] Williams, J. F. (1969). 流體動力噪聲。流體力學年度回顧,1(1), 197-222。
[6] Williams, J. F., & Hawkings, D. L. (1969). 湍流和任意運動表面產生的聲音。倫敦皇家學會哲學學報。A 系列,數學和物理科學,264(1151), 321-342。
[7] Ianniello, S. (1999). 透過 Ffowcs Williams-Hawkings 方程進行的四極子噪聲預測。AIAA 雜誌,37(9), 1048-1054。
[8]Di Francescantonio, P. (1997). 用於預測聲音輻射的一種新的邊界積分公式。聲學與振動雜誌,202(4), 491-509。


















![{\displaystyle {\frac {\partial ^{2}\rho }{\partial t^{2}}}-c_{0}^{2}\nabla ^{2}\rho =\nabla \cdot \left[\nabla \cdot (\rho \mathbf {v} \otimes \mathbf {v} )-\nabla \cdot \sigma +\nabla p-c_{0}^{2}\nabla \rho \right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/471371077cd60e5c6ef74c2df8a482bfb7f3f688)
![{\displaystyle {\frac {\partial ^{2}\rho }{\partial t^{2}}}-c_{0}^{2}\nabla ^{2}\rho =(\nabla \otimes \nabla ):\left[\rho \mathbf {v} \otimes \mathbf {v} -\sigma +(p-c_{0}^{2}\rho )\mathbb {I} \right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/612e7b49b9ae21a4ad4361a54229226eaeeb7fdc)













![{\displaystyle \ {\frac {\partial ^{2}\rho }{\partial t^{2}}}-c_{0}^{2}{\frac {\partial ^{2}\rho }{\partial x_{j}^{2}}}={\frac {\partial ^{2}}{\partial x_{i}\partial x_{j}}}[\rho V_{i}V_{j}+(P-c_{0}^{2}\rho )\delta _{ij}-\tau _{ij}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2ddb38c9610afcf63ea4e164ed29cc87681cb3b)



















