在機械波傳播的一般情況下,假設介質的強度性質可以用空間和時間的連續函式來描述。在壓力振幅變得非常大的極限情況下,波傳播會演變成波前變得不連續,必須用從波前未受擾動的熱力學狀態到波後最終熱力學狀態的跳躍來描述。
這種型別的傳播擾動,它產生壓力、溫度、焓、內能、密度和粒子速度的不連續變化,被稱為衝擊波。衝擊波在下圖中示意性地表示
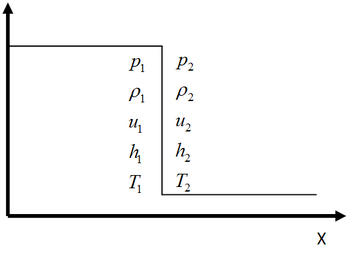
衝擊波最終可以被解釋為橫向機械波,其脈衝波長不可定義,以遠大於介質聲速的傳播速度不連續地改變介質的狀態。
考慮在彈性固體中衝擊波是如何形成的最直觀,因為這種行為原則上可以擴充套件到流體。對於線性彈性材料,壓縮載荷下的行為可以大致分為兩種情況。在彈性範圍內,變形(應變)與施加在其上的應力成正比。超過某個臨界應力水平(稱為屈服應力),應變不再與應力成正比,材料開始表現出非線性行為——這就是塑性範圍。
如果我們將材料中的聲速定義為

很明顯,在彈性範圍內,壓力和密度呈線性關係,因此如果波的壓力振幅低於材料的屈服應力,則傳播速度是恆定的。然而,考慮一個振幅處於材料屈服強度以上壓力的範圍內的波,如下圖所示

由於壓力振幅超過了應力和應變之間線性比例關係的範圍,因此波速不再恆定。透過查閱應力-應變曲線,可以明顯看出波速隨著超過彈性極限的壓力的增加而增加。因此,波形的C點將具有最低的區域性波速,而B點和A點將依次具有越來越高的波速。因此,波形中最高壓力部分的傳播速度快於低壓部分,最終將追趕上它們。該過程的時間推移如下圖所示

當平滑的波脈衝透過材料傳播時,瞬時速度較快的波部分會追趕上速度較慢的部分,脈衝本身會變得越來越陡峭,直到它呈現出與衝擊波相關的熟悉的、不連續的輪廓。因此,任何壓力振幅大於材料屈服強度的波最終都會“衝擊”並變得不連續,這是由於波速隨壓力的增加而呈非線性增加。
人們很容易認為,如果我們將衝擊波的演化在時間上進一步回放,垂直線的頂部將繼續超過底部,衝擊波前沿將變得傾斜。實際上,由於存在一個競爭性的波過程,它起到衰減衝擊的作用,因此這種情況不會發生。
一旦衝擊波在材料中形成,它就不能無限地傳播,除非它是由活塞機械驅動或在爆轟波中透過耦合化學反應自支撐。將表明,衝擊波的衰減和最終消散也是彈性極限以上壓力、密度和波速之間非線性關係的自然結果。
考慮以下方形脈衝衝擊波
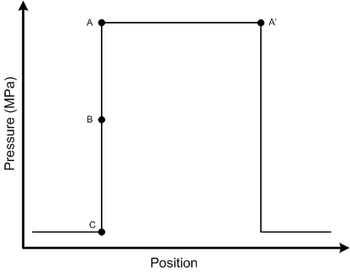
檢查點 A': 它正在以波速  運動到未受衝擊的材料中,相應的粒子速度為
運動到未受衝擊的材料中,相應的粒子速度為  。相比之下,點 A 正在以更高得多的壓力和密度運動到已經受衝擊的材料中,因此具有更高的粒子速度,
。相比之下,點 A 正在以更高得多的壓力和密度運動到已經受衝擊的材料中,因此具有更高的粒子速度, 和波速
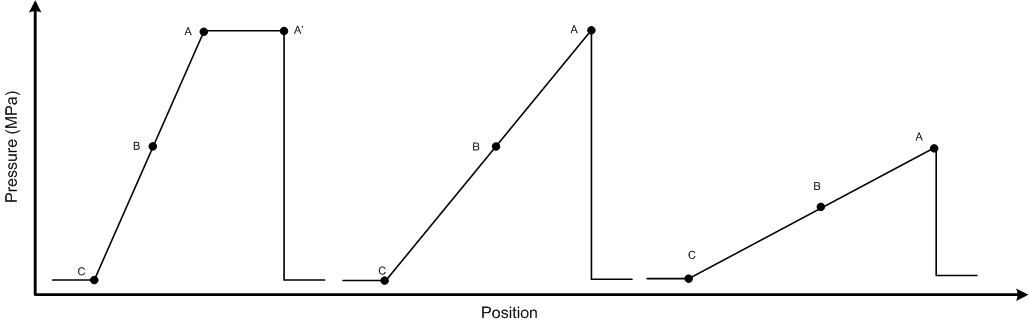
和波速  。因此,點 A 將比點 A' 運動得快得多,很快就會超過前沿。現在檢查點 C。它已被緩解到環境條件,因此具有較低的相關波速。因此,它將逐漸落後於點 A。當衝擊波傳播時,線 A-C 將伸長並因此向下傾斜。這可以看作衝擊脈衝幅度在越來越大的前沿厚度上的平均。這種平均作用會衰減脈衝,直到壓力衰減到彈性極限以下,衝擊波演變為聲波。實際上,線 A-C 是一種波過程,其傳播速度快於衝擊波前沿。這種波被稱為稀疏波,它是衝擊波過程的基本特徵。稀疏波衰減過程在下面的圖中描述。
。因此,點 A 將比點 A' 運動得快得多,很快就會超過前沿。現在檢查點 C。它已被緩解到環境條件,因此具有較低的相關波速。因此,它將逐漸落後於點 A。當衝擊波傳播時,線 A-C 將伸長並因此向下傾斜。這可以看作衝擊脈衝幅度在越來越大的前沿厚度上的平均。這種平均作用會衰減脈衝,直到壓力衰減到彈性極限以下,衝擊波演變為聲波。實際上,線 A-C 是一種波過程,其傳播速度快於衝擊波前沿。這種波被稱為稀疏波,它是衝擊波過程的基本特徵。稀疏波衰減過程在下面的圖中描述。
雖然之前的討論對於理解衝擊波的行為非常直觀,但所有這些結果都可以透過特徵線法和黎曼不變數對非線性波動方程的數學求解直接獲得。特徵線法是一種透過將偏微分方程簡化為常微分方程組來求解偏微分方程的技術,方法是對現有的座標系進行引數化,將其轉換為一個新的系統,在這個新系統中,偏微分方程的特性在新的系統中的曲線保持不變。在該方法中揭示的輪廓被稱為特徵線。
考慮一組基本的非線性彈性波動方程
 應變-密度關係
應變-密度關係
 本構方程
本構方程
 質量守恆
質量守恆
 動量守恆
動量守恆
和特徵座標


受約束條件,其中 


其中我們定義

請注意,我們在這裡實際上使用了波速作為壓力和密度的函式的表示式!
得出約束方程


將約束方程與微分  和
和  結合得到
結合得到
![{\displaystyle d\zeta ={\frac {\partial \zeta }{\partial x}}[dx-(\nu -C\epsilon )dt]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b79c5700b4e823e95741b53f0eb93da9a44733a)
![{\displaystyle d\xi ={\frac {\partial \xi }{\partial x}}[dx-(\nu +C\epsilon )dt]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3be449f364cb95f24970e911eb02959060a3056b)
然後這些方程得出新座標系等高線的斜率
 當
當 
 當
當 
現在,我們必須應用這些關係將波方程的表示式從  空間轉換為
空間轉換為  空間。對本構方程求時間導數,並代入特徵線的斜率得到
空間。對本構方程求時間導數,並代入特徵線的斜率得到


為了簡單起見,進行代換 
將代入質量守恆和動量守恆方程得到


這些可以組合起來,並透過偏導數鏈式法則展開求解得到


這些是在  和
和  空間中的特徵方程。
空間中的特徵方程。
為了求解特徵輪廓,我們必須從某個參考狀態積分到某個最終狀態,並參照不變數,因此


這兩個方程表示波系統的黎曼不變數。它們可以組合起來得到特徵方程,其中應力和粒子速度的組合不發生變化,如下所示


簡單波是特徵空間中波方程的解,其中一個不變數是常數。考慮一個非線性波,我們設定

這使得應力、應變、粒子速度和聲速僅成為 的函式。從之前推匯出的座標輪廓的斜率,我們得到
的函式。從之前推匯出的座標輪廓的斜率,我們得到

直接積分這些輪廓得到

因此,特徵空間中非線性方程的簡單波解可以描述為將一個指定的橫向運動脈衝轉換為一組具有不同斜率的直線特徵。每條線都可以解釋為脈衝上一個特定點的 x-t 歷史。
如果我們計算黎曼積分
![{\displaystyle \ \nu -\nu ^{0}={\frac {1}{2}}J_{+}\left[t-{\frac {x}{\nu +c}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/177fd3b17dbcd6b0a6e371711a819fb9f4f3d6e7)
![{\displaystyle \ \int _{1}^{\epsilon }{C(\epsilon )\,d\epsilon }=-{\frac {1}{2}}J_{+}\left[t-{\frac {x}{\nu +c}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1aad614ac7768a3f76134ef4bf47e3b9db62d121)
我們得到重要的結果

這個不等式從數學上證實了我們之前關於波速在非線性(塑性)狀態下隨壓力增加而增加的論述,並闡明瞭一個重要概念:波速等於粒子速度和聲速之和。
特徵空間中的簡單波解之間的關係可以透過以下概念與激波的形成聯絡起來:具有不同斜率的特徵最終會在某個時刻相交。
從數學上可以證明,非線性波輪廓的交點是一個數學上的間斷,從而驗證了我們關於激波是狀態間斷的概念。
為了簡便起見,考慮一個相對於位置是粒子速度斜坡的波 - 這類似於我們第一節中之前的定性示例,但用粒子速度繪製而不是壓力(兩者是相關的)。描述這個斜坡的方程是

應用我們對簡單波特徵的解,我們得到
![{\displaystyle \ \nu =m[(\nu +c)t-x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f4804fb204c5c06128bea30f30a51b9b0f7c213)
為了使此解易於處理,我們必須使用狀態方程來數學地聯絡波速和粒子速度。由於我們沒有指定所討論的材料,因此可以簡單地假設這種關係是線性的,因此

將此代入我們得到的關於速度的關係,得到

顯然,當  時,粒子速度的值是未定義的,簡單波解失效,我們形成了激波。但是,當
時,粒子速度的值是未定義的,簡單波解失效,我們形成了激波。但是,當  為負數時,
為負數時, 的值永遠不會趨於無窮大,我們有一個膨脹波。如果我們在 x-t 圖上繪製斜坡底部的一個點(對應於我們之前討論中的點 C)和斜坡頂部的另一個點(對應於點 A)的位置歷史,我們可以直觀地瞭解這些特徵是如何變化的。
的值永遠不會趨於無窮大,我們有一個膨脹波。如果我們在 x-t 圖上繪製斜坡底部的一個點(對應於我們之前討論中的點 C)和斜坡頂部的另一個點(對應於點 A)的位置歷史,我們可以直觀地瞭解這些特徵是如何變化的。

重要的是要注意,我們的數學和概念討論最終產生了關於激波形成和行為的類似描述。在數學討論中,我們可以看到每個特徵對應於  或
或  空間中描繪的波形的特定點的軌跡。這些特徵的歷史記錄了波形特定部分是如何超越或滯後於其他部分的。對於一組收斂的特徵,交點對應於數學奇點和激波的形成。對於發散的特徵,我們可以看到波形點開始在空間中擴散 - 這明顯類似於膨脹波的描述。
空間中描繪的波形的特定點的軌跡。這些特徵的歷史記錄了波形特定部分是如何超越或滯後於其他部分的。對於一組收斂的特徵,交點對應於數學奇點和激波的形成。對於發散的特徵,我們可以看到波形點開始在空間中擴散 - 這明顯類似於膨脹波的描述。
在特徵方法的背景下,激波是由特徵線的收斂產生的任何間斷。根據激波如何影響熱力學狀態軌跡,激波解分為兩種型別。弱激波定義為最終狀態和參考狀態之間的變化幾乎與等效的簡單特徵收斂波相同的情況。在這種情況下,導致狀態變化的過程是等熵的,材料從參考狀態載入到最終狀態的路徑由等熵線描述。
相反,強激波是所有可能狀態軌跡不與等熵線重合,而是遵循不同載入路徑的間斷解。
關於狀態軌跡的討論將在引入 Hugoniot 後變得更加清晰。
- 非線性流體和固體中波傳播導論;D.S. Drumheller;1998
- 炸藥工程;Paul W. Cooper;1996
- 激波和爆炸;P.L. Sachdev;2004


























![{\displaystyle d\zeta ={\frac {\partial \zeta }{\partial x}}[dx-(\nu -C\epsilon )dt]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b79c5700b4e823e95741b53f0eb93da9a44733a)
![{\displaystyle d\xi ={\frac {\partial \xi }{\partial x}}[dx-(\nu +C\epsilon )dt]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3be449f364cb95f24970e911eb02959060a3056b)






















![{\displaystyle \ \nu -\nu ^{0}={\frac {1}{2}}J_{+}\left[t-{\frac {x}{\nu +c}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/177fd3b17dbcd6b0a6e371711a819fb9f4f3d6e7)
![{\displaystyle \ \int _{1}^{\epsilon }{C(\epsilon )\,d\epsilon }=-{\frac {1}{2}}J_{+}\left[t-{\frac {x}{\nu +c}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1aad614ac7768a3f76134ef4bf47e3b9db62d121)


![{\displaystyle \ \nu =m[(\nu +c)t-x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f4804fb204c5c06128bea30f30a51b9b0f7c213)






