工程聲學/平面波的反射、透射和折射

二維平面波

二維平面壓力波可以用笛卡爾座標系描述，將波數分解為 x 和 y 分量，

$\mathbf {p} (x,y,t)=\mathbf {P} e^{j(\omega t-K_{x}x-K_{y}y)}.$

代入一般的波動方程得到

$\nabla ^{2}\mathbf {p} -{\frac {1}{c_{o}^{2}}}{\frac {\partial ^{2}\mathbf {p} }{\partial t^{2}}}=0,$

$\mathbf {P} (-K_{x}^{2}-K_{y}^{2})+{\frac {\omega ^{2}}{c_{o}^{2}}}\mathbf {P} =0,$

$K={\frac {\omega }{c_{o}}}={\sqrt {K_{x}^{2}+K_{y}^{2}}}.$

波數變成一個向量量，可以用方向餘弦表示，

${\vec {K}}=K_{x}{\boldsymbol {\hat {\imath }}}+K_{y}{\boldsymbol {\hat {\jmath }}}=K\cos(\alpha ){\boldsymbol {\hat {\imath }}}+K\cos(\beta ){\boldsymbol {\hat {\jmath }}}.$

斜入射平面波

考慮介質 1 中的斜入射平面波，它以 $\theta _{i}$ 角相對於法線入射到邊界。部分波以 $\theta _{r}$ 角反射回介質 1，其餘部分以 $\theta _{t}$ 角透射到介質 2。

$\mathbf {p_{1}} =\mathbf {P_{i}} e^{j(\omega t-\cos \theta _{i}K_{1}x-\sin \theta _{i}K_{1}y)}+\mathbf {P_{r}} e^{j(\omega t+\cos \theta _{r}K_{1}x-\sin \theta _{r}K_{1}y)}$

$\mathbf {p_{2}} =\mathbf {P_{t}} e^{j(\omega t-\cos \theta _{t}K_{2}x-\sin \theta _{t}K_{2}y)}$

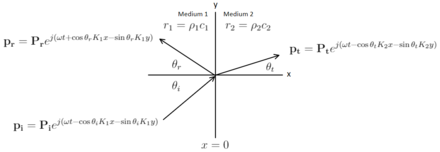斜入射平面波的反射和透射。

注意，波的頻率在邊界處不會改變，但特定聲阻抗從介質 1 改變到介質 2。傳播速度在每種介質中不同，因此波數在邊界處發生變化。需要滿足兩個邊界條件。

1. 聲壓在邊界處必須連續。
2. 垂直於邊界的粒子速度分量在邊界處必須連續。

施加第一個邊界條件得到

$\mathbf {p_{1}} (x=0)=\mathbf {p_{2}} (x=0),$

$\mathbf {P_{i}} e^{-j\sin \theta _{i}K_{1}y}+\mathbf {P_{r}} e^{-j\sin \theta _{r}K_{1}y}=\mathbf {P_{t}} e^{-j\sin \theta _{t}K_{2}y}.$

為了使連續性成立，指數必須全部相等

$K_{1}\sin \theta _{i}=K_{1}\sin \theta _{r}=K_{2}\sin \theta _{t}.$

這有兩個含義。首先，入射波的角度等於反射波的角度，

$\sin \theta _{i}=\sin \theta _{r}$

其次，斯涅爾定律被恢復，

${\frac {\sin \theta _{i}}{c_{1}}}={\frac {\sin \theta _{t}}{c_{2}}}.$

第一個邊界條件可以用聲壓反射和透射係數來表示

$1+\mathbf {R} =\mathbf {T} .$

施加第二個邊界條件得到

$\mathbf {u_{1x}} (x=0)=\mathbf {u_{2x}} (x=0),$

$\mathbf {u_{i}} \cos \theta _{i}+\mathbf {u_{r}} \cos \theta _{r}=\mathbf {u_{t}} \cos \theta _{t}.$

利用聲阻抗的定義，可得

${\frac {\mathbf {P_{i}} }{r_{1}}}\cos \theta _{i}-{\frac {\mathbf {P_{r}} }{r_{1}}}\cos \theta _{r}={\frac {\mathbf {P_{t}} }{r_{2}}}\cos \theta _{t}.$

利用反射係數、透射係數和聲阻抗比，可以得到

$1-\mathbf {R} ={\frac {\cos \theta _{t}}{\cos \theta _{i}}}{\frac {\mathbf {T} }{\zeta }}.$

求解壓力反射係數，可以得到

$\mathbf {R} =\mathbf {T} -1={\frac {{\frac {\cos \theta _{i}}{\cos \theta _{t}}}\zeta -1}{{\frac {\cos \theta _{i}}{\cos \theta _{t}}}\zeta +1}}={\frac {{\frac {r_{2}}{\cos \theta _{t}}}-{\frac {r_{1}}{\cos \theta _{i}}}}{{\frac {r_{2}}{\cos \theta _{t}}}+{\frac {r_{1}}{\cos \theta _{i}}}}}.$

求解壓力透射係數，可以得到

$\mathbf {T} =\mathbf {R} +1={\frac {2{\frac {\cos \theta _{i}}{\cos \theta _{t}}}\zeta }{{\frac {\cos \theta _{i}}{\cos \theta _{t}}}\zeta +1}}={\frac {2{\frac {r_{2}}{\cos \theta _{t}}}}{{\frac {r_{2}}{\cos \theta _{t}}}+{\frac {r_{1}}{\cos \theta _{i}}}}}.$

求解聲阻抗比，可以得到

$\zeta ={\frac {\cos \theta _{t}}{\cos \theta _{i}}}{\Big (}{\frac {1+\mathbf {R} }{1-\mathbf {R} }}{\Big )}={\frac {\cos \theta _{t}}{\cos \theta _{i}}}{\Big (}{\frac {\mathbf {T} }{2-\mathbf {T} }}{\Big )}.$

瑞利反射係數

瑞利反射係數將斯涅爾定律中的入射角與 $\mathbf {R}$、$\mathbf {T}$ 和 $\zeta$ 的方程式中的透射角聯絡起來。從三角恆等式，

$\cos ^{2}\theta _{t}+\sin ^{2}\theta _{t}=1$

並使用斯涅爾定律，

$\cos \theta _{t}={\sqrt {1-{\Big (}{\frac {c_{2}}{c_{1}}}\sin \theta _{i}{\Big )}^{2}}}.$

注意，為了使透射角為實數，

$c_{2}<{\frac {c_{1}}{\sin \theta _{i}}}$

必須滿足。因此，存在一個臨界入射角，使得

$\sin {\theta _{c}}={\frac {c_{1}}{c_{2}}}.$

瑞利反射係數代回 $\mathbf {R}$、$\mathbf {T}$ 和 $\zeta$ 的方程式，以獲得僅用阻抗和入射角表示的表示式。

$\mathbf {R} =={\frac {\cos \theta _{i}\zeta -{\sqrt {1-{\Big (}{\frac {c_{2}}{c_{1}}}\sin \theta _{i}{\Big )}^{2}}}}{\cos \theta _{i}\zeta +{\sqrt {1-{\Big (}{\frac {c_{2}}{c_{1}}}\sin \theta _{i}{\Big )}^{2}}}}}$

$\mathbf {T} ={\frac {2\cos \theta _{i}\zeta }{\cos \theta _{i}\zeta +{\sqrt {1-{\Big (}{\frac {c_{2}}{c_{1}}}\sin \theta _{i}{\Big )}^{2}}}}}$

$\zeta ={\frac {\sqrt {1-{\Big (}{\frac {c_{2}}{c_{1}}}\sin \theta _{i}{\Big )}^{2}}}{\cos \theta _{i}}}{\Big (}{\frac {1+\mathbf {R} }{1-\mathbf {R} }}{\Big )}={\frac {\sqrt {1-{\Big (}{\frac {c_{2}}{c_{1}}}\sin \theta _{i}{\Big )}^{2}}}{\cos \theta _{i}}}{\Big (}{\frac {\mathbf {T} }{2-\mathbf {T} }}{\Big )}.$