工程聲學/Rankine-Hugoniot 跳躍方程

守恆方程和推導

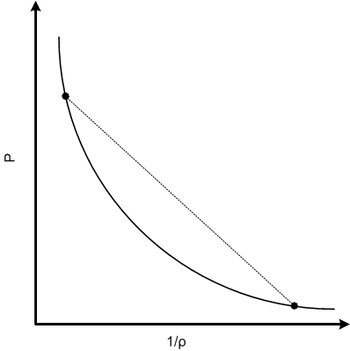
為了進行工程計算，需要將衝擊前後的狀態聯絡起來的方程。將狀態聯絡起來的兩個最基本的表示式之一是 $(P,\rho )$ Hugoniot 方程，它將壓力和密度關聯起來，

$\ P=f(\rho )$

此表示式可以透過簡化規範守恆方程來推匯出

質量守恆

$\rho _{1}\nu _{1}=\rho _{o}\nu _{o}\,$

動量守恆

$p_{1}+\rho _{1}\nu _{1}^{2}=p_{o}+\rho _{o}\nu _{o}^{2}$

能量守恆

$e_{1}+{\frac {p_{1}}{\rho _{1}}}+{\frac {1}{2}}\nu _{1}^{2}=e_{o}+{\frac {p_{o}}{\rho _{o}}}+{\frac {1}{2}}\nu _{o}^{2}$

完全求解跳躍條件所需的衝擊引數有壓力、粒子速度、比內能、密度和衝擊速度。有 4 個狀態變數，只有 3 個方程，因此需要一個額外的方程來關聯一些狀態，使問題易於處理。這個方程被稱為狀態方程 (EOS) - 存在許多 EOS 用於各種應用。最常見的 EOS 是理想氣體定律，它可以用來將方程組簡化為穩態流體中具有恆定比熱的 Hugoniot 表示式。

${\frac {p_{1}}{p_{2}}}={\frac {(\gamma +1)-(\gamma -1){\frac {\rho _{2}}{\rho _{1}}}}{(\gamma +1){\frac {\rho _{2}}{\rho _{1}}}-(\gamma -1)}}$

對於一般的非線性彈性材料，不存在可以從第一原理推匯出的狀態方程。然而，大量的實驗資料表明，幾乎所有材料都顯示出粒子速度和衝擊速度之間存線上性關係（特徵線方法示例中線性假設的準確性現在更加明確了！）。

$\ U=C_{o}+s\nu$

此方程也稱為 $U-\nu$ 平面上的衝擊 Hugoniot 方程。

將這種線性關係與動量和質量方程結合起來，可以得出幾乎所有固體材料的 $P-\rho$ 平面上的 Hugoniot 表示式。

$\ P=C_{o}^{2}{\frac {{\frac {1}{\rho _{0}}}-{\frac {1}{\rho }}}{\left({\frac {1}{\rho _{0}}}-{\frac {s}{\rho }}\right)^{2}}}$

路徑和躍變條件

Hugoniot 描述了材料在衝擊波後方可能存在的所有熱力學狀態的軌跡，這些軌跡投影到二維狀態-狀態平面上。因此，它是一組平衡狀態，並不專門代表材料發生轉變的路徑。

再次考慮我們對強衝擊和弱衝擊的討論。據稱弱衝擊是等熵的，並且等熵代表了材料透過具有會聚特性的等效波（稱為壓縮波）從初始狀態載入到最終狀態的路徑。在弱衝擊的情況下，Hugoniot 因此將直接落在等熵線上，並且可以直接用作等效路徑。

在強衝擊的情況下，我們不能再直接進行這種簡化，但是對於工程計算而言，等熵線足夠接近 Hugoniot，因此可以做出相同的假設。

如果 Hugoniot 近似於“等效”壓縮波狀態之間的載入路徑，則衝擊載入路徑的躍變條件可以透過在初始狀態和最終狀態之間畫一條直線來確定。這條線稱為瑞利線，方程如下

$\ P_{1}-P_{0}=U^{2}\left(\rho _{0}-{\frac {\rho _{0}^{2}}{\rho _{1}}}\right)$