享受數學 - 用有趣的數學謎題學習解決問題
| 一位華夏公益教科書人認為此頁面應該拆分為包含更窄子主題的更小頁面。 您可以透過將此大頁面拆分為更小的頁面來提供幫助。請確保遵循命名策略。將書籍分成更小的部分可以提供更多的焦點,並允許每個部分做好一件事,這有利於所有人。 |
簡介
這本書旨在作為 4-7 年級學生和老師的數學問題解決教科書。在美國,它旨在用於滿足美國數學教師全國委員會 (NCTM) 關於解決問題的標準,該標準總結如下。
從幼兒園到 12 年級的教學計劃應該使所有學生能夠——
- 透過解決問題來構建新的數學知識;
- 解決數學和其他環境中出現的問題;
- 應用和調整各種合適的策略來解決問題;
- 監控和反思數學問題解決的過程。
提高數學教育質量的一個關鍵挑戰是,在輕鬆獲得被認為是令人愉快的替代娛樂活動的情況下,激發學生對學習的興趣。休閒數學確定了包括成人和兒童都可以享受的謎題在內的數學活動。數獨謎題就是一個很好的例子。另一個例子是肯肯®謎題,紐約時報稱其為“自數獨以來最令人上癮的謎題”。目前,這類謎題在課堂上的作用非常有限,因為只有少量數學課程可以用這些謎題來教授。本書的目的是在有趣的數學謎題的背景下,為各種各樣的數學問題解決主題提供課程。謎題問題特別適合教創造性解決問題。謎題問題通常足夠難,需要應用各種問題解決策略。反思這個過程可以讓你進一步瞭解數學。
以下人員對本書做出了重大貢獻。如果您對本書做出了重大貢獻(即添加了重要的內容或進行了大量的編輯),請隨時在下面新增您自己的引用。
| 姓名 | 角色 | 評論 |
|---|---|---|
| Deepak Kulkarni | 作者/貢獻者 | 本書的初始版本包括我之前擁有版權的文字,我想在知識共享署名-相同方式共享 3.0 未本地化版本許可下發布這些文字。Deepak_S_Kulkarni (討論) 2012 年 11 月 7 日 (UTC) |
自古以來,人們就喜歡遊戲、魔術表演、比賽和謎題等活動。因此,發現學生喜歡基於數學的類似活動並不奇怪。有各種各樣的基於數學的遊戲和數學遊戲軟體。Krypto 和 24 是數學遊戲的很好的例子。和遊戲一樣,比賽對許多喜歡透過做一些事情來贏得一些東西的孩子來說也很有吸引力。因此,數學競賽可以成為孩子們喜歡並且可以鼓勵孩子們解決數學問題的活動。在參加比賽的過程中,有些孩子開始喜歡數學。在美國,學生可以參加的數學競賽包括 NOETIC 學習數學競賽、MOEMS、北南基金會的數學蜂、數學袋鼠、世界數學日、密西西比大學數學挑戰賽、線上數學聯盟、MATHCOUNTS 和 AMC。數學魔術技巧包括關於猜測數字和一些基於數學的紙牌技巧。
還有另一種娛樂活動是做數學謎題。本書將考察各種數學技巧在數學謎題中的應用。特別是,我們將研究肯肯這個謎題中的創造性問題解決。我們喜歡做謎題,因為我們有一種自然的傾向,會被驚喜、矛盾和知識的差距所驅動。雖然數學謎題可以激發和吸引學生,讓他們開始行動,但具有挑戰性、質疑和反思的氛圍可以使數學問題解決的體驗更加愉快。
有了正確的態度和練習,學生可以享受數學思維的過程。這個過程包括思考數學問題,觀察美麗的數學模式,提出優雅的見解,面對你可能能夠或不能解決的難題,體驗解決這些問題的興奮感,反思數學思維,並從成功和失敗中學習。一旦學生開始喜歡創造性的數學問題解決,他們就可以在任何地方享受這項活動。然後,創造性思維的樂趣就是他們激勵自己開始解決任何具有挑戰性的數學問題的動力。
對於一些問題,學生在讀題時就能夠知道應該使用什麼策略。然而,對於特別困難的問題,他們並不能立即知道該如何解決。解決這類問題的進展往往來自啟發式方法或“經驗法則”,這些方法可能有用,但不能保證能夠解決問題。因此,解決問題的過程往往需要進行多次探索,或嘗試不同的想法。解決問題的過程可能經歷不同的階段,例如嘗試理解問題,制定特定的方法,卡住並嘗試擺脫困境,批判性地檢查解決方案,或進行交流。這個過程可能涉及在這些不同的工作階段之間反覆進行。在這本書中,我們將提供各種不同的解決問題的經驗法則。這些啟發式方法可以用條件和相關行動的形式來描述,其中條件描述問題的情況,行動描述在這種情況下的應對措施。
情況:您即將開始解決一個問題嗎?您是否正在嘗試理解一個問題?
嘗試透過以下問題來理解問題
給定的是什麼?需要找到什麼?是否可以繪製問題描述的背景的圖片或圖表?您可以重新措辭問題嗎?您可以提出與問題相對應的具體例子嗎?
情況:您已經想出瞭解決問題的方案嗎?
如果解決問題的總體方法對您來說是顯而易見的,請根據此方法建立一個解決問題的計劃,並執行該計劃。
如果您知道一個相關或類似的問題,您可以使用相關問題解決方案的知識來制定計劃。
如果您無法制定解決問題的方案,您可能感到卡住了,您可能想要嘗試更好地理解問題。
情況:您是否感到卡住了?
可以嘗試許多不同的方法來擺脫困境。一種方法是嘗試解決問題的簡化版本,並使用問題的解決方案來獲得對解決原始問題有用的見解。
當您發現一個模式或“頓悟”時,請嘗試更詳細地研究引發它的觀察結果,並嘗試觀察它們如何在解決問題方面發揮作用。
或者,您也可以嘗試更好地理解問題並使用相關建議。
情況:您是否正在忙於解決細節?
監控您的進度,並在需要時回溯。
不要忘記尋找模式、異常和驚喜(頓悟)。
尋找任何驚喜;瞭解它及其對問題的意義。
情況:您是否已經完成解決問題或子問題,或推斷出關鍵結論?
批判性地檢查您的假設和解決方案。
已經完成解決問題了嗎?如果它起作用,請檢查每個步驟。您能清楚地看到該步驟是正確的嗎?您能證明它是正確的嗎?
從反思中學習:專門化/泛化啟發式方法。學習新的啟發式方法。如果計劃在短時間內沒有產生解決方案,那麼請不時檢查:您為什麼要做您正在做的事情?您是否正在取得進展?這是自我監控。如果您的計劃失敗了,請檢查它為什麼沒有奏效。用評分標準或模板書寫有助於回憶和研究您迄今為止所做的事情。組織資訊。問:關於無效的方法,您能得出什麼結論?您還學到了什麼?您是否看到任何模式?
情況:您即將向老師或合作伙伴傳達您的結論嗎?
解決問題的最後一步是傳達您的結論。傳達的內容可能因情況而異。有時,您只需要報告問題的答案。有時,您需要展示您的工作。有時,您可能正在進行協作性問題解決。在這種情況下,良好的溝通能力至關重要。幫助他人解決您已經解決的問題可以幫助您培養成為一名優秀的數學交流者的技能。這類交流的方面包括向他人清楚地解釋您的解決方案,理解他人的解決方案,並在不同細節層次上提供反饋。在為您的解決方案建立解釋之後,仔細檢查您是否已經證明了工作中的每個步驟。
具體的解決問題策略
1. 改變表示
使用錯誤的表示可能會使問題無法解決。改變表示的策略包括繪製圖片並從完全不同的角度看待問題。透過繪製圖片並使用它來視覺化有關問題的資訊,您將對問題有更清晰的理解,這將有助於您找到解決問題的方法,否則您可能看不到這些方法。
2. 制定一個有條理的清單或表格
制定一個有條理的清單可以讓您清楚地檢查資料。它可以幫助您確保您正在檢視所有相關資訊。它還將使您能夠輕鬆地看到資料中的模式並得出正確的結論。同樣,制定表格可以讓您清楚地檢查資料。它可以幫助您確保您正在檢視所有相關資訊。它還將使您能夠輕鬆地看到資料中的模式並得出正確的結論。
3. 建立一個更簡單的問題
有時,我們無法按原樣解決問題,但我們可以解決一個在某些方面類似的更簡單的問題。例如,類似的問題可能使用更簡單的數字。一旦我們解決了一個或多個更簡單的問題,我們可能就會理解可以用來解決類似型別問題的方案,並可能能夠解決我們被賦予的問題。
4. 使用邏輯推理
邏輯推理在數學問題中以各種方式發揮作用。它可以用來排除可能的選項。它有時也可以用來直接得出答案。
5. 猜測和檢查
“猜測和檢查”策略可以應用於許多問題。如果可能的答案數量很少,則可以使用此策略快速得出答案。在其他一些情況下,即使可能的答案數量不少,人們仍然可以進行明智的猜測並得出答案。
6. 逆向工作
有時,從問題的末尾開始,向問題的開頭反向工作,比從開頭開始向結尾工作更容易。
面對困難問題的正確態度
通常,當一個人無法解決問題時,就會感到沮喪。自然的傾向是感到失望,因為“自我”會受到傷害。在解決問題的早期階段,一個人可能在解決問題時卡住了。當您卡住時,您可能不知道可以採取什麼行動來解決問題。但是,您可能相信老師希望您做一些工作。因此,您對這種情況感到不快。此外,當您卡住並且無法想到前進的方法時,您會預料到您很可能無法解決問題。這增加了這種情況的沮喪情緒。這解釋了為什麼人們經常看到學生對難題持消極態度。
幫助學生享受工作和堅持努力的態度包括以下一些要素
- 接受過程:接受解決難題的過程,在這個過程中,您會長時間工作,而且您並不總是確定自己是否能夠解決問題,以及“卡住”是一種正常狀態,以及這種過程包括各種情緒。
- 接受挑戰的興奮:當一個人進行一項簡單的任務時,無法完成它被視為一件令人擔憂的事情,而完成它則不是一件大事。相反,當一個人進行一項具有挑戰性的任務時,無法完成它並不令人擔憂,因為這項任務本身對任何人都很困難。當一個人完成一項具有挑戰性的任務時,會有巨大的滿足感和成就感。儘管如此,當您卡住時感到沮喪是正常的。當這種情況發生時,您可以先嚐試確定問題的難點,並寫下有關卡住狀態的資訊。學習一些可以始終在您卡住並且不知道可以嘗試什麼方法時使用的方法(例如,嘗試一個更簡單的問題)。最初,將目標定為“嘗試在解決問題方面取得進展”,而不是將目標定為完全解決看似非常困難的問題。因此,在解決難題的過程中,人們會設定許多短期目標,並且即使人們沒有在總體目標上取得成功,也會在其中許多目標上取得成功。特別是,當您使用解決問題的簡化版本或解決問題的專門情況的策略時,請意識到您實際上是在解決過程中的某些問題,並取得了進展。取得進展包括收集資訊、注意到模式以及獲得關於問題的見解。這樣,即使您在解決問題並取得進展時沒有完全解決問題,您也會有一種成就感。有時,在最初感到沮喪之後,人們能夠在解決問題方面取得進展並解決問題。
- 對待失敗的態度:不要因失敗而氣餒。閱讀這位著名科學家愛迪生的名言。一位助手問道:“為什麼您要浪費時間和金錢?我們已經失敗了又失敗,幾乎失敗了一千次。您為什麼要繼續追求這項不可能的任務?”愛迪生說:“我們沒有失敗一千次,我們只是發現了用一千種方法無法發明電燈。”失敗往往比成功提供了更大的學習機會。
此外,對學習的渴望有一個明確的目標,即嘗試從解決問題過程中的成功和失敗中學習。為了學到最多,您需要反思成功和失敗。此外,如果您正在解決您並不總是能夠解決的問題,那麼您將學到最多。
- 欣賞數學之美:欣賞您在解決問題的過程中遇到的特別巧妙的見解和“頓悟”。這些可能是您在解決問題的過程中遇到的有趣的模式和驚喜。數學美包含在解決問題的過程中,對意想不到的事物感到驚訝,對未曾預料到的關係的感知以及困惑和啟發的交替出現。數學美體現在模式中。著名數學家哈代寫道:“數學家,就像畫家或詩人一樣,是模式的創造者。如果他們的模式比其他模式更持久,那是因為它們是用思想創造的。數學家的模式,就像畫家或詩人的模式一樣,必須是美麗的;思想,就像顏色或文字一樣,必須和諧地融合在一起。”
- 對數學交流的興趣:在解決問題的過程中,以及在反思成功和失敗時,將你所學到的見解寫下來很有幫助。與他人交流這兩個方面的見解也很有幫助。如果你在課堂上學到一個數學技巧或一個謎題,你可能想與你的朋友或兄弟姐妹分享。
關於問題解決的信念
學生往往對數學的本質抱有某些信念,這些信念阻礙了他們創造性地解決難題的能力。以下是一些誤導性信念的例子:
- 解決問題的方法並不唯一。
- 普通學生不可能理解數學。
- 數學問題總是由個人而不是由一群人解決的。
- 數學成績優異的學生能在很短的時間內解決任何問題。
- 學校學習的數學主題在現實生活中沒有用。
從反思中學習
練習得越多,你就會越好。但是,僅僅練習是不夠的。對問題解決經驗的反思可以幫助學生了解問題情況和問題解決過程。
回憶一下你是如何朝著解決方案前進的。記住進展過程中的重要方面。記住你卡住的階段以及你是如何恢復的。此外,還記得你遇到的“頓悟”時刻。
你能從你的經驗中學到什麼?是什麼讓這個問題變得困難?什麼有效?什麼無效?你學到了什麼教訓?它是否告訴你不同方法對這類問題的有效性?如果你表達了特定的經驗法則或策略,那麼這些策略有效的理由是什麼?在什麼情況下這些策略會奏效?這些是更普遍策略的特殊情況嗎?
反思問題解決經驗的一個重要部分是更好地理解在未來問題情況下有用的策略和經驗法則,並在可能的情況下,想出新的經驗法則。這包括更好地理解啟發式方法適用的情況,以及專門化或概括啟發式方法。
父母和朋友的影響
朋友和父母在幫助孩子們培養對數學的積極態度方面發揮著非常重要的作用。
孩子們經常會被激勵去參加學校的數學俱樂部,因為他們可以和朋友一起玩。如果俱樂部提供零食,那可能會提供額外的動力。數學俱樂部確實鼓勵對數學的積極態度,並有助於提高數學方面的成功水平。如果你有一個對數學有濃厚興趣的孩子,但班上沒有興趣相似的朋友,鼓勵他/她參加學校的數學俱樂部會很有幫助。其他選擇包括讓他/她參加GATE數學課程,在那裡他/她可以與興趣相似的孩子互動。夏季數學夏令營也能達到這個目的。
父母可以透過在家做數學和支援數學來鼓勵學生對數學產生興趣,從而發揮重要作用。
數學謎題
[edit | edit source]各種數學謎題
數學謎題是休閒數學的組成部分。它們有特定的規則,就像多人遊戲一樣,但通常不涉及兩個或多個玩家之間的競爭。相反,為了解開這樣的謎題,解題者必須找到一個滿足給定條件的解決方案。數學謎題需要數學來解開。邏輯謎題是一種常見的數學謎題。
康威的生命遊戲和分形,作為兩個例子,也可以被認為是數學謎題,即使解題者只在開始時透過提供一組初始條件與它們互動。設定這些條件後,謎題的規則決定所有後續的改變和移動。許多謎題之所以廣為人知,是因為馬丁·加德納在他的《科學美國人》雜誌上的“數學遊戲”專欄中討論過它們。數學謎題有時被用來激勵學生學習小學數學問題解決技巧。這個列表並不完整。
List of mathematical puzzles
以下類別並不互斥;有些謎題屬於多個類別。
數字、算術和代數
- 縱橫字謎或數字縱橫字謎
- 戴森數
- 四個四
- 數獨
- 費曼長除法謎題
- 海盜戰利品問題
- 文字算術
Combinatorial
- 密碼
- N-拼圖|十五拼圖
- 數獨
- 魔方和其他順序移動謎題
- Str8ts,一種基於序列的數字謎題
- 數獨
- 思考點
- 漢諾塔
Analytical or differential
- 橡膠繩上的螞蟻
- 另請參見:芝諾悖論
Probability
- 蒙提霍爾問題
Tiling, packing, and dissection
- 瘋人院立方體
- 康威謎題
- 殘缺棋盤問題
- 裝箱問題
- 五格骨牌鋪磚
- 斯洛陶伯-格拉茨馬謎題
- 索瑪立方體
- T形拼圖
- 七巧板
Involves a board
- 康威的生命遊戲
- 殘缺棋盤問題
- 單人跳棋
- 數獨
Chessboard tasks
- 八皇后問題
- 騎士巡遊
- 三子棋問題
Topology, knots, graph theory
結理論和拓撲學的領域,尤其是它們的反直覺結論,通常被視為休閒數學的一部分。
- 解開纏結謎題
- 哥尼斯堡七橋問題
- 水、煤氣和電
Mechanical
- 魔方
- 思考點
0-player puzzles
- 康威的生命遊戲
- 多面體
- 多格骨牌
在這本書中,我們將使用數獨和數獨的例子。所以,我們將詳細討論這些例子。
數獨
[edit | edit source]數獨是一種基於邏輯的組合數字放置謎題。目標是填充一個 9×9 的網格,用數字,使每一列、每一行以及組成網格的九個 3×3 子網格(也稱為“方塊”、“塊”、“區域”或“子方格”)包含從 1 到 9 的所有數字。謎題設定者提供一個部分完成的網格,通常只有一個解決方案。
完成的謎題始終是一種拉丁方,在單個區域的內容上有一個額外的約束。例如,同一個單一整數不能在同一個 9×9 的棋盤行或列中出現兩次,也不能在 9×9 棋盤的九個 3×3 子區域中的任何一箇中出現兩次。
這個謎題在 1986 年由日本謎題公司 Nikoli 在名為數獨的名字下推廣,意思是單個數字。
雖然 9×9 網格和 3×3 區域是最常見的,但存在許多變體。示例謎題可以是 4×4 網格,包含 2×2 區域;5×5 網格,包含五格骨牌區域,已在名為Logi-5的條件下發布;世界謎題錦標賽已展示了 6×6 網格,包含 2×3 區域,以及 7×7 網格,包含六個七格骨牌區域和一個不連續區域。更大的網格也是可能的。泰晤士報提供了一個 12×12 網格的Dodeka 數獨,包含 12 個 4×3 方格的區域。戴爾定期出版 16×16 的數字地點挑戰者謎題(16×16 變體通常使用 1 到 G 而不是十六進位制中使用的 0 到 F)。Nikoli 提供 25×25 的數獨巨人龐然大物。數獨zilla,一個 100×100 網格的謎題,於 2010 年在印刷品中出版。
另一個常見的變體是在通常的行、列和方塊要求之外,新增數字放置的限制。通常限制採用額外的“維度”的形式;最常見的是要求網格主對角線上的數字也唯一。前面提到的數字地點挑戰者謎題都是這種變體,就像每日郵報中的數獨 X 謎題一樣,它們使用 6×6 網格。iPhone/iPad 應用的數獨 X4 系列將這種“X”變體與星期日電訊報風格的相互交錯的彩色九格骨牌或拼圖|拼圖形狀的九個空格結合在一起,而不是 3x3 區域,提供總共四種不同的謎題。
迷你數獨在美國報紙《今日美國》和其他地方出現了一個名為“迷你數獨”的變體,它是在 6×6 網格上進行的,包含 3×2 區域。目標與標準數獨相同,但謎題只使用 1 到 6 的數字。類似的形式,用於解決更年輕的謎題解決者的謎題,稱為“少年數獨”,已在一些報紙上出現,例如《每日郵報》的某些版本。
交叉和數獨另一個變體是在 9×9 網格上將數獨與數獨結合起來,稱為交叉和數獨,其中線索以交叉和的形式給出。線索也可以透過神秘的文字算術給出,其中每個字母代表 0 到 9 之間的單個數字。例如,NUMBER+NUMBER=KAKURO 有一個唯一的解決方案 186925+186925=373850。另一個例子是SUDOKU=IS×FUNNY,其解決方案是 426972=34×12558。
殺手數獨
殺手數獨變體結合了數獨和數獨的元素。
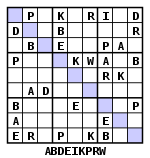
字母數獨
出現了字母變化,有時被稱為Wordoku;除非字母拼出單詞,否則謎題在功能上沒有任何區別。一些變體,例如在TV Guide中,包括一個單詞,一旦解開,就會沿著主對角線、行或列讀出;提前確定單詞可以被視為解題輔助。Wordoku可能包含其他單詞,而不是主單詞。
超級數獨
超級數獨是最流行的變體之一。它由世界各地的報紙和雜誌出版,也被稱為“NRC Handelsblad|NRC Sudoku”、“Windoku”、“Hyper-Sudoku”和“4 Square Sudoku”。佈局與普通數獨相同,但有額外的內部區域定義,其中必須出現數字 1 到 9。由於對重疊正方形的利用,解題演算法與普通數獨謎題略有不同。這種重疊為玩家提供了更多資訊,可以邏輯地減少剩餘正方形中的可能性。玩遊戲的策略與數獨相似,但可能更強調掃描正方形和重疊,而不是列和行。
由多個數獨網格構成的謎題很常見。五個 9×9 網格在角落區域以五星形圖案重疊,在日本被稱為 Gattai 5(五個合併)數獨。在The Times、The Age 和The Sydney Morning Herald中,這種形式的謎題被稱為Samurai SuDoku。Baltimore Sun 和Toronto Star 在週日版中出版了這種變體的謎題(標題為High Five)。通常,在重疊區域中找不到任何給定的值。順序網格,而不是重疊,也出版了,網格中特定位置的值需要轉移到其他網格中。
Str8ts 具有數獨在行和列中唯一性的要求,但第三個約束條件非常不同。Str8ts 使用黑色單元格(一些帶有線索數字)將棋盤分成隔間。這些必須用一組數字填充,這些數字形成一個“直線”,就像撲克牌中的順子一樣。順子是一組沒有間隙的數字,例如“4,3,6,5”——並且順序可以是非連續的。9×9 是傳統的尺寸,但透過適當放置黑色單元格,任何尺寸的棋盤都是可能的。
[[File:Comparison Sudoku.png|thumb|250px|數獨的示例 數獨的桌面版本可以使用標準的 81 張牌 Set 牌組(見 Set 遊戲)。三維數獨謎題由 Dion Church 發明,並於 2005 年 5 月在Daily Telegraph上發表。The Times 還以 Tredoku 的名稱釋出了三維版本。有一個數獨版本的魔方,叫做數獨魔方。
還有許多其他變體。一些是重疊 9×9 網格排列的不同形狀,例如蝴蝶、風車或花朵。其他則改變了用於解決網格的邏輯。其中之一是大於數獨。在這種情況下,數獨的 3×3 網格用 12 個大於符號(>)或小於符號(<)在兩個相鄰數字的公共線上給出。解決方案邏輯的另一個變體是無提示數獨,其中九個 9×9 數獨網格本身被放置在一個三乘三的陣列中。所有九個謎題中每個 3×3 網格的中心單元格都留空,並形成一個沒有完成任何單元格的第十個數獨謎題;因此,稱為“無提示”。
雙數獨
雙數獨是數獨的雙人變體。它在一個 4X4 的棋盤上進行,即 16 個方格或四個包含四個方格的叢集。
遊戲按照數獨的規則進行。使用四個數字,每個玩家依次放置四個數字中的一個,使自己不會犯任何非法動作。第一個犯非法動作的玩家輸掉。
KenKen 和 KenDoku 是 2004 年由日本數學教師宮本哲也發明的算術和邏輯謎題風格的商標名稱,他是一位創新者,他說他練習“不用教的教學藝術”。那些沒有使用 KenKen 或 KenDoku 商標權利的人有時會使用Calcudoku 和Mathdoku 這些名稱。
與數獨一樣,每個謎題的目標都是用數字填充一個網格——對於 4×4 網格,使用 1 到 4,對於 5×5 網格,使用 1 到 5,依此類推——這樣,每個數字在任何行或列中都不會出現超過一次(拉丁方格)。網格大小從 3×3 到 9×9 不等。此外,KenKen 網格被分成帶有重疊輪廓的單元格組——通常稱為“籠子”——並且每個籠子中的單元格中的數字必須使用指定的數學運算(加法、減法、乘法或除法)組合起來產生一個特定的“目標”數字。例如,在一個 4×4 謎題中,指定加法運算且目標數字為 6 的三個單元格籠子可以用數字 1、2 和 3 來滿足。數字可以在籠子內重複,只要它們不在同一行或列中即可。對於單個單元格籠子,沒有運算與之相關:在單元格中放置“目標”是唯一的可能性(因此成為一個“空位”。目標數字和運算出現在籠子的左上角。
示例


目標是用數字 1 到 6 填充網格,使得
- 每行都恰好包含一個數字
- 每列都恰好包含一個數字
- 每個用粗體輪廓線劃出的單元格組都是一個籠子,其中包含使用指定的數學運算(加法 (+)、減法 (-)、乘法 (×) 和除法 (÷))來實現指定結果的數字。(與殺手數獨不同,數字可以在籠子內重複。)
數獨和殺手數獨中的一些技巧可以在這裡使用,但大部分過程涉及列出所有可能的選項,並根據其他資訊逐一消除選項。
在本例中
- 最左側列中的“11+”只能是“5,6”。
- 頂行中的“2÷”必須是“1,2”、“2,4”或“3,6”之一。
- 頂行中的“20×”必須是“4,5”。
- 右上角的“6×”必須是“1,1,2,3”。因此,兩個“1”必須在不同的列中,因此第 1 行第 5 列是“1”。
- 第四行中的“30x”必須包含“5,6”。
- 左側的“240×”是“6,5,4,2”或“3,5,4,4”之一。無論哪種方式,五都必須在右上角的單元格中,因為我們已經在第 1 列中有了“5,6”,並且在第 4 行中也有“5,6”。
- 等等。
擴充套件 更復雜的 KenKen 問題是使用上述原則構建的,但省略了 +、-、× 和 ÷ 符號,因此將它們作為另一個未知數來確定。
在上一節中,我們描述了人們喜歡玩的一種謎題。在本節中,我們將討論與這些謎題的解題相關的各種數學概念。這些探索中的許多可以應用於多個謎題,但這裡將使用一個具體的例子進行討論,並會指出其他相關的謎題。由於學生可能喜歡某個特定的謎題,或者老師可能出於實際考慮選擇使用某個謎題,他們可能想研究這裡的探索,並在具體謎題的背景下練習這些探索。本書的目的是讓最廣泛的學生受益,這些學生對謎題充滿興趣。
相關謎題:數獨、數獨變體、KenKen
一個集合是事物的集合。例如,你穿的物品就是一個集合:這些物品包括裙子、襪子、帽子、襯衫、牛仔褲等等。你可以用大括號這樣寫集合:{裙子、鞋子、牛仔褲、手錶、襯衫,……}
兩個集合的並集是包含在兩個集合中的元素的集合。例如:設 A = {1, 2, 3} 且設 B = {3, 4, 5}。A 和 B 的並集寫成 A U B = {1, 2, 3, 4, 5}。不需要將 3 列出兩次。
兩個集合的交集是包含在兩個集合中的元素的集合。例如:設 A = {1, 2, 3} 且設 B = {3, 4, 5}。A 和 B 的交集寫成 A Ç B = {3}。有時根本沒有交集。在這種情況下,我們說答案是空集或空集。例如,給定集合 A = 所有大於 5 的素數,集合 B = 所有偶數素數,那麼 A 和 B 的交集 = {}。
A 和 B 之間的差集是指在 A 中但不在 B 中的元素。
A = {1, 2, 3} B = {3, 4} 那麼,A – B = {1, 2}
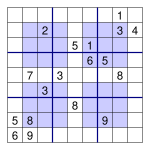
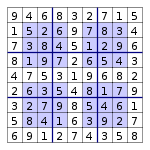
現在,考慮這裡顯示的數獨謎題。
考慮以下集合
S1 = 未在第二行分配的數字的集合。
S2 = 未在第二列分配的數字的集合。
S3 = 與 3x3 左上角網格約束一致的數字的集合。
S4 = 在第二行分配的數字的集合。
S5 = 在第二列分配的數字的集合。
練習
- 識別 S1、S2、S3、S4 和 S5。
- 找出 S1 和 S2 的交集。
- 找出 S1、S2 和 S3 的交集。
- 從你的 (3) 的答案中,你關於第二行第二格的結論是什麼?
- 在一個圖片中表示 S1、S2 和 S3。
- 找出 S4 和 S5 的並集。
- 有三個集合 F、R 和 C。三個集合的並集有 60 個成員。F 有 32 個成員。R 有 32 個成員。C 有 22 個成員。F 和 C 的交集有 10 個成員。有 10 個成員專門屬於 C。有 16 個成員專門屬於 R。有 6 個成員屬於 F、R 和 C 的交集。F 中有多少成員是專門屬於 F 的?
- 檢查上面顯示的數獨謎題。
識別以下集合。
S1:第 1 列中未分配的值的集合
S2:第 3 行中未分配的值的集合
找出 S1 和 S2 的交集。用它來確定第 1 列第 3 格中的可能值。
- . 上面的拼圖中,第九行第一列的方格中可以填入哪些數字?
- S1 有 10 個成員。S2 有 8 個成員。它們的並集有 16 個成員。它們的交集有多少成員?
- S1 有 30 個成員。S2 有 28 個成員。它們的並集有 46 個成員。它們的交集有多少成員?
- S1 有 100 個成員。S2 有 108 個成員。它們的並集有 200 個成員。它們的交集有多少成員?
- S1 有 100 個成員。S2 有 128 個成員。它們的並集有 128 個成員。它們的交集有多少成員?
- 在下面的表格中尋找規律。
S1 中的成員 |
S2 中的成員 |
交集中的成員 |
並集中的成員 |
8 |
8 |
4 |
12 |
8 |
8 |
3 |
13 |
8 |
8 |
2 |
14 |
8 |
9 |
4 |
13 |
8 |
10 |
4 |
14 |
8 |
11 |
4 |
15 |
9 |
11 |
5 |
15 |
- 反思你在這次探索中所學到的東西。寫下你學到的一些東西。
答案
- S1 = {2, 3,4,7,8} S2 = {1,2,4,5,7,8} S3 = {1, 2, 4,7} S4 = {1, 5,6,9} S5 = {3,6,9}.
- S1 和 S2 的交集 = {2,4,7,8}。
- S1、S2 和 S3 的交集 = {2,4,7}。
- 那個方格可以填 2、4 或 7。
- 留給讀者解答
- 留給讀者解答
- 用類似下面的表格或文氏圖來表示資訊。答案是,有 14 個成員只屬於 F。
僅 F |
僅 R |
僅 C |
F, R, 不屬於 C |
F, C 不屬於 R |
C, R 不屬於 F |
F, R, C | ||
16 |
10 |
6 | ||||||
60 |
全部 |
Y |
Y |
Y |
Y |
Y |
Y |
Y |
32 |
F |
Y |
Y |
Y |
Y | |||
32 |
R |
Y |
Y |
Y |
Y | |||
22 |
C |
Y |
Y |
Y |
Y | |||
10 |
F, C |
Y |
Y |
- 留給讀者。
- 留給讀者。
- 2
- 12
- 8
- 100
- 表格中有很多不同的規律。其中一個規律是,S1 中的元素數量 + S2 中的元素數量 = 交集中的元素數量 + 並集中的元素數量。
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 | |
A |
5040x |
18+ |
|||||||
確定上面 5040x 這樣的肯肯乘積籠中填入的數字,需要判斷目標數字是否可以被某個特定的因子整除。可除性規則在做這件事的時候特別有用。在本節探索中,我們將學習可除性概念。
練習
1) 可以被 5 整除的數字舉例如下:5, 10, 15, 20, 15, 20, 105, 110, 205, 2300。你發現這些數字有什麼規律嗎?
2) 你發現下面表格中列出的可以被 9 整除的數字有什麼規律嗎?
|
數字 |
27 |
927 |
9000 |
9909 |
20,007 |
17,127 |
900,009 |
|
各位數字之和 of digits |
9 |
18 |
9 |
27 |
9 |
18 |
18 |
3) 你發現下面表格中列出的可以被 6 整除的數字有什麼規律嗎?
|
數字 |
222 |
1002 |
7008 |
2004 |
220,026 |
|
各位數字之和 of digits |
6 |
3 |
15 |
6 |
12 |
|
末位數字 digit |
2 |
2 |
8 |
4 |
6 |
4) 你發現下面表格中列出的可以被 11 整除的數字有什麼規律嗎?
|
數字 |
22 |
1331 |
123,244 |
5060 |
7260 |
奇數位數字之和 |
2 |
4 |
8 |
0 |
2 |
偶數位數字之和 |
2 |
4 |
8 |
11 |
13 |
5) 你有 1 到 11 的數字,但不一定按順序排列。前九個數字的乘積是 441,760。最後兩個數字的和是 19。最後兩個數字是什麼?
6) 肯肯拼圖中的乘積籠的目標數字分別為 35、80、99、96 和 100。其中哪些數字可以被 5 整除?哪些數字可以被 6 整除?哪些數字可以被 9 整除?哪些數字可以被 11 整除?
7) 以下數字可以被 11 整除:A343, B15060, C22701, D030。A、B、C 和 D 分別是多少?
8) 2313E 可以被 6 整除。E 是多少?
9) 如果一個數字的末三位組成的數字可以被 8 整除,則該數字可以被 8 整除。以下哪些數字可以被 8 整除:(a)12,001, (b) 24,007, (c) 11,022, (d) 456,008, (e) 456,012.
10) 如果將一個數字的末位數字乘以 2,然後從該數字的其餘部分減去,結果為 0 或可以被 7 整除,則該數字可以被 7 整除。利用這個規則判斷以下哪些數字可以被 7 整除:(a)842, (b) 231, (c) 7078.
11) 反思你在這次探索中所學到的東西。寫下你學到的一些東西。
答案
1) 可以被 5 整除的數字的末位數字是 5 或 0。
2) 各位數字之和是 9 的倍數。
3) 各位數字之和是 3 的倍數,且末位數字為偶數。
4) 偶數位數字之和與奇數位數字之和的差是 11 的倍數或 0。
5) 觀察最後兩個數字的和為 19,我們可以得出結論,11 + 8 和 10 + 9 這兩種可能性都會得到 19 的和。我們知道其餘數字的乘積是 441,760。讓我們看看 11 是否是 441,760 的因子。
顯然,我們可以嘗試用 11 除 441,760。但是,有一個更簡單的方法來判斷 11 是否是 441760 的因子。這涉及使用一個叫做“11 的可除性規則”的規則。
從第一個數字開始,將所有隔一個數字的數字加起來得到 Sum_odd。然後,將剩下的數字加起來得到 Sum_even。求 Sum_odd 和 Sum_even 之差(Sum_odd - Sum_even 或 Sum_even - Sum_odd)。如果差值為 0 或 11 的倍數,則原始數字可以被 11 整除。
讓我們計算 Sum_odd 和 Sum_even,看看441,760是否可以被 11 整除。
我們得到 Sum_odd = 4 + 1 + 6 = 11 和 Sum_even = 4 + 7 + 0 = 11。
因此,Sum_odd - Sum_even = 0。因此,441,760可以被 11 整除。如果 11 在前 9 個數字中,那麼它一定不在最後兩個數字中。正如我們之前討論的那樣,最後兩個數字的唯一兩種可能性是 (11, 8) 或 (10, 9)。因此,我們可以得出結論,這兩個方格中的數字是 9 和 10。
所以,判斷一個數字是否可以被 11 整除的步驟如下:
1. 將奇數位數字加起來。
2. 將偶數位數字加起來。
3. 從兩個數字之和中較大的那個數字中減去較小的那個數字。如果你得到的數字可以被 11 整除,那麼原始數字也可以被 11 整除。
6) 35、80 和 100 可以被 5 整除。96 可以被 6 整除。99 可以被 9 整除。99 可以被 11 整除。
7) A343 可以被 11 整除。因此,(A + 4) 和 3 + 3 = 6 之差是 11 的倍數。如果 A + 4 = 6,則 A = 2。用類似的推理,我們發現 B 是 1,C 是 8,D 是 8。
8) 2313E 可以被 6 整除。因此,E 是偶數。此外,由於各位數字之和必須可以被 3 整除,所以 9 + E 可以被 3 整除。因此,E 必須是 3、6 或 9。由於 E 是偶數,所以 E 必須是 6。
9) 只有 456,008 可以被 8 整除。
10) 只有 231 可以被 7 整除。
關於肯肯乘積籠的推理涉及一組數字的乘法和除法。學習一些讓我們能夠快速進行乘法的技巧很有用。
練習
1) 你在下面的表格中觀察到什麼規律?
數字 |
乘積 |
2, 3, 5 |
30 |
2, 4, 5 |
40 |
2, 21 ,5 |
210 |
2, 28, 5 |
280 |
2, 18, 5 |
180 |
現在,根據你觀察到的規律,嘗試以下乘法。
2) 2 x 3 x 4 x 5
3) 2 x 3 x 4 x 5 x 6
4) 2 x 3 x 5 x 6
5) 2 x 2 x 3 x 5 x 5
6) 你在下面的表格中觀察到什麼規律?
數字 |
乘積 |
4, 3, 25 |
300 |
4, 4, 25 |
400 |
4, 21, 25 |
2100 |
4, 28, 25 |
2800 |
4, 18, 25 |
1800 |
答案
1) 為了尋找規律,觀察每一行中的條目之間的相似之處,以及不同列之間的相似之處。我們觀察到,乘積等於中間數字後面加一個 0。一般來說,如果我們有一個包含 2 和 5 的一系列數字的乘積,則執行以下操作:(a)將 2 和 5 替換為 10,(b)將剩餘的數字相乘,(c)將乘積乘以 10。
因為用 10 乘法可以透過在數字末尾新增一個零來輕鬆完成,所以這種重新排序使我們能夠更快地進行乘法。
2) 120
3) 720
4) 180
5) 300
6) 為了尋找規律,觀察每一行中的條目之間的相似之處,以及不同列之間的相似之處。我們觀察到,乘積等於中間數字後面加兩個 0。一般來說,如果我們有一個包含 4 和 25 的一系列數字的乘積,則執行以下操作:(a)將 4 和 25 替換為 100,(b)將剩餘的數字相乘,(c)將乘積乘以 100。因為用 100 乘法可以透過在數字末尾新增兩個零來輕鬆完成,所以這種重新排序使我們能夠更快地進行乘法。
以下是關於乘法技巧的更多探索
- 取幾個偶數,比較以下結果
- 用 5 乘以後得到的乘積
- 將該數字除以 2,然後乘以 10 所得到的結果。
將你的結果整理成一個列表。結果相同嗎?為什麼?哪種方法更容易獲得答案?
- 取幾個可以被 4 整除的數字,比較以下結果
- 用 25 乘以後得到的乘積
- 將該數字除以 4,然後乘以 100 所得到的結果。
將你的結果整理成一個列表。結果相同嗎?為什麼?哪種方法更容易獲得答案?
- 取幾個數字,比較以下結果
- 用 9 乘以後得到的乘積
- 將該數字乘以 10,然後減去原始數字所得到的結果。
將你的結果整理成一個列表。結果相同嗎?為什麼?哪種方法更容易獲得答案?
- 取幾個數字,比較以下結果
- 用 15 乘以後得到的乘積
- 將該數字除以 2,然後將該數字乘以 30 所得到的結果。
將你的結果整理成一個列表。結果相同嗎?為什麼?哪種方法更容易獲得答案?
- 反思你在這次探索中所學到的東西。寫下你學到的一些東西。
確定一個有兩個方格的籠子中填入的數字,需要找到一對因子,它們的乘積是給定的目標值。
尋找給定數字因子的步驟如下:
- 從 1 開始,用 1 到拼圖中允許的最大數字之間的每個數字除以給定數字。
- 如果數字能夠除盡,且沒有餘數,那麼你找到了一對因子。
- 將你的除法中的除數和商列為一對因子。
- 繼續除法,直到因子對重複。
練習
1) 找到 12 的因子對。
2) 找到 20 的因子對。
3) 找到 25 的因子對。
4) 找到 36 的因子對。
5) 找到 49 的因子對。
6) 找到 50 的因子對。
7) 找到小於 100 且因子數量為奇數的數字。
8) 反思你在這次探索中所學到的東西。寫下你學到的一些東西。
答案
1)
|
數字 |
除法 |
因子對 |
|
1 |
12 / 1 = 12 |
1, 12 |
|
2 |
12 / 2 = 6 |
2, 6 |
|
3 |
12 / 3 = 4 |
3, 4 |
|
4 |
12 / 4 = 3 |
重複的因子對 |
12 的因子對是 (1, 12), (2, 6) 和 (3, 4)。
2)
|
數字 |
除法 |
因子對 |
|
1 |
20 / 1 = 20 |
1, 20 |
|
2 |
20 / 2 = 10 |
2, 10 |
|
3 |
不能被整除 |
|
|
4 |
20 / 4 = 5 |
4, 5 |
|
5 |
20 / 5 = 4 |
重複的因子對 |
20 的因子對是 (1, 20), (2, 10) 和 (4, 5)。
3) 25 的因子對是 (1, 25) 和 (5, 5)。
4) 36 的因子對是 (1, 36), (2, 18), (3, 12), (4, 9) 和 (6, 6)。
5) 49 的因子對是 (1, 49) 和 (7, 7)。
6) 50 的因子對是 (1, 50), (2, 25) 和 (5, 10)。
7) 嘗試 1 到 10 之間的數字。我們發現有奇數個因子的數字是 1、4 和 9。尋找規律。這些是平方數。這是因為平方數有一個因子對,其中兩個數字相同,而其他因子對則有兩個不同的數字。小於 100 且有奇數個因子的數字是 1、4、9、16、25、36、49、64 和 81。
尋找因子三元組的步驟
- 首先,找到給定數字的所有因子對。
- 現在,對於每個因子對,找到第二個因子的因子對。用相應的因子對替換該因子。
- 刪除任何重複的因子三元組。
例如
對於 12,我們有以下因子對 (1) 1, 12 (2) 2, 6 (3) 3, 4
當我們用它的因子對替換 12 時,我們將得到
1, 1, 12
1, 2, 6
1, 3, 4
當我們用它的因子對替換 6 時,我們將得到
2, 1, 6
2, 2, 3
當我們用它的因子對替換 4 時,我們將得到
3, 1, 4
3, 2, 2
我們刪除重複項,得到
1, 1, 12
1, 2, 6
1, 3, 4
2, 2, 3
練習
1) 找到 15、45 和 36 的所有因子。
為了確保你找到了所有的因子,知道一個數字有多少個因子會很有用。
2) 1 的因子數為 1。10 的因子數為 4。100 的因子數為 9。1000 的因子數為 16。識別模式。10,000 有多少個因子?
3) 找到 15 的所有因子對和因子三元組。
4) 找到 12、16 和 18 的所有因子三元組。
解答
1) 15 的因子是 1、3、5 和 15。45 的因子是 1、5、3、15、9 和 45。36 的因子是 1、2、4、3、6、12、9、18 和 36。
2)
10,000 has 25 factors.
3) 15 的因子對和因子三元組是 (1, 15)、(3, 5)、(1, 1, 15)、(1, 3, 5)
4) 12 的因子三元組是 (1, 1, 12)、(1, 2, 6)、(1, 3, 4)、(2, 2, 3)
16 的因子三元組是 (1, 2, 8)、(1, 1, 16)、(1, 4, 4)、(2, 2, 4)
18 的因子三元組是 (1, 1, 18)、(1, 2, 9)、(1, 3, 6)、(2, 3, 3)
相關謎題:殺手數獨、肯肯
讓我們考慮以下 3x3 肯肯謎題。
A1 A2 A3
B1 B2 B3
C1 C2 C3
提示
A1 * B1 = 6
A2 和 A3 之差為 1
C1 和 C2 之差為 1
B2 + B3 + C3 = 7
找出 A1、A2、A3、B1、B2、B3、C1、C2 和 C3 是什麼。
可以這樣推理這個謎題。數字 2 和 3 將是唯一可以放在 6x 中的數字。左下角必須有 1,因為 2 和 3 在同一列的 6x 格中。中間下面的方塊必須是 2,因為它在目標為 1- 的格中,而左下角的方塊是 1。右下角必須是 3,因為左下角的方塊是 1,而中間下面的方塊是 2。由於右下角的方塊是 3,因此 7+ 格中的剩餘方塊必須加起來等於 4。因此,7+ 格中的中間行中間和右邊的方塊必須是 3 和 1。由於 1、2 和 3 必須在中間行,因此中間行的左邊的方塊必須是 2。現在,我們可以得出結論,頂行的左、中和右方塊必須是 3、1 和 2。
回顧和反思解決方案通常有助於獲得關於問題解決方法的進一步見解。在上述問題中,一開始就知道 6x 格有 2 和 3 是有幫助的,即使我們不知道順序。通常,識別出有唯一解的格是有用的。我們將在本章中進一步探討這一點。
現在,考慮以下問題
20x20 肯肯謎題中哪些有兩個方塊的目標和的格具有唯一解?
雖然你可能能夠想到一個或兩個這樣的格,但要確保所有這樣的格都比較難。一般來說,如果我們有一個難題,進行探索並從探索中獲得見解是有用的。在這裡,我們將考慮以下問題,它是一個更簡單的版本。
4x4 肯肯謎題中哪些有兩個方塊的目標和的格具有唯一解?
這裡一個好的策略是建立一個可能的兩個方塊格的表格。
要建立表格,請執行以下操作
- 識別相關數量。
- 理解這些數量之間的關係。
- 理解結果與這些數量之間的關係。
- 理解這些數量可以取的可能值,並建立這些值的排序列表。
- 從一個數量的第一個值開始,透過從低到高改變其他數量的值,建立所有與該數量對應的行。
- 一旦你完成了建立所有與該行的可能值對應的行,考慮該數量的下一個可能值,並建立相應的行。繼續直到你完成所有該數量的可能值的考慮。
- 對於表格中的每一行,計算結果。
練習
- 建立一個表格,列出兩個不同數字的所有可能和,其中每個數字可以是 1、2、3 或 4。表格的第一列應為較小的數字,第二列應為較大的數字。
- 在該表格中,識別出只有一對數字才能相加得到目標和的和。
- 建立一個表格,列出兩個不同數字的所有可能和,其中每個數字可以是 1、2、3、4 或 5。表格的第一列應為較大的數字,第二列應為較小的數字。
- 在您在先前問題中建立的表格中,識別出只有一對數字才能相加得到目標和的和。
- 建立一個表格,列出兩個不同數字的所有可能和,其中每個數字可以是 1、2、3、4、5 或 6。表格的第一列應為較大的數字,第二列應為較小的數字。
- 在您在先前問題中建立的表格中,識別出只有一對數字才能相加得到目標和的和。
- 建立一個表格,列出兩個不同數字的所有可能和,其中每個數字可以是 1、2、3、4、5、6 或 7。表格的第一列應為較大的數字,第二列應為較小的數字。
- 在您在先前問題中建立的表格中,識別出只有一對數字才能相加得到目標和的和。
- 識別以下表格中的模式。
謎題尺寸 |
具有唯一解的兩個方塊目標 |
4x4 |
2, 3, 6, 7 |
5x5 |
2, 3, 8, 9 |
6x6 |
2, 3, 10, 11 |
7x7 |
2, 3, 12, 13 |
- 10x10 肯肯謎題中有哪些兩個方塊目標和的格具有唯一解?
- 11x11 肯肯謎題中有哪些兩個方塊目標和的格具有唯一解?
- 12x12 肯肯謎題中有哪些兩個方塊目標和的格具有唯一解?
- 13x13 肯肯謎題中有哪些兩個方塊目標和的格具有唯一解?
- 14x14 肯肯謎題中有哪些兩個方塊目標和的格具有唯一解?
- 檢查 5x5、6x6 和 7x7 肯肯謎題中三個方塊的行列格的目標和。哪些格具有唯一解?
- 你能識別出與肯肯謎題尺寸和具有唯一解的目標和之間的模式嗎?
- 你能識別出 12x12 肯肯謎題中三個方塊的行列格的目標和,這些目標和具有唯一解嗎?
現在,考慮以下所示的三個方塊的 L 形謎題,讓我們研究目標和具有唯一解的格。在這個格中,頂行的 (1, 2) 和底部的 3 被視為不同於頂行的 (1, 3) 和底部的 2。
18) 4x4 肯肯謎題中 L 形三個格的目標和中哪些具有唯一解?
19) 5x5 肯肯謎題中 L 形三個格的目標和中哪些具有唯一解?
20) 6x6 肯肯謎題中 L 形三個格的目標和中哪些具有唯一解?
21) 7x7 肯肯謎題中 L 形三個格的目標和中哪些具有唯一解?
22) 你可以在以下表格中識別出哪些模式,該表格列出了三個方塊的 L 形格的目標和,這些目標和具有唯一解?
|
謎題尺寸 |
具有唯一解的目標 solutions |
|
4x4 |
4, 5, 10, 11 |
|
5x5 |
4, 5, 13, 14 |
|
6x6 |
4, 5, 16, 17 |
|
7x7 |
4, 5, 19, 20 |
23) 找出 12x12 和 13x13 肯肯謎題中三個方塊的 L 形格的目標和,這些目標和具有唯一解。
24) 識別以下具有唯一解的乘積目標中的模式:3、5、7、11、13。
25) 建立一個可能的數字表格,以確定 4x4 肯肯謎題中具有唯一解的減號目標數字。
26) 建立一個可能的數字表格,以確定 5x5 肯肯謎題中具有唯一解的減號目標數字。
27) 建立一個可能的數字表格,以確定 6x6 肯肯謎題中具有唯一解的減號目標數字。
28) 你能識別出與肯肯謎題尺寸和謎題中具有唯一解的減號目標之間的模式嗎?
29) 建立一個可能的數字表格,以確定 4x4 肯肯謎題中具有唯一解的兩個方塊格的除號目標數字。
30) 建立一個包含所有可能數字的表格,用於確定 5x5 肯肯遊戲中,保證唯一解的除法目標數字。
31) 建立一個包含所有可能數字的表格,用於確定 6x6 肯肯遊戲中,保證唯一解的除法目標數字。
32) 你能發現肯肯謎題的大小和保證唯一解的謎題中的除法目標數字之間的關係嗎?
33) 在以下表格中,列出了具有唯一解的乘積目標和相關的謎題大小,你能看到哪些模式?
大小 |
乘積 目標 |
3 |
2, 3 |
4 |
2, 3 |
5 |
2, 3, 5 |
6 |
2, 3, 5 |
7 |
2, 3, 5, 7 |
11 |
2, 3, 5, 7, 11 |
14 |
3, 5, 7, 11, 13 |
34) 在以下表格中識別出保證唯一解的乘積目標之間的模式。
|
大小 |
乘積 Targets with Unique Solutions
|
|
3 |
6 |
|
4 |
6 |
|
5 |
6,10, 15 |
|
6 |
6, 10, 15 |
|
12 |
15, 21, 22, 26, 33, 35, 55, and 77 |
解答
1) 讓我們使用本章中描述的步驟來建立一個表格。我們的兩列可以是兩個數字中較小的那個和較大的那個。我們知道我們要關注的結果是這些數量的總和。這些數字可以取的可能值是 1、2、3 和 4。列表為 [1, 2, 3, 4]。我們可以從較小的數字為 1 開始,並考慮以下可能性:(1, 2)、(1, 3) 和 (1, 4)。然後,我們可以考慮較小的數字為 2 的可能性。這裡,我們將考慮 (2, 3) 和 (2, 4) 的可能性。最後,我們將較小的數字設為 3,並計算總和為 7。現在,我們計算每一行中數量的總和。
|
較小 Number |
較大的數字 |
各位數字之和 |
1 |
2 |
3 |
1 |
3 |
4 |
1 |
4 |
5 |
2 |
3 |
5 |
2 |
4 |
6 |
3 |
4 |
7 |
2) 檢查 4x4 肯肯的表格,我們可以發現 3+、4+、6+ 和 7+ 是唯一與一個數字對相關聯的目標。
3) 留給學生建立表格。
4) 檢查 5x5 肯肯的表格,我們可以發現 3+、4+、8+ 和 9+ 是唯一與一個數字對相關聯的目標。
5) 留給學生建立表格。
6) 檢查 6x6 肯肯的表格,我們可以發現 3+、4+、10+ 和 11+ 是唯一與一個數字對相關聯的目標。
7) 留給學生建立表格。
8) 檢查 7x7 肯肯的表格,我們可以發現 3+、4+、12+ 和 13+ 是唯一與一個數字對相關聯的目標。
9) 讓我們檢查以下表格中的模式。
|
謎題 size |
兩個方格目標 有 unique solutions |
4x4 |
3, 4, 6, 7 |
5x5 |
3 ,4, 8, 9 |
6x6 |
3, 4,10, 11 |
7x7 |
3, 4, 12, 13 |
你在這裡的數字中看到模式了嗎?尋找模式的一種策略是檢視連續行之間有什麼共同點。首先,3 和 4 對於所有這些都是通用的。現在,讓我們檢查這些行中最大的目標數字:7、9、11、13。
在尋找模式時,另一種策略是尋找差異。
這裡連續數字之間的差異結果是 2。啊哈!因此,這些數字都增加了 2。有兩種模式:連續數字之間的模式和兩列條目之間的模式。兩種型別數量之間另一種可能的模式是,一種是另一種數量的倍數。在這裡,我們可以嘗試將第一列中的數字加倍,我們發現結果接近第二列中我們擁有的數字,但少了一個。我們注意到
7 = 2 * 4 - 1 (* 表示“乘以”。)
9 = 2* 5 - 1.
11 = 2 * 6 -1.
13 = 2 * 7 -1.
我們可以將此概括為以下假設
我們只能建立一個數字對,可以在 n * n 肯肯謎題中建立一個 2 * n - 1 的總和。
通常,用更多示例驗證給定假設是一個好主意。在這裡,如果我們可以檢查 8x8 和 9x9 肯肯謎題中的總和,我們會發現這個假設確實成立。
現在,讓我們檢查導致最大可能唯一總和的數字對。
|
謎題 size |
最大 sum target with unique solution and associated numbers |
|
4x4 |
7 = 3 + 4 |
|
5x5 |
9 = 4 + 5 |
|
6x6 |
11 = 5 + 6 |
|
7x7 |
13 = 6 + 7 |
觀察連續行之間的差異,我們會發現數字從一行到下一行增加了 1。此外,對於 n * n 肯肯謎題,這些數字是 n 和 n - 1。現在,讓我們看看是否可以建立一個邏輯解釋,說明為什麼目標 2n - 1 將有一個唯一的解決方案。如果兩個數字中的一個是小於 (n - 1) 的,那麼另一個數字必須大於 n 才能使總和為 2n - 1。但是,我們不能在總和中使用大於 n 的數字。因此,我們不能使其中一個數字小於 (n - 1)。此外,我們不能使用大於 n 的數字。因此,我們唯一可以用來建立 2n - 1 總和的數字是 n 和 n -1。
類似地,可以注意到,在我們迄今為止識別的第二大目標數字之間存在一個模式
|
謎題尺寸 |
第二大 target with unique solution
|
4x4 |
6 |
5x5 |
8 |
6x6 |
10 |
7x7 |
12 |
你能在這裡識別出模式嗎?你能對觀察到的模式提供一個邏輯解釋嗎?
同樣,在尋找模式時,一種可能的策略是尋找差異。這裡連續數字之間的差異結果是 2。因此,這些數字都增加了 2。我們注意到的另一個模式是
7 = 2 * 4 - 2.
9 = 2* 5 - 2.
11 = 2 * 6 - 2.
13 = 2 * 7 - 2.
我們在這裡的觀察結果如下
我們只能建立一個數字對,可以在 n * n 肯肯謎題中建立一個 2 * n - 2 的總和。總的來說,具有唯一解的 n * n 肯肯謎題的目標總和是 3、4、2n - 2 和 2n -1。
10) 3、4、18、19 是 10 x 10 肯肯謎題中的目標總和,這些謎題有唯一解。
11) 3、4、20、21 是 11 x 11 肯肯謎題中的目標總和,這些謎題有唯一解。
12) 3、4、22、23 是 12 x 12 肯肯謎題中的目標總和,這些謎題有唯一解。
13) 3、4、24、25 是 13 x 13 肯肯謎題中的目標總和,這些謎題有唯一解。
14) 3、4、26、27 是 14 x 14 肯肯謎題中的目標總和,這些謎題有唯一解。
15) 在 5x5 肯肯中,具有唯一總和的三個方格線性行籠的目標是 6、7、11 和 12。在 6x6 肯肯中,目標是 6、7、14 和 15。在 7x7 肯肯中,目標是 6、7、17 和 18。
16) 模式:唯一的目標總和是 6、7 以及 3n - 4 和 3n - 3。
17) 具有唯一總和的 12x12 肯肯中的目標是 6、7、32 和 33。
18) 4, 5, 10, 11
19) 4, 5, 13, 14
20) 4, 5, 16, 17
21) 4, 5, 19, 20
22) 具有三個方格 T 目標 4、5 以及 3n - 1、3n - 2 的 n x n 肯肯謎題將具有唯一解。
23) 4、5、34、35 是在 12x12 肯肯中具有唯一解的三個方格 T 籠的目標總和。4、5、37、38 是在 13x13 肯肯中具有唯一解的三個方格 T 籠的目標總和。
24) 這些是質數。
25) 在 4x4 肯肯中,目標是 3。
26) 在 5x5 肯肯中,目標是 4。
27) 在 6x6 肯肯中,目標是 5。
28) 在 n x n 肯肯中,目標是 n - 1。
29) 4 和 3 是 4x4 肯肯中保證唯一解的除法目標數字。
30) 5、4 和 3 是 5x5 肯肯中保證唯一解的除法目標數字。
31) 6、5 和 4 是 6x6 肯肯中保證唯一解的除法目標數字。
32) 對於 n x n 肯肯謎題,所有大於 n/2 且小於或等於 n 的數字都是保證唯一解的除法目標數字。
33) 第二列都是小於肯肯謎題大小的質數。
34) 這些數字大於任何籠子中允許的最大數字,並且這些數字是兩個質數的乘積。
相關謎題:數獨、數獨變種、肯肯
給定一個情況,可以使用邏輯推理來識別以下內容:什麼必須為真?什麼必須為假?什麼可能為真也可能為假?
現在,考慮以下問題
三個方格行籠是下面所示的籠子。
6x6 肯肯謎題中的一個三個方格行籠的目標是 13+。你能說出籠子中必須有哪個數字,以及哪些數字一定不在籠子裡嗎?
這裡,數字 2、3、4 和 5 可能在那裡也可能不在那裡。例如
6 + 4 + 3 = 12.
6 + 5 + 2 = 12.
我們有一個目標總和的示例,其中 5 是籠子中的一個數字,我們還有一個目標總和的示例,其中 5 不是籠子中的一個數字。因此,5 可能在那裡也可能不在那裡。現在,我們將討論一種可能的方法,該方法允許我們得出結論,即某些數字必須在那裡,或者某些數字一定不在那裡。
反證法示例 1
我們聲稱 6 一定在那裡。
為了證明這一點,我們將展示如果我們假設 6 不在那裡會發生什麼。
如果 6 不在那裡,三個數字可能的最大總和是 5 + 4 + 3 = 12。
但是,目標總和大於 12。
因此,我們遇到了一個不可能的情況。
我們假設的必須是假的。
因此,6 一定在那裡。
反證法示例 2
我們聲稱 1 一定不在那裡。
為了證明這一點,我們將展示如果我們假設 1 在那裡會發生什麼。
如果 1 在那裡,剩餘數字中最大的數字將是 6 和 5。然後,三個數字可能的最大總和是 6 + 5 + 1 = 12。
但是,目標大於 12。
因此,我們遇到了一個不可能的情況。
我們假設的必須是假的。
因此,1 一定不在那裡。
反證法的通用步驟
我們要證明 X 為真。
為了證明這一點,我們將展示如果我們假設 X 不為真會發生什麼。
如果 X 不為真,邏輯推理會導致不可能的情況。
因此,我們假設的必須是錯誤的。
因此,X 必須為真。
這種推理方法稱為“反證法”。
練習
考慮以下挑戰問題
我們在 12 x 12 的數獨中有一個五格的橫排籠子,目標總和為 17。我們可以對籠子中可能的數字得出什麼結論?哪些數字必須存在?哪些數字必須不存在?
我們將進行探索性研究以瞭解這類問題,以便我們能夠在這個問題上取得進展。
1) 對於 6x6 數獨中一個三格的橫排籠子,目標總和為 6 到 15,你能對可能的數字說些什麼?
2) 對於 20x20 數獨中一個三格的橫排籠子,目標總和為 8,最大的可能數字是多少?
3) 對於 20x20 數獨中一個三格的橫排籠子,目標總和為 49,最小的可能數字是多少?
4) 對於 11x11 數獨中一個四格的橫排籠子,目標總和為 35,最小的可能數字是多少?
5) 對於 20x20 數獨中一個四格的橫排籠子,目標總和為 11,最大的可能數字是多少?
6) 在 12x12 的數獨中,對於目標總和為:6、7、8、9、10、29、30、31、32、33 的三格橫排籠子,你能對可能的數字說些什麼?哪些數字必須存在?哪些數字不能存在?哪些數字可能存在?
7) 識別下表中的模式。
|
數字 allowed |
使用三個不同的數字 可能的最大總和 |
|
1, 2, 3, 4 |
9 |
|
1, 2, 3, 4, 5 |
12 |
|
1, 2, 3, 4, 5, 6 |
15 |
|
1, 2, 3, 4, 5, 6, 7 |
18 |
|
1, 2, 3, 4, 5, 6, 7, 8 |
21 |
8) 如果你可以使用 1 到 100 的任何數字,你能說出使用三個不同的數字的可能的最大總和是多少嗎?
9) 識別下表中的模式。
|
數字 allowed |
最小 sum possible 可能的最大總和 |
|
3 和更高 |
12 |
|
4 和 higher |
15 |
|
5 和 higher |
18 |
|
6 和 higher |
21 |
|
7 和 higher |
24 |
10) 使用三個不同的數字,這些數字都大於或等於 11,最小的可能總和是多少?
11) 使用三個不同的數字,這些數字都大於或等於 20,最小的可能總和是多少?
12) 使用三個不同的數字,這些數字都大於或等於 100,最小的可能總和是多少?
13) 你能確定 10x10 數獨中一個三格的橫排籠子,目標為 8 的最大可能數字嗎?
14) 你能確定 10x10 數獨中一個三格的橫排籠子,目標為 9 的最大可能數字嗎?
15) 在以下表格中找到模式。
|
目標 sum of a 3 square row cage
|
10 |
11 |
12 |
13 |
|
可能的最大數字 |
7 |
8 |
9 |
10 |
16) 如果目標總和為 22,10x10 數獨中一個三格籠子的最小可能數字是多少?
17) 如果目標總和為 23,10x10 數獨中一個三格籠子的最小可能數字是多少?
18) 如果目標總和為 24,10x10 數獨中一個三格籠子的最小可能數字是多少?
19) 如果目標總和為 25,10x10 數獨中一個三格籠子的最小可能數字是多少?
20) 你能識別下表中的模式嗎?
三個格線性籠子的目標總和 格線性籠子 |
26 |
27 |
28 |
29 |
10x10 數獨的最小可能數字 |
7 |
8 |
9 |
10 |
21) 對於 10x10 數獨中一個三格線性籠子的目標總和為 29,識別下表中的模式。
|
大小 of puzzle |
13x13 |
12x12 |
11x11 |
|
最小可能數字 |
4 |
6 |
8 |
22) 在 14x14 數獨中,目標總和為 29 的最小可能數字是多少?
23) 對於一個目標總和為 11 的四格線性籠子,最大的可能數字是多少?給出你的理由。
24) 對於一個目標總和為 12 的四格線性籠子,最大的可能數字是多少?給出你的理由。
25) 對於一個目標總和為 13 的四格線性籠子,最大的可能數字是多少?給出你的理由。
26) 識別下表中的模式
|
目標 sum in linear four-square cage
|
14 |
15 |
16 |
17 |
18 |
|
可能的最大數字 |
8 |
9 |
10 |
11 |
12 |
27) 對於 11x11 中一個目標總和為 34 的四格橫排籠子,最小的可能數字是多少?
28) 對於 11x11 中一個目標總和為 35 的四格橫排籠子,最小的可能數字是多少?
29) 對於 11x11 中一個目標總和為 36 的四格橫排籠子,最小的可能數字是多少?
30) 對於 11x11 中一個目標總和為 37 的四格橫排籠子,最小的可能數字是多少?
31) 對於 12x12 中一個目標總和為 34 的四格橫排籠子,最小的可能數字是多少?
32) 對於 12x12 中一個目標總和為 35 的四格橫排籠子,最小的可能數字是多少?
33) 對於 12x12 中一個目標總和為 36 的四格橫排籠子,最小的可能數字是多少?
34) 對於 12x12 中一個目標總和為 37 的四格橫排籠子,最小的可能數字是多少?
35) 識別以下表格中的模式。
|
大小 |
12 |
12 |
12 |
13 |
13 |
13 |
13 |
13 |
14 |
14 |
14 |
|
目標 |
38 |
39 |
40 |
38 |
39 |
40 |
41 |
42 |
40 |
41 |
42 |
最小 的可能數字 |
5 |
6 |
7 |
2 |
3 |
4 |
5 |
6 |
1 |
2 |
3 |
36) 反思你在這次探索中學到的東西。寫下你學到的一些東西。
答案
(1)
6x6 數獨中三格線性籠子的目標總和 |
必須存在 |
必須不存在 |
可能存在 |
6 |
1, 2, 3 |
4, 5, 6 |
|
7 |
1, 2, 4 |
3, 5, 6 |
|
8 |
1 |
6 |
2, 3, 4, 5 |
9 |
1, 2, 3, 4, 5, 6 | ||
10 |
1, 2, 3, 4, 5, 6 | ||
11 |
1, 2, 3, 4, 5, 6 | ||
12 |
1, 2, 3 ,4, 5, 6 | ||
13 |
6 |
1 |
2, 3, 4, 5 |
14 |
3, 5, 6 |
1, 2, 4 |
|
15 |
4, 5, 6 |
1, 2, 3 |
2) 對於 20x20 數獨中一個三格籠子的目標總和為 8,5 是最大的可能數字。
3) 對於 20x20 數獨中一個三格籠子的目標總和為 49,10 是最小的可能數字。
4) 對於 11x11 數獨中一個四格橫排籠子的目標總和為 35,5 是最小的可能數字。
5) 對於 20x20 數獨中一個四格橫排籠子的目標總和為 11,5 是最大的可能數字。
6)
12x12 數獨中三格線性籠子的目標總和 |
必須存在 |
必須不存在 |
可能存在 |
6 |
1, 2, 3 |
4 和更高 |
|
7 |
1, 2, 4 |
3、5 和更高 |
|
8 |
1 |
6 和更高 |
2, 3, 4, 5 |
9 |
7 和更高 |
1, 2, 3, 4, 5, 6 | |
10 |
8 和更高 |
1, 2, 3, 4, 5, 6, 7 | |
29 |
5 或更小 |
6 或更高 | |
30 |
6 或更小 |
7 或更高 | |
31 |
12 |
7 或更小 |
8, 9, 10, 11 |
32 |
9, 11, 12 |
10、8 或更小 |
|
33 |
10,11,12 |
9 或更小 |
7) 以下是一些尋找差異的策略
比較連續的行,尋找相似之處。
比較連續的行,尋找差異。
檢視連續數字之間的差異,並在差異中尋找模式。
表格中的模式包括以下內容
- 總和都是 3 的倍數。
- 允許的數字從一行到下一行增加一個數字。
- 總和在每行連續增加 3。
- 最大總和是三個最大數字的總和。
- 最大總和是 3 x(最大數字 - 3)。
- 最大總和是第二大數字的 3 倍。
8) 根據我們在上一個問題的分析中觀察到的模式,我們預計使用 1 到 100 的數字,可能的最大總和將是 297。原因是可能的最大總和將是最大的三個數字,即 98、99 和 100。因此,這個總和將是 98 + 99 + 100 = 297。
9) 以下是一些尋找差異的策略
比較連續的行,尋找相似之處。
比較連續的行,尋找差異。
檢視連續數字之間的差異,並在差異中尋找模式。
表格中的模式包括以下內容
總和都是 3 的倍數。
允許的數字從一行到下一行增加一個數字。
總和在每行連續增加 3。
最小總和是三個最小數字的總和。
最小總和是三個最小數字的總和 + 3。
最小總和是第二小數字的 3 倍。
10) 使用三個不同的數字,這些數字都大於或等於 11,最小的可能總和是 36。
11) 使用三個不同的數字,這些數字都大於或等於 20,最小的可能總和是 63。
12) 使用三個不同的數字,這些數字都大於或等於 100,最小的可能總和是 303。
13) 10x10 數獨中一個三格橫排籠子,目標為 8 的最大可能數字是 5。
14) 10x10 數獨中一個三格橫排籠子,目標為 9 的最大可能數字是 6。
15) 模式包括以下內容
連續列中的數字增加 1。
一種策略是檢視兩列值的差異。在這裡,我們發現差異始終是 3。因此,另一個相關的模式是:
可能的最大數字是目標總和減 3。
解釋這種模式的一種方法如下。當我們使用可能的最大數字時,其餘兩個數字的總和將是最小的可能總和。我們用兩個不同的數字可以建立的最小總和將是 1 和 2 的總和,即 3。因此,籠子中可以使用 的最大可能數字是目標總和減 3。
16) 如果目標總和為 22,10x10 數獨中一個三格籠子的最小可能數字是 3。
17) 如果目標總和為 23,10x10 數獨中一個三格籠子的最小可能數字是 4。
18) 如果目標總和為 24,10x10 數獨中一個三格籠子的最小可能數字是 5。
19) 如果目標總和為 25,10x10 數獨中一個三格籠子的最小可能數字是 6。
20) 模式:最小可能數字 = 目標總和 - 19
21) 模式
謎題的大小在連續列中減小 1。
最小數字在連續列中增加 1。
對於 m * m 數獨中目標總和為 x 的三格籠子,如果這個數字為正,則最小可能數字是 x - m - (m - 1)。
22) 使用上面的模式,我們得出結論是 2。
23) 對於一個目標總和為 11 的四格線性籠子,5 是最大的可能數字。最大的可能數字將對應於剩餘三個數字建立的最小總和。三個數字可以建立的最小總和將是 1 + 2 + 3 = 6。因此,最大的可能數字將是 11 - 6 = 5。
24) 對於一個目標總和為 12 的四格線性籠子,6 是最大的可能數字。給出你的理由。最大的可能數字將對應於剩餘三個數字建立的最小總和。三個數字可以建立的最小總和將是 1 + 2 + 3 = 6。因此,最大的可能數字將是 12 - 6 = 6。
25) 對於一個目標總和為 13 的四格線性籠子,7 是最大的可能數字。給出你的理由。最大的可能數字將對應於剩餘三個數字建立的最小總和。三個數字可以建立的最小總和將是 1 + 2 + 3 = 6。因此,最大的可能數字將是 13 - 6 = 7。
26) 識別下表中的模式
四格線性籠子的目標總和 |
14 |
15 |
16 |
17 |
18 |
可能的最大數字 |
8 |
9 |
10 |
11 |
12 |
在一個線性四格籠中,最大的可能數字是 T - 6,其中 T 是目標總和。這種模式可以解釋如下。最大的可能數字對應於其餘三個數字產生的最小總和。三個數字可以產生的最小總和是 1 + 2 + 3 = 6。因此,最大的可能數字是 T - 6。
27) 對於一個目標總和為 34 的 11x11 四格行籠,最小的可能數字是 4。
28) 對於一個目標總和為 35 的 11x11 四格行籠,最小的可能數字是 5。
29) 對於一個目標總和為 36 的 11x11 四格行籠,最小的可能數字是 6。
30) 對於一個目標總和為 37 的 11x11 四格行籠,最小的可能數字是 7。
31) 對於一個目標總和為 34 的 12x12 四格行籠,最小的可能數字是 1。
32) 對於一個目標總和為 35 的 12x12 四格行籠,最小的可能數字是 2。
33) 對於一個目標總和為 36 的 12x12 四格行籠,最小的可能數字是 3。
34) 對於一個目標總和為 37 的 12x12 四格行籠,最小的可能數字是 4。
35) 表格中存在多種模式。
最小的可能數字 = 目標 - 3 * (尺寸 -1)
|
大小 |
12 |
12 |
12 |
13 |
13 |
13 |
13 |
13 |
14 |
14 |
14 |
|
目標 |
38 |
39 |
40 |
38 |
39 |
40 |
41 |
42 |
40 |
41 |
42 |
|
最小 的可能數字 |
5 |
6 |
7 |
2 |
3 |
4 |
5 |
6 |
1 |
2 |
3 |
這也可以寫成以下形式
最小的可能數字是 T - L,如果 L 是用三個數字可以組成的最大總和。
邏輯圖表探索
[edit | edit source]練習
- Max,Yao 和 Naz 分別坐在 A,B 和 C 座位上。Max 不坐在 B 座位上。Yao 坐在 A 座位上。每個人坐在哪裡?
- 考慮下面列出的 6x6 KenKen 謎題中的兩行。你能確定哪個數字會進入目標為 2/ 的籠子嗎?
1 |
2 |
3 |
4 |
5 |
6 | |
A |
18x |
??? |
??? |
??? |
??? |
15x |
|
B |
2/ |
|||||
解答
1) 對於某些型別的謎題,圖形化表示有助於理解線索的描述。在問題 1 中描述的謎題中,一個捕獲人與座位之間所有關聯的表示形式很有用。這種型別的表示形式如下所示。這被稱為邏輯網格。
|
座位 A |
座位 B |
座位 C | |
|
Max |
|||
|
Yao |
|||
|
Naz |
現在讓我們檢查一下如何使用這種邏輯圖表來解釋每條線索。我們被告知 Yao 先生坐在 A 座位上。當你閱讀每條線索時,劃掉與線索不一致的方格。例如,一句話告訴你 Yao 先生坐在 A 座位上,你就可以確定他沒有坐在 B 或 C 座位上。
|
座位 A |
座位 B |
座位 C | |
|
Max |
|||
|
Yao |
Yes |
X |
X |
|
Naz |
一旦你確定 Yao 先生坐在 A 座位上;那麼你就可以排除任何其他人坐在 A 座位上的可能性。正如你所看到的,這確實縮小了選擇範圍,並幫助你朝著解決方案努力。
因此,圖表如下所示。
|
座位 A |
座位 B |
座位 C | |
|
Max |
X |
||
|
Yao |
Yes |
X |
X |
|
Naz |
X |
現在,讓我們在這個表中表示第二條線索。Max 不坐在 B 座位上。
|
座位 A |
座位 B |
座位 C | |
|
Max |
X |
X |
|
|
Yao |
Yes |
X |
X |
|
Naz |
X |
如果我們知道 Max 坐在三個座位中的一個,並且我們已經推斷出他不能坐在三個座位中的兩個,那麼 Max 必須坐在剩下的座位上。因此,在這種情況下,我們可以推斷出 Max 坐在 C 座位上。
|
座位 A |
座位 B |
座位 C | |
|
Max |
X |
X |
Yes |
|
Yao |
Yes |
X |
X |
|
Naz |
X |
如果我們知道 Max 坐在 C 座位上,那麼 Yao 或 Naz 就不能坐在 C 座位上。讓我們將此資訊新增到我們的邏輯圖表中。
|
座位 A |
座位 B |
座位 C | |
|
Max |
X |
X |
Yes |
|
Yao |
Yes |
X |
X |
|
Naz |
X |
X |
如果我們知道 Yao 坐在三個座位中的一個,並且我們已經推斷出他不能坐在三個座位中的兩個,那麼 Naz 必須坐在剩下的座位上。因此,在這種情況下,我們可以推斷出 Naz 坐在 B 座位上。現在,讓我們將此資訊新增到我們的邏輯圖表中。
|
座位 A |
座位 B |
座位 C | |
|
Max |
X |
X |
Yes |
|
Yao |
Yes |
X |
X |
|
Naz |
X |
Yes |
X |
現在,我們已經用“Yes”或“X”填充了邏輯圖表中的所有條目。因此,我們已經解決了謎題。我們知道 Max 坐在 C 座位上。Yao 坐在 A 座位上,Naz 坐在 B 座位上。
2) 讓我們檢查一下 1 到 6 之間滿足 2/ 約束的數字對。
1 |
2 |
3 |
4 |
5 |
6 | |
A |
18x |
??? |
??? |
??? |
??? |
15x |
|
B |
2/ |
|||||
我們發現 (6, 3), (4, 2) 和 (2, 1) 這對數字都可以滿足 2/ 約束。因此,1、2、3、4 或 6 中的任何數字都可以作為底行中的第三或第四個方格。現在,讓我們檢查一下哪些三元組可以滿足 18x 約束。我們發現 <3, 2, 3> 和 <6, 3, 1> 可以滿足 18x 約束。因此,1、2、3 或 6 中的任何數字都可以作為底行的第一個或第二個方格。類似地,<5, 3, 1> 可以滿足 15x 約束。因此,數字 1、3、5 可能出現在底行的第五或第六個方格中。
以下是我們的邏輯謎題線索
|
籠子 |
1 |
2 |
3 |
4 |
5 |
6 |
|
18x |
可能 |
可能 |
可能 |
可能 | ||
|
2/ |
可能 |
可能 |
可能 |
可能 |
可能 | |
|
15x |
可能 |
可能 |
可能 |
由於 4 必須出現在一個方格中,而只有 2/ 籠子將其列為可能性,因此我們可以得出結論,4 必須在 2/ 籠子中。因此,2/ 籠子中必須有 2 和 4 作為數字。現在我們可以修改邏輯圖表如下所示。
|
籠子 |
1 |
2 |
3 |
4 |
5 |
6 |
|
18x |
可能 |
可能 |
可能 |
可能 | ||
|
2/ |
可能 |
可能 |
||||
|
15x |
可能 |
可能 |
可能 |
由於 6 必須出現在一個方格中,而只有 18x 籠子將其列為可能性,因此我們可以得出結論,6 必須在 18x 籠子中。因此,18x 中的其他數字必須是 6、3 和 1。現在我們可以修改邏輯圖表如下所示。
|
籠子 |
1 |
2 |
3 |
4 |
5 |
6 |
|
18x |
可能 |
可能 |
可能 | |||
|
2/ |
可能 |
可能 |
||||
|
15x |
可能 |
可能 |
可能 |
由此,我們可以得出以下結論
2/ 籠子中包含 2 和 4。18x 籠子中包含 1、3 和 6。15x 籠子中包含 1、3 和 5。
和與差的探索
[edit | edit source]考慮以下問題
我們有一組十個數字。在這組數字中,數字 1 到 10 每個數字都只出現一次,但並不一定按升序排列。前八個數字加起來是 45。最後兩個數字的差是 2。最後兩個數字是什麼?
大多數學生試圖解決這個問題的策略是“猜測和檢查”。例如,他們可能會提出 (2, 3, 4, 5, 6, 7, 8) 這樣的組合,並發現剩餘兩個數字的差值不是 2。使用猜測和檢查策略可能需要很長時間才能找到這個問題的解決方案。
我們可能認為我們陷入了困境。我們需要一些見解才能在問題上取得進展。在這種情況下,一種策略是簡化問題或考慮一個類似的問題。
我們可以考慮在 6x6 謎題中瞭解類似的情況。考慮以下練習。
練習 1:檢視圖 1 中的具體示例,並確定其中的任何模式。
練習 1 的解決方案:人們可能會觀察到各種模式。這些示例包括以下內容
- 當第五個數字增加 1 時,第一個籠子的目標總和也減少 1。
- 當第六個數字增加 1 時,第一個籠子的目標總和也減少 1。
- 第一個籠子的目標總和 = 21 - a - b,如果 a 和 b 是第五和第六個數字。
- 第五和第六個數字的總和 = 21 - 第一個籠子的目標總和。
- 當第一個籠子中的一個數字增加 1 且該籠子中的其他數字保持不變時,第二個籠子中的一個數字減少 1。
- 當第一個籠子中的一個數字增加 1 且該籠子中的其他數字保持不變時,該籠子的目標總和增加 1。
- 如果我們將第一個籠子中的一個數字增加 1,那麼該籠子的目標總和就會增加 1。
練習 2:我們能否解釋為什麼第五和第六個數字的總和等於 21 與第一個籠子的目標總和之差?
練習 2 的解決方案:關於最後兩個數字總和的模式允許推斷出最後兩個數字的總和。有時,當我們建立數學模型時,數字關係會變得更加清晰。假設一個總和籠子的目標是 a,籠子外剩餘數字的總和是 b。我們還知道該行中的所有數字都是 1 到 6。因此,所有數字加起來將是 1 + 2 + 3 + 4 + 5 + 6 = 21。
因此,我們可以說
a + b = 1 + 2 + 3 + 4 + 5 + 6
這是關於該行數字推理的數學模型。
它可以在數學上進行操作。
例如,我們可以寫
b = 21 - a。
因為我們知道 a 的值,所以我們也可以透過求解這個方程來確定 b 的值。如果我們知道 b,那麼我們就知道一個額外的約束條件,即最後兩個數字加起來會是 b。在某些問題中,這將允許我們做出進一步的推斷。現在考慮以下問題
假設最後兩個數字是 x 和 y。然後,-2 目標告訴我們 x - y = 2。此外,根據我們之前討論的內容,最後兩個數字將加起來是 4。此外,我們被告知它們之間的差值是 2。
這可以寫成
x - y = 2
x + y = 4。
同樣,我們在這裡建立了一個數學模型。建立這樣的模型將允許我們理解解決這類問題的策略,這些策略將在 KenKen 謎題中以不同的形式反覆出現。
現在,我們需要一個過程來確定這兩個數字。
由於問題涉及兩個未知變數,因此一種策略是猜測和檢查。在這種情況下,你可能在進行幾次猜測後就能得到答案。由於 x 和 y 的總和是 4,因此它們中的每一個最多可以是 4。可以建立一個表,列出 x 和 y 的可能值以及它們的對應總和。如下表所示。
|
x |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
|
y |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
x + y |
2 |
3 |
4 |
5 |
1 |
3 |
4 |
|
x- y |
0 |
1 |
2 |
3 |
0 |
1 |
2 |
然後,人們可以在表中確定兩個數字的總和為 4 且兩個數字之差為 2 的值。匹配的數字是 x = 3 且 y = 1。
現在,讓我們檢查一下解決這個問題的其他方法。有時,當問題的解決方案不明顯時,我們可以將問題資訊用圖表表示,然後解決方案就變得很明顯了。下面是一個這樣的表示。
從視覺上,我們可以看到 x + y 與 x - y 之間的差值是 2y。
因此,2y = 4 - 2。
因此,2y = 2。
將兩邊都除以 2,我們得到
y = 1。
一旦我們得到 y 的值,我們就可以將其代入方程 x + y = 4 中
這將給我們 x + 1 = 4。
現在,從方程兩邊減去 1,我們將得到
x + 1 - 1 = 4 - 1。
因此,x = 3。
下面,我們提供了一個簡單的三步程式來確定和為 a、差為 b 的數字。
- 設 x 和 y 是這兩個數字。計算 y 為 (a - b) / 2。
- 將 y 的值代入方程 x + y = a。
- 簡化此方程以計算 x 的值。
這是因為 (x + y) + (x - y) = 2x = a + b。
類似地,(x + y) - (x - y) = 2y = a – b。
練習
對於下表中的每個問題,找到 x 和 y。使用兩種方法解決此問題:繪製圖表和使用本章中描述的三步程式。
|
問題 Number |
x + y |
x -y |
x 是多少? |
y 是多少? |
1 |
4 |
12 |
||
2 |
6 |
20 |
||
3 |
12 |
32 |
||
4 |
100 |
140 |
||
5 |
3 |
9 |
||
6 |
17 |
19 |
||
7 |
25 |
27 |
||
8 |
25 |
77 |
||
9 |
50 |
90 |
||
10 |
220 |
300 |
答案
|
問題 Number |
x + y |
x -y |
x 是多少? |
y 是多少? |
|
1 |
4 |
12 |
8 |
4 |
|
2 |
6 |
20 |
13 |
7 |
|
3 |
12 |
32 |
22 |
10 |
|
4 |
100 |
140 |
120 |
20 |
|
5 |
3 |
9 |
6 |
3 |
|
6 |
17 |
19 |
18 |
1 |
|
7 |
25 |
27 |
26 |
1 |
|
8 |
25 |
77 |
51 |
26 |
|
9 |
50 |
90 |
70 |
20 |
|
10 |
220 |
300 |
260 |
40 |
在 KenKen 謎題中確定一行中最右邊兩個數字的步驟,其中最右邊的籠子有減法目標 n,包含兩個方格,其餘方格在一個目標總和為 m 的籠子裡。
- 將 KenKen 謎題中允許的所有數字加起來。
- 計算最右邊兩個數字的總和,使其等於步驟 (1) 中的結果減去 m。
- 最右邊兩個數字之間的差值為 n。
- 現在,使用上面描述的程式確定數字,該程式確定和與差已知的數字。
現在考慮我們之前討論的問題
我有一個包含十個數字的列表。在這個列表中,數字 1 到 10 每個都只出現一次,但不一定按升序排列。前八個數字加起來是 45。最後兩個數字之間的差值為 2。最後兩個數字是什麼?
將 1 到 10 之間的數字全部加起來,得到 55。
因為前八個數字加起來是 45,所以最右邊數字的總和將是 55 - 45 = 10。
最右邊兩個數字之間的差值為 2。
因此,使用從和與差中查詢數字的步驟,我們可以確定這些數字為 6 和 4。
答案:6 和 4
練習
我有一個包含六個數字的列表。這些數字是 1 到 6,但不一定按相同的順序排列。
下表中的每一行都指定了前四個數字的總和以及最後兩個數字之間的差值,嘗試確定最後兩個數字。每一行都有不同的答案。
前 四個數字 的總和 |
最後 兩個數字 之間的差值 |
14 |
5 |
13 |
2 |
14 |
1 |
17 |
2 |
14 |
3 |
13 |
4 |
15 |
2 |
12 |
1 |
16 |
3 |
15 |
4 |
12 |
3 |
解答
各位數字之和 |
差值 |
較大的數字 |
較小數字 |
14 |
5 |
6 |
1 |
13 |
2 |
5 |
3 |
14 |
1 |
4 |
3 |
17 |
2 |
3 |
1 |
14 |
3 |
5 |
2 |
13 |
4 |
6 |
2 |
15 |
2 |
4 |
2 |
12 |
1 |
5 |
4 |
16 |
3 |
4 |
1 |
15 |
4 |
5 |
1 |
12 |
3 |
6 |
3 |
乘積和差值的探索
[edit | edit source]練習
1) 考慮以下問題
我有一個包含八個數字的列表。在這個列表中,數字 1 到 8 每個都只出現一次,但不一定按升序排列。前六個數字的乘積是 720。最後兩個數字之間的差值為 1。最後兩個數字是什麼?
嘗試使用猜想和檢查策略來解決問題,你猜測數字。如果你得到答案,記下來。嘗試確定在這個問題上使用猜想和檢查策略的困難之處。
2) 下表中的每一行都列出了一個包含 6 個數字的不同列表的屬性,這些數字來自 1 到 6,但順序不同。你在這張表中觀察到什麼模式?
前 四個數字 |
最後 兩個數字 |
前 四個 數字的乘積 |
最後 兩個 數字的乘積 |
最後 兩個 數字之間的差值 |
|
1, 2, 3, 4 |
5, 6 |
24 |
30 |
1 |
|
1, 2, 3, 5 |
4, 6 |
30 |
24 |
2 |
|
1, 2, 4, 5 |
3, 6 |
40 |
18 |
3 |
|
1, 3, 4, 5 |
2, 6 |
60 |
12 |
4 |
|
2, 3, 4, 5 |
1, 6 |
120 |
6 |
5 |
3) 下表中的每一行都列出了一個包含六個數字的不同列表的屬性,這些數字來自 1 到 6,但順序不同。你在這張表中觀察到什麼模式?
前 四個數字 |
最後 兩個數字 |
前 四個 數字的乘積 |
最後 兩個 數字之間的差值 |
|
1,2 , 3, 4 |
5, 6 |
24 |
1 |
|
2, 3, 4, 5 |
1, 6 |
120 |
5 |
|
1, 3, 4, 5 |
2, 6 |
60 |
4 |
|
2, 3, 4, 5 |
1, 6 |
120 |
5 |
|
1, 2, 4, 5 |
3, 6 |
40 |
3 |
|
2, 3, 4, 5 |
1, 6 |
120 |
5 |
4) 我們有一個包含 1 到 6 的六個數字的列表,但順序不一定相同。前四個數字的乘積是 24。我們正在嘗試確定最後兩個數字的乘積。我們知道所有六個數字的乘積 = 1 x 2 x 3 x 4 x 5 x 6 = 720。假設最後兩個數字的乘積是 p。
720 = 所有六個數字的乘積
因此,720 = 前四個數字的乘積乘以最後兩個數字的乘積。
因此,我們確定 720 = 24 x p。從此確定 p 的值。
5) 我們得到了兩個神秘數字 x 和 y,它們可以是 1、2、3、4、5 或 6。我們被告知
x - y = 1。
x * y = 30。
你能從這些資訊中確定 x 和 y 嗎?一種可能的方法是建立一個包含 x 和 y 的可能值的表格,並檢查給定的約束條件是否為真。
6) 我們被告知兩個數字之間的差值為 4,這兩個數字的乘積為 32。我們想要確定這兩個數字的總和。
- 這兩個數字之間的差值是多少?
- 這兩個數字之間的差值的平方是多少?
- 4 乘以這兩個數字的乘積是多少?
- (B) 和 (C) 的結果之和是多少?
- (D) 的平方根是多少?
- 這兩個數字的總和是多少?
7) 我們被告知兩個數字之間的差值為 2,這兩個數字的乘積為 8。我們想要確定這兩個數字的總和。
- 這兩個數字之間的差值是多少?
- 這兩個數字之間的差值的平方是多少?
- 4 乘以這兩個數字的乘積是多少?
- (B) 和 (C) 的結果之和是多少?
- (D) 的平方根是多少?
- 這兩個數字的總和是多少?
8) 我們被告知兩個數字之間的差值為 1,這兩個數字的乘積為 30。我們想要確定這兩個數字的總和。
- 這兩個數字之間的差值是多少?
- 這兩個數字之間的差值的平方是多少?
- 4 乘以這兩個數字的乘積是多少?
- (B) 和 (C) 的結果之和是多少?
- (D) 的平方根是多少?
- 這兩個數字的總和是多少?
9) 我們被告知兩個數字之間的差值為 3,這兩個數字的乘積為 18。我們想要確定這兩個數字的總和。
- 這兩個數字之間的差值是多少?
- 這兩個數字之間的差值的平方是多少?
- 4 乘以這兩個數字的乘積是多少?
- (B) 和 (C) 的結果之和是多少?
- (D) 的平方根是多少?
- 這兩個數字的總和是多少?
10) 我們被告知兩個數字之間的差值為 1,這兩個數字的乘積為 42。我們想要確定這兩個數字的總和。
- 這兩個數字之間的差值是多少?
- 這兩個數字之間的差值的平方是多少?
- 4 乘以這兩個數字的乘積是多少?
- (B) 和 (C) 的結果之和是多少?
- (D) 的平方根是多少?
- 這兩個數字的總和是多少?
11) 我們被告知兩個數字之間的差值為 3,這兩個數字的乘積為 4。我們想要確定這兩個數字的總和。
- 這兩個數字之間的差值是多少?
- 兩個數字之間的差值的平方是多少?
- 4 乘以這兩個數字的乘積是多少?
- (B) 和 (C) 的結果之和是多少?
- (D) 的平方根是多少?
- 這兩個數字的總和是多少?
12) 我們被告知兩個數字之間的差值為 4,這兩個數字的乘積為 12。我們想要確定這兩個數字的總和。
- 這兩個數字之間的差值是多少?
- 這兩個數字之間的差值的平方是多少?
- 4 乘以這兩個數字的乘積是多少?
- (B) 和 (C) 的結果之和是多少?
- (D) 的平方根是多少?
- 這兩個數字的總和是多少?
13) 如果給你兩個正數之間的和與差值,那麼你可以使用下面的公式找到這兩個數
較大數字 = (和 + 差)/2
較小數字 = (和 - 差)/2
(a) 兩個數字的總和是 12。它們的差值為 4。較大的數字是多少?較小的數字是多少?
(b) 兩個數字的總和是 6。它們的差值為 2。較大的數字是多少?較小的數字是多少?
(c) 兩個數字的總和是 11。兩個數字之間的差值為 1。較大的數字是多少?較小的數字是多少?
(d) 兩個數字的總和是 9。兩個數字之間的差值為 3。較大的數字是多少?較小的數字是多少?
(e) 兩個數字的總和是 13。兩個數字之間的差值為 1。較大的數字是多少?較小的數字是多少?
(f) 兩個數字的總和是 5。兩個數字之間的差值為 3。較大的數字是多少?較小的數字是多少?
(g) 兩個數字的總和是 8。兩個數字之間的差值為 4。較大的數字是多少?較小的數字是多少?
14) 對於下表中的每個問題,找到 x 和 y。
|
問題 Number |
x * y |
x -y |
是什麼 x? |
是什麼 y? |
|
1 |
32 |
12 |
||
|
2 |
8 |
2 |
||
|
3 |
30 |
1 |
||
|
4 |
18 |
3 |
||
|
5 |
42 |
1 |
||
|
6 |
4 |
3 |
||
|
7 |
12 |
4 |
15) 現在,讓我們考慮第一個問題。
我有一個包含 8 個數字的列表。在這個列表中,數字 1 到 8 每個都只出現一次,但不一定按升序排列。前六個數字的乘積是 720。最後兩個數字之間的差值為 1。最後兩個數字是什麼?
(a) 從 1 到 8 的所有數字的乘積是多少?
(b) 如果 720 * a = 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8,那麼 a 是多少?
(c) 如果兩個數字之間的差值為 1,並且它們的乘積由上一個問題的答案給出,那麼這兩個數字的總和是多少?
(d) 如果數字的總和由上一個問題的答案給出,並且兩個數字之間的差值為 1,那麼這兩個數字是什麼?
16) 你能確定下表中給出前兩個數字之間的差值和最後四個數字的乘積的情況下,第一個籠子中的兩個數字是什麼?每一行對應於一個不同的問題,並且具有不同的解決方案。
|
差值 between first two
|
的乘積 last four
|
較大的數字 |
較小 number |
|
4 |
144 |
||
|
2 |
30 |
||
|
1 |
360 |
||
|
1 |
120 |
||
|
3 |
72 |
||
|
3 |
40 |
||
|
3 |
180 |
||
|
1 |
60 |
||
|
2 |
48 |
||
|
5 |
120 |
||
|
2 |
90 |
||
|
1 |
36 |
||
|
1 |
24 |
17) 回顧並確定你在這次探索中學習到的某些東西。
解答
1. 學生在解決這個問題時最常使用的一種策略是猜想和檢查。雖然這種策略可以找到解決方案,但它是一個耗時的策略,需要大量的計算。
2. 在這些例子中,人們可以觀察到各種模式,包括以下模式
隨著最後兩個數字變小,前四個數字的乘積會增加。最後兩個數字的乘積和前四個數字的乘積始終為 720。
3. 在這些例子中,人們可以觀察到各種模式,包括以下模式
如果第五個數字是 a 並且它被 1 替換,則前四個數字的乘積將乘以 a。最後兩個數字的乘積和前四個數字的乘積始終為 720。
4. p 是 30。
5. x 是 6,y 是 5。
6. (a) 12 (b) 16 (c) 128 (d) 144 (e) 12 (f) 12。
7. (a) 2 (b) 4 (c) 32 (d) 36 (e) 6 (f) 6。
8. (a) 1 (b) 1 (c) 120 (d) 121 (e) 11 (f) 11。
9. (a) 3 (b) 9 (c) 72 (d) 81 (e) 9 (f) 9。
10. (a) 1 (b) 1 (c) 168 (d) 169 (e) 13 (f) 13。
11. (a) 3 (b) 9 (c) 16 (d) 25 (e) 5 (f) 5。
12. (a) 4 (b) 16 (c) 48 (d) 64 (e) 8 (f) 8。
13. (a) 8 和 4 (b) 4 和 2 (c) 10 和 9 (d) 6 和 3 (e) 7 和 6 (f) 4 和 1 (g) 6 和 2。
14.
問題編號 |
x * y |
x - y |
x 是多少? |
y 是多少? |
1 |
32 |
12 |
8 |
4 |
2 |
8 |
2 |
4 |
2 |
3 |
30 |
1 |
6 |
5 |
4 |
18 |
3 |
6 |
3 |
5 |
42 |
1 |
7 |
6 |
6 |
4 |
3 |
4 |
1 |
7 |
12 |
4 |
6 |
2 |
15. (a) 40320 (b) 56 (c) 15 (d) 7 and 8.
16.
前兩個數的差 |
最後四個數的乘積 |
較大的數字 |
較小的數 |
|
4 |
144 |
5 |
1 |
|
2 |
30 |
6 |
4 |
|
1 |
360 |
2 |
1 |
|
1 |
120 |
3 |
2 |
|
3 |
72 |
5 |
2 |
|
3 |
40 |
6 |
3 |
|
3 |
180 |
4 |
1 |
|
1 |
60 |
4 |
3 |
|
2 |
48 |
5 |
3 |
|
5 |
120 |
6 |
1 |
|
2 |
90 |
4 |
2 |
|
1 |
36 |
5 |
4 |
|
1 |
24 |
6 |
5 |
17. 剛開始,你可能會卡住。但是,探索類似但更簡單的問題情況可以為我們提供解決問題的見解。雖然猜想和檢查是一種可以用於解決此問題的策略,但我們學習了另一種涉及數字和差的解決問題的方法。
練習
1) 考慮以下問題
我有一組十個數。在這組數中,數字 1 到 10 每個都出現一次,但不一定按升序排列。前八個數的和為 46。最後兩個數的比率為 2。最後兩個數是什麼?
嘗試使用猜想和檢查策略來解決問題,你猜測數字。如果你得到答案,記下來。嘗試確定在這個問題上使用猜想和檢查策略的困難之處。
2) 解決以下問題
a. 數字 1 到 10 的總和是多少?
b. 如果前八個數加起來是 46,最後兩個數的和是多少?
3) 建立一個表格,第一列的值從 1 到 4 變化,第二列的值是第一列值的兩倍,第三列的值是前兩列的值之和,第四列的值是第二列的值除以第一列的值。
4) 如果兩個數的和是 9 且其比率是 2,這兩個數是什麼?
5) 現在,讓我們練習一下關於根據數字的和與積來確定未知數字的技能。
下表中的每一行都是一個不同的問題。在每種情況下確定兩個未知數。
|
問題 Number |
數字的和 |
數字的比率 numbers |
數字 |
1 |
27 |
2 |
|
2 |
54 |
2 |
|
3 |
81 |
2 |
|
4 |
60 |
2 |
|
5 |
44 |
3 |
|
6 |
60 |
3 |
|
7 |
400 |
3 |
|
8 |
60 |
4 |
觀察完表中問題的解題方法後,你能發現任何與數字及其和與比率相關的模式嗎?
6) 一個 10x10 的數獨謎題的第一行有兩個水平籠子。第一個是一個八個方格的籠子,目標和為 S。第二個是一個兩個方格的籠子,除法目標為 R。嘗試確定這些數字。
問題編號 |
S |
R |
找出這些數字 |
1 |
45 |
4 |
|
2 |
52 |
2 |
|
3 |
43 |
2 |
|
4 |
40 |
2 |
7) 你能發現先前問題解題方法中的模式嗎?
8) 一個 9x9 的數獨謎題的第一行有兩個水平籠子。第一個是一個七個方格的籠子,目標和為 S。第二個是一個兩個方格的籠子,除法目標為 R。嘗試確定這些數字。
問題編號 |
各位數字之和 |
比率 |
找出這些數字 |
1 |
41 |
3 |
|
2 |
33 |
2 |
|
3 |
43 |
3 |
|
4 |
30 |
2 |
9) 你能發現先前問題解題方法中的模式嗎?
解答
1) 學生們在這道題上使用最多的策略是猜想和檢查。雖然這種策略可以找到解,但它是一種費時且涉及大量計算的策略。因為它涉及大量計算,所以這種策略也容易出錯。
2) 數字 1 到 10 的總和是 55。如果最後兩個數字加起來為 a,那麼我們可以寫成如下形式
前八個數的和 + 所有數字對的和 = 所有等於 55 的數字的和。
我們知道前八個數的和是 46。
所以,46 + a = 55。
我們可以透過從兩邊減去 46 來簡化它。
46 + a - 46 = 55 – 46.
a + 0 = 9.
因此,a 必須是 9。
3)
|
第一個 Number |
第二個數字 |
各位數字之和 |
比率 |
|
1 |
2 |
3 |
2 |
|
2 |
4 |
6 |
2 |
|
3 |
6 |
9 |
2 |
|
4 |
8 |
12 |
2 |
4) 假設,最後兩個數字中較小的那個是 a。由於兩個數字的比率是 2,那麼這兩個數字是 a 和 2a。由於我們知道這兩個數字的和是 9,我們可以寫成如下形式
a + 2 a = 9.
為了確定 a 是什麼,讓我們意識到 a + 2a 應該等於 3a。然後,我們可以寫
3a = 9.
所以,a = 3。
由於 a = 3,所以最後兩個數字是 3 和 6。
5)
問題編號 |
數字的和 |
數字的比率 |
數字 |
|
1 |
27 |
2 |
9, 18 |
|
2 |
54 |
2 |
18, 36 |
|
3 |
81 |
2 |
27, 54 |
|
4 |
60 |
2 |
20, 40 |
|
5 |
44 |
3 |
11, 33 |
|
6 |
60 |
3 |
15, 45 |
|
7 |
400 |
3 |
100, 300 |
|
8 |
60 |
4 |
12, 48 |
模式:較小的數字 = (數字的和) / (1 + 數字的比率)
6) 現在,檢視下面這些問題的解題方法。
問題編號 |
各位數字之和 |
比率 |
找出這些數字 |
1 |
45 |
4 |
2, 8 |
2 |
52 |
2 |
1, 2 |
3 |
43 |
2 |
4, 8 |
4 |
40 |
2 |
5, 10 |
7) 較小的數字 = (55 - 和) / (1 + 比率)
8) 9x9 數獨謎題
問題編號 |
各位數字之和 |
比率 |
找出這些數字 |
1 |
41 |
3 |
1, 3 |
2 |
33 |
2 |
4, 8 |
3 |
33 |
3 |
3, 9 |
4 |
30 |
2 |
5, 10 |
9) 較小的數字 = (45 - 和) / (1 + 比率)
下面,我們開發一個公式來確定兩個數字,其中兩個數字的比率為 r ,兩個數字的和為 b。
設這兩個數字為 a 和 r * a。
我們可以寫 a + r * a = b。
解決這個問題,我們將得到 a = b / (1 + r)。
現在,我們知道一個數字是 a。第二個數字將是 r * a。
===探索乘積和商===
練習
- 已知 xy = 8 且 x/y = 2,那麼 x 是多少,y 是多少?
- 根據第一兩列中 x、y 的乘積和比率找到 x 和 y。
x & y 的乘積 |
x & y 的比率 |
x |
y |
4 |
1 |
||
9 |
1 |
||
16 |
1 |
||
8 |
2 |
||
18 |
2 |
||
3 |
3 |
||
12 |
3 |
- 找出下表中的模式。
x & y 的乘積 |
x & y 的比率 |
x |
y |
4 |
1 |
2 |
2 |
9 |
1 |
3 |
3 |
16 |
1 |
4 |
4 |
8 |
2 |
4 |
2 |
18 |
2 |
6 |
3 |
3 |
3 |
3 |
1 |
12 |
3 |
6 |
2 |
解答
(1) 由於 x/y = 2,所以 x 是 y 的兩倍。我們將建立一個 x 是 y 的兩倍的 x 和 y 可能值的表格。
y |
x |
xy |
1 |
2 |
2 |
2 |
4 |
8 |
3 |
6 |
18 |
查看錶格,我們可以得出結論,y = 2 且 x = 4。
(2)
x & y 的乘積 |
x & y 的比率 |
x |
y |
4 |
1 |
2 |
2 |
9 |
1 |
3 |
3 |
16 |
1 |
4 |
4 |
8 |
2 |
4 |
2 |
18 |
2 |
6 |
3 |
3 |
3 |
3 |
1 |
12 |
3 |
6 |
2 |
(3) 找出下表中的模式
x & y 的乘積 |
x & y 的比率 |
x |
y |
4 |
1 |
2 |
2 |
9 |
1 |
3 |
3 |
16 |
1 |
4 |
4 |
8 |
2 |
4 |
2 |
18 |
2 |
6 |
3 |
3 |
3 |
3 |
1 |
12 |
3 |
6 |
2 |
人們可能會觀察到各種模式:隨著乘積的增加而比率保持不變,x 增加而 y 也增加。
比率和乘積的乘積是 x 的平方。乘積除以比率是 y 的平方。
相關謎題:數獨、數獨變體、數獨謎題
練習
- 我有四個數字:2、3、4 和 6。我可以用多少種方法將它們放在一行四個方格中?
- 在 6x6 的數獨謎題的第一行中考慮兩個 2 方格的籠子。{2, 3, 4, 6} 中的每個數字最多隻能在這些籠子中出現一次,因為 1 和 5 已經被分配到該行中剩餘的方格中。一個籠子的目標是 12x。另一個籠子的目標是 1-。1- 籠子中有哪些數字?
答案
- 在四個方格中放置數字的方法有 4 x 3 x 2 x 1 = 24 種。
- 對於目標為 12x 的籠子,有兩種可能性 (C1:2, 6 C2:3, 4)。對於目標為 1- 的籠子,有兩種可能性 (B1:2, 3 B2:3, 4)。綜合考慮所有可能的情況,只有一種可能性與目標數字一致。這對應於 C2 和 B2:12x 籠子中的 2 和 6 以及 1- 籠子中的 3 和 4。
籠子 1 |
籠子 2 |
每個數字使用一次 |
C1 3, 4 |
B1 2, 3 |
否 |
C1 3, 4 |
B2 3, 4 |
否 |
C2 2, 6 |
B1 2, 3 |
否 |
C2 2, 6 |
B2 3, 4 |
是 |
考慮以下問題
我有一組十個數。在這組數中,數字 1 到 10 每個都出現一次,但不一定按升序排列。前七個數的和為 39。第八個數是 7。最後兩個數的比率為 2。最後兩個數是什麼?
假設參與比率的較小數字是 a。現在,數字 1 到 10 的總和是 55。所以,如果我從 a 開始,加上它的兩倍,然後加上 39,最後再加 7,結果將是 55。
你可以在這裡使用的一種策略是逆向工作。讓我們用圖表描述一下我們所描述的內容
為了逆向工作,我們嘗試先確定 C。
由於 C + 7 = 55 且逆運算為 C = 55 - 7 = 48。
現在,我們將嘗試確定 B。
由於 B + 39 = 48 且逆運算為 B = 48-39 = 9。
最後,我們將嘗試確定 A。
由於 A 乘以 3 是 9 且乘法的逆運算為除法,所以 A 是 9 除以 3 = 3。
練習
- 我從一個數字開始。我把它乘以 4。我加上 20。我減去 8。我得到 20。我一開始的數字是多少?
- 我從一個數字開始。我把它乘以 4。我加上 20。我減去 8。我得到 24。我一開始的數字是多少?
- 我從一個數字開始。我把它乘以 4。我加上 20。我減去 8。我得到 28。我一開始的數字是多少?
- 我從一個數字開始。我加上 10。我乘以 2。我加上 2。結果是 26。我一開始的數字是多少?
- 我從一個數字開始。我加上 12。我乘以 2。我加上 2。結果是 32。我一開始的數字是多少?
解答
(1) 2 (2) 3 (3) 4 (4) 2 (5) 3
相關謎題:殺手數獨、肯肯
在之前的一些探索中(和差),我們發現知道從 1 到謎題中允許的最大數字的總和很有用。
練習
(1) 找出下表中列出的第一行中的一組數字和第二行中這些數字的總和的模式。
1 到 2 |
1 到 3 |
1 到 4 |
1 到 5 |
1 到 6 |
1 到 7 |
1 到 8 |
1 到 9 |
1 到 10 |
3 |
6 |
10 |
15 |
21 |
28 |
36 |
45 |
55 |
解答
(1) 尋找模式的一個好策略是檢查差異。
|
差別 |
1 |
1 |
1 |
1 |
1 |
1 |
1 | ||
|
差別 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 | |
3 |
6 |
10 |
15 |
21 |
28 |
36 |
45 |
55 | |
1, 2 |
1–3 |
1–4 |
1–5 |
1–6 |
1–7 |
1–8 |
1–9 |
1–10 |
另一個需要記住的規則是:當二級差為常數時,數字與 n * n 的平方相關,其中 n 是該數字在序列中的位置。所以,讓我們透過在下表中尋找模式來檢查這些數字。
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 | |
|
n |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
n x n |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
100 |
|
和 |
3 |
6 |
10 |
15 |
21 |
28 |
36 |
45 |
55 |
經過一番試驗後,我們會發現底層模式是和 = (n x n + n) / 2。
讓我們檢查一下和。
1+ 2 + 3 … + 20。
獲得此和答案的一種方法是使用上面提到的公式 (20 x 20 + 20) / 2 = 210。
另一種方法是將第一個數字和最後一個數字配對,將第二個數字和倒數第二個數字配對,依此類推。在每種情況下,總和都為 21。現在,讓我們確定有多少對數字。有十對。因此,總和將是 21 x 10 = 210。
在算術數列中,一項與下一項之間的差是一個常數。例如,1、4、7、10、13、16、19、22、25。一般來說,你可以這樣寫一個算術數列
{a, a + d, a + 2d, a + 3d, ... }
其中
• a 是第一項,並且
• d 是各項之間的差(稱為“公差”。
考慮以下關於算術數列的問題:求 1 + 3 + 5 + … 49 的和。
這裡,我們可以將第一個數和最後一個數配對,第二個數和倒數第二個數配對,依此類推。我們有十二對這樣的數,它們加起來都等於 50。中間的數是 25,它本身就是一個數。所以,總和將是 12 x 50 + 25 = 625。
算術數列的公式如下
a + (a + d) + (a + 2d) + (a + 3d) + ...(a + (n - 1) d) = n/ 2 (a + a + (n - 1) d).
總結反思
參考文獻
美國數學教師委員會。學校數學的原則和標準。2000 年。
Beneduct Carey。追蹤創造性解決問題的火花。紐約時報。2010 年 12 月 6 日。
Gordon,Peter。Mensa 數獨解題指南:數百個難題加上幫助你破解所有難題的技術。斯特林。2006 年。
John Kounios 和 Mark Beeman。Aha!時刻 頓悟的認知神經科學。在心理學當前方向。2012 年。
Kulkarni,D。享受數學:透過 KenKen 謎題學習解決問題。休閒數學出版物。2012 年。
Lenchner,G。學校數學中的創造性問題解決,霍頓·米夫林 1983 年。
Mason,J。數學思維。皮爾森。1982 年。
Schoen,H。和 Harold,R。透過問題解決教學數學:6-12 年級。美國數學教師委員會。2003 年。
Singmaster,D。休閒數學的不可思議的效用。第一屆歐洲數學大會,巴黎,1992 年 7 月。
Wilson,R。如何解數獨:循序漸進指南。無限創意。2005 年。
附錄
線上謎題資源
[edit | edit source]本書提供了各種基於謎題的課程。但是,它沒有提供大量的謎題集,因為這些謎題很容易以不同的形式(書籍、網站、軟體和應用程式)獲得。本節提供了一個可用資源列表。