跳轉到內容

專家系統/模糊邏輯

Add links
來自華夏公益教科書
一位華夏公益教科書使用者提名此頁面進行清理，因為
最近從維基百科匯入，需要格式化
您可以幫助改進它。請檢視任何相關討論。
一位華夏公益教科書使用者提名此頁面進行清理，因為
最近從維基百科匯入，需要格式化
您可以幫助改進它。請檢視任何相關討論。

此頁面的原始文字改編自維基百科。

關於模糊邏輯

[編輯 | 編輯原始碼]

維基百科在模糊邏輯中有相關資訊

模糊邏輯源於模糊集理論，處理的是近似推理，而不是從經典謂詞邏輯中精確推匯出來的。可以把它看作是模糊集理論的應用方面，處理的是針對複雜問題經過深思熟慮的現實世界專家值（Klir 1997）。

真值程度經常與機率混淆。然而，它們在概念上是不同的；模糊真值代表的是對模糊定義的集合的隸屬關係，而不是對某些事件或條件的可能性。例如，如果一個 100 毫升的玻璃杯中裝有 30 毫升的水，那麼對於兩個模糊集 Empty 和 Full，人們可能會定義這個玻璃杯為 0.7 空和 0.3 滿。請注意，空的概念是主觀的，因此將取決於觀察者或設計者。另一個設計者也可能同樣設計一個集合隸屬函式，其中玻璃杯在所有低於 50 毫升的值時都被認為是滿的。機率設定首先定義玻璃杯的滿度的標量變數，其次，定義條件分佈，描述在給定特定滿度級別的情況下，有人稱玻璃杯為滿的機率。請注意，條件化可以透過隨機選擇玻璃杯標籤的特定觀察者、確定性觀察者的分佈或兩者來實現。雖然模糊邏輯在這種情況中避免談論隨機性，但這種簡化同時掩蓋了“玻璃杯是 0.3 滿”這句話的真正含義。

模糊邏輯允許集合隸屬值在（包含）0 到 1 之間，並且在它的語言形式中，允許像“稍微”、“相當”和“非常”這樣的不精確概念。具體來說，它允許部分屬於一個集合。它與模糊集和可能性理論有關。它由洛特菲·扎德於 1965 年在加州大學伯克利分校提出。

模糊邏輯在某些圈子裡存在爭議，並且被一些控制工程師和大多數認為機率是描述不確定性的唯一嚴格數學方法的統計學家所拒絕。批評者還認為，它不能是普通集合論的超集，因為隸屬函式是根據常規集合定義的。

應用

[編輯 | 編輯原始碼]

模糊邏輯可用於控制家用電器，例如洗衣機（它會感知負載大小和洗滌劑濃度並相應地調整洗滌迴圈）和冰箱。

一個基本的應用可能是描述連續變數的子範圍。例如，用於防抱死制動系統的溫度測量可能具有幾個獨立的隸屬函式，定義了控制制動器正常工作所需的特定溫度範圍。每個函式都將相同的溫度值對映到 0 到 1 範圍內的真值。這些真值可以用來確定如何控制制動器。

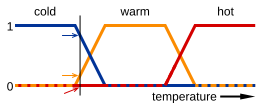
在這張圖片中，冷、溫和熱是將溫度刻度對映到函式的函式。刻度上的一個點具有三個“真值”——每個函式一個。對於用垂直線說明的特定溫度，三個真值可以解釋為描述溫度，例如，“相當冷”（藍色箭頭），“略微溫”（黃色箭頭）和“不熱”（紅色箭頭）。

誤解和爭議

[編輯 | 編輯原始碼]
模糊邏輯與“不精確邏輯”相同。
模糊邏輯並不比任何其他形式的邏輯不精確：它是一種處理固有不精確概念的有組織的數學方法。“寒冷”的概念無法用方程來表達，因為雖然溫度是一個量，但“寒冷”不是。然而，人們對“冷”有一定的概念，並且一致認為，在“冷”和“不冷”之間沒有明確的界限，在那裡某物在 N 度時是“冷的”，但在 N+1 度時是“不冷的”——由於二值原理，經典邏輯難以處理這個概念。結果沒有確定的答案，因此被認為是一個“模糊”的答案。
模糊邏輯是表達機率的一種新方法。
模糊邏輯和機率是表達不確定性的兩種不同方法。雖然模糊邏輯和機率論都可以用來表示主觀信念，但模糊集理論使用的是模糊集隸屬的概念（即變數在多大程度上屬於一個集合），機率論使用的是主觀機率的概念（即我認為變數有多大可能屬於一個集合）。雖然這種區別主要是哲學上的，但模糊邏輯匯出的可能性度量與機率度量本身存在差異，因此它們不直接等效。然而，許多統計學家被布魯諾·德·菲內蒂的工作所說服，認為只需要一種數學不確定性，因此模糊邏輯是不必要的。另一方面，巴特·科斯科認為機率是模糊邏輯的子理論，因為機率只處理一種不確定性。他還聲稱已經證明了從模糊子集概念推匯出貝葉斯定理的推導過程。模糊邏輯的創造者洛特菲·扎德認為，模糊邏輯與機率在性質上是不同的，並不是機率的替代品。他創造了一個模糊的機率替代品，他稱之為可能性理論。其他有爭議的不確定性方法包括Dempster-Shafer 理論和粗糙集。
模糊邏輯將難以擴充套件到更大的問題。
這種批評主要是由於條件可能性（模糊集理論中與條件機率等效的概念）存在問題（參見 Halpen (2003)，第 3.8 節）。這使得推斷變得困難。然而，很少有研究比較基於模糊的系統和機率系統。

模糊邏輯應用的例子

[編輯 | 編輯原始碼]
  • 汽車和其他車輛子系統，例如自動變速器、ABS 和巡航控制（例如東京單軌鐵路）
  • 空調
  • 《指環王》電影中使用的龐大引擎，幫助展示了規模巨大的軍隊創造出隨機但有序的運動
  • 相機
  • 數字影像處理，例如邊緣檢測
  • 電飯煲
  • 洗碗機
  • 電梯
  • 洗衣機和其他家用電器
  • 電子遊戲人工智慧
  • 論壇和聊天室中的語言過濾器，用於過濾掉攻擊性文字
  • 遙感中的模式識別
  • 模糊邏輯也已被整合到一些微控制器和微處理器中，例如飛思卡爾 68HC12。

模糊邏輯的應用

[編輯 | 編輯原始碼]

模糊集理論定義了模糊集上的模糊運算子。應用此方法的問題在於可能不知道適當的模糊運算子。出於這個原因，模糊邏輯通常使用 IF/THEN 規則，或等效的結構，例如模糊關聯矩陣。

規則通常以以下形式表達
IF 變數 IS 集合 THEN 動作

例如，一個非常簡單的使用風扇的溫度調節器可能如下所示
IF 溫度 IS 非常冷 THEN 停止風扇
IF 溫度 IS 冷 THEN 降低風扇速度
IF 溫度 IS 正常 THEN 維持水平
IF 溫度 IS 熱 THEN 加快風扇速度

請注意，沒有“ELSE”。所有規則都會被評估，因為溫度可能同時“冷”和“正常”，但程度不同。

布林邏輯的 AND、OR 和 NOT 運算子存在於模糊邏輯中，通常定義為最小值、最大值和補集；當它們以這種方式定義時，它們被稱為扎德運算子，因為它們最初是在扎德的原始論文中這樣定義的。所以對於模糊變數 x 和 y

NOT x = (1 - truth(x))

x AND y = minimum(truth(x), truth(y))

x OR y = maximum(truth(x), truth(y))

還有一些其他運算子，它們在本質上更具語言性，被稱為修飾符，可以應用於它們。這些通常是副詞，例如“非常”或“有點”，它們使用數學公式來修改集合的含義。

在應用中，Prolog 程式語言非常適合實現模糊邏輯，因為它提供了建立“規則”資料庫的功能，這些規則可以被查詢以推斷邏輯。這種型別的程式設計被稱為邏輯程式設計。

一旦定義了模糊關係，就可以開發模糊關係資料庫。第一個模糊關係資料庫 FRDB 出現在 Maria Zemankova 的論文中。之後，出現了一些其他模型，例如 Buckles-Petry 模型、Prade-Testemale 模型、Umano-Fukami 模型或 J.M. Medina、M.A. Vila 等人的 GEFRED 模型。在模糊資料庫的背景下，已經定義了一些模糊查詢語言，突出顯示了 P. Bosc 等人的 SQLf 和 J. Galindo 等人的 FSQL。這些語言定義了一些結構，以便在 SQL 語句中包含模糊方面，例如模糊條件、模糊比較器、模糊常量、模糊約束、模糊閾值、語言標籤等等。

其他示例

[編輯 | 編輯原始碼]
  • 如果一個男人身高 1.8 米，則認為他很高。

如果男性為真 且 身高 >= 1.8 那麼 is_tall 為真；is_short 為假。

  • 模糊規則不會在高和矮之間進行嚴格區分，這不是很現實。

如果身高 <= 中等男性 那麼 is_short 為有點同意。
如果身高 >= 中等男性 那麼 is_tall 為有點同意。

在模糊情況下，不存在 1.83 米這樣的高度，但存在模糊值，例如以下分配

矮個子男性 = [0, 1.3] 米
個子男性 = (1.3, 1.5]
中等男性 = (1.5, 1.8]
高個子男性 = (1.8, 2.0]
巨人男性 > 2.0 米

對於結果，也不只有兩個值，而是五個，例如

不同意 = 0
有點同意 = 1
有點同意 = 2
非常同意 = 3
完全同意 = 4

在二進位制或“清晰”的情況下，身高為 1.79 米的人被認為是矮個子。如果另一個人身高為 1.8 米或 2.25 米，則這些人被認為是高個子。

清晰的示例有意與模糊的示例不同。我們沒有在前提中放入

如果男性 >= 有點同意 並且 ...

因為性別通常被認為是二元資訊。所以，它不像身高那樣複雜。


形式化模糊邏輯

[編輯 | 編輯原始碼]

在數學邏輯中，有幾個形式系統對上述“模糊邏輯”的概念進行建模；它們大多數屬於所謂的 t-範數模糊邏輯。請注意，它們使用與上面提到的扎德運算子不同的運算子集。

命題模糊邏輯

[編輯 | 編輯原始碼]

最重要的命題模糊邏輯是

  • 基本命題模糊邏輯 BL 是一個邏輯公理化，其中合取由連續的 |t-範數定義，蘊涵由 t-範數的殘差定義。它的模型對應於 BL-代數。
  • Łukasiewicz 模糊邏輯是基本模糊邏輯的一個特例，其中合取是 Łukasiewicz t-範數。它具有基本邏輯的公理，再加上雙重否定公理（因此它不是直覺邏輯），它的模型對應於 MV-代數。
  • Gödel 模糊邏輯是基本模糊邏輯的一個特例，其中合取是 Gödel t-範數。它具有基本邏輯的公理，再加上合取冪等公理，它的模型被稱為 G-代數。
  • 乘積模糊邏輯是基本模糊邏輯的一個特例，其中合取是乘積 t-範數。它具有基本邏輯的公理，再加上另一個公理，它的模型被稱為乘積代數。
  • 單調 t-範數邏輯 MTL 是基本模糊邏輯 BL 的一個泛化，其中合取由左連續的 t-範數實現。它的模型（MTL-代數）是預線性交換有界積分殘差格。
  • 有理 Pavelka 邏輯是多值邏輯的泛化。它是 Łukasiewicz 模糊邏輯的擴充套件，包含額外的常量。

所有這些邏輯都包含傳統的命題邏輯（它的模型對應於布林代數）。

謂詞模糊邏輯

[編輯 | 編輯原始碼]

這些透過新增全稱量詞和存在量詞來擴充套件上述模糊邏輯，類似於謂詞邏輯從命題邏輯中建立的方式。t-範數模糊邏輯中全稱量詞和存在量詞的語義分別是量化子公式例項的真值度的下確界和上確界。

模糊邏輯的有效性

[編輯 | 編輯原始碼]

“可判定子集”和“遞迴可列舉子集”的概念是經典數學和經典邏輯的基本概念。然後，就會出現將這些概念適當擴充套件到模糊集理論的問題。E.S. Santos 在模糊圖靈機、馬爾可夫正規模糊演算法和模糊程式的概念上提出了第一個建議。隨後，L. Biacino 和 G. Gerla 提出了以下定義，其中Ü 表示 [0,1] 中的有理數集。一個集合S 的模糊子集 μ : S [0,1]是遞迴可列舉的，如果存在遞迴對映h : S×N Ü 使得對於S 中的每個x，函式h(x,n) 隨著n 的增加而增加，並且 μ(x) = lim h(x,n)。如果 μ 和它的補集 –μ 都是遞迴可列舉的，那麼我們說 μ 是可判定的。G. Gerla 在一篇論文中提出了將這種理論擴充套件到 L-子集的一般情況。提出的定義與模糊邏輯很好地相關。事實上，以下定理成立（只要模糊邏輯的演繹裝置滿足一些明顯的有效性屬性）。

定理。 任何可公理化的模糊理論都是遞迴可列舉的。特別是，儘管有效公式的清晰集通常不是遞迴可列舉的，但邏輯真公式的模糊集是遞迴可列舉的。此外，任何可公理化和完備的理論都是可判定的。

為了支援模糊邏輯的丘奇論題，即模糊子集的遞迴可列舉性概念是合適的，這是一個懸而未決的問題。為此，需要對模糊語法和模糊圖靈機的概念進行進一步研究（例如，參見 Wiedermann 的論文）。另一個懸而未決的問題是從這個概念開始，為模糊邏輯找到 Gödel 定理的擴充套件。

參考書目

[編輯 | 編輯原始碼]
  • Von Altrock, Constantin (1995). 模糊邏輯和神經模糊應用解釋. Upper Saddle River, NJ: Prentice Hall PTR. ISBN 0-13-368465-2.
  • Biacino, L. (2002). "模糊邏輯、連續性和有效性". 數學邏輯檔案. 41 (7): 643–667. doi:10.1007/s001530100128. ISSN 0933-5846. {{cite journal}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
  • Cox, Earl (1994). 模糊系統手冊：構建、使用和維護模糊系統的實踐指南. Boston: AP Professional. ISBN 0-12-194270-8.
  • Elkan, C. (1994). "模糊邏輯的悖論式成功". IEEE Expert. 9 (4): 3–8. doi:10.1109/64.336150. ISSN 0885-9000. {{cite journal}}: 引用中存在空的未知引數：|coauthors= (幫助). 來自 Elkan 的主頁.
  • Gerla, Giangiacomo (2006). "有效性和多值邏輯". Journal of Symbolic Logic. 71 (1): 137–162. ISSN 0022-4812. {{cite journal}}: 引用中存在空的未知引數：|coauthors= (幫助)
  • Hájek, Petr (1998). 模糊邏輯的元數學. 多德雷赫特: 克魯維爾. ISBN 0792352386.
  • Hájek, Petr (1995). "模糊邏輯與算術層次結構". Fuzzy Sets and Systems. 3 (8): 359–363. doi:10.1016/0165-0114(94)00299-M. ISSN 0165-0114. {{cite journal}}: 引用中存在空的未知引數：|coauthors= (幫助)
  • Halpern, Joseph Y. (2003). 關於不確定性的推理. 馬薩諸塞州劍橋: 麻省理工學院出版社. ISBN 0-262-08320-5.
  • Höppner, Frank (1999). 模糊聚類分析：分類、資料分析和影像識別方法. 紐約: 約翰·威利. ISBN 0-471-98864-2. {{cite book}}: 未知引數 |coauthors= 被忽略 (|author= 建議) (幫助)
  • Ibrahim, Ahmad M. (1997). 應用模糊電子學導論. 新澤西州恩格伍德峭壁: 普倫蒂斯·霍爾. ISBN 0-13-206400-6. {{cite book}}: 引用中存在空的未知引數：|coauthors= (幫助)
  • Klir, George J. (1988). 模糊集、不確定性和資訊. 新澤西州恩格伍德峭壁: 普倫蒂斯·霍爾. ISBN 0-13-345984-5. {{cite book}}: 未知引數 |coauthors= 被忽略 (|author= 建議) (幫助)
  • Klir, George J. (1997). 模糊集理論：基礎和應用. 新澤西州恩格伍德峭壁: 普倫蒂斯·霍爾. ISBN 0133410587. {{cite book}}: 未知引數 |coauthors= 被忽略 (|author= 建議) (幫助)
  • Klir, George J. (1995). 模糊集和模糊邏輯：理論與應用. 新澤西州上鞍河: 普倫蒂斯·霍爾 PTR. ISBN 0-13-101171-5. {{cite book}}: 未知引數 |coauthors= 被忽略 (|author= 建議) (幫助)
  • Kosko, Bart (1993). 模糊思維：模糊邏輯的新科學. 紐約: 海波里昂. ISBN 0-7868-8021-X.
  • Montagna, F. (2001). "量化模糊邏輯中的三個複雜性問題". Studia Logica. 68 (1): 143–152. doi:10.1023/A:1011958407631. ISSN 0039-3215. {{cite journal}}: 引用中存在空的未知引數：|coauthors= (幫助)
  • Mundici, Daniele (1999). 多值推理的代數基礎. 多德雷赫特: 克魯維爾學術出版社. ISBN 0-7923-6009-5. {{cite book}}: 未知引數 |coauthors= 被忽略 (|author= 建議) (幫助)
  • Novák, Vilém (1999). 模糊邏輯的數學原理. 多德雷赫特: 克魯維爾學術出版社. ISBN 0-7923-8595-0. {{cite book}}: 未知引數 |coauthorsr= 被忽略 (幫助)
  • Passino, Kevin M. (1998). 模糊控制. 波士頓：Addison-Wesley. ISBN 020118074X. {{cite book}}: 未知引數 |coauthors= 被忽略 (|author= 建議) (幫助)
  • Scarpellini, Bruno (1962). "Die Nichaxiomatisierbarkeit des unendlichwertigen Prädikatenkalküls von Łukasiewicz". 符號邏輯雜誌. 27 (2): 159–170. doi:10.2307/2964111. ISSN 0022-4812. {{cite journal}}: 引用包含空未知引數：|coauthors= (幫助)
  • Wiedermann, J. (2004). "Characterizing the super-Turing computing power and efficiency of classical fuzzy Turing machines". Theor. Comput. Sci. 317: 61–69. {{cite journal}}: 引用包含空未知引數：|coauthors= (幫助)
  • Yager, Ronald R. (1994). 模糊建模與控制精要. 紐約：Wiley. ISBN 0-471-01761-2. {{cite book}}: 未知引數 |coauthors= 被忽略 (|author= 建議) (幫助)
  • Zadeh, L.A. (1968). "Fuzzy algorithms". 資訊與控制. 12 (2): 94–102. doi:10.1016/S0019-9958(68)90211-8. ISSN 0019-9958. {{cite journal}}: 引用包含空未知引數：|coauthors= (幫助)
  • Zadeh, L.A. (1965). "Fuzzy sets". 資訊與控制. 8 (3): 338-­353. doi:10.1016/S0019-9958(65)90241-X. ISSN 0019-9958. {{cite journal}}: 引用包含空未知引數：|coauthors= (幫助); |pages= 中位置 5 的軟連字元 (幫助)
  • Zemankova-Leech, M. (1983). "Fuzzy Relational Data Bases". 博士論文. 佛羅里達州立大學. {{cite journal}}: 引用期刊需要 |journal= (幫助)
  • Zimmermann, H. (2001). 模糊集理論及其應用. 波士頓：Kluwer Academic Publishers. ISBN 0-7923-7435-5.
[編輯 | 編輯原始碼]

更多文章

連結頁面

軟體和工具

教程

示例應用

[編輯 | 編輯原始碼]
取自 "https://wikibook.tw/w/index.php?title=Expert_Systems/Fuzzy_Logic&oldid=3233003"
華夏公益教科書