費馬大定理/附錄

本附錄收集了一些證明和深入研究了某些數學概念，這些概念對於深入研究本書的某些方面可能很有趣。它力求保持簡單的方法，但證明是正確的，在某些情況下，有必要藉助一些不直接的概念和段落，這些概念和段落已在可能的情況下進行說明和澄清。

勾股定理

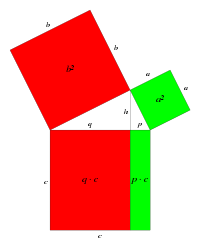
作為數學史上最著名的定理之一，存在著許多證明，包括天文學家、股票經紀人，甚至列奧納多·達·芬奇的證明。也許，它與二次互反律一起，爭奪了具有最多絕對證明的定理的獎項。它將以圖形方式進行證明，僅使用初等幾何的概念。勾股的證明將不予引用，因為它非常複雜，並不直觀。

證明非常簡單，從圖形中可以看出，首先構造一個由四個三角形和兩個正方形組成的正方形，一個邊長為a，另一個邊長為b。正方形的面積是透過將邊乘以自身來計算的，或者用現代符號表示，面積是邊升到二次方。因此，大正方形的面積是a²和b²的平方值之和加上四個三角形的面積之和。在第二個正方形中，我們再次有四個三角形和一個面積為c²的正方形。四個三角形既存在於等式左側，也存在於右側，因此可以消除。因此，等式中剩下

a² + b² = c²

如你所願證明。需要注意的是，證明是通用的，實際上涵蓋了所有可能的直角三角形，因為證明中沒有使用數字，而只使用了通用的線段長度a、b和c。證明僅取決於三角形是直角三角形以及使用的是歐幾里得幾何這一事實。即使如上所述，這個定理有很多幾何證明，這只是一個小型畫廊，實際上還有純粹的代數證明、使用複數的證明，甚至以十四行詩形式寫成的證明。

算術基本定理

算術基本定理指出，每個不等於 1 的自然數都承認唯一的一個素數分解，而不考慮因子的順序。（排除 1 是因為它沒有素數因子。）這個定理是加布裡埃爾·拉梅和奧古斯丁·路易斯·柯西證明的基礎，正如前面所說，它通常不適用於複數，因此不能用於費馬定理，但鑑於它的重要性，決定將其證明包含在附錄中。對於“小”自然數，該語句很容易驗證：很容易發現 70 等於2 × 5 × 7，而 100 等於2 × 2 × 5 × 5 或2² × 5²，此外，很容易驗證對於這些數字，不存在其他素數分解。相反，一般的證明要長得多：這裡摘錄了它的一部分。它處理的是反證法：也就是說，它從與語句相反的假設出發，以便能夠證明它是不成立的。

假設存在某個可以以多種方式分解成素因子的數字，並稱其為最小的m。首先證明，給定m的兩個分解，第一個分解中出現的素數與第二個分解中出現的素數都不相同。事實上，它們是兩個不同的分解

[1]

m=p_{1}p_{2}p_{3}\dots p_{s}

[2]

m=q_{1}q_{2}q_{3}\dots q_{t}

其中p_i和q_j是素數。（注意：在一個分解中，自然地可以存在重複的因子：例如，100 = 2 × 2 × 5 × 5）。如果存在相同的因子p_h = q_k，我們可以用這個因子除以m，得到一個比m小的數字m'，它本身也會有兩種不同的分解。在這一點上，我們知道p₁與q₁不同；不失一般性地，我們可以假設p₁ < q₁。然後我們把

[3]

n=(q_{1}-p_{1})q_{2}q_{3}\dots q_{t}

顯然，n < m，因為[3]可以寫成

[4]

n=q_{1}q_{2}q_{3}\dots q_{t}-p_{1}q_{2}q_{3}\dots q_{t}=m-p_{1}q_{2}q_{3}\dots q_{t}\;\!

.

現在我們證明n至少有兩種不同的分解。我們首先考慮n的第一個因子q₁ - p₁是否可以是素數；如果它不是素數，我們假設對它進行分解。由此得到的n的分解在其因子中不包含p₁。事實上，從證明的第一部分，我們知道p₁與q₂, q₃, ..., q_t不同；但是，它不能出現在q₁ - p₁的最終分解中。事實上，如果這種情況發生，將意味著

q_{1}-p_{1}=p1\cdot b\Rightarrow q_{1}=p_{1}(1+b)

因此，q₁ 可以被 p₁ 整除，但這不可能，因為 q₁ 是一個質數。現在，我們用 [1] 中的值替換 [4] 中的 m，得到

[5]

n=p_{1}p_{2}p_{3}\dots p_{s}-p_{1}q_{2}q_{3}\dots q_{t}\rightarrow n=p_{1}(p_{2}p_{3}\dots p_{s}-q_{2}q_{3}\dots q_{t})

無論 [5] 中第二個因子的分解方式如何，我們都將得到一個包含 p₁ 的 n 的分解，因此它與 [3] 中的分解不同，這與 m 是唯一一個具有多種分解方式的最小數的假設相矛盾。因此定理得證。

歸納原理

歸納原理指出：

如果 $U$ 是自然數集 $\mathbb {N}$ 的一個子集，並且滿足以下兩個性質：

$U$ 包含 $0$ ,

每當 $U$ 包含一個數 $n$ 時， $U$ 也包含其後繼數 $n+1$ ,

那麼 $U$ 與所有自然數集 $\mathbb {N}$ 重合。

這通常在 Peano 公理中找到，併為數學各個領域中的證明提供了強有力的工具。由於許多數學家試圖證明費馬大定理的基準情況，然後將解推廣到包括後續情況，因此在本書中，我們偶爾會回顧這個原理。

歸納法證明

為了證明一個包含自然數 $n$ 的斷言 $P(n)$ 對所有 $n\in \mathbb {N}$ 有效，我們需要用以下方式使用歸納原理：

我們設 $U=\{n\in \mathbb {N} :{\mbox{vale }}P(n)\}$ ,

首先，證明 $P(0)$ 是有效的，也就是說 $0$ 屬於自然數集 $U$ ，對於該集合中的所有 $n$ ，命題 $P(n)$ 是有效的；
假設命題 $P(n)$ 對於任意一個 $n$ 是有效的，並從這個假設出發，證明命題 $P(n+1)$ 也是有效的（即 $n\in U\Rightarrow n+1\in U$ ）。

因此，可以得出結論，使得命題 $P(n)$ 有效的數的集合 $U$ 與所有自然數的集合一致。步驟 1 通常被稱為 **歸納基礎**，步驟 2 被稱為 **歸納步驟**。

以下是一種直觀的方式來理解這種型別的證明：如果我們有一個關於基本情況 $P(0)$ 的證明，以及一個關於歸納步驟 $P(n)\Rightarrow P(n+1)$ 的證明，那麼我們顯然可以使用這些證明來證明 $P(1)$ ，方法是在 $P(0)$ （基本情況）和 $P(0)\Rightarrow P(1)$ （它是當 $n=0$ 時歸納步驟的特例）上應用邏輯規則肯定前件，然後我們可以證明 $P(2)$ ，因為我們現在是在 $P(1)$ 和 $P(1)\Rightarrow P(2)$ 上應用肯定前件，因此對於 $P(3)$ ， $P(4)$ ，等等... 此時很明顯，我們可以用有限步（最終會非常長）來產生 $P(n)$ 的證明，對於任何自然數 $n$ ，由此我們推斷出 $P(n)$ 對於每個 $n\in \mathbb {N}$ 都是真的。

一個例子

我們將證明以下公式是有效的

對於每個 $n\in \mathbb {N}$ ： $0+1+2+3+4+...+n={\frac {n(n+1)}{2}}$

在這種情況下，我們有 $P(n)\quad \equiv \quad 0+1+2+3+4+...+n={\frac {n(n+1)}{2}}$ .

歸納基礎: 我們需要證明斷言 $P(n)$ 在 $n=0$ 時為真。因此，代入後，有 $0={\frac {0\cdot 1}{2}}$ ，實際上，這項工作非常簡單，我們只需要進行一個基本的計算。
歸納步驟: 我們需要證明對於任何n，蘊涵關係 $P(n)\Rightarrow P(n+1)$ 是有效的，也就是說，代入後

0+1+2+3+4+...+n={\frac {n(n+1)}{2}}\quad \Rightarrow \quad 0+1+2+3+4+...+n+(n+1)={\frac {(n+1)((n+1)+1)}{2}}

因此，我們需要假設

P(n)\quad \equiv \quad 0+1+2+3+4+...+n={\frac {n(n+1)}{2}}

,

在此等式基礎上進行推導，最終得到與 $n+1$ 類似的等式：例如，我們可以將 $n+1$ 新增到等式P(n)的兩邊

0+1+2+3+4+...+n+(n+1)={\frac {n(n+1)}{2}}+(n+1)

,

然後進行一些簡單的代數運算

0+1+2+3+4+...+n+(n+1)={\frac {n(n+1)}{2}}+{\frac {2(n+1)}{2}}

,

0+1+2+3+4+...+n+(n+1)={\frac {(n+1)(n+2)}{2}}

,

0+1+2+3+4+...+n+(n+1)={\frac {(n+1)((n+1)+1)}{2}}

而這個最終等式正是 $P(n+1)$ 。這完成了歸納步驟的證明。

因此，在證明了歸納基底和歸納步驟之後，我們可以得出結論（根據歸納原理），對於每一個 $P(n)$ 都必須成立 $n\in \mathbb {N}$ 。 $\square$

模算術

模算術（有時稱為時鐘算術，因為 12 或 24 小時週期內的計算是基於這種原理的）是數學的一個重要分支。它在密碼學、數論（特別是素數的研究）中有著廣泛的應用，也是許多最常見的算術和代數運算的基礎。它處理一個整數算術系統，在這個系統中，數字每次達到一個特定數字 *n* 的倍數時就會“迴圈自身”，這個特定數字 *n* 被稱為模數。模算術是由卡爾·弗里德里希·高斯在他的著作《算術研究》中正式引入的，該書於 1801 年出版。模算術基於 **模 *n* 同餘** 的概念。給定三個整數 *a*、*b*、*n*，其中 *n*≠0，我們說 *a* 和 *b* 模 *n* 同餘，如果它們的差（*a−b*）是 *n* 的倍數。在這種情況下，我們寫