金融數學 FM/期權策略

在金融中，期權策略是指購買和/或出售一個或多個期權頭寸，以及可能包含基礎頭寸。

期權策略可以有利於基礎資產的看漲、看跌或中性走勢。在中性策略的情況下，它們可以進一步分類為看漲波動率和看跌波動率。使用的期權頭寸可以是看漲和/或看跌期權的多頭和/或空頭頭寸，並在各種執行價格。

方向性策略

看漲期權策略是在期權交易者預計基礎股票價格會上漲時採用的。看跌期權策略是看漲策略的映象。它們是在期權交易者預計基礎股票價格會下跌時採用的。

價差

看漲期權價差

看漲期權價差是透過購買執行價格較低（K）的看漲期權，並賣出執行價格較高的另一份看漲期權來構建的。

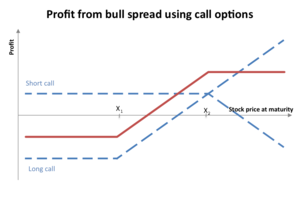
通常執行價格較低的看漲期權將處於平值，而執行價格較高的看漲期權將處於虛值。兩種看漲期權必須具有相同的基礎證券和到期月份。

例子

以任意股票 XYZ 為例，其當前價格為 100 美元。此外，假設它是一個標準期權，這意味著每個期權合約控制 100 股。

假設在下個月，執行價格為 100 美元的看漲期權的價格為每股 3 美元，即每份合約 300 美元，而執行價格為 115 美元的看漲期權的價格為每股 1 美元，即每份合約 100 美元。

然後，交易者可以以 300 美元的價格買入 100 美元執行價格期權的多頭頭寸，並以 100 美元的價格賣出 115 美元期權的空頭頭寸。該交易的淨借方然後是 $300 - 100 = $200。

如果股票在到期時收盤價高於 102 美元，則該交易將產生盈利。如果股票在到期時的收盤價為 110 美元，則 100 美元看漲期權將在到期時為每股 10 美元，即每份合約 1000 美元，而 115 美元看漲期權將到期無效。因此總利潤為 $1000 - 200 = $800。

該交易的利潤限制在每股 13 美元，即執行價格差減去淨借方 (15 - 2)。交易中可能的最大損失等於每股 2 美元，即淨借方。

看跌期權價差

看跌期權價差是透過賣出更高執行價格的實值看跌期權，並買入相同數量的更低執行價格的實值看跌期權來構建的，它們具有相同的基礎證券和到期日期。採用這種策略的期權交易者希望基礎證券的價格上漲足夠多，以致賣出的看跌期權到期無效。

例子

以任意股票 ABC 為例，其當前價格為 100 美元。此外，再次假設它是一個標準期權，這意味著每個期權合約控制 100 股。

假設在下個月，執行價格為 105 美元的看跌期權的價格為每股 8 美元，即每份合約 800 美元，而執行價格為 125 美元的看跌期權的價格為每股 27 美元，即每份合約 2700 美元。

然後，交易者可以以 800 美元的價格開立 105 美元執行價格看跌期權的多頭頭寸，並以 2700 美元的價格開立 125 美元看跌期權的空頭頭寸。該交易的淨貸方然後是 $2700 - 800 = $1900。

如果股票在到期時收盤價高於 106 美元，則該交易將產生盈利。如果股票在到期時的收盤價為 110 美元，則 105 美元看跌期權將到期無效，而 125 美元看跌期權將在到期時為每股 15 美元，即每份合約 1500 美元。因此總利潤為 $1900 - 1500 = $400。

該交易的利潤限制在每股 19 美元，等於淨貸方。交易中可能的最大損失為每股 1 美元，即執行價格差減去淨貸方 (20 - 19)。

中性或非方向性策略

期權交易中的中性策略是在期權交易者不知道基礎股票價格會上漲還是下跌時採用的。它們也被稱為非方向性策略，之所以這麼命名是因為盈利潛力並不取決於基礎股票價格會上漲還是下跌。相反，要採用的正確中性策略取決於基礎股票價格的預期波動率。

中性策略的例子是

裸跨式 - 賣出實值看跌和看漲期權
蝶式 - 買入實值和虛值看漲期權，賣出兩份平值看漲期權，反之亦然
跨式 - 持有相同執行價格和到期日的看漲和看跌期權頭寸。如果期權是買入的，持有者就擁有看漲跨式。如果期權是賣出的，持有者就擁有看跌跨式。看漲跨式在基礎股票價值發生重大變化時（無論上漲還是下跌）都有利可圖。看跌跨式在沒有這種重大變化時有利可圖。
跨式 - 同時買入或賣出虛值看跌期權和虛值看漲期權，它們具有相同的到期日期。與跨式類似，但執行價格不同。
風險反轉

看漲波動率

當基礎股票價格出現大幅上漲或下跌時，看漲波動率的中性交易策略就會獲利。它們包括看漲跨式、看漲寬跨式、看跌翼展和看跌蝶式。

看跌波動率

當基礎股票價格出現微小變化或沒有變化時，看跌波動率的中性交易策略就會獲利。這些策略包括看跌跨式、看跌寬跨式、比率價差、看漲翼展和看漲蝶式。

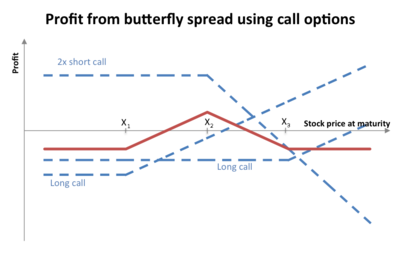
在金融領域，蝴蝶是一種有限風險、非方向性的期權策略，其設計目的是在標的未來波動率預計與隱含波動率不同時，以較高的機率賺取少量有限的利潤。

看漲蝴蝶

如果未來波動率低於隱含波動率，看漲蝴蝶倉位將獲利。

看漲蝴蝶期權策略包括以下期權：

買入 1 個行權價為 (X − a) 的看漲期權
賣出 2 個行權價為 X 的看漲期權
買入 1 個行權價為 (X + a) 的看漲期權

其中 X = 現貨價格，a > 0。

使用看漲期權 - 看跌期權平價關係，看漲蝴蝶也可以透過以下方式構建：

買入 1 個行權價為 (X + a) 的看跌期權
賣出 2 個行權價為 X 的看跌期權
買入 1 個行權價為 (X − a) 的看跌期權

其中 X = 現貨價格，a > 0。

所有期權的到期日相同。

到期時，蝴蝶的價值（但不是利潤）將為：

如果標的的價格低於 (X − a) 或高於 (X + a)，則為零
如果標的的價格介於 (X - a) 和 (X + a) 之間，則為正

最大值出現在 X 處（見圖）。

看跌蝴蝶

如果未來波動率高於隱含波動率，看跌蝴蝶倉位將獲利。

看跌蝴蝶期權策略與看漲蝴蝶相同。但是，所有看漲期權倉位都是賣出，所有看跌期權倉位都是買入。

蝴蝶的變體

中間的雙期權倉位稱為主體，而另外兩個倉位稱為翅膀。

中間兩個倉位的行權價不同的期權策略被稱為鐵凝固。

在非對稱蝴蝶中，變數 "a" 有兩個不同的值。

參考文獻

McMillan, Lawrence G. (2002). 期權作為戰略性投資 (第 4 版)。紐約：紐約金融學院。 ISBN 0-7352-0197-8. {{cite book}}: |edition= has extra text (help)

外部連結

蝴蝶篩選器
看漲和看跌蝴蝶以圖形方式說明了看漲和看跌蝴蝶中的組成期權。
蝴蝶價差 - 展開你的翅膀，獲取利潤關於蝴蝶價差的你需要知道的事情。
- 瞭解有關蝴蝶期權交易策略的更多資訊透過真實的交易示例。

參考文獻

McMillan, Lawrence G. (2002). 期權作為戰略性投資 (第 4 版)。普林斯頓大學出版社。 ISBN 0-7352-0197-8. {{cite book}}: |edition= has extra text (help)

外部連結