流體力學應用/A07 高爾夫球上的凹坑

事實上，人們注意到表面積的斷裂會減少物體後面形成的渦流。例如，為了減少汽車上的阻力，會引入擾流板。高爾夫球上的凹坑也起著類似的作用，但還有許多其他用途。高爾夫球上的凹坑決定了高爾夫球的飛行、軌跡和運動。基本上，這一切都取決於球的空氣動力學。正如我們所知，有兩種型別的流動，即層流和湍流。層流最初經歷的阻力較小，但它也容易分離（邊界層現象）。由於這種現象，阻力隨時間增加。但在湍流的情況下則相反。事實上，這些凹坑會在球體旁邊的空氣層中產生湍流。從而減少阻力。

高爾夫球的歷史

一開始，高爾夫球是用皮革製成的，用溼鵝毛摩擦。這些球被稱為“羽毛球”。隨著時間的推移，人們開始用模製橡膠汁液製造球。這些球被稱為“古塔膠球”，因為它們是用古塔膠樹的汁液製成的。這些球的設計成完美的球形，因為人們認為光滑的球會飛得更遠，阻力更小。但當高爾夫球手發現那些被擊打出凹痕、凸起和切片的球飛得更遠時，這個想法被證明是錯誤的。這是因為凹痕和切口充當了球體表面的分流器。因此，在 1930 年，人們偶然發現了凹坑高爾夫球，從那時起，凹坑高爾夫球就被一直使用著。高爾夫球上的凹坑數量沒有限制，但通常是 300 到 500 個。392 個凹坑被廣泛使用，因為這種型別的球可以讓高爾夫球手獲得滿意的結果。此後，人們認為凹坑數量越多，球飛得越遠，但這個理論被否定了。但是，製造商嘗試了各種凹坑組合和數量。現在，市面上有很多種凹坑的高爾夫球。有些很深，有些很淺，還有大和小。凹坑的形狀也有所不同。它們可能是圓形、橢圓形，甚至六邊形。

這張圖片顯示了高爾夫球和光滑球的差異

凹坑的優勢

高爾夫球上的凹坑有許多優勢。它們是

• 凹坑將高爾夫球的自旋轉化為升力。這是偶然發現的。
• 凹坑減少了施加在球上的阻力。凹坑球的阻力大約是光滑球的一半。
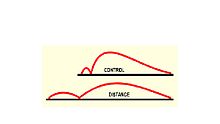
• 高爾夫球上凹坑的數量和大小決定了高爾夫球的軌跡或飛行特性。例如，“距離球”的設計目的是讓球低飛，反彈更遠，這在長球道或逆風情況下有利。但在短球道上，則使用“控制球”。這些球的凹坑設計目的是在球弧末端產生升力，使球幾乎垂直下降。
• 凹坑會在球體周圍的空氣層中產生湍流。這會導致更小的渦流。

球的不同軌跡

升力和阻力的力學

這幅圖描繪了施加在高爾夫球上的各種力。這些力包括阻力、重力和馬格努斯力。

當高爾夫球在空中飛行時，有三種力作用在它上面。其中兩種很容易分析，分別是重力和阻力。還有一種力作用在它上面，它是由於馬格努斯效應產生的，稱為馬格努斯力。這種力是由於球的自旋產生的。最初人們認為，完美的球形球體且表面光滑的球會經歷更小的阻力，但事實並非如此。如果球沒有自旋，這種感知可能是正確的，但實際情況表明，球在離開發球檯的瞬間就開始自旋。平均而言，高爾夫球離開發球檯的速度為 80 米/秒，反旋速度約為 60 轉/秒。馬格努斯力是由於球體頂部和底部的邊界處的空氣相對阻力產生的。球體頂部的相對速度比周圍的空氣慢，導致流經球體的空氣的阻力更小。因此，該區域的流動成為層流。類似地，球體底部相對於附近的空氣移動得更快，因此受到透過的空氣的阻力更小。這會在該區域產生湍流層，導致該區域附近的空氣流動相對於球體更慢。因此，伯努利力產生升力，或者我們也可以說，流經球體的流線向下移動，導致球體向上推。根據伯努利方程，${\frac {p}{\rho }}+{\frac {V^{2}}{2}}+gz=constant$

其中，

• $p$-物體上的壓力差
• $\rho$-物體密度
• $V$-包圍物體流體的速度
• $g$-重力加速度
• $z$-物體的高度

因此，凹坑是賦予高爾夫球升力的原因。這是透過在球體周圍產生兩層空氣來實現的。由於頂層的速度比底層快，因此會產生湍流。這減少了阻力，使球飛得比光滑球更遠。

高爾夫球的軌跡

各種凹坑（不同的形狀和大小）也決定了球的飛行特性/軌跡。市面上有各種型別的高爾夫球，由製造商生產。六邊形球具有中等強度，最常使用，使球具有類似於巴克明斯特富勒烯的結構，也有助於高爾夫球手準確地瞭解球的路徑。大多數高爾夫球手需要高爾夫球垂直落下，以便球更容易落入洞中。