“水輪機 ”一詞源於希臘語tyrbē (τύρβη) ,意思是湍流 。水輪機由Gustaf de Laval 於1882年發明。現代水輪機的示範由查爾斯·帕森斯爵士 於1884年發明。水輪機是一種機器,它利用流體的動能,透過設計的機構轉化為機械能 。水輪機由連線到軸上的多個葉片組成,軸通常用來驅動發電機。水輪機的工作原理是,水輪機的葉片被運動的流體(例如蒸汽、水、氣體等)旋轉,從而旋轉連線到使用這種旋轉能量的裝置的軸。
根據水輪機的工作型別,可以將其分為兩種:
上圖是衝擊式水輪機的模型。下圖是反作用式水輪機的模型。 衝擊式水輪機 反作用式水輪機 壓力頭 速度頭 可壓縮流體 不可壓縮流體 在衝擊式水輪機中,首先將所使用的流體透過專門設計的噴嘴 ,將其壓力頭轉化為速度頭 。然後,從噴嘴噴出的所需流體流束撞擊到彎曲的(水桶形狀的 )葉片上。該流體的速度頭因此被用來為旋轉葉片和軸提供動量。葉片的設計方式使得流體從噴嘴撞擊葉片的方向改變其方向並離開葉片。在此過程中產生的衝擊力被用來為葉片提供動量。這就是為什麼我們把這種型別的水輪機稱為衝擊式水輪機 。 衝擊式水輪機最常見的例子是佩爾頓輪
佩爾頓輪是一種水輪機。它是衝擊式水輪機 中最著名的例子。萊斯特·艾倫·佩爾頓在19世紀70年代發明了這種水輪機。這種水輪機利用的是流動的水的能量。早些時候也製造了許多衝擊式水輪機,但它們不像佩爾頓輪那樣高效。這是因為水離開水輪機時仍然帶走了大部分動能,因此能量利用率較低。但是佩爾頓對此進行了研究,並透過改變葉片的幾何形狀找到了一個巧妙的解決方案。它的設計方式使得即使當輪緣的速度等於噴嘴中水的速度的一半時,流出的水也幾乎沒有剩餘能量。這樣,大部分能量都被充分利用了。這使得它成為一種非常高效的水輪機設計。
所需功率可以根據需要進行調節。因此,這種需求可以透過一個矛頭機制來滿足。這可以透過調節矛頭的位置來實現。如果功率需求較高,則將矛頭移向噴嘴的出口,如果功率需求較低,則將矛頭移開噴嘴的出口。因此,功率需求與水流速同步。噴嘴上安裝了一個分流器。特殊的葉片設計使水在 180 o {\displaystyle 180^{o}} 2 n d {\displaystyle 2^{nd}} 180 o {\displaystyle 180^{o}}
最大化能量提取
葉片提取的功率, P = F i m p u l s e × V b u c k e t {\displaystyle P=F_{impulse}\times V_{bucket}}
分析兩種情況
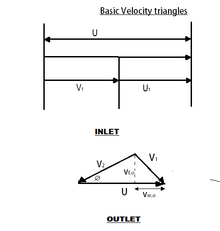
葉片保持靜止 :會產生很大的衝擊力,但由於葉片保持靜止,因此提取的功率為零。葉片的速度與射流速度相同 :如果發生這種情況,則水射流將無法撞擊葉片,導致衝擊力為零。因此,再次沒有能量被提取。入口和出口處的速度三角形 水施加的力= m ˙ ( v w , i − v w , o ) {\displaystyle {\dot {m}}(v_{w,i}-v_{w,o})}
功率= m ˙ ( v w , i − v w , o ) U 1 {\displaystyle {\dot {m}}(v_{w,i}-v_{w,o})U_{1}}
水力效率, η {\displaystyle \eta } ( v w , i − v w , o ) U 1 g U 2 2 g {\displaystyle {(v_{w,i}-v_{w,o}){U_{1} \over g} \over {U^{2} \over 2g}}}
要獲得最大效率,
v w , i = U = V 1 + U 1 {\displaystyle v_{w,i}=U=V_{1}+U_{1}}
v w , o = U 1 − V r , o cos ϕ {\displaystyle v_{w,o}=U_{1}-V_{r,o}\cos {\phi }}
因此, P = m ˙ ( v r , i + v r , o cos ϕ ) {\displaystyle P={\dot {m}}(v_{r,i}+v_{r,o}\cos {\phi })}
假設,葉片沿摩擦阻力=0
( v r , i = v r , o ) {\displaystyle (v_{r,i}=v_{r,o})}
因此, P = m ˙ U 1 ( U − U 1 ) ( 1 + cos ϕ ) {\displaystyle P={\dot {m}}U_{1}(U-U_{1})(1+\cos {\phi })}
為了使P最大化, d P d U 1 = 0 {\displaystyle {\frac {\mathrm {d} P}{\mathrm {d} U_{1}}}=0}
因此, U = 2 U 1 {\displaystyle U=2U_{1}}
Daugherty 對佩爾頓水輪效能的分析
提供給渦輪機的淨水頭h可透過以下公式計算得出:
h = h ″ + k V 2 2 2 g + m V 2 2 2 g + k ″ V 2 2 2 g {\displaystyle h=h''+k{\frac {V_{2}^{2}}{2g}}+m{\frac {V_{2}^{2}}{2g}}+k''{\frac {V_{2}^{2}}{2g}}}
h ″ {\displaystyle h''}
k V 2 2 2 g {\displaystyle k{\frac {V_{2}^{2}}{2g}}}
m V 2 2 2 g {\displaystyle m{\frac {V_{2}^{2}}{2g}}}
k ″ V 2 2 2 g {\displaystyle k''{\frac {V_{2}^{2}}{2g}}}
佩爾頓水斗內水流速度分量的示意圖 轉輪利用的熱量,
h ″ = l g ( u 1 v 1 − u 2 v 2 cos α 2 ) {\displaystyle h''={l \over g}(u_{1}v_{1}-u_{2}v_{2}\cos \alpha _{2})}
利用轉輪中水流相對運動的能量方程。
轉輪內的總水頭損失 = ( z 1 + v 1 2 2 g + p 1 ρ g ) − ( z 2 + v 2 2 2 g + p 2 ρ g ) {\displaystyle ={\Bigg (}z_{1}+{\frac {v_{1}^{2}}{2g}}+{\frac {p_{1}}{\rho g}}{\Bigg )}-{\Bigg (}z_{2}+{\frac {v_{2}^{2}}{2g}}+{\frac {p_{2}}{\rho g}}{\Bigg )}}
利用相對速度和公式 1 & 2,我們得到,
( z 1 + V 1 2 − U 1 2 2 g + p 1 ρ g ) − ( z 2 + V 2 2 − U 2 2 2 g + p 2 ρ g ) {\displaystyle {\Bigg (}z_{1}+{\frac {V_{1}^{2}-U_{1}^{2}}{2g}}+{\frac {p_{1}}{\rho g}}{\Bigg )}-{\Bigg (}z_{2}+{\frac {V_{2}^{2}-U_{2}^{2}}{2g}}+{\frac {p_{2}}{\rho g}}{\Bigg )}}
假設 z 1 = z 2 , p 1 = p 2 , u 1 = u 2 {\displaystyle z_{1}=z_{2},p_{1}=p_{2},u_{1}=u_{2}}
V 2 = V 1 1 + k = v 1 − U 1 1 + k {\displaystyle V_{2}={\frac {V_{1}}{\sqrt {1+k}}}={\frac {v_{1}-U_{1}}{\sqrt {1+k}}}}
水斗上的切向力, F t = m ˙ ( U − u 2 − V 2 cos β ) {\displaystyle F_{t}={\dot {m}}{\bigg (}U-u_{2}-V_{2}\cos \beta {\bigg )}}
F t = m ˙ ( 1 − cos β 2 1 + k ) ( V 1 − U 1 ) {\displaystyle F_{t}={\dot {m}}{\Bigg (}1-{\frac {\cos \beta _{2}}{\sqrt {1+k}}}{\Bigg )}(V_{1}-U_{1})}
P = m ˙ ( 1 − cos β 2 1 + k ) ( V 1 − U 1 ) U 1 {\displaystyle P={\dot {m}}{\Bigg (}1-{\frac {\cos \beta _{2}}{\sqrt {1+k}}}{\Bigg )}(V_{1}-U_{1})U_{1}}
(注意:在實際情況下,不能假設 U = v 1 {\displaystyle U=v_{1}}