GLSL 程式設計/Unity/天光漫反射

一個球形建築，從上方被陰天照亮，從下方被綠色的水池照亮。注意建築物照明不同的顏色。

本教程涵蓋了半球照明。

它基於漫射逐頂點照明，如“漫反射”部分中所述。如果你還沒有閱讀過本教程，你應該先閱讀它。

半球照明基本上是用一個覆蓋場景整個半球的巨大光源計算漫反射照明，例如天空。它通常還包括使用不同的顏色從下方對另一個半球進行照明，因為計算幾乎是免費的。在左側的照片中，球形建築被陰天照亮。然而，周圍的綠色水池也照亮了它，導致建築物下半部分出現明顯的綠色照明。

半球照明

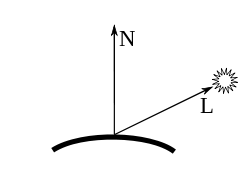
如果我們假設表面上一點周圍的半球上的每個點（方向為L）都充當光源，那麼我們應該透過積分來整合半球上所有點的漫射照明（如“漫反射”部分中所述，由 max(0, L·N) 給出）。讓我們將半球旋轉軸的歸一化方向稱為U（表示“向上”）。如果表面法線N指向U的方向，我們就有完全的照明，顏色由使用者指定。如果它們之間有一個角度 γ（即 cos(γ) = U·N），那麼只有半球的一個球形楔形(參見維基百科文章)會照亮表面點。與完全照明相比，這種照明的分數 w 為

$w={\frac {1}{2}}(1+\cos(\gamma ))$ $={\frac {1}{2}}(1+\mathbf {U} \cdot \mathbf {N} )$

因此，我們可以將入射光計算為 w 乘以使用者指定的半球完全照明的顏色。相反方向的半球將用 1-w 乘以另一種顏色來照亮表面點（如果我們不需要它，它可能是黑色）。下一部分解釋瞭如何推匯出 w 的這個方程。

方程推導

對於任何感興趣的人（以及因為我在網上沒有找到它），這裡是對 w 方程的推導。我們在附著在表面點上的球座標系中對距離為 1 的半球上的照明進行積分，其中N的方向是y軸的方向。如果N和U指向相同的方向，則積分（除了使用者指定的常數顏色之外）為

$\int _{0}^{\pi }\mathrm {d} \phi \int _{0}^{\pi }\mathrm {d} \theta \sin(\theta )\,\mathbf {L} \cdot \mathbf {N} =$ $\int _{0}^{\pi }\mathrm {d} \phi \int _{0}^{\pi }\mathrm {d} \theta \sin(\theta )\left({\begin{array}{c}x\\y\\z\end{array}}\right)\cdot \mathbf {N}$

sin(θ) 是我們在半徑為 1 的球面上積分的雅可比行列式，(x, y, z) 為 (cos(φ)sin(θ), sin(φ)sin(θ), cos(θ))，N = (0,1,0)。因此，積分變為

$\int _{0}^{\pi }\mathrm {d} \phi \int _{0}^{\pi }\mathrm {d} \theta (\sin(\theta ))^{2}\sin(\phi )=\pi$

常數 π 將包含在使用者定義的最大照明顏色中。如果N和U之間存在一個角度 γ，其中 cos(γ) = U·N，那麼積分只在球形楔形（從 γ 到 π）上進行

$w={\frac {1}{\pi }}\int _{\gamma }^{\pi }\mathrm {d} \phi \int _{0}^{\pi }\mathrm {d} \theta (\sin(\theta ))^{2}\sin(\phi )$ $={\frac {1}{2}}(1+\cos(\gamma ))$ $={\frac {1}{2}}(1+\mathbf {U} \cdot \mathbf {N} )$

著色器程式碼

該實現基於 “漫反射” 章節的程式碼。在一個更完善的實現中，其他光源的貢獻也會被包含進來，例如使用 Phong 反射模型，如 “鏡面反射” 章節中所討論的。在這種情況下，半球光照將以與環境光照相同的方式包含在內。

然而，這裡唯一的照光是由於半球光照。w 的方程為

$w={\frac {1}{2}}(1+\mathbf {U} \cdot \mathbf {N} )$

我們在世界空間中實現它，也就是說，我們必須將表面法線向量 N 轉換到世界空間（參見 “世界空間中的著色” 章節），而 U 由使用者在世界空間中指定。我們對向量進行歸一化並計算 w，然後使用 w 和 1-w 來計算基於使用者指定顏色的照亮。實際上，這相當簡單。

Shader "GLSL per-vertex hemisphere lighting" {
   Properties {
      _Color ("Diffuse Material Color", Color) = (1,1,1,1) 
      _UpperHemisphereColor ("Upper Hemisphere Color", Color) 
         = (1,1,1,1) 
      _LowerHemisphereColor ("Lower Hemisphere Color", Color) 
         = (1,1,1,1) 
      _UpVector ("Up Vector", Vector) = (0,1,0,0) 
   }
   SubShader {
      Pass {      
         GLSLPROGRAM
 
         // shader properties specified by users
         uniform vec4 _Color; 
         uniform vec4 _UpperHemisphereColor;
         uniform vec4 _LowerHemisphereColor;
         uniform vec3 _UpVector;
 
         // The following built-in uniforms 
         // are also defined in "UnityCG.glslinc", 
         // i.e. one could #include "UnityCG.glslinc" 
         uniform mat4 _Object2World; // model matrix
         uniform mat4 _World2Object; // inverse model matrix
 
         varying vec4 color; 
            // the hemisphere lighting computed in the vertex shader
 
         #ifdef VERTEX
 
         void main()
         {                                
            mat4 modelMatrix = _Object2World;
            mat4 modelMatrixInverse = _World2Object; // unity_Scale.w 
               // is unnecessary because we normalize vectors
 
            vec3 normalDirection = normalize(vec3(
               vec4(gl_Normal, 0.0) * modelMatrixInverse));
            vec3 upDirection = normalize(_UpVector);
 
            float w = 0.5 * (1.0 + dot(upDirection, normalDirection));
            color = (w * _UpperHemisphereColor 
               + (1.0 - w) * _LowerHemisphereColor) * _Color;
 
            gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
         }
 
         #endif
 
         #ifdef FRAGMENT
 
         void main()
         {
            gl_FragColor = color;
         }
 
         #endif
 
         ENDGLSL
      }
   } 
}

總結

恭喜你完成了另一個教程！我們已經看到了

什麼是半球光照。
半球光照的方程是什麼。
如何實現半球光照。

進一步閱讀

如果你還想了解更多

關於漫反射光照，你應該閱讀 “漫反射” 章節。
關於半球光照，你可以閱讀 Randi Rost 等人於 2009 年由 Addison-Wesley 出版書籍 “OpenGL 著色語言”（第三版）的第 12.1 章。

< GLSL Programming/Unity

除非另有說明，本頁上的所有示例原始碼均授予公有領域。