頂點著色器和之後在 OpenGL (ES) 2.0 管道 中的階段中最重要的一項任務是,將圖元(例如三角形)的頂點從原始座標(例如在 3D 建模工具中指定的座標)變換到螢幕座標。雖然可程式設計的頂點著色器允許以多種方式變換頂點,但一些變換是在頂點著色器後的固定功能階段執行的。因此,在程式設計頂點著色器時,瞭解哪些變換必須在頂點著色器中執行尤為重要。這些變換通常以統一變數的形式指定,並透過矩陣-向量乘法應用於傳入的頂點位置和法向量。雖然對於點和方向來說這是直觀的,但對於法向量來說就不那麼直觀了,如 “應用矩陣變換”部分 中所述。
這裡,我們將首先概述座標系以及它們之間的變換,然後討論各個變換。
相機類比:1. 定位模型,2. 定位相機,3. 調整縮放,4. 裁剪影像 將變換頂點的整個過程想象成一個相機類比,如右圖所示,步驟和相應的頂點變換是
定位模型 - 模型變換
定位相機 - 觀察變換
調整縮放 - 投影變換
裁剪影像 - 視口變換 前三個變換在頂點著色器中應用。然後,透視除法(可能被認為是投影變換的一部分)在頂點著色器後的固定功能階段自動應用。視口變換也在這個固定功能階段自動應用。雖然固定功能階段中的變換不可修改,但其他變換可以被替換為這裡描述的其他型別的變換。然而,瞭解傳統的變換很有用,因為它們可以充分利用裁剪和對變化變數的透視正確插值。
以下概述顯示了不同座標系之間的頂點變換序列,幷包括表示變換的矩陣
物件/模型座標
頂點著色器的輸入,即屬性中的位置
↓
模型變換 :模型矩陣 M object → world {\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}}
世界座標
↓
觀察變換 :觀察矩陣 M world → view {\displaystyle \mathrm {M} _{{\text{world}}\to {\text{view}}}}
觀察/眼睛座標
↓
投影變換 :投影矩陣 M projection {\displaystyle \mathrm {M} _{\text{projection}}}
裁剪座標
頂點著色器的輸出,即 gl_Position
↓
透視除法 (除以 gl_Position.w)
歸一化裝置座標
↓
視口變換
螢幕/視窗座標
片段著色器中的 gl_FragCoord
模型變換指定從物件座標(也稱為模型座標或區域性座標)到公共世界座標系的變換。物件座標通常特定於每個物件或模型,並且通常在 3D 建模工具中指定。另一方面,世界座標是場景中所有物件的公共座標系,包括光源、3D 音訊源等。由於不同的物件具有不同的物件座標系,因此模型變換也不同;即,必須對每個物件應用不同的模型變換。
實際上,它會將物件從原點“推開”,並可以選擇對其應用旋轉。
模型變換可以用一個 4×4 矩陣表示,我們將其表示為模型矩陣 M object → world {\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}}
M object → world = [ a 1 , 1 a 1 , 2 a 1 , 3 t 1 a 2 , 1 a 2 , 2 a 2 , 3 t 2 a 3 , 1 a 3 , 2 a 3 , 3 t 3 0 0 0 1 ] {\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}=\left[{\begin{matrix}a_{1,1}&a_{1,2}&a_{1,3}&t_{1}\\a_{2,1}&a_{2,2}&a_{2,3}&t_{2}\\a_{3,1}&a_{3,2}&a_{3,3}&t_{3}\\0&0&0&1\end{matrix}}\right]} with A = [ a 1 , 1 a 1 , 2 a 1 , 3 a 2 , 1 a 2 , 2 a 2 , 3 a 3 , 1 a 3 , 2 a 3 , 3 ] {\displaystyle {\text{ with }}\mathrm {A} =\left[{\begin{matrix}a_{1,1}&a_{1,2}&a_{1,3}\\a_{2,1}&a_{2,2}&a_{2,3}\\a_{3,1}&a_{3,2}&a_{3,3}\end{matrix}}\right]} and t = [ t 1 t 2 t 3 ] {\displaystyle {\text{ and }}\mathbf {t} =\left[{\begin{matrix}t_{1}\\t_{2}\\t_{3}\end{matrix}}\right]}
A {\displaystyle \mathrm {A} } t 是一個 3D 向量,表示 3D 空間中的平移(即位移)。 M object → world {\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}} A {\displaystyle \mathrm {A} } t 組合在一個方便的 4×4 矩陣中。從數學角度來說,模型矩陣代表仿射變換:線性變換加上平移。為了使這能夠工作,所有三維點都用四維向量表示,第四個座標等於 1。
P = [ p 1 p 2 p 3 1 ] {\displaystyle P=\left[{\begin{matrix}p_{1}\\p_{2}\\p_{3}\\1\end{matrix}}\right]}
當我們將矩陣乘以這樣的點 P {\displaystyle P}
M object → world P = [ a 1 , 1 a 1 , 2 a 1 , 3 t 1 a 2 , 1 a 2 , 2 a 2 , 3 t 2 a 3 , 1 a 3 , 2 a 3 , 3 t 3 0 0 0 1 ] [ p 1 p 2 p 3 1 ] {\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}\;P=\left[{\begin{matrix}a_{1,1}&a_{1,2}&a_{1,3}&t_{1}\\a_{2,1}&a_{2,2}&a_{2,3}&t_{2}\\a_{3,1}&a_{3,2}&a_{3,3}&t_{3}\\0&0&0&1\end{matrix}}\right]\left[{\begin{matrix}p_{1}\\p_{2}\\p_{3}\\1\end{matrix}}\right]} = [ a 1 , 1 p 1 + a 1 , 2 p 2 + a 1 , 3 p 3 + t 1 a 2 , 1 p 1 + a 2 , 2 p 2 + a 2 , 3 p 3 + t 2 a 3 , 1 p 1 + a 3 , 2 p 2 + a 3 , 3 p 3 + t 3 1 ] {\displaystyle =\left[{\begin{matrix}a_{1,1}p_{1}+a_{1,2}p_{2}+a_{1,3}p_{3}+t_{1}\\a_{2,1}p_{1}+a_{2,2}p_{2}+a_{2,3}p_{3}+t_{2}\\a_{3,1}p_{1}+a_{3,2}p_{2}+a_{3,3}p_{3}+t_{3}\\1\end{matrix}}\right]}
除了第四個座標(應該是 1,因為它是點),結果等於
A [ p 1 p 2 p 3 ] + [ t 1 t 2 t 3 ] {\displaystyle \mathrm {A} \left[{\begin{matrix}p_{1}\\p_{2}\\p_{3}\end{matrix}}\right]+\left[{\begin{matrix}t_{1}\\t_{2}\\t_{3}\end{matrix}}\right]}
模型矩陣 M object → world {\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}} gl_ModelViewMatrix。(另見 “應用矩陣變換”部分 。)
嚴格來說,GLSL 程式設計師不必擔心模型矩陣的計算,因為它以統一變數的形式提供給頂點著色器。事實上,渲染引擎、場景圖和遊戲引擎通常會提供模型矩陣;因此,頂點著色器的程式設計師不必擔心計算模型矩陣。然而,在現代版本的 OpenGL 和 OpenGL ES 或 WebGL 中開發應用程式時,必須計算模型矩陣。(OpenGL 3.2 之前的版本、新版本 OpenGL 的相容性配置檔案以及 OpenGL ES 1.x 提供了計算模型矩陣的函式。)
模型矩陣通常透過組合物件的基本變換的 4×4 矩陣來計算,特別是平移、旋轉和縮放。具體來說,在層次場景圖的情況下,物件的父組的所有變換(父、祖父母等)被組合起來形成模型矩陣。讓我們來看看最重要的基本變換及其矩陣。
表示由向量 t = ( t 1 , t 2 , t 3 ) {\displaystyle =(t_{1},t_{2},t_{3})}
M translation = [ 1 0 0 t 1 0 1 0 t 2 0 0 1 t 3 0 0 0 1 ] {\displaystyle \mathrm {M} _{\text{translation}}=\left[{\begin{matrix}1&0&0&t_{1}\\0&1&0&t_{2}\\0&0&1&t_{3}\\0&0&0&1\end{matrix}}\right]}
表示按因子 s x {\displaystyle s_{x}} x {\displaystyle x} s y {\displaystyle s_{y}} y {\displaystyle y} s z {\displaystyle s_{z}} z {\displaystyle z}
M scaling = [ s x 0 0 0 0 s y 0 0 0 0 s z 0 0 0 0 1 ] {\displaystyle \mathrm {M} _{\text{scaling}}=\left[{\begin{matrix}s_{x}&0&0&0\\0&s_{y}&0&0\\0&0&s_{z}&0\\0&0&0&1\end{matrix}}\right]}
表示繞歸一化軸 ( x , y , z ) {\displaystyle (x,y,z)} α {\displaystyle \alpha }
M rotation = [ ( 1 − cos α ) x x + cos α ( 1 − cos α ) x y − z sin α ( 1 − cos α ) z x + y sin α 0 ( 1 − cos α ) x y + z sin α ( 1 − cos α ) y y + cos α ( 1 − cos α ) y z − x sin α 0 ( 1 − cos α ) z x − y sin α ( 1 − cos α ) y z + x sin α ( 1 − cos α ) z z + cos α 0 0 0 0 1 ] {\displaystyle \mathrm {M} _{\text{rotation}}=\left[{\begin{matrix}(1-\cos \alpha )x\,x+\cos \alpha &(1-\cos \alpha )x\,y-z\sin \alpha &(1-\cos \alpha )z\,x+y\sin \alpha &0\\(1-\cos \alpha )x\,y+z\sin \alpha &(1-\cos \alpha )y\,y+\cos \alpha &(1-\cos \alpha )y\,z-x\sin \alpha &0\\(1-\cos \alpha )z\,x-y\sin \alpha &(1-\cos \alpha )y\,z+x\sin \alpha &(1-\cos \alpha )z\,z+\cos \alpha &0\\0&0&0&1\end{matrix}}\right]}
繞特定軸的旋轉的特殊情況可以很容易地推匯出。例如,這些對於實現尤拉角旋轉是必要的。但是,尤拉角有多種約定,這裡不再討論。
歸一化四元數 ( w q , x q , y q , z q ) {\displaystyle (w_{q},x_{q},y_{q},z_{q})} 2 arccos ( w q ) {\displaystyle 2\arccos(w_{q})} ( x q , y q , z q ) {\displaystyle (x_{q},y_{q},z_{q})}
還存在其他基本變換,但對於模型矩陣的計算而言,它們並不那麼重要。這些變換或其他變換的 4×4 矩陣可以透過矩陣乘法來組合。假設矩陣 M 1 {\displaystyle \mathrm {M} _{1}} M 2 {\displaystyle \mathrm {M} _{2}} M 3 {\displaystyle \mathrm {M} _{3}} M 1 {\displaystyle \mathrm {M} _{1}} M 2 {\displaystyle \mathrm {M} _{2}} M 3 {\displaystyle \mathrm {M} _{3}}
M combined = M 3 M 2 M 1 {\displaystyle \mathrm {M} _{\text{combined}}=\mathrm {M} _{3}\mathrm {M} _{2}\mathrm {M} _{1}\,\!}
請注意,矩陣因子的順序很重要。還要注意,此矩陣乘積應從右(向量相乘的地方)到左閱讀,即 M 1 {\displaystyle \mathrm {M} _{1}} M 3 {\displaystyle \mathrm {M} _{3}}
檢視座標系的示意圖。 視點變換對應於放置和定向相機(或觀察者的眼睛)。然而,思考視點變換的最佳方式是它將世界座標轉換為相機的檢視座標系(也稱為眼睛座標系),該相機放置在座標系的原點,指向 **負** z {\displaystyle z} x z {\displaystyle xz} y {\displaystyle y}
此步驟將整個世界旋轉朝向相機,相機始終從原點看向一個固定位置。
與模型變換類似,視點變換由一個 4×4 矩陣表示,稱為檢視矩陣 M world → view {\displaystyle \mathrm {M} _{{\text{world}}\to {\text{view}}}} M object → world {\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}} M object → view {\displaystyle \mathrm {M} _{{\text{object}}\to {\text{view}}}} gl_ModelViewMatrix。)由於模型矩陣首先應用,所以正確的組合是
M object → view = M world → view M object → world {\displaystyle \mathrm {M} _{{\text{object}}\to {\text{view}}}=\mathrm {M} _{{\text{world}}\to {\text{view}}}\mathrm {M} _{{\text{object}}\to {\text{world}}}\,\!}
(另請參閱 “應用矩陣變換”部分 。)
與模型矩陣類似,GLSL 程式設計師不必擔心檢視矩陣的計算,因為它以統一變數的形式提供給頂點著色器。但是,在開發現代版本的 OpenGL 和 OpenGL ES 或 WebGL 中的應用程式時,有必要計算檢視矩陣。(在舊版本的 OpenGL 中,這通常透過一個名為 gluLookAt 的實用程式函式來實現。)
在這裡,我們簡要總結了如何從相機的方位 t 、觀察方向 d 和世界向上向量 k (都在世界座標中)計算檢視矩陣 M world → view {\displaystyle \mathrm {M} _{{\text{world}}\to {\text{view}}}}
1. 計算(在世界座標中)檢視座標系的 z {\displaystyle z} z ,作為負的標準化 d 向量
z = − d | d | {\displaystyle \mathbf {z} =-{\frac {\mathbf {d} }{|\mathbf {d} |}}}
2. 計算(再次在世界座標中)檢視座標系的 x {\displaystyle x} x ,方法是
x = d × k | d × k | {\displaystyle \mathbf {x} ={\frac {\mathbf {d} \times \mathbf {k} }{|\mathbf {d} \times \mathbf {k} |}}}
3. 在世界座標系中計算檢視座標系 y {\displaystyle y} y
y = z × x {\displaystyle \mathbf {y} =\mathbf {z} \times \mathbf {x} }
使用 x 、y 、z 和 t ,可以輕鬆確定逆檢視矩陣 M view → world {\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}} t ,並將單位向量 (1,0,0)、(0,1,0) 和 (0,0,1) 對映到 x 、y, 、z 。因此,後一個向量必須位於矩陣 M view → world {\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}}
M view → world = [ x 1 y 1 z 1 t 1 x 2 y 2 z 2 t 2 x 3 y 3 z 3 t 3 0 0 0 1 ] {\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}=\left[{\begin{matrix}x_{1}&y_{1}&z_{1}&t_{1}\\x_{2}&y_{2}&z_{2}&t_{2}\\x_{3}&y_{3}&z_{3}&t_{3}\\0&0&0&1\end{matrix}}\right]}
但是,我們需要矩陣 M world → view {\displaystyle \mathrm {M} _{{\text{world}}\to {\text{view}}}} M view → world {\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}} M view→world {\displaystyle \mathrm {M} _{\text{view→world}}}
M view → world = [ R t 0 T 1 ] {\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}=\left[{\begin{matrix}\mathrm {R} &\mathbf {t} \\\mathbf {0} ^{T}&1\end{matrix}}\right]}
其中, R {\displaystyle \mathrm {R} } t 是一個 3D 向量。此類矩陣的逆矩陣為
M view → world − 1 = M world → view = [ R − 1 − R − 1 t 0 T 1 ] {\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}^{-1}=\mathrm {M} _{{\text{world}}\to {\text{view}}}=\left[{\begin{matrix}\mathrm {R} ^{-1}&-\mathrm {R} ^{-1}\mathbf {t} \\\mathbf {0} ^{T}&1\end{matrix}}\right]}
由於在此特定情況下矩陣 R {\displaystyle \mathrm {R} } R {\displaystyle \mathrm {R} }
M world → view = [ R T − R T t 0 T 1 ] {\displaystyle \mathrm {M} _{{\text{world}}\to {\text{view}}}=\left[{\begin{matrix}\mathrm {R} ^{T}&-\mathrm {R} ^{T}\mathbf {t} \\\mathbf {0} ^{T}&1\end{matrix}}\right]} with R = [ x 1 y 1 z 1 x 2 y 2 z 2 x 3 y 3 z 3 ] {\displaystyle {\text{with }}\mathrm {R} =\left[{\begin{matrix}x_{1}&y_{1}&z_{1}\\x_{2}&y_{2}&z_{2}\\x_{3}&y_{3}&z_{3}\end{matrix}}\right]}
雖然推導這個結果需要一些線性代數的知識,但最終的計算只需要基本的向量和矩陣運算,並且可以很容易地在任何常見的程式語言中實現。
文藝復興時期的透視畫法:“男人畫魯特琴”由阿爾布雷希特·丟勒,1525年 首先,投影變換決定投影的型別,例如透視投影或正交投影。透視投影對應於具有縮短的線性透視,而正交投影是沒有縮短的正交投影。縮短實際上是透過透視除法完成的;但是,所有控制透視投影的引數都設定在投影變換中。
從技術上講,投影變換將檢視座標轉換為裁剪座標。(場景中可見部分外部的所有圖元部分都在裁剪座標中被裁剪掉。)它應該是頂點著色器中應用於頂點的最後一個變換,在頂點以 gl_Position 返回之前。然後,這些裁剪座標透過**透視除法**轉換為歸一化裝置座標,該除法只是將所有座標除以第四個座標。(歸一化裝置座標之所以如此命名,是因為它們的取值範圍在場景中可見部分的所有點的 -1 到 +1 之間。)
此步驟將物體頂點的 3D 位置轉換為螢幕上的 2D 位置。
與模型變換和檢視變換類似,投影變換由一個 4×4 矩陣表示,稱為投影矩陣 M projection {\displaystyle \mathrm {M} _{\text{projection}}} gl_Projection;另請參見“應用矩陣變換”部分 。)
與模型檢視矩陣類似,GLSL 程式設計師不必擔心投影矩陣的計算。但是,在現代版本的 OpenGL 和 OpenGL ES 或 WebGL 中開發應用程式時,需要計算投影矩陣。在舊版本的 OpenGL 中,這通常使用函式 gluPerspective、glFrustum 或 glOrtho 來完成。
在這裡,我們針對三種情況展示投影矩陣
標準透視投影(對應於 gluPerspective)
傾斜透視投影(對應於 glFrustum)
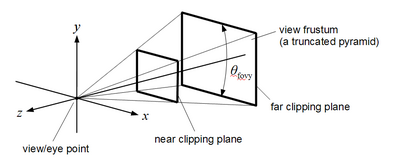
正交投影(對應於 glOrtho) 角度 θ fovy {\displaystyle \theta _{\text{fovy}}} y 方向的視場。 圖示了在 z = − n {\displaystyle z=-n} z = − f {\displaystyle z=-f} 標準透視投影 的特徵在於
一個角度 θ fovy {\displaystyle \theta _{\text{fovy}}} y {\displaystyle y}
到近裁剪平面的距離 n {\displaystyle n} f {\displaystyle f}
近裁剪平面上以中心為原點的矩形的寬高比 a {\displaystyle a} 連同視點和裁剪平面,這個以中心為原點的矩形定義了視錐體,即對於特定的投影變換可見的 3D 空間區域。所有原語和所有位於視錐體外部的原語部分都會被裁剪掉。近裁剪平面和遠裁剪平面是必需的,因為深度值以有限精度儲存;因此,不可能覆蓋無限大的視錐體。
使用引數 θ fovy {\displaystyle \theta _{\text{fovy}}} a {\displaystyle a} n {\displaystyle n} f {\displaystyle f} M projection {\displaystyle \mathrm {M} _{\text{projection}}}
M projection = [ d a 0 0 0 0 d 0 0 0 0 n + f n − f 2 n f n − f 0 0 − 1 0 ] {\displaystyle \mathrm {M} _{\text{projection}}=\left[{\begin{matrix}{\frac {d}{a}}&0&0&0\\0&d&0&0\\0&0&{\frac {n+f}{n-f}}&{\frac {2nf}{n-f}}\\0&0&-1&0\end{matrix}}\right]} with d = 1 tan ( θ fovy / 2 ) {\displaystyle {\text{ with }}d={\frac {1}{\tan(\theta _{\text{fovy}}/2)}}}
斜透視投影的引數。 斜透視投影 的特徵在於
與標準透視投影情況相同,到裁剪平面的距離為 n {\displaystyle n} f {\displaystyle f}
座標 r {\displaystyle r} l {\displaystyle l} t {\displaystyle t} b {\displaystyle b} a {\displaystyle a} θ fovy {\displaystyle \theta _{\text{fovy}}} 給定引數 n {\displaystyle n} f {\displaystyle f} r {\displaystyle r} l {\displaystyle l} t {\displaystyle t} b {\displaystyle b} M projection {\displaystyle \mathrm {M} _{\text{projection}}}
M projection = [ 2 n r − l 0 r + l r − l 0 0 2 n t − b t + b t − b 0 0 0 n + f n − f 2 n f n − f 0 0 − 1 0 ] {\displaystyle \mathrm {M} _{\text{projection}}=\left[{\begin{matrix}{\frac {2n}{r-l}}&0&{\frac {r+l}{r-l}}&0\\0&{\frac {2n}{t-b}}&{\frac {t+b}{t-b}}&0\\0&0&{\frac {n+f}{n-f}}&{\frac {2nf}{n-f}}\\0&0&-1&0\end{matrix}}\right]}
正交投影引數。 正交投影 (沒有透視縮短)如圖右側所示。引數與斜透視投影的情況相同;但是,視錐體(更準確地說,視體積)現在是一個長方體,而不是一個截斷的稜錐。
在引數 n {\displaystyle n} f {\displaystyle f} r {\displaystyle r} l {\displaystyle l} t {\displaystyle t} b {\displaystyle b} M projection {\displaystyle \mathrm {M} _{\text{projection}}}
M projection = [ 2 r − l 0 0 − r + l r − l 0 2 t − b 0 − t + b t − b 0 0 − 2 f − n − f + n f − n 0 0 0 1 ] {\displaystyle \mathrm {M} _{\text{projection}}=\left[{\begin{matrix}{\frac {2}{r-l}}&0&0&-{\frac {r+l}{r-l}}\\0&{\frac {2}{t-b}}&0&-{\frac {t+b}{t-b}}\\0&0&{\frac {-2}{f-n}}&-{\frac {f+n}{f-n}}\\0&0&0&1\end{matrix}}\right]}
視口變換的示意圖。 投影變換將視座標對映到裁剪座標,然後透過裁剪座標的第四個分量進行透視除法,對映到歸一化的裝置座標。在歸一化的裝置座標 (ndc) 中,視體積始終是一個以原點為中心的立方體,其中立方體內的座標介於 -1 和 +1 之間。然後,該立方體透過視口變換對映到螢幕座標(也稱為視窗座標),如對應圖所示。此對映的引數是視口(螢幕上呈現的矩形)左下角的座標 s x {\displaystyle s_{x}} s y {\displaystyle s_{y}} w s {\displaystyle w_{s}} h s {\displaystyle h_{s}} n s {\displaystyle n_{s}} f s {\displaystyle f_{s}}
glViewport(GLint s x {\displaystyle s_{x}} , GLint s y {\displaystyle s_{y}} , GLsizei w s {\displaystyle w_{s}} , GLsizei h s {\displaystyle h_{s}} );
glDepthRangef(GLclampf n s {\displaystyle n_{s}} , GLclampf f s {\displaystyle f_{s}} );
視口變換矩陣並不重要,因為它在固定功能階段自動應用。 然而,為了完整起見,這裡提供它。
M viewport = [ w s 2 0 0 s x + w s 2 0 h s 2 0 s y + h s 2 0 0 f s − n s 2 n s + f s 2 0 0 0 1 ] {\displaystyle \mathrm {M} _{\text{viewport}}=\left[{\begin{matrix}{\frac {w_{s}}{2}}&0&0&s_{x}+{\frac {w_{s}}{2}}\\0&{\frac {h_{s}}{2}}&0&s_{y}+{\frac {h_{s}}{2}}\\0&0&{\frac {f_{s}-n_{s}}{2}}&{\frac {n_{s}+f_{s}}{2}}\\0&0&0&1\end{matrix}}\right]}
此處描述的傳統頂點變換在“OpenGL 4.1 Compatibility Profile Specification”的第 2.12 節中進行了詳細定義,該規範可在 Khronos OpenGL 網站 上獲得。
Dave Shreiner 編寫的“OpenGL Programming Guide”一書的第 3 章(關於檢視)中給出了對頂點變換更易於理解的描述,該書由 Addison-Wesley 出版。(較舊的版本可在 網上 獲得)。
< GLSL 程式設計
除非另有說明,否則本頁上的所有示例原始碼均授予公共領域。











![{\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}=\left[{\begin{matrix}a_{1,1}&a_{1,2}&a_{1,3}&t_{1}\\a_{2,1}&a_{2,2}&a_{2,3}&t_{2}\\a_{3,1}&a_{3,2}&a_{3,3}&t_{3}\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74f8aaab560e5cb2f74f328599b57b54638f29f6)
![{\displaystyle {\text{ with }}\mathrm {A} =\left[{\begin{matrix}a_{1,1}&a_{1,2}&a_{1,3}\\a_{2,1}&a_{2,2}&a_{2,3}\\a_{3,1}&a_{3,2}&a_{3,3}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dcff6fb39a87563940e5b11f2cd33c100e98d8de)
![{\displaystyle {\text{ and }}\mathbf {t} =\left[{\begin{matrix}t_{1}\\t_{2}\\t_{3}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1762d98b5711974550f359f7b06264db7c931360)

![{\displaystyle P=\left[{\begin{matrix}p_{1}\\p_{2}\\p_{3}\\1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa4c63dd467c6eb272d3b11d2dcb27c641be56bf)

![{\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}\;P=\left[{\begin{matrix}a_{1,1}&a_{1,2}&a_{1,3}&t_{1}\\a_{2,1}&a_{2,2}&a_{2,3}&t_{2}\\a_{3,1}&a_{3,2}&a_{3,3}&t_{3}\\0&0&0&1\end{matrix}}\right]\left[{\begin{matrix}p_{1}\\p_{2}\\p_{3}\\1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13d11dfa872a62f11d49f0b7594bea2e57f36ab1)
![{\displaystyle =\left[{\begin{matrix}a_{1,1}p_{1}+a_{1,2}p_{2}+a_{1,3}p_{3}+t_{1}\\a_{2,1}p_{1}+a_{2,2}p_{2}+a_{2,3}p_{3}+t_{2}\\a_{3,1}p_{1}+a_{3,2}p_{2}+a_{3,3}p_{3}+t_{3}\\1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f96ff85224b8f3fb35ccd73c31b54bd69cca25d)
![{\displaystyle \mathrm {A} \left[{\begin{matrix}p_{1}\\p_{2}\\p_{3}\end{matrix}}\right]+\left[{\begin{matrix}t_{1}\\t_{2}\\t_{3}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff6335e75528b3f090325320d6db5f829863e54e)

![{\displaystyle \mathrm {M} _{\text{translation}}=\left[{\begin{matrix}1&0&0&t_{1}\\0&1&0&t_{2}\\0&0&1&t_{3}\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9ccb86cb24fb7ce0bf772f83efbb7391c312146)






![{\displaystyle \mathrm {M} _{\text{scaling}}=\left[{\begin{matrix}s_{x}&0&0&0\\0&s_{y}&0&0\\0&0&s_{z}&0\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b366a6c227cafdd36ec11f98948bc514b42ef014)


![{\displaystyle \mathrm {M} _{\text{rotation}}=\left[{\begin{matrix}(1-\cos \alpha )x\,x+\cos \alpha &(1-\cos \alpha )x\,y-z\sin \alpha &(1-\cos \alpha )z\,x+y\sin \alpha &0\\(1-\cos \alpha )x\,y+z\sin \alpha &(1-\cos \alpha )y\,y+\cos \alpha &(1-\cos \alpha )y\,z-x\sin \alpha &0\\(1-\cos \alpha )z\,x-y\sin \alpha &(1-\cos \alpha )y\,z+x\sin \alpha &(1-\cos \alpha )z\,z+\cos \alpha &0\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68f40eec0dda33d6ffef4c0c25b0586470d62fef)














![{\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}=\left[{\begin{matrix}x_{1}&y_{1}&z_{1}&t_{1}\\x_{2}&y_{2}&z_{2}&t_{2}\\x_{3}&y_{3}&z_{3}&t_{3}\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e00ec26b5506a084ce548aef7c370c0097ed34a)

![{\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}=\left[{\begin{matrix}\mathrm {R} &\mathbf {t} \\\mathbf {0} ^{T}&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcd0a52a1646832fca2af268dd812f7a7cbbc5ca)

![{\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}^{-1}=\mathrm {M} _{{\text{world}}\to {\text{view}}}=\left[{\begin{matrix}\mathrm {R} ^{-1}&-\mathrm {R} ^{-1}\mathbf {t} \\\mathbf {0} ^{T}&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24280cf60fc5e0c97a0623ca0dea8a080d80b017)
![{\displaystyle \mathrm {M} _{{\text{world}}\to {\text{view}}}=\left[{\begin{matrix}\mathrm {R} ^{T}&-\mathrm {R} ^{T}\mathbf {t} \\\mathbf {0} ^{T}&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c67a2e4ff6d60e39d428d0cac5ab3266f5c1b586)
![{\displaystyle {\text{with }}\mathrm {R} =\left[{\begin{matrix}x_{1}&y_{1}&z_{1}\\x_{2}&y_{2}&z_{2}\\x_{3}&y_{3}&z_{3}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba6f143978631c3e9f3414b755a11e4429c16ee3)






![{\displaystyle \mathrm {M} _{\text{projection}}=\left[{\begin{matrix}{\frac {d}{a}}&0&0&0\\0&d&0&0\\0&0&{\frac {n+f}{n-f}}&{\frac {2nf}{n-f}}\\0&0&-1&0\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43afae7ea0ce408c5a1a479a265177d988a0fb1c)





![{\displaystyle \mathrm {M} _{\text{projection}}=\left[{\begin{matrix}{\frac {2n}{r-l}}&0&{\frac {r+l}{r-l}}&0\\0&{\frac {2n}{t-b}}&{\frac {t+b}{t-b}}&0\\0&0&{\frac {n+f}{n-f}}&{\frac {2nf}{n-f}}\\0&0&-1&0\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43a44af0b15159b3378c0d628f98e88f6fa82c86)
![{\displaystyle \mathrm {M} _{\text{projection}}=\left[{\begin{matrix}{\frac {2}{r-l}}&0&0&-{\frac {r+l}{r-l}}\\0&{\frac {2}{t-b}}&0&-{\frac {t+b}{t-b}}\\0&0&{\frac {-2}{f-n}}&-{\frac {f+n}{f-n}}\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7345d54b1caa48a201493b48d21f86f2a2321ac)




![{\displaystyle \mathrm {M} _{\text{viewport}}=\left[{\begin{matrix}{\frac {w_{s}}{2}}&0&0&s_{x}+{\frac {w_{s}}{2}}\\0&{\frac {h_{s}}{2}}&0&s_{y}+{\frac {h_{s}}{2}}\\0&0&{\frac {f_{s}-n_{s}}{2}}&{\frac {n_{s}+f_{s}}{2}}\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/449547f85546e323694f1165ef4632c6991b0586)