使用 XNA/數學物理/彈道學建立遊戲

彈道學

當想到彈道學時，首先想到的可能是槍支和各種致命的子彈。但尤其是在遊戲中，彈道學可能與任何型別的彈丸的運動有關，從球到香蕉，從椰子到火箭。彈道學有助於確定這些彈丸在運動過程中的行為方式以及它們的影響。本章將展示並解釋遊戲程式設計師在程式設計任何與彈丸相關的專案時需要了解的內容。

基本物理學

任何彈丸的運動都將受到其周圍環境和它應該遵守的物理定律的很大影響。但是，重要的是要記住，遊戲不需要設定在地球上，外星星球上的體驗可能與我們所知的有效體驗完全不同。因此，此處列出的公式和解釋可能需要調整，以適應您打算讓彈丸在其間移動的任何世界。

質量和重量

質量與重量是同一個東西，這是一個常見的誤解。但物體的重量會根據其所處環境的變化而變化，而物體的質量將保持不變。重量（用 W 表示）定義為當 重力 影響質量時存在的力

$W=mg\,$ ，其中 g 是存在的重力，m 表示物體的質量

速度和加速度

速度描述了物體在一定時間內透過運動所覆蓋的距離以及這種運動的方向。它是你汽車沿著高速公路行駛或子彈在空中呼嘯而過的速度和方向。可能最常見的用來表示速度的單位是 km/h 和 m/s。h 和 s 表示一定的時間量，其中 h 代表小時，s 代表秒，km 和 m 代表公里和米，即在此時間間隔內行駛的距離。速度由一個向量定義，該向量指定運動方向，其絕對值為速度。

想象一個直直向上拋起的球，它在整個飛行過程中不會有相同的速度。它會慢下來，直到到達頂點，然後會再次加速。這被稱為加速度。它是物體速度隨時間變化的速率。牛頓第二運動定律表明，加速度取決於作用於物體上的力（例如，丟擲球的手臂和手的力）以及物體的質量（例如，球）：$F=ma\,\implies a={\frac {F}{m}}$
該物體的加速度將與施加的力方向相同。加速度的單位是距離除以時間的平方，例如 km/s²。

重力

萬有引力是作用於任何兩個物體之間的力，將它們相互吸引。這種力取決於物體的質量以及它們之間的距離。計算這種力的通用公式如下所示
$F=G{\frac {m_{1}m_{2}}{r^{2}}}$ ，其中 $m_{1}$ 和 $m_{2}$ 是物體的質量，r 是距離，G 是萬有引力常數
萬有引力常數為： $G=6.67428\times 10^{-11}\ {\mbox{m}}^{3}\ {\mbox{kg}}^{-1}\ {\mbox{s}}^{-2}=6.67428\times 10^{-11}\ {\rm {N}}\,{\rm {(m/kg)^{2}}}$

當談論地球的重力時，指的是由於存在的引力而使物體感受到的加速度。因此，重力不過是朝地球中心點的加速度。這就是為什麼從高樓掉下的物體，會一直處於自由落體狀態，直到被其他物體，例如地面，阻止。地球的重力定義如下：$g=G{\frac {m_{earth}}{r^{2}}}$，其中g是地球的重力，m是地球的質量，r是地球的半徑。
地球表面的重力約等於9.8米/秒²。

阻力

阻力會影響物體在流體和氣體中運動的速度。這種力與物體運動方向相反，因此會隨著時間的推移降低物體速度。它取決於物體的質量和形狀，以及流體的密度。由於彈道計算通常被簡化，你可能最終不需要阻力。但是，你應該考慮你的彈丸所處的流體和氣體，並調整縮放因子以獲得合適的彈道。

彈丸運動

在遊戲中，玩家所處的世界永遠不是現實世界的百分百準確的呈現。因此，在程式設計彈丸運動時，更容易簡化一些物理學，同時營造出彈丸至少在一定程度上符合人類玩家預期行為的錯覺。無論是投球還是在水下發射魚雷，彈丸在遊戲中都有兩種普遍的簡化運動模式。這些運動可以進行調整和細化，以匹配特定彈丸的預期運動。

彈丸類

建議建立一個自己的彈丸類，其中包含所有特定於彈丸的變數，例如速度，以及用於操縱和計算彈道的函式。該類的基本框架可能看起來像這樣

public class Projectile{

private Vector3 velocity;   //stores the direction and speed of the projectile
public Vector3 pos;         //current projectile position
private Vector3 prevPos;    //previous projectile position
private float totalTimePassed;         //time passed since start 
public bool bmoving = false;        //if the projectile is moving

///Constants
private const float GRAVITY = 9.8f;

    public void Start(Vector3 direction,int speed, Vector3 startPos){
        this.velocity = speed*Vector3.Normalize(direction);   
        this.pos = startPos;   //in the beginning the current position is the start position
        bmoving = true;
    }
     
    public void UpdateLinear(GameTime time){
        if(bmoving) LinearFlight(time);
    }
    
    public void UpdateArching(GameTime time){
        if(bmoving) ArchingFlight(time);
    }
}

首先，需要一些東西來觸發彈丸的運動，例如玩家的滑鼠點選。在該事件發生時，你建立一個彈丸類的新例項，並呼叫Start()以發射彈丸。你需要保留對該物件的引用，因為彈丸的位置將在每一幀進行更新，並且彈丸會被重新繪製。更新是透過呼叫UpdateLinear或UpdateArching函式完成的，具體取決於所需的彈道。新位置必須是用於在遊戲世界中繪製彈丸的變換矩陣的一部分。

在Start方法中，方向向量被歸一化，以確保在乘以速度時，結果是與初始向量方向相同且具有所需速度絕對值的向量。請記住，傳遞給Start函式的方向向量是發射彈丸的任何東西的瞄準向量。當我們假設瞄準是可變的時，它的絕對值基本上可以是任何東西。因此，這不能保證相同型別的彈丸以相同的速度移動，也不能允許玩家決定在彈丸釋放之前施加在彈丸上的力，從而改變其速度。

如果你的彈丸形狀具有明顯的正面、末端和側面，那麼需要根據其彈道改變彈丸的方向。根據尤拉旋轉定理，旋轉矩陣的向量必須是單位向量，並且是正交的。對於線性彈道，我們可以簡單地將歸一化速度向量作為方向矩陣的向前向量，並相應地構建矩陣的向右向量和向上向量。但是，由於在使用拱形彈道時，彈丸的飛行方向會不斷變化，因此更容易透過從更新前的職位中減去彈丸的當前職位，在每次更新時重新計算向前向量。為此，將以下函式放在你的彈丸類中。請記住，在繪製彈丸之前呼叫它，並將結果矩陣放入適當的變換矩陣中，遵循I.S.R.O.T順序。此順序指定了乘法變換矩陣的順序，即Identiy Matrix、Scaling、Rotation、Orientation和Translation。

public Matrix ConstructOrientationMatrix(){
    Matrix orientation = new Matrix();

    // get orthogonal vectors dependent on the projectile's aim
    Vector3 forward = pos - prevPos;     
    Vector3 right = Vector3.Cross(new Vector3(0,1,0),forward);
    Vector3 up = Vector3.Cross(right,forward);

    // normalize vectors, put them into 4x4 matrix for further transforms
    orientation.Right = Vector3.Normalize(right);
    orientation.Up = Vector3.Normalize(up);
    orientation.Forward = Vector3.Normalize(forward);
    orientation.M44 = 1;  
    return orientation; 
}

線性飛行

顯示速度為(5,3,2)的球的線性運動。

線性飛行是指沿著直線的運動。當球被直線快速丟擲時，可能會觀察到這種運動。顯然，即使這樣的球最終也會落到地面，除非在它停止之前被阻止。但是，如果例如在球離開投擲者的手後很快就被接住，那麼它的彈道看起來是線性的。為了簡化這種運動，加速度和重力被忽略，並且速度始終相同。運動方向由速度向量給出，與槍、手等的瞄準方向相同。

如果你的遊戲中存在活動彈丸，那麼XNA Update函式需要呼叫一個函式，該函式會為每個活動彈丸物件更新位置。彈丸的新位置是透過以下方式計算的
$pos=pos+velocity\times {timePassed}$，其中timePassed是自上次更新以來經過的時間。

此函式只需要一個引數，即自上次更新以來經過的遊戲時間。Cawood 和 McGee 建議透過除以 90 來縮放此時間，因為否則每幀計算的位置將相距太遠。

private void LinearFlight(GameTime timePassed){
    prevPos = pos; 
    pos = pos + velocity * ((float)timePassed.ElapsedGameTime.Milliseconds/90.0f);
}

拱形飛行

顯示球的簡化拱形彈道。

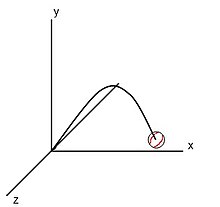
拱形彈道對於大多數飛行物體來說比線性飛行更真實，因為它考慮了重力。請記住，重力是一種加速度。為了計算具有恆定加速度的彈丸在特定時間點的位置，公式是
$pos={\frac {1}{2}}{a}{t}^{2}$，其中a是加速度，t是經過的時間。
由於重力將彈丸拉向地球，因此只有彈丸的y座標會受到影響。彈丸的上升速度會隨著時間的推移而降低，直到它停止上升並開始下降。但是，x座標和z座標不受此影響，它們與線性彈道的計算方式相同。以下公式顯示瞭如何計算y座標
${pos_{y}}=({pos_{y}}+{velocity_{y}}\times {timePassed})-{\frac {1}{2}}\times {gravity}\times {totalTimePassed}^{2}$
，其中totalTimePassed是自彈丸開始運動以來經過的時間。
被減數等於線性飛行公式，減數是由於重力導致的向下加速度。很明顯，彈丸速度越低，速度方向越指向地面，重力就會越快獲勝。此函式將更新彈丸的彈道。

private void ArchingFlight(GameTime timePassed){
    prevPos = pos; 
    // accumulate overall time
    totalTimePassed += (float)timePassed.ElapsedGameTime.Milliseconds/4096.0f ;
    
    // flight path where y-coordinate is additionally effected by gravity
    pos = pos + velocity * ((float)timePassed.ElapsedGameTime.Milliseconds/90.0f);
    pos.Y = pos.Y - 0.5f * GRAVITY * totalTimePassed * totalTimePassed;
}

我將新增到總時間的時間縮小了，這樣重力就不會立即生效。對於速度為 1，按 4096 縮放會產生一個不錯的飛行路徑。另外，編譯器希望能夠進行合理的處理並最佳化除以 4096，因為它是 2 的倍數。你可能想嘗試調整縮放因子。如果你的遊戲不是在地球上設定的，你還應該考慮重力常數是否不同。

影響

一旦你的彈丸開始移動，你可能想進行一些碰撞檢測，如果你希望它擊中任何東西。有關如何進行碰撞檢測的更多資訊和詳細資訊，請檢視關於碰撞檢測的章節。如果檢測到碰撞，就該考慮彈丸和被擊中物體將會發生什麼。撞擊的效果高度依賴於你的彈丸是什麼。球可以彈回，非常快的小子彈可能會穿透物體並繼續移動，而另一方面，一個大的魚雷可能會爆炸。在被擊中物體的類中決定適當的反應更容易，並且可能播放指定的音效或動畫。否則，你必須在彈丸類中跟蹤彈丸對遊戲中每個物體可能產生的所有效果。為了保持簡單，只需在彈丸類中包含一些定義彈丸可能行為的函式，並在檢測到碰撞時從被擊中物體類中呼叫適當的函式。例如，當球擊中地面時，它可能會簡單地彈回。為了模擬這種行為，在彈丸類中使用以下函式，並在檢測到球到達地面時呼叫它。它所做的只是反射入射方向並降低速度。當速度為零或更小時，球已停止移動，無需繼續更新其飛行路徑。'reflectionAxis' 向量僅包含 1，除了需要反轉方向的軸，此值必須為 -1。

public void bounce(Vector3 incomingDirection, Vector3 reflectionAxis){
    //reflect the incoming projectile and normalize it so it's "just" a direction
    Vector3 direction = Vector3.Normalize(reflectionAxis* incomingDirection);
    speed -= 0.5f;                   // reduces the speed so the arche becomes lower
    velocity = speed * direction;    // the new velocity vector
    totalTimePassed= 0;                     // gravity starts all over again
    if (speed <= 0)bmoving= false;   // no speed no movement
}

當球應該從地面反彈回來時，對該函式的呼叫可能類似於以下程式碼，因此它的 y 方向需要反轉。

ball.bounce(ball.position - ball.previousPosition, new Vector3(1, -1, 1));