普通力學/扭矩和角動量

普通力學

扭矩

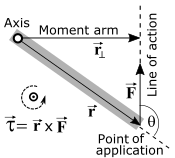
扭矩是作用於一個質量上的力，使它繞一個點（稱為原點）旋轉。它被定義為

{\vec {\tau }}={\vec {r}}\times {\vec {F}}

其中 $r$ 是質量相對於原點的位移。

需要注意的是，在許多情況下扭矩為 0。如果力的方向直接指向或遠離原點，叉積為零，導致扭矩為零，即使力不為零。同樣地，如果 $r=0$ ，扭矩為 0。因此，作用於原點的力不會產生扭矩。這兩個極限直觀上是有道理的，因為它們都沒有使質量繞原點旋轉。

質量相對於點 O 的角動量定義為

{\vec {L}}={\vec {r}}\times {\vec {p}}

其中 p 是質量的普通（也稱為“線性”）動量。如果物體的運動直接指向或遠離原點，或者它位於原點，則角動量為 0。

如果我們取位置向量和牛頓第二定律的叉積，我們會得到一個將扭矩和角動量聯絡起來的方程

{\vec {r}}\times {\vec {F}}={\vec {r}}\times {\frac {d{\vec {p}}}{dt}}={\frac {d}{dt}}({\vec {r}}\times {\vec {p}})-{\frac {d{\vec {r}}}{dt}}\times {\vec {p}}

由於平行向量的叉積為零，這簡化為

{\vec {\tau }}={\frac {d{\vec {L}}}{dt}}

這是牛頓第二定律的旋轉版本。

對於扭矩和角動量，原點的位置是任意的，通常選擇最方便的位置。但是，必須為扭矩和角動量選擇相同的原點。

對於中心力的情況，即沿著兩個物體之間的中心線作用的力（如重力），通常存在一個特別方便的原點選擇。如果原點放在太陽的中心（假設它不會受到行星引力的影響而移動），那麼太陽的引力對行星施加的扭矩為 0，這意味著行星繞太陽中心的角動量是恆定的。其他任何原點選擇都不會產生這種方便的結果。

我們已經瞭解了兩個基本的守恆定律——能量和線性動量的守恆定律。我們相信角動量在孤立系統中也是守恆的。換句話說，粒子可以在彼此之間交換角動量，但是孤立於外部影響的所有粒子的角動量的向量和必須保持恆定。

在現代觀點中，角動量守恆是空間各向同性性的結果——即空間的特性不依賴於方向。這與普通動量守恆是空間齊次性的結果完全類似。我們記得，普通動量守恆是空間齊次性的結果。

如果一個物體繞著一個軸旋轉， $n$ 是單位向量，以頻率 $\omega$ 旋轉，我們說它具有角速度 ${\vec {\omega }}$ 。儘管名稱如此，但這 *並非* 角度變化率，甚至不是向量變化率。

如果一個常數向量 ${\vec {r}}$ 以角速度 ${\vec {\omega }}$ 繞固定點旋轉，則

{\frac {d{\vec {r}}}{dt}}={\vec {\omega }}\times {\vec {r}}

這意味著加速度始終垂直於速度和旋轉軸。

當軸發生變化時， ${\vec {\omega }}$ 可以定義為使得此關係成立的向量。

注意，在這個等式左側， ${\vec {r}}$ 是固定座標系中的向量，具有可變分量，而在等式右側，其分量是在運動座標系中給出的，在那裡它們是固定的。

我們可以使用下標來更清楚地區分它們， $r$ 表示旋轉的， $f$ 表示固定的，然後將此擴充套件到任意向量

{\frac {d{\vec {g}}_{f}}{dt}}={\frac {d{\vec {g}}_{r}}{dt}}+{\vec {\omega }}\times {\vec {g}}_{f}

對於 *任何* 向量 ${\vec {g}}$

利用這個，我們可以寫出旋轉系中的牛頓第二定律。

{\begin{aligned}{\vec {F}}_{f}&=m{\dfrac {d{\vec {v}}_{f}}{dt}}\\&=m{\dfrac {d{\vec {v}}_{r}}{dt}}+m{\vec {\omega }}\times {\vec {v}}_{f}\\&=m{\ddot {\mathbf {r} }}_{r}+m{\boldsymbol {\omega }}\times \left(2{\dfrac {d_{2}{\vec {r}}_{r}}{dt_{2}}}+{\vec {\omega }}\times {\vec {r}}_{f}\right)\end{aligned}}

或者，重新排列

m{\vec {a}}_{r}={\vec {F}}-2m({\vec {\omega }}\times {\vec {v}}_{r})-m{\vec {\omega }}\times ({\vec {\omega }}\times {\vec {r}})

質量的行為就好像有兩個額外的力作用於它。第一項， ${\vec {\omega }}\times {\vec {v}}$ 被稱為*科里奧利*力。第二項是熟悉的離心力。