直角座標系,也稱為笛卡爾座標系,是一種系統化的定位物體的方法。它是由一位名為笛卡爾的數學家發明的。它與地理或計算機素養中的座標系相似,但並不完全相同。
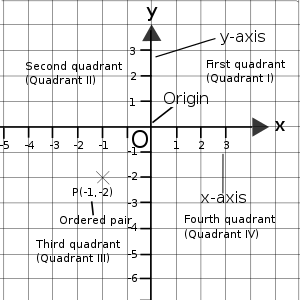
笛卡爾平面相關基本術語的總結 直角座標平面,或稱為笛卡爾平面,由兩條軸組成,即x軸和y軸。x軸是水平軸,而y軸是垂直軸。這兩條軸的交點稱為原點,始終命名為O 。x軸和y軸上是刻度,這與統計圖表中的刻度非常相似,只是這裡有負數。事實上,它們看起來像數軸,一條水平,一條垂直,‘0’點重疊。
我們可以使用有序對在座標系中定位一個點。有序對由兩個數字組成:兩條軸的讀數。我們先寫x軸的讀數,然後寫y軸的讀數,像這樣:(x, y)。座標平面被分成四個部分:第一象限(象限I)、第二象限(象限II)、第三象限(象限III)和第四象限(象限IV)。四個象限的位置可以在右邊的圖中找到。一個點可以位於這四個象限中的任何一個,也可以位於x軸、y軸或原點。我們可以僅透過檢視點的座標來找出有序對的一些基本屬性。
象限I: (x , y )
象限II: (-x , y )
象限III: (-x , -y )
象限IV: (x , -y )
x軸: (x 或 -x , 0)
y軸: (0, y 或 -y )
原點: (0, 0) 確定一個點的有序對時,請記住刻度不一定是一對一的。這意味著數字不必是0, 1, 2, 3, 4。它們也可以是0, 2, 4, 6, 8,甚至5, 10, 15, 20。
如果您完全確定兩點形成一條水平線或垂直線,水平線的定義是平行於x軸,垂直線的定義是平行於y軸,那麼您可以參考另一個點,而無需刻度的幫助來找到一個或兩個點的座標。例如,如果P (3, 4) 與Q (3, y ) 位於同一條垂直線上,那麼y = 4。
我們將用一個複雜的問題來介紹下一部分(見右邊的圖)。
求
QP 的長度所有陰影區域的面積之和
如果F :(-2, -3),那麼I 的座標 乍一看有點複雜,所以讓我們從第一象限上的直線QP 開始,這條直線看起來相當容易。如果可以的話,我們將計算出所有未知數,並解決第一個目標。首先,讓我們看看P 的座標。它們是(1, 2)。由於P 和Q 位於同一條水平線上,所以它們的y 座標必須相同。因此,Q 的座標必須是(3, 2)。換句話說,z = 2。要找到PQ的長度,我們只需找到它們的x 座標之差即可;在本例中,3 - 1 = 2 個單位。因此,QP = 2 個單位。在數學表達中,應該是
∵ The y -coordinate of P = 2 ∴ z = 2 {\displaystyle {\begin{aligned}\because {\text{The }}y{\text{-coordinate of }}P=2\\\therefore z=2\end{aligned}}}
The length of P Q = 3 − 1 = 2 units {\displaystyle {\begin{aligned}{\text{The length of }}\ PQ&=3-1\\&=2{\text{ units}}\end{aligned}}}
太好了!現在我們已經解決了第一個目標,讓我們繼續研究第二象限上的小三角形。同樣,我們將計算出所有未知數。首先,讓我們看看C 的x 座標。我們已經知道z = 2,所以-z 必須是 -2,C 的x 座標也是如此。y 座標呢?我們知道B和C位於同一條水平線上,所以它們的y 座標必須相同。因此,C 的y 座標也必須是1,並且y = 1。B 的x 座標,稱為x ,也是缺失的。由於A和B位於同一條垂直線上,所以它們的x 座標必須相同。因此,我們可以推斷x = -4。在數學表示式中
The x -coordinate of C = − z = 1 {\displaystyle {\begin{aligned}{\text{The }}\ x{\text{-coordinate of }}\ C&=-z\\&=1\end{aligned}}}
∵ The y -coordinate of B = 1 ∴ y = 1 {\displaystyle {\begin{aligned}\because {\text{The }}y{\text{-coordinate of }}B=1\\\therefore y=1\end{aligned}}}
∵ The x -coordinate of A = − 4 ∴ x = − 4 {\displaystyle {\begin{aligned}\because {\text{The }}x{\text{-coordinate of }}A=-4\\\therefore x=-4\end{aligned}}}
接下來,我們將求出三角形 ABC 的面積。這在求陰影區域的總面積時將非常有用。在計算之前,我們必須先求出三角形的底和高。你還記得三角形面積公式嗎?它是底乘以高除以二。讓我們選擇 BC 作為三角形的底。由於 AB 和 BC 互相垂直,AB 可以作為高。由於 BC 是水平線,BC 的長度就是 B 和 C 的 x 座標之差。即 -4 和 -1,所以 BC 的長度為 [(-1)-(-4)] 單位 = 3 單位。對於 AB,情況則相反。由於 AB 是垂直線,我們應該找到它們的 y 座標之差。在本例中,即為 (3-1) 單位 = 2 單位。因此,三角形 ABC 的面積為 (3-2) 平方單位 = 1 平方單位。讓我們用數學表示式來表示。
The length of B C = x − ( − z ) units = [ ( − 1 ) − ( − 4 ) ] units = 3 units {\displaystyle {\begin{aligned}{\text{The length of }}\ BC&=x-(-z){\text{ units}}\\&=[(-1)-(-4)]{\text{ units}}\\&=3{\text{ units}}\end{aligned}}}
The length of A B = 3 − 1 units = 2 units {\displaystyle {\begin{aligned}{\text{The length of }}\ AB&=3-1{\text{ units}}\\&=2{\text{ units}}\end{aligned}}}
The area of △ A B C = B C × A B 2 sq. units = 3 × 2 2 sq. units = 3 units {\displaystyle {\begin{aligned}{\text{The area of }}\ \triangle ABC&={\frac {BC\times AB}{2}}{\text{ sq. units}}\\&={\frac {3\times 2}{2}}{\text{ sq. units}}\\&=3{\text{ units}}\end{aligned}}}
現在我們只需要計算出兩個下象限圖形的面積。該圖形的形狀類似於梯形,旁邊粘著一個三角形,中間有一個洞。利用我們之前學到的知識,你應該可以算出 a = -4 且 b = -6。注意,我們已經知道上面 -z 的值,即 -2。現在我們要找到梯形、三角形和正方形孔的面積。讓我們先計算三角形的面積。從 Z 點畫一條與 XY 垂直的虛線,並命名為 R。參考 X 和 Z 點,R 點的座標為 (-4, -5)。ZR 和 XY 的長度應分別為 1 和 4,因此三角形 XYZ 的面積一定是 2 平方單位。具體細節如下面的數學表示式所示。
∵ The x -coordinate of X = − 4 ∴ a = − 4 {\displaystyle {\begin{aligned}\because {\text{The }}x{\text{-coordinate of }}X=-4\\\therefore a=-4\end{aligned}}}
∵ The y -coordinate of Y = − 6 ∴ b = − 6 {\displaystyle {\begin{aligned}\because {\text{The }}y{\text{-coordinate of }}Y=-6\\\therefore b=-6\end{aligned}}}
The y -coordinate of D = − z = − 2 {\displaystyle {\begin{aligned}{\text{The }}y{\text{-coordinate of }}D=-z\\=-2\end{aligned}}}
The length of Z R = ( − 5 ) − ( − 4 ) units = 1 units {\displaystyle {\begin{aligned}{\text{The length of }}\ ZR&=(-5)-(-4){\text{ units}}\\&=1{\text{ units}}\end{aligned}}}
線段 X Y = ( − 2 ) − ( − 6 ) 個單位 = 4 個單位 {\displaystyle {\begin{aligned}{\text{The length of }}\ XY&=(-2)-(-6){\text{ units}}\\&=4{\text{ units}}\end{aligned}}}
三角形 △ X Y Z = Z R × X Y 2 平方單位 = 1 × 4 2 平方單位 = 2 平方單位 {\displaystyle {\begin{aligned}{\text{The area of }}\ \triangle XYZ&={\frac {ZR\times XY}{2}}{\text{ sq. units}}\\&={\frac {1\times 4}{2}}{\text{ sq. units}}\\&=2{\text{ sq. units}}\end{aligned}}}
現在我們要找到直角梯形的面積。你還記得梯形的面積公式嗎?它是平行邊之和乘以高除以二。我們需要找到平行邊的長度和高度才能求出面積。我們已經知道高度 *XY*。線段 *XD* 和 *YE* 的長度分別為 9 和 8,所以梯形的面積為 34 平方單位。具體細節如下。
線段 X D = ( − 4 ) − 5 個單位 = 9 個單位 {\displaystyle {\begin{aligned}{\text{The length of }}\ XD&=(-4)-5{\text{ units}}\\&=9{\text{ units}}\end{aligned}}}
線段 Y E = ( − 4 ) − 4 個單位 = 4 個單位 {\displaystyle {\begin{aligned}{\text{The length of }}\ YE&=(-4)-4{\text{ units}}\\&=4{\text{ units}}\end{aligned}}}
梯形 X Y D E = ( X D + Y E ) × X Y 2 平方單位 = ( 9 + 4 ) × 4 2 平方單位 = 26 平方單位 {\displaystyle {\begin{aligned}{\text{The area of trapezium}}\ XYDE&={\frac {(XD+YE)\times XY}{2}}{\text{ sq. units}}\\&={\frac {(9+4)\times 4}{2}}{\text{ sq. units}}\\&=26{\text{ sq. units}}\end{aligned}}}
我們的下一步是找到正方形的面積。正方形的面積公式是邊長的平方,所以正方形 *FGHI* 的面積是 *z*2 = 22 單位 = 4 單位。
正方形 F G H I = F I 2 平方單位 = z 2 平方單位 = 2 2 平方單位 = 4 平方單位 {\displaystyle {\begin{aligned}{\text{The area of square}}\ FGHI&=FI^{2}{\text{ sq. units}}\\&=z^{2}{\text{ sq. units}}\\&=2^{2}{\text{ sq. units}}\\&=4{\text{ sq. units}}\end{aligned}}}
第二點的最後部分是使用我們從前面章節中學到的平面圖形等技能,計算出陰影區域的總面積。第三和第四象限的陰影區域 = 五邊形 XZYED 的面積 - 正方形 FGHI 的面積 = 三角形 XYZ 的面積 + 梯形 XYDE 的面積 - 正方形 FGHI 的面積 = (2+26-4) 平方單位 = 24 平方單位。然後我們將它加到三角形 ABC 的面積,得到 (24+3) 平方單位 = 27 平方單位。數學表示式如下所示。
The shaded area in quadrants III and IV = Area of △ X Y Z sq. units + Area of trapezium X Z Y E D − Area of square F G H I = ( 2 + 26 − 4 ) sq. units = 24 sq. units {\displaystyle {\begin{aligned}&{\text{The shaded area in quadrants III and IV }}\\&={\text{Area of }}\triangle XYZ{\text{ sq. units}}+{\text{Area of trapezium }}XZYED-{\text{Area of square }}FGHI\\&=(2+26-4){\text{ sq. units}}\\&=24{\text{ sq. units}}\end{aligned}}}
The sum of all shaded areas = ( 24 + 3 ) sq. units = 27 sq. units {\displaystyle {\begin{aligned}{\text{The sum of all shaded areas }}&=(24+3){\text{ sq. units}}\\&=27{\text{ sq. units}}\end{aligned}}}
既然我們已經完成了兩個目標,現在該尋找第三個目標了。第三個目標需要一種與前面我們使用的方法相反的技術。你可能已經注意到,第三個目標與其他目標不同,它要求找到座標,而不是測量值。請記住,我們從問題中知道的唯一座標是點 *F* 的座標。還要記住,正方形的四條邊都相等。既然我們可以根據線段端點的座標找到線段的長度,那麼我們也可以根據線段的長度找到端點的座標。
那麼,我們究竟是如何做到的呢?*F* 的座標是 (-2, -3)。我們可以找到 *I* 的 *y* 座標,我們已經知道它與 *F* 的 *y* 座標相同。因此,*y* 座標為 -3。但是 *x* 座標呢?既然我們知道 *FI* = *z* = 2 個單位,我們可以算出 *I* 的 *x* 座標為 [(-2)+2)] 個單位 = 4 個單位。請記住,我們正在尋找的端點的座標相對於我們已經知道的端點的座標的位置是重要的。如果 *I* 在 *F* 的右邊,而不是左邊,它的 *x* 座標將為 [(-2)-2)] 個單位 = -4 個單位。如果 *I* 在 *F* 的上方或下方,它們的 *x* 座標將相同,而 *I* 的 *y* 座標將為 [(-3)-2)] 個單位 = -5 個單位(下方)或 [(-3)+2)] 個單位 = -1 個單位(上方)。
∵ The y -coordinate of F = − 3 ∴ The y -coordinate of I = − 3 {\displaystyle {\begin{aligned}\because {\text{The }}y{\text{-coordinate of }}F=-3\\\therefore {\text{The }}y{\text{-coordinate of }}I=-3\end{aligned}}}
∵ F I = z = 2 units {\displaystyle {\begin{aligned}\because FI=z\\=2{\text{ units}}\end{aligned}}} ∴ The x -coordinate of I = [ ( − 2 ) + 2 ) ] = 4 {\displaystyle {\begin{aligned}\therefore {\text{The }}x{\text{-coordinate of }}I=[(-2)+2)]\\&=4\end{aligned}}}
就是這樣!我們不僅學習瞭如何在直角座標系中計算圖形的長度和麵積以及點的座標,而且還看到了一個重要的例子,說明了面積是如何計算的。







![{\displaystyle {\begin{aligned}{\text{The length of }}\ BC&=x-(-z){\text{ units}}\\&=[(-1)-(-4)]{\text{ units}}\\&=3{\text{ units}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ed707e08315fbae43e73fe3df868022c03d38b7)
















![{\displaystyle {\begin{aligned}\therefore {\text{The }}x{\text{-coordinate of }}I=[(-2)+2)]\\&=4\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a56cf9a7a5b74462fa93f938d0c4c785f52b777f)