歷史地質學/放射性衰變
作為對放射性年代測定文章的序言,讀者應該瞭解放射性衰變機制。本文提供了對它是什麼以及它是如何工作的非技術性解釋。
讀者應該從高中回憶起原子的原子核由質子(帶正電荷的粒子)和中子(不帶電荷的粒子,其質量幾乎與質子相同)組成。原子核被電子雲包圍,電子是帶負電荷的粒子,其重量可以忽略不計。電子的數量等於質子的數量。
原子中質子的數量是它的原子序數,質子和中子的總和給出它的原子量。
原子的化學性質由其電子的行為決定,因此實際上由其原子序數決定。因此在化學中,原子根據其原子序數被分類為元素:例如,像碳這樣的元素被定義為具有 6 的原子序數。然而,兩個原子可以具有相同的原子序數但不同的原子量。因此,例如,12C(碳-12)具有 6 個質子和 6 箇中子,而14C(碳-14)具有 6 個質子和 8 箇中子。它們都是碳,它們在化學上都表現得像是碳,但它們具有不同的原子量。因此,它們被稱為是同一元素,即碳,但它們是碳的不同同位素。同位素由其原子序數和原子量定義。
在上一段的示例中,我們展示了用於同位素的符號。具有 6 個質子和 8 箇中子的原子寫為14C。它具有 6 個質子的事實是由“C”揭示的,這是碳的化學符號;根據定義,所有碳原子都具有 6 個質子。它具有 8 箇中子的事實是由寫在“C”左側上方的“14”揭示的:這是同位素的原子量,因此由於原子量是質子和中子的數量,並且由於所有碳原子都具有 6 個質子,這告訴我們碳的這種同位素必須具有 8 箇中子。
放射性衰變可以定義為任何自發事件,這些事件會改變原子核的狀態,在此過程中從原子核中釋放能量。除了伽馬衰變(這裡我們無需關心),這將涉及改變質子或中子的數量,或兩者都改變,因此也會改變原子序數、原子量或兩者都改變。
衰變可能發生的機制有很多。對於我們的目的,最重要的機制是

- α 衰變。在這種衰變形式中,原子核會發射一個由兩個中子和兩個質子組成的α 粒子,使原子序數減少兩個,原子量減少四個。
- β 負衰變。在這種衰變形式中,原子中的一箇中子透過原子發射一個電子而被轉化為一個質子。因此,原子序數增加一個,而原子量保持不變。
- β 正衰變。在這種衰變形式中,一個質子透過發射一個正電子(一種類似於電子但帶正電荷的粒子)而被轉化為一箇中子,結果是原子序數減少一個,而原子量保持不變。
- 電子俘獲。在這種衰變形式中,原子自身的一個電子與它自己的一個質子結合,將質子轉化為一箇中子。這使原子序數減少一個,同時使原子量保持不變。
當衰變發生時,原始原子被稱為母原子,而衰變產生的新原子被稱為子原子。那些由放射性衰變產生的同位素被稱為放射成因。並非所有同位素都會發生衰變:那些會發生衰變的被稱為不穩定同位素(或放射性同位素),反之,那些不會發生衰變的被稱為穩定同位素。因此,例如,12C 是穩定的,並將永遠保持12C;相反,14C 不穩定,並傾向於衰變為14N(氮-14)。正如我們從這個例子中看到的,同一元素的不同同位素在穩定性上有所不同是完全可能的。
讀者應該注意,當母原子衰變為子原子時,子原子不一定穩定;有時子原子將進一步發生衰變。這種情況被稱為衰變鏈。
理解放射性衰變如何以及為什麼發生很重要。根據物理學家的說法,放射性衰變是隨機發生的:一個(例如)22Na(鈉-22)原子會發生β 衰變併產生一個22Ne(氖-22)原子,僅僅是因為它的號碼出來了。
原子的年齡與之無關。以類比為例,一個人用六發左輪玩俄羅斯輪盤賭。他每次玩都有 1/6 的機率死亡,無論他玩了多長時間都是如此。放射性衰變也是如此。如果我們有一個22Na 原子,那麼無論它有多老,它在接下來的 2.6 年內都有 50% 的機率衰變;如果它在 2.6 年內倖存下來,那麼它在接下來的 2.6 年內有 50% 的機率衰變;等等。
考慮一下如果我們有一個大的22Na 樣本這意味著什麼。因為樣本很大,它的行為將非常接近我們對其統計期望值:因此,在 2.6 年後,50% 的原子將衰變為22Ne;在接下來的 2.6 年後,剩餘的22Na 的 50% 將衰變(只剩下原始22Na 的 25%);在接下來的 2.6 年後,這些22Na 原子的 50% 將衰變,剩下原始樣本的 12.5%;等等。
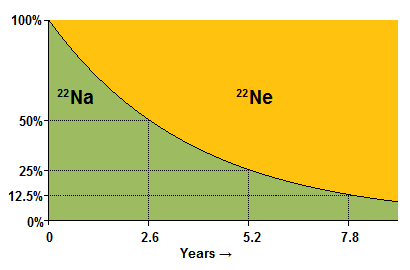
這個 2.6 年的數字被稱為22Na 的半衰期:也就是說,一個22Na 原子有 50% 的機率衰變的時間;或者,等效地,我們統計期望值是樣本的 50% 衰變的時間。
這種情況在數學上是眾所周知的,可以用指數衰減方程表示
- N(t) = N0 × 2-t/2.6
其中,N0 是22Na 的原始數量,2.6 是以年為單位的半衰期,t 是以年為單位測量的經過時間,N(t) 是時間t 時樣本中剩餘的22Na 的數量。
這種情況可以用右邊的圖表來表示。
為了便於解釋,我們始終使用22Na 作為示例,但相同的規則適用於所有放射性同位素,唯一的區別是不同同位素的半衰期不同:例如107Pd(鈀-107)的半衰期為 650 萬年。
人們有時會對這樣的陳述感到驚訝:他們問道,當我們沒有觀察107Pd 樣本 650 萬年來驗證它需要多長時間才能讓它的一半衰變時,我們怎麼能說呢?
然而,這並不是一個真正的問題。畢竟,以類比為例,警察無需觀察你的汽車一個小時才能報告你正以 72 公里/小時的速度行駛。觀察你在一秒鐘內行駛 20 米就足夠了,然後進行計算。
同樣,如果我們只花一年觀察一個107Pd 樣本,並發現在這段時間內,該樣本只有 0.0000106638% 衰變,那麼我們可以寫
- 100 - 0.0000106638 = 100 × 2-1/h
然後解方程求解h 將得到以年為單位的半衰期。
從這個例子中可以明顯看出,我們對半衰期的瞭解的準確性將取決於我們對樣本初始大小和其衰變速率的測量準確性。
因此,每個不穩定的同位素都有其自己的特徵半衰期。更重要的是,對於每個同位素來說,這個半衰期是恆定的:它是同位素的一個屬性,幾乎不受外部環境的影響。
我們如何知道這一點?首先,從原理上講應該是正確的:它可以從量子力學的基本定律推匯出來。其次,它得到了實際觀測的證實:在發現放射性衰變後不久,科學家就開始嘗試透過將不穩定同位素置於熱、壓力、磁場等環境下改變其衰變速率,但結果是負面的。
在某些同位素中,根據它們與其他化學物質形成的分子鍵的不同,觀察到了微小的變化。例如,7Be(鈹-7)的衰變速率會根據其所處化學環境的不同而變化約 1%。從理論上講,7Be 應該特別容易受到這種影響:它是一個非常小的原子,並且透過電子俘獲衰變。即便如此,這種變化也很小。出於同樣的原因,在對 7Be施加強壓後,也實現了更小的變化。
我們還應該提到奇特的同位素 187Re(錸-187)。由於原子核衰變時釋放的能量非常小,因此可以透過電離改變其半衰期。如果它完全剝奪了所有電子,它的半衰期將從 430 億年下降到 33 年!然而,由於這種情況在地球上除物理實驗室外不會發生,因此在所有地質目的中,我們可以將它的半衰期視為 430 億年。
因此,為了真正影響同位素的半衰期,需要採用高度人工的方法——例如將它丟入核反應堆的核心。在自然界,尤其是在岩石中,有充分的理論和觀測理由得出結論,不穩定同位素將具有恆定或幾乎恆定的半衰期,因此將以規律和可預測的方式發生衰變,並且已經發生了衰變。
敏銳的讀者可能已經猜到了事情的發展方向。在不穩定同位素的衰變中,我們有一組自然過程,每個過程都以完全可預測的速率進行。
簡單地說,放射性年代測定的理念是這樣的。如果我們有一塊岩石,並且知道岩石剛形成時所含的某種放射性同位素的原始數量,並且知道它的半衰期,並且能夠準確測量目前岩石中該同位素的數量,那麼我們就可以計算出岩石的年齡。或者,如果我們知道放射性同位素的子同位素的原始數量和目前數量,那麼我們同樣可以計算出岩石的年齡。這種絕對年代測定技術被稱為 **放射性年代測定**。
但是,我們如何才能知道岩石的原始成分呢?這個問題的答案取決於我們談論的是哪種放射性同位素;因此,現在是停止籠統地談論,而是詳細瞭解放射性年代測定的具體方法的時候了。這些將是接下來的幾篇文章的主題。
