IB 物理/熱物理
熱能從高溫物體傳遞到低溫物體。
T(K) = t/(°C) +273
將攝氏溫度轉換為開氏溫度,需要加上 273.15。將開氏溫度轉換為攝氏溫度,需要減去 273.15。
| 概念 | 解釋 |
|---|---|
| 溫度 | 是物質中分子平均動能的量度。 |
| 內能 | 是物質中平均動能和勢能的量度。 |
| 熱能 | 是系統與其周圍環境之間非機械的能量傳遞。 |
| 詞語 | 定義 |
|---|---|
| 摩爾 | 含有與 12g 碳-12 中原子數目相同的粒子的物質的量。 |
| 摩爾質量 | 一摩爾物質的質量。 |
| 阿伏伽德羅常數 | 是每摩爾粒子數。該數值可以在 IB 物理資料手冊中找到,等於 6.023 × 1023。 |
| 詞語 | 定義 |
|---|---|
| 比熱容(SHC) | 1kg 物質升高 1K 溫度所需的熱能。 |
| 熱容 | 物質升高 1K 溫度所需的熱能。 |
| 相態 | 解釋 |
|---|---|
| 固態 | 宏觀上,體積和形狀固定。分子圍繞平均位置振動。 |
| 液態 | 體積固定,但形狀可變。分子振動,但不固定在某個位置。分子可以自由移動。 |
| 氣態 | 分子會膨脹以充滿容器。分子不處於固定位置。 |
| 相變 | 解釋 |
|---|---|
| 凝固 | 運動較慢的液體分子開始失去能量,並固定在某個位置。液體轉變為固體。 |
| 熔化 | 固定的固體分子獲得能量,並開始運動得更多。固體轉變為液體。 |
| 蒸發 | 液體表面運動較快的分子逃逸,使液體冷卻。液體轉變為氣體。 |
| 沸騰 | 液體內部運動較快的分子逃逸。液體轉變為氣體。 |
| 冷凝 | 運動較慢的氣體分子失去能量。氣體轉變為液體。 |
相變與分子勢能的增加或減少有關,而不是動能。因此,在相變過程中溫度不變。
蒸發發生在液體的表面,而沸騰發生在整個液體中。
比潛熱是相變過程中每單位質量吸收或釋放的能量。
其中,
L= 比潛熱,單位 Jkg^-1
Q= 能量,單位 J
m= 質量,單位 kg
壓力是作用在單位面積上的力。它以帕斯卡為單位。
假設
- 牛頓定律適用於分子行為
- 不存在分子間力
- 分子是點
- 碰撞是彈性的
- 這些碰撞不花費時間
溫度是理想氣體分子平均隨機動能的量度
| 定律 | 對理想氣體的影響 |
|---|---|
| 壓強定律 | 氣體的壓強與其溫度成正比 |
| 查理定律 | 氣體的體積與其溫度成正比 |
| 玻意耳定律 | 氣體的壓強與其體積成反比 |
麥克斯韋-玻爾茲曼分佈曲線
氣體的速度(或能量)分佈曲線通常以速度為橫軸,分子數量為縱軸。曲線從原點開始,上升到峰值,然後呈指數下降,就像橫軸是一條漸近線一樣。較高的溫度曲線更“平坦”,峰值更低,但在峰值之後下降速度更慢。
蒸發是單個分子從液體中逃逸的過程。這發生在任何液體中,除非液體處於封閉系統中,否則最終所有液體都會蒸發。
隨著液體蒸發,其溫度會降低。冷卻效應是由於快速移動的分子逃逸,留下緩慢移動的分子。這意味著分子的平均速度降低,因此液體的溫度降低。這是蒸發冷卻的原理。
線性膨脹係數用符號 a 表示,定義了物體(例如一根金屬絲)的長度在給定的溫度變化下變化多少。它用於公式 ΔL = a x L0 x ΔT,其中 L0 是初始長度,ΔL 是變化量。
重要的是要理解,L0 應該出現在這個公式中。膨脹是由於分子移動得更快,因此在振動時距離更遠。因此,分子越多,在給定變化情況下膨脹越大,因為所有分子之間的空間都會膨脹。
固體的熱膨脹是由於組成粒子的振動幅度增加。隨著溫度升高(即熱量增加),粒子獲得更多能量,這些能量變成 Ek(儘管不是平移能量),導致振動幅度更大。因此,分子之間有更大的空間,因此整個固體變得更大。
線性膨脹方程可以應用於任何方向(在大多數物質中),因此可以用來計算面積和體積的膨脹。要計算面積,只需計算兩個垂直方向的膨脹,然後計算這兩個變化導致的面積變化。對於體積,計算三個垂直方向的膨脹,然後計算體積變化。
利用熱膨脹
- 雙金屬片(其中兩條不同的金屬片,具有不同的 a 值,在中間粘合在一起),當加熱或冷卻時會彎曲(因為其中一側的金屬膨脹/收縮速度快於另一側)。這可以用來閉合或斷開電路,通常用於恆溫器(即當溫度低於或高於某個溫度時會開啟或關閉加熱器的裝置)。
- 當金屬環膨脹時,外邊緣和中間的孔都會膨脹(這可能並不明顯,但這是真的)。因此,可以擴大“孔”使環可以套在某個物體上,然後當它冷卻時會鎖緊。這種技術用於將帶子安裝在馬車輪上(如今這種情況很少見)。
- 液體的體積膨脹是水銀溫度計和酒精溫度計的基礎。隨著溫度升高,水銀的體積增加,將其推向管子上方。
克服熱膨脹問題
- 橋樑由混凝土塊建造,如果溫度升高,它們會相互膨脹並破碎。為了克服這個問題,在塊之間留有間隙,以便它們膨脹。這就是橋樑上存在間隙的原因,也是您開車經過橋樑時聽到“砰砰”聲的原因。鐵路軌道也是如此。
- 蒸汽管道必須允許膨脹,因為它們在溫度上有很大變化(即,管道里有蒸汽時和沒有蒸汽時)。為了允許這種情況,管道連線到“角落”接頭。這些接頭類似於 L 形,因此垂直管道可以在接頭中上下膨脹,而水平管道可以在左右膨脹,而不會扭曲管道的形狀(它還會建立一系列膨脹發生的短部分,而不是一個長部分,這將更難處理)。
10.3 : 熱力學
[edit | edit source]10.3.1
[edit | edit source]熱力學用於描述熱力學系統不同部分中熱力學變數之間的關係。熱力學變數的主要例子是熱量、功和熵,但還有很多其他變數,如壓力、體積、表面張力、磁化率和(摩爾)濃度。所有這些變化都在系統內部和外部熱量、功和熵的傳遞背景下進行研究。經典熱力學完全關注平衡狀態,因此其方程中不出現帶有時間維度的量。只有時間的順序可能會出現(之前,之後)。64.134.223.225 (discuss) 02:08, 26 August 2014 (UTC)
10.3.2
[edit | edit source]熱量和功都是能量的形式,因此,加熱物體或對物體做功會導致能量的傳遞。A 對 B 做功,會增加 B 的內能,同時減少 A 的內能,依此類推。
10.3.3
[edit | edit source]熱力學中的系統是指具有特定內能的物體。
例如,一塊金屬塊就是一個系統。可以向其中加入熱量或從其中取出熱量。對它做功的概念有點模糊,但可以想象。
一定質量的氣體也可以是一個系統。熱量可以進出,如果你壓縮它,你就在做功(從而增加內能),如果氣體做功(即被允許膨脹,但推動活塞回來或其他情況),那麼它的內能就會減少。
熱力學過程是指從系統中取出或輸入熱量,或對系統做功或由系統做功的任何過程。
10.3.4
[edit | edit source]如果快速壓縮氣體,則其溫度會升高。壓縮氣體所做的功已轉換為內能。如果然後讓氣體冷卻,與功所提供的能量量相等的熱量將釋放到周圍環境中。
如果允許氣體膨脹,則會發生相反的情況。溫度(和內能)會降低,然後系統會從周圍環境中吸收熱量。換句話說,系統會做功(膨脹),導致內能損失,但如果讓系統這樣做,它會吸收回熱量。
功在第一種情況下轉換為熱量,熱量在第二種情況下轉換為功。
10.3.5
[edit | edit source]等溫 : 等溫過程是指內能(或溫度)沒有變化的過程。這種過程的一個例子可能是非常緩慢地膨脹或壓縮氣體,這樣在對系統做功或由系統做功時,會從周圍環境中吸收或釋放熱量。因此,即使做功並傳遞熱量,溫度也會保持恆定。在等溫過程中,所做的功和傳遞出去的熱量必須以相同的速度向相反的方向發生。
絕熱 : 絕熱過程是指 ΔQ 為零(即沒有熱量離開或進入系統)的過程。最常見的例子是快速壓縮或膨脹氣體,這樣就沒有時間傳遞熱量。在這樣的過程中,內能(即溫度)會在做功時發生變化。
等容 : 等容過程是指 ΔV 為零(即體積變化為零)的過程。在這樣的過程中,系統所做的功為零。一個例子是將只包含空氣的密閉錫罐放入火中。在第一近似中,罐子不會膨脹,唯一的變化是氣體獲得內能,這可以透過其溫度和壓力的升高來證明。在數學上,ΔQ = ΔU。
等壓 : 等壓過程是指壓力保持恆定的過程。一個簡單的例子是加熱一鍋沒有蓋子的水,這樣水錶面就會受到恆定壓力(大氣壓力)。
10.3.6
[edit | edit source]在 P-V 圖(壓力與體積)上說明這些熱力學過程是另一件事,如果使用圖表會更好。
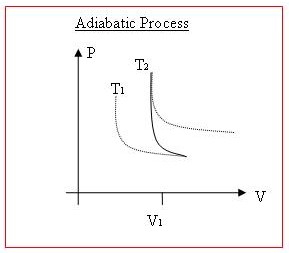
當對氣體做功或由氣體做功,或當熱量傳遞進或出氣體時,體積和壓力通常都會發生變化。P 與 V 圖上等溫線的曲線在 x 軸和 y 軸都有漸近線。溫度更高的曲線遠離原點。
等溫過程將完全遵循這些溫度曲線之一,因為內能是恆定的。
對於絕熱過程,當對系統做功時,溫度會升高,因此圖上的點會“向上”移動到更高的溫度曲線。如果由系統做功,則點會“向下”移動到更低的溫度曲線。
除此之外,P 與 V 圖上產生的曲線通常由過程的性質決定。有時只有壓力會發生變化(可以新增更多氣體,或者溫度可以發生變化),有時只有體積會發生變化(溫度會隨著體積減小而降低,保持壓力恆定)。
還值得注意的是(雖然我不知道是否必要),曲線下的面積等於系統所做的功(這在下一節中會變得令人困惑)。
10.3.7
[edit | edit source]ΔU = ΔQ + ΔW
這個方程將熱量和功的變化與內能的變化聯絡起來。實際符號有點棘手,但如果我們知道正 ΔU 值會導致溫度升高,就可以記住。基於此,我們知道透過向系統新增熱量,溫度會升高,因此當向系統新增熱量時,ΔQ 為正。
類似地,如果對系統做功,溫度會升高,因此對系統做功時,ΔW 為正。顯然,當熱量釋放到周圍環境中時,ΔQ 為負,當系統做功時,ΔW 為負。
這個方程可以透過代入兩個值並求出第三個值來應用。由於我們知道 ΔU 為零,因此這個方程可以在等溫過程中簡化,並且由於我們知道 ΔQ 為零,因此它可以在絕熱過程中簡化。
10.3.8
[edit | edit source]熱力學迴圈是指一系列熱力學過程最終使系統恢復到初始狀態,從該狀態可以重複該過程。這個概念被熱機所利用,熱機使用一系列重複的熱力學過程來從熱能產生機械能。熱機主要有兩種型別(內燃機和外燃機),下面將對它們進行描述。
外燃機 : 這些是老式的發動機,用於蒸汽火車。熱量用於將水煮沸,水變成蒸汽,從而增加管道中的壓力。這種壓力增加會迫使活塞向下移動(活塞連線到適合發動機正在做的事情的任何東西)。一旦它被完全壓下,一個閥門就會釋放,蒸汽被允許逸出到另一組管道中,最終透過冷凝器返回到鍋爐。這會降低壓力,活塞被其他活塞在凸輪軸中的作用或彈簧推回。當它再次到達頂部時,更多的蒸汽被允許進入,迫使活塞再次向下移動。也可以使用渦輪機,其中蒸汽用於旋轉渦輪機,從而產生旋轉運動(這通常用於發電)。我認為我們真正需要知道的就是這些,內燃機在這裡更重要。
內燃機:這是一種目前汽車中常用的發動機型別,汽油在汽缸內被點燃。它們被稱為四衝程發動機,因為整個過程發生在兩個迴圈中(兩次向上衝程和兩次向下衝程)。活塞從汽缸頂部開始向下移動。進氣門開啟,汽缸內吸入燃料和氧氣的混合物。當活塞到達底部時,進氣門關閉,活塞向上移動,壓縮混合物,直到活塞到達頂部。當活塞處於頂部時,火花塞點燃混合物,產生向下的高壓,推動活塞向下(這是發動機實際做功的地方)。當活塞到達底部時,排氣門開啟,活塞向上移動時排出廢氣。到達頂部後,排氣門關閉,進氣門開啟(回到起點)。所有這些過程都可以用 P-V 圖表示(有人想畫一個嗎?)。大多數物理教科書中會有一個類似的圖表。
熵(符號 S)是衡量系統混亂程度的指標。關於機率、亞態和資訊理論,有一個複雜的解釋,但我認為沒有必要。基本上,熵總是增加的。在一個系統中可以降低熵,但它會導致該系統周圍環境的熵增加。這是熱力學第二定律;自然系統趨向於向更混亂的狀態發展。從能量的角度來看,混亂程度的增加意味著能量分佈更均勻。如果有一個高能量點和一個低能量點,可以使用這兩個點之間的能量差做功,熵會降低這種能量差。換句話說,能量趨於均勻分佈,而不是集中在一個點上。
自然系統趨向於向更混亂的狀態發展(熱力學第二定律)。這意味著你無法制造出一種發動機,它可以將輸入到它的能量的 100% 轉換為功(即,沒有發動機可以達到 100% 的效率)。例如,第一定律表明,放在桌子上的木塊可以將其熱能的一部分轉換為功,並從桌子上跳下來,但第二定律說這不可能發生(不是說它不能發生,只是它非常非常不可能)。
此外,由於它不適合放在任何其他地方,但出現在資料手冊中,方程 ΔS = ΔQ/ΔT 可以用來求解熵的變化(其中 Q = 熱量,T = 溫度)。這實際上是一個微積分方程,但對於 T 的微小變化,用平均溫度近似就足夠了。
冰箱:基本原理是透過做功克服熵,在內部產生一個低溫區域,而在外部產生一個高溫區域。這個過程透過一套沿著系統外壁和內壁執行的管道來實現。低壓(因此冷)氣體透過內壁管道,吸收冰箱內部的熱量。然後,使用冷凝器(活塞)對該氣體進行加壓,並透過外壁管道進行抽送。由於該氣體進行了做功,熱量從該氣體釋放到冰箱外部。然後,慢慢地讓氣體透過連線到低壓管道的閥門進行再迴圈。這樣,即使內部溫度已經很低,熱量還是從內部轉移到外部。這似乎違反了第二定律,但宇宙的總熵實際上正在增加,因為讓它發生需要能量(驅動冷凝器)。這種系統的效率由方程 效率 = QH-QL / QL 定義,其中效率是指冰箱的效率(1 表示完美或 100% 效率),QL 是低溫(內部)溫度,QH 是高溫(外部)溫度。
熱泵:熱泵是一種特殊的加熱器,通常與 HVAC 系統中的空調功能一起安裝,當預期的氣候變化使其比安裝和使用直接加熱器更經濟時。熱泵不是依靠熱量的純粹產生,而是將熱量(更準確地說,是熱能)從一個地方轉移到另一個地方。熱泵的工作原理是透過做功將熱量從寒冷的外部轉移到溫暖的內部。這與上面描述的冰箱正好相反。這種泵的效率將為 效率 = QH-QL / QH,與上述工作原理相同。
請注意,在每種情況下,這個方程都類似於資料手冊中的方程,但分母必須根據特定過程要實現的目標進行選擇。
如果我們想從哲學角度看待問題,可以將熵視為定義時間的“向前”和“向後”的因素。隨著時間的推移,熵增加,因此我們可以將時間視為熵增加時向前推進。如上所述,熱泵和冰箱能夠降低系統中的熵,但會增加整個系統 + 環境的熵。當冰(或其他東西)融化時,它會吸收熱量,因此熵會增加。從固態到液態到氣態的轉變也標誌著熵的增加,因為粒子變得越來越隨機地運動。