無機化學/化學鍵/軌道雜化

四個sp³軌道。

三個sp²軌道。

在化學中，雜化（或雜交）是將原子軌道混合成新的雜化軌道的概念，這些軌道適用於電子配對以形成價鍵理論中的化學鍵。雜化軌道在解釋分子幾何形狀和原子鍵合特性方面非常有用。

歷史和用途

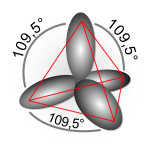
化學家萊納斯·鮑林首先發展了雜化理論，以解釋甲烷（CH₄）等分子的結構。鮑林指出，碳原子透過使用一個s軌道和三個p軌道形成四個鍵，因此“可以推斷”碳原子將使用p軌道形成三個直角鍵，並使用s軌道在某個任意方向形成第四個較弱的鍵。然而，實際上，甲烷具有四個強度相等的鍵，它們之間以109.5°的四面體鍵角分開。鮑林解釋說，在存在四個氫原子的情況下，s和p軌道形成了四個等價的組合或雜化軌道，每個軌道都用sp³表示以指示其組成，這些軌道沿四個C-H鍵方向排列。從歷史上看，這個概念是為這種簡單的化學體系而發展的，但後來該方法被更廣泛地應用，如今它被認為是合理化有機化合物結構的有效啟發式方法。它給出了一個與路易斯結構等價的簡單軌道影像。雜化理論主要用於有機化學。

雜化理論是有機化學的一個組成部分。對於繪製反應機理，有時需要一個經典的鍵合影像，其中兩個原子共享兩個電子。雜化理論解釋了烯烴和甲烷中的鍵合。主要由軌道雜化決定的p特性或s特性的數量可用於可靠地預測分子性質，例如酸度或鹼度。

概述

軌道是電子在分子中行為的模型表示。在簡單雜化的例子中，這種近似基於原子軌道，類似於氫原子獲得的那些，氫原子是唯一一個對其薛定諤方程有精確解析解的原子。在較重的原子（如碳、氮和氧）中，使用的原子軌道是2s和2p軌道，類似於氫的激發態軌道。

假設雜化軌道是原子軌道的混合物，以不同的比例疊加在一起。例如，在甲烷中，形成每個C-H鍵的C雜化軌道包含25%的s特性和75%的p特性，因此被稱為sp³（讀作s-p-three）雜化。量子力學將這種雜化描述為形式為N[s + (√3)pσ]的sp³波函式，其中N是歸一化常數（此處為1/2），pσ是沿C-H軸方向的p軌道，形成σ鍵。p與s的比率（一般用λ表示）在此示例中為√3，N²λ² = 3/4為p特性或p分量的權重。

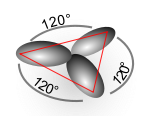
通常情況下，同一原子上的任意兩個雜化軌道都必須相互正交。對於一個原子，其s和p軌道形成雜化軌道h_i和h_j，夾角為$\theta$，正交條件意味著以下關係：1 + $\lambda$_i$\lambda$_j cos($\theta$) = 0。雜化軌道i的p-s比為$\lambda$_i²，雜化軌道j的p-s比為$\lambda$_j²。正如Bent規則所述，指向更具電負性的取代基的鍵往往具有更高的p特性。在同一原子上的等價雜化軌道的特殊情況下，同樣夾角為$\theta$，該方程簡化為1 + $\lambda$² cos($\theta$) = 0。例如，BH₃具有三角平面幾何形狀，三個120°鍵角，硼原子周圍有三個等價雜化軌道，因此1 + $\lambda$² cos($\theta$) = 0 變為 1 + $\lambda$² cos(120°) = 0，得到$\lambda$² = 2 作為p-s比。換句話說，sp²雜化。

雜化型別

sp³

對於四面體配位的碳（例如，甲烷CH₄），碳應該有4個軌道，具有正確的對稱性來與4個氫原子成鍵。

碳的基態電子構型為1s² 2s² 2p²，或者更容易理解為

C	↑↓	↑↓	↑	↑
	1s	2s	2p	2p	2p

（注意：1s軌道的能量低於2s軌道，2s軌道的能量低於2p軌道）

碳原子可以使用其兩個單佔據的p型軌道與兩個氫原子形成兩個共價鍵，生成亞甲基CH₂單線態，這是卡賓中最簡單的例子。碳原子還可以透過將一個電子從雙佔據的2s軌道激發到空的2p軌道，從而形成四個單佔據軌道，與四個氫原子成鍵。

C*	↑↓	↑	↑	↑	↑
	1s	2s	2p	2p	2p

形成兩個額外部索引鍵釋放的能量超過了所需的激發能，在能量上更有利於形成四個C-H鍵。

從量子力學的角度來看，如果四個鍵是等價的，則可以獲得最低的能量，這需要它們是由碳上的等價軌道形成的。可以得到一組四個等價軌道，它們是價層（核心軌道幾乎從未參與成鍵）s和p波函式的線性組合，即四個sp³雜化軌道。

C*	↑↓	↑	↑	↑	↑
	1s	sp3	sp3	sp3	sp3

在CH₄中，四個sp³雜化軌道與氫的1s軌道重疊，生成四個σ（西格瑪）鍵（即四個長度和強度相同的單共價鍵）。

轉化為

sp²

其他碳基化合物和其他分子可以用類似甲烷的方式解釋。例如，乙烯 (C₂H₄) 在兩個碳原子之間有一個雙鍵。其路易斯結構如下所示

乙烯的路易斯結構。每個碳原子與兩個氫原子鍵合，碳原子之間有一個雙鍵。

對於該分子，碳原子進行sp²雜化，因為碳原子之間的雙鍵需要一個π鍵，並且每個碳原子只形成三個σ鍵。在sp²雜化中，2s軌道只與三個可用的2p軌道中的兩個混合

C*	↑↓	↑	↑	↑	↑
	1s	sp2	sp2	sp2	2p

形成總共三個sp²軌道和一個剩餘的p軌道。在乙烯中，兩個碳原子透過兩個sp²軌道的重疊形成σ鍵，並且每個碳原子透過s–sp²重疊與氫形成兩個共價鍵，所有鍵角均為120°。碳原子之間垂直於分子平面的π鍵由2p–2p重疊形成。氫-碳鍵的強度和長度都相等，這與實驗資料相符。

sp

諸如炔烴之類的具有三鍵的化合物的化學鍵合可以透過sp雜化來解釋。在這個模型中，2s軌道只與三個p軌道中的一個混合，

C*	↑↓	↑	↑	↑	↑
	1s	sp	sp	2p	2p

產生兩個sp軌道和兩個剩餘的p軌道。乙炔 (C₂H₂) 的化學鍵合包括兩個碳原子之間的sp–sp重疊形成σ鍵，以及由p–p重疊形成的兩個額外的π鍵。每個碳原子還以180°角的σs–sp重疊與氫鍵合。

雜化和分子形狀

雜化有助於解釋分子形狀，因為鍵之間的角度（大約）等於雜化軌道之間的角度。

不同型別的雜化軌道的形狀

sp^x雜化

由於主族元素的價電子軌道是一個s軌道和三個p軌道，並遵循相應的八隅體規則，因此sp^x雜化用於模擬這些分子的形狀。

配位數	形狀	雜化	例子
2	線性	sp雜化 (180°)	CO2
3	平面三角形	sp2雜化 (120°)	BCl3
4	四面體	sp3雜化 (109.5°)	CCl4
軌道間角	$\theta =\arccos \left(-{\frac {1}{x}}\right)$

sp^xd^y雜化

由於過渡金屬的價電子軌道是五個d軌道、一個s軌道和三個p軌道，並遵循相應的18電子規則，因此sp^xd^y雜化用於模擬這些分子的形狀。由於涉及不同的d軌道，這些分子往往具有對應於相同雜化的多種形狀。由於p軌道不一定完全佔據，因此平面正方形形狀具有16個價電子。

配位數	形狀	雜化	例子
4	平面正方形	sp2d雜化	PtCl42−
5	三角雙錐	sp3d雜化	Fe(CO)5
	四方錐		MnCl52−
6	八面體	sp3d2雜化	Mo(CO)6
7	五角雙錐	sp3d3雜化	ZrF73−
	頂帽八面體		MoF7−
	頂帽三角稜柱		TaF72−
8	四方反稜柱	sp3d4雜化	ReF8−
	十二面體		Mo(CN)84−
	雙頂帽三角稜柱		ZrF84−
9	三頂帽三角稜柱	sp3d5雜化	ReH92−
	頂帽四方反稜柱

sd^x雜化

在某些d電子數低的過渡金屬配合物中，p軌道未被佔據，並且sd^x雜化用於模擬這些分子的形狀。

配位數	形狀	雜化	例子
3	三角錐形	sd2雜化 (90°)	CrO3
4	四面體	sd3雜化 (70.5°, 109.5°)	TiCl4
5	四方錐	sd4雜化 (65.9°, 114.1°)	Ta(CH3)5
6	C3v 三角稜柱	sd5雜化 (63.4°, 116.6°)	W(CH3)6
軌道間角	$\theta =\arccos \left(\pm {\sqrt {{\frac {1}{3}}\left(1-{\frac {2}{x}}\right)}}\right)$

超價分子的雜化

八隅體擴充套件

在一些普通化學教科書中，使用保林首先提出的“擴充套件八隅體”方案，利用d軌道來呈現主族AX₅及以上化合物的雜化。然而，鑑於計算化學計算的結果，這種方案現在被認為是不正確的。

配位數	形狀	雜化	例子
5	三角雙錐	sp3d雜化	PF5
6	八面體	sp3d2雜化	SF6
7	五角雙錐	sp3d3雜化	IF7

1990年，Magnusson發表了一篇具有開創性的著作，明確排除了d軌道雜化在第二週期元素超價化合物鍵閤中的作用。長期以來，在使用分子軌道理論描述這些分子時，這是一個有爭議和令人困惑的問題。這裡部分混淆源於這樣一個事實，即必須在用於描述這些化合物的基組中包含d函式（否則會導致不合理的能量和扭曲的幾何形狀），並且d函式對分子波函式的貢獻很大。歷史上，這些事實被解釋為意味著d軌道必須參與鍵合。然而，Magnusson在他的著作中得出結論，d軌道的參與與超價無關。

共振

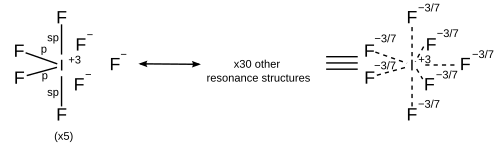
根據計算化學，更好的處理方法是除了雜化之外，還要引入σ鍵共振，這意味著每個共振結構都有其自身的雜化方案。所有共振結構都必須遵循八隅體規則。

配位數	共振結構
5	三角雙錐
6	八面體
7	五角雙錐

計算VB理論中的雜化

雖然軌道雜化的簡單模型常用於解釋分子形狀，但在現代價鍵程式中，雜化的使用方法有所不同。具體來說，雜化不是先驗確定的，而是透過變分最佳化來尋找最低能量解，然後進行報告。這意味著所有人為的約束，特別是兩個約束，都被取消了

• 雜化被限制為整數（等價雜化）
• 雜化軌道彼此正交（雜化缺陷）

這意味著在實踐中，雜化軌道並不符合通常教授的簡單概念，因此在科學計算論文中，為了表達它們的性質，通常簡單地將其稱為sp^x、sp^xd^y或sd^x雜化，而不是更具體的整數數值。

等價雜化

儘管理想的雜化軌道很有用，但實際上大多數鍵需要中間性質的軌道，類似於中間離子-共價特性。這需要擴充套件以包含每種型別（s、p、d）原子軌道的靈活權重，並在分子幾何形狀偏離理想鍵角時，允許對鍵形成進行定量描述。p成分的含量不受限於整數；即，sp^2.5之類的雜化也很容易描述。

鍵軌道的雜化由Bent規則決定：“原子s成分集中在指向正電性取代基的軌道上”。

對於具有孤對電子的分子，成鍵軌道是等價的sp^x雜化。例如，水中氧的兩個成鍵雜化軌道可以描述為sp^4.0，以得到104.5°的軌道間角。這意味著它們具有20%的s成分和80%的p成分，並且不意味著雜化軌道是由氧原子上的一個s軌道和四個p軌道形成的，因為氧的2p亞層僅包含三個p軌道。

雜化缺陷

s和p軌道雜化形成有效的sp^x雜化需要它們具有相當的徑向範圍。雖然2p軌道的平均尺寸比2s軌道大不到10%，部分原因是2p軌道缺乏徑向節點，但具有一個徑向節點的3p軌道比3s軌道大20-33%。s和p軌道的範圍差異在同一族中進一步增加。可以透過考慮局域分子軌道來分析化學鍵中原子的雜化，例如在自然鍵軌道（NBO）方案中使用自然局域分子軌道。在甲烷CH₄中，計算出的p/s比率約為3，與“理想”sp³雜化一致，而對於矽烷SiH₄，p/s比率更接近於2。其他2p元素也觀察到類似的趨勢。用氟取代氫進一步降低了p/s比率。2p元素表現出接近理想的雜化，具有正交的雜化軌道。對於較重的p區元素，不能證明這種正交性的假設。庫澤爾尼格將這些與理想雜化的偏差稱為雜化缺陷。

然而，Gerratt、Cooper和Raimondi（SCVB）以及Shaik和Hiberty（VBSCF）等計算VB小組更進一步地論證，即使對於甲烷、乙烯和乙炔等模型分子，雜化軌道也已經存在缺陷且非正交，例如甲烷的雜化是sp^1.76而不是sp³。

光電子能譜

關於軌道雜化的一個誤解是，它錯誤地預測了許多分子的紫外光電子能譜。雖然如果將庫普曼斯定理應用於局域雜化，這是正確的，但量子力學要求（在這種情況下是離子化的）波函式服從分子的對稱性，這意味著價鍵理論中的共振。例如，在甲烷中，離子化態（CH₄⁺）可以由四個共振結構構成，將彈出的電子歸因於四個sp³軌道中的每一個。這四個結構的線性組合，保持結構數量不變，導致三倍簡併的T₂態和一個A₁態。離子化態與基態之間的能量差將是電離能，這會產生兩個與實驗一致的值。

存在兩種不同的CH₄⁺態（A₁和T₂），它們都是由CH₄的電離產生的。這導致了甲烷光電子能譜上的兩個獨特峰。

局域MOs與正則MOs

由雜化原子軌道形成的成鍵軌道可以被認為是局域分子軌道，可以透過適當的數學變換，由分子軌道理論的離域軌道形成。對於基態分子，軌道的這種變換不會改變總的多電子波函式。因此，基態的雜化軌道描述與基態總能量和電子密度以及對應於最小總能量值的分子幾何形狀的離域軌道描述等價。

兩種局域表示

H₂O的對稱性適應和雜化的孤對電子

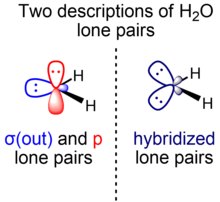
具有多重鍵或多個孤對電子的分子可以具有用σ和π對稱性或等價軌道表示的軌道。不同的價鍵方法使用兩種表示方法中的任何一種，它們具有數學上等價的總多電子波函式，並且透過佔據分子軌道集的酉變換相關聯。

對於多重鍵，σ-π表示法比等價軌道（彎曲鍵）表示法更為普遍。相反，對於多個孤對電子，大多數教科書使用等價軌道表示法。但是，σ-π表示法也使用，例如Weinhold和Landis在自然鍵軌道的背景下使用，自然鍵軌道是一種局域軌道理論，包含經典（價鍵/路易斯結構）成鍵對和孤對的現代化類似物。例如，對於氟化氫分子，兩個F孤對電子本質上是未雜化的p軌道，而另一個是sp^x雜化軌道。類似的考慮適用於水（一個O孤對電子位於純p軌道中，另一個位於sp^x雜化軌道中）。