跳轉到內容

無機化學/化學鍵/VSEPR理論

Add links
來自華夏公益教科書，開放的書籍，開放的世界
< 無機化學 | 化學鍵
最新修訂版本於2022年4月10日審查。有模板/檔案更改正在等待審查。

價層電子對互斥理論（VSEPR）是一個化學模型，用於根據中心原子周圍的電子對數量來預測單個分子的幾何形狀。[1] 它也被稱為吉萊斯皮-尼霍爾姆理論，以其兩位主要開發者羅納德·吉萊斯皮和羅納德·尼霍爾姆命名。

VSEPR理論的前提是，原子周圍的價層電子對傾向於相互排斥，因此它們將採用一種使這種排斥最小化的排列方式。這反過來又降低了分子的能量並增加了其穩定性，從而決定了分子的幾何形狀。

歷史

[編輯 | 編輯原始碼]

分子幾何形狀與價層電子數（包括共用電子對和非共用電子對）之間相關性的想法，最早由內維爾·西德威克和赫伯特·鮑威爾於 1940 年在牛津大學的貝克萊恩演講中提出。[2] 1957 年，倫敦大學學院的羅納德·吉萊斯皮和羅納德·西德尼·尼霍爾姆完善了這一概念，建立了一個更詳細的理論，能夠在各種替代幾何形狀之間進行選擇。[3][4]

概述

[編輯 | 編輯原始碼]

VSEPR 理論用於預測分子中中心原子周圍電子對的排列方式，尤其是簡單對稱的分子。在本理論中，中心原子被定義為與兩個或多個其他原子鍵合的原子，而末端原子僅與另一個原子鍵合。[5]:398 例如，在異氰酸甲酯 (H3C-N=C=O) 分子中，兩個碳和一個氮是中心原子，而三個氫和一個氧是末端原子。[5]:416 中心原子的幾何形狀及其非鍵合電子對反過來又決定了整個分子更大結構的幾何形狀。

中心原子價層電子對的數量是在繪製分子的路易斯結構之後確定的，並將路易斯結構擴充套件以顯示所有鍵合基團和孤對電子。[5]:410–417 在 VSEPR 理論中，雙鍵或三鍵被視為單個鍵合基團。[5] 中心原子鍵合的原子數與中心原子非鍵合價電子形成的孤對數之和稱為中心原子的空間數。

電子對（如果存在多重鍵，則為基團）被認為位於以中心原子為中心的球體的表面上，並且傾向於佔據位置，以最大限度地減小它們之間的相互排斥，從而最大限度地增加它們之間的距離。[5]:410–417[6] 因此，電子對（或基團）的數量決定了它們將採用的整體幾何形狀。例如，當中心原子周圍有兩個電子對時，它們之間的相互排斥在它們位於球體的相對兩極時最小。因此，中心原子預計將採用線性幾何形狀。如果中心原子周圍有 3 個電子對，它們的排斥可以透過將它們放置在以原子為中心的等邊三角形的頂點上以最小化。因此，預測的幾何形狀是三角形。同樣，對於 4 個電子對，最佳排列是四面體。[5]:410–417

作為預測給定數量的電子對所採用的幾何形狀的工具，一種經常使用的是利用充氣的氣球來物理演示最小電子對排斥原理。透過操作，氣球會獲得輕微的表面靜電荷，這會導致它們在將它們綁在一起時採用與相應數量的電子對大致相同的幾何形狀。例如，五個綁在一起的氣球將採用三角雙錐體幾何形狀，就像 PCl5 分子的五個鍵合對一樣。

空間數

[編輯 | 編輯原始碼]
四氟化硫的空間數為 5。

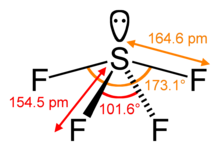
分子中中心原子的空間數是與該中心原子鍵合的原子數，稱為配位數，加上中心原子上的孤對價電子數。[7] 例如，在 SF4 分子中，中心硫原子有四個配體；硫的配位數為 4。除了四個配體外，硫在這個分子中還有一個孤對。因此，空間數為 4 + 1 = 5。

排斥程度

[編輯 | 編輯原始碼]

整體幾何形狀透過區分鍵合和非鍵合電子對進一步細化。在與相鄰原子形成σ鍵中共享的鍵合電子對比該原子的非鍵合（孤對）電子對更遠離中心原子，非鍵合電子對靠近其帶正電荷的原子核。因此，VSEPR 理論認為孤對的排斥大於鍵合對的排斥。因此，當一個分子具有 2 種不同排斥程度的相互作用時，VSEPR 理論預測結構，其中孤對佔據允許它們經歷較少排斥的位置。孤對 - 孤對 (lp–lp) 排斥被認為比孤對 - 鍵合對 (lp–bp) 排斥更強，而孤對 - 鍵合對 (lp–bp) 排斥被認為比鍵合對 - 鍵合對 (bp–bp) 排斥更強，這些區別指導關於整體幾何形狀的決定，當 2 個或多個非等效位置是可能的時。[5]:410–417 例如，當 5 個價層電子對圍繞中心原子時，它們將採用三角雙錐體分子幾何形狀，具有兩個共線的軸向位置和三個赤道位置。軸向位置的電子對只有三個相鄰的赤道對，距離只有 90°，而第四個對距離 180° 遠得多，而赤道電子對只有兩個相鄰對在 90° 處，兩個在 120° 處。來自距離 90° 的近鄰對的排斥更為重要，因此軸向位置經歷的排斥比赤道位置更多；因此，當存在孤對時，它們傾向於佔據赤道位置，如下一節中針對空間數為 5 的示意圖所示。[6]

孤對電子和成鍵電子之間的差異也可以用來解釋理想幾何形狀的偏差。例如，H2O 分子在其價層中有四個電子對：兩個孤對電子和兩個成鍵電子對。這四個電子對分佈開來，大致指向四面體的頂點。然而，兩個 O-H 鍵之間的鍵角只有 104.5°，而不是規則四面體的 109.5°，因為兩個孤對電子（其密度或機率包絡更靠近氧原子核）比兩個成鍵電子對施加更大的相互排斥。[5]:410–417[6]

具有較高鍵序的鍵也施加更大的排斥力，因為 π 鍵電子參與其中。[6] 例如，在異丁烯 (H3C)2C=CH2 中，H3C-C=C 角 (124°) 大於 H3C-C-CH3 角 (111.5°)。然而，在碳酸根離子 CO2−3 中，由於共振，所有三個 C-O 鍵都是等效的，角度為 120°。

AXE 方法

[edit | edit source]

在應用 VSEPR 理論時，通常使用電子計數的“AXE 方法”。中心原子周圍的電子對用公式 AXnEm 表示，其中 A 代表中心原子，總是隱含下標 1。每個 X 代表一個配體（與 A 鍵合的原子）。每個 E 代表中心原子上的一個孤對電子。[5]:410–417 X 和 E 的總數稱為空間位阻數。例如，在分子 AX3E2 中，原子 A 的空間位阻數為 5。

當取代基 (X) 原子不完全相同時，幾何形狀仍然大致有效，但鍵角可能與所有外部原子都相同的鍵角略有不同。例如，烯烴如 C2H4 中的雙鍵碳是 AX3E0，但鍵角並不完全都是 120°。同樣，SOCl2 是 AX3E1，但由於 X 取代基並不相同，因此 X-A-X 角並不完全相等。

根據空間位阻數以及 X 和 E 的分佈，VSEPR 理論做出了以下表格中的預測。

主族元素

[edit | edit source]

對於主族元素，存在立體化學活性孤對電子 E，其數量可以在 0 到 3 之間變化。請注意，幾何形狀是根據原子位置而不是電子排列命名的。例如，將 AX2E1 描述為彎曲分子意味著三個原子 AX2 不在一條直線上，儘管孤對電子有助於確定幾何形狀。

空間位阻
數		 分子幾何形狀[8]
0 個孤對電子		 分子幾何形狀[5]:413–414
1 個孤對電子		 分子幾何形狀[5]:413–414
2 個孤對電子		 分子幾何形狀[5]:413–414
3 個孤對電子
2
線性
      
3
平面三角形
彎曲
    
4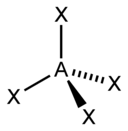
四面體
三角錐形
彎曲
  
5
三角雙錐
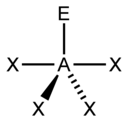蹺蹺板
T 形
線性
6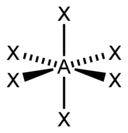
八面體
四方錐形
平面四方
  
7
五角雙錐
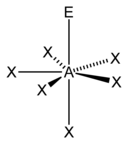五角錐形
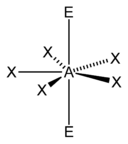五角平面
  
8
四方反稜柱
 		    
分子
型別		 形狀[5]:413–414 電子排列[5]:413–414
包括孤對電子，以淺黃色顯示 		幾何形狀[5]:413–414
不包括孤對電子 		示例
AX2E0 線性 BeCl2,[1] CO2[6]
AX2E1 彎曲 NO2-,[1] SO2,[5]:413–414 O3,[1] CCl2
AX2E2 彎曲 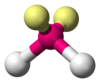H2O,[5]:413–414 OF2[9]:448
AX2E3 線性 XeF2,[5]:413–414 I3-,[9]:483 XeCl2
AX3E0 平面三角形 BF3,[5]:413–414 CO2−3,[9]:368 NO3-,[1] SO3[6]
AX3E1 三角錐形 NH3,[5]:413–414 PCl3[9]:407
AX3E2 T 形 ClF3,[5]:413–414 BrF3[9]:481
AX4E0 四面體 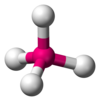CH4,[5]:413–414 PO3−4, SO2−4,[6] ClO4-,[1] XeO4[9]:499
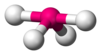
AX4E1 蹺蹺板或雙錐 SF4[5]:413–414[9]:45
AX4E2 平面四方 XeF4[5]:413–414
AX5E0 三角雙錐 PCl5[5]:413–414
AX5E1 四方錐形 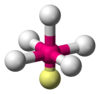ClF5,[9]:481 BrF5,[5]:413–414 XeOF4[6]
AX5E2 五角平面 XeF5-[9]:498
AX6E0 八面體 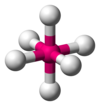SF6[5]:413–414
AX6E1 五角錐形 XeOF5-,[10] IOF2−5[10]
AX7E0 五角雙錐[6] IF7[6]
AX8E0 正方形反稜柱[6] IF8-

過渡金屬（Kepert 模型）

[edit | edit source]

過渡金屬原子上的孤對電子通常是立體化學惰性的，這意味著它們的存在不會改變分子幾何形狀。例如，六水合配合物 M(H2O)6 對 M = V3+, Mn3+, Co3+, Ni2+ 和 Zn2+ 都是八面體形的，儘管中心金屬離子的電子構型分別是 d2, d4, d6, d8 和 d10。 [9]:542 Kepert 模型忽略了過渡金屬原子上的所有孤對電子，因此所有這些原子的周圍幾何形狀對應於 AXn 的 VSEPR 幾何形狀，其中有 0 個孤對電子 E。 [11][9]:542 這通常寫成 MLn，其中 M = 金屬，L = 配體。Kepert 模型預測了配位數為 2 到 9 的以下幾何形狀

分子
型別		 形狀 幾何形狀 示例
ML2 線性 HgCl2[1]
ML3 平面三角形
ML4 四面體 NiCl2−4
ML5 三角雙錐 Fe(CO)5
四方錐形 MnCl52−
ML6 八面體 WCl6[9]:659
ML7 五角雙錐形[6] ZrF3−7
帽狀八面體 MoF7-
帽狀三角稜柱 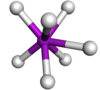TaF2−7
ML8 正方形反稜柱[6] ReF8-
十二面體 Mo(CN)4−8
雙帽狀三角稜柱 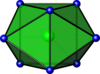ZrF4−8
ML9 三帽狀三角稜柱 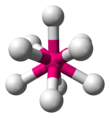ReH2−9[9]:254
帽狀正方形反稜柱

示例

[edit | edit source]

甲烷分子 (CH4) 是四面體形的，因為它有四對電子。四個氫原子位於四面體的頂點，鍵角為 cos−1(−1⁄3) ≈ 109° 28′。 [12][13] 這被稱為 AX4 型分子。如上所述，A 代表中心原子，X 代表外原子。 [5]:410–417

氨分子 (NH3) 有三對參與鍵合的電子，但氮原子上有一對孤對電子。 [5]:392–393 它沒有與其他原子鍵合；然而，它透過排斥作用影響著整體形狀。如上所述的甲烷，有四個電子密度的區域。因此，電子密度的區域的整體方向是四面體形的。另一方面，只有三個外原子。這被稱為 AX3E 型分子，因為孤對電子用 E 表示。 [5]:410–417 根據定義，分子形狀或幾何形狀僅描述原子核的幾何排列，對 NH3 而言為三角錐形。 [5]:410–417

7 或更高的空間數是可能的，但不太常見。空間數 7 發生在七氟化碘 (IF7) 中；空間數為 7 的基本幾何形狀是五角雙錐形。 [6] 空間數為 8 的最常見幾何形狀是正方形反稜柱幾何形狀。 [14]:1165 例如，八氰合鉬酸鹽 (Mo(CN)4−8) 和八氟合鋯酸鹽 (ZrF4−8) 陰離子。 [14]:1165 鉀九氫合錸酸鹽中的九氫合錸酸根離子 (ReH2−9) 是具有空間數為 9 的化合物的罕見例子，它具有三帽狀三角稜柱幾何形狀。 [9]:254[14]

空間數為 10、11、12 或 14 的可能幾何形狀分別是雙帽狀正方形反稜柱（或雙帽狀十二面體）、十八面體、二十面體和雙帽狀六角反稜柱。沒有化合物具有涉及單齒配體的這種高空間數，而涉及多齒配體的化合物通常可以更簡單地分析為具有較低空間數的配合物，當一些多齒配體被視為一個單元時。 [14]:1165,1721

例外

[edit | edit source]

有一些化合物組，VSEPR 無法預測正確的幾何形狀。

一些 AX2E0 分子

[edit | edit source]

較重 14 族元素炔烴類似物（RM≡MR，其中 M = Si、Ge、Sn 或 Pb）的形狀經計算為彎曲的。 [15][16][17]

一些 AX2E2 分子

[edit | edit source]

一個例子是氧化鋰分子 Li2O，它是線性的而不是彎曲的，這歸因於鍵合本質上是離子性的，導致鋰原子之間發生強烈的排斥作用。 [18]
另一個例子是 O(SiH3)2，其 Si-O-Si 角為 144.1°，與 Cl2O (110.9°)、(CH3)2O (111.7°) 和 N(CH3)3 (110.9°) 中的角度相比。Gillespie 的解釋是，當配體具有與中心原子相似或大於中心原子的電負性時，孤對電子的定位最強，因此它們排斥其他電子對的能力也最強。[19] 當中心原子電負性更強時，如 O(SiH3)2 中，孤對電子定位較差，排斥作用較弱。這一事實，加上更強的配體-配體排斥力（-SiH3 相比於上面的例子是一個相對較大的配體），導致了比預期更大的 Si-O-Si 鍵角。[19]

一些 AX6E1 和 AX8E1 分子

[edit | edit source]
六氟化氙，具有扭曲的八面體幾何結構

一些 AX6E1 分子，例如六氟化氙 (XeF6) 和 Te(IV) 和 Bi(III) 陰離子，TeCl2−6，TeBr2−6，BiCl3−6，BiBr3−6 和 BiI3−6，是八面體而不是五角錐體，孤對電子對幾何形狀的影響程度不如 VSEPR 預測的那樣。[20] 一種解釋是，配體的空間擁擠不允許非鍵合孤對電子存在；[19] 另一種解釋是惰性電子對效應。[21] 同樣地，八氟合氙酸根離子 (XeF2−8) 在亞硝醯八氟合氙(VI) 中[9]:498[22][23] 是一個正方反稜柱，而不是一個雙頂三角稜柱（如 VSEPR 理論預測的 AX8E1 分子），儘管它有一個孤對電子。

平面正方形 ML4 配合物

[edit | edit source]

Kepert 模型預測 ML4 過渡金屬分子呈四面體形狀，它無法解釋平面正方形配合物的形成。[9]:542 大多數此類配合物表現出 d8 電子構型，例如四氯合鉑酸根 (PtCl2−4) 離子。平面正方形配合物形狀的解釋涉及電子效應，需要使用晶體場理論。[9]:562-4

具有強 d 電子貢獻的配合物

[edit | edit source]
六甲基鎢，一個幾何結構不同於主族配位的過渡金屬配合物。

一些 d 電子數較少的過渡金屬配合物具有不尋常的幾何結構，這可以歸因於 d 亞層鍵合相互作用。[24] Gillespie 發現這種相互作用產生鍵合對，這些鍵合對也佔據了球體的相應對位點（與配體相對）。[25][26] 這種現象是由於 sdx 雜化軌道雙葉形結構導致的電子效應。[27][28] 這些鍵合對的排斥導致了一組不同的形狀。

分子型別 形狀 幾何形狀 示例
ML2 彎曲 VO+2
ML3 三角錐形 CrO3
ML4 四面體 TiCl4[9]:598–599
ML5 四方錐形 Ta(CH3)5[29]
ML6 C3v 三角稜柱 W(CH3)6[30]

第二主族較重元素 (即鈣、鍶和鋇鹵化物，MX2) 的三原子鹵化物的氣相結構並非如預測的那樣是線性的，而是彎曲的 (近似 X–M–X 角：CaF2，145°；SrF2，120°；BaF2，108°；SrCl2，130°；BaCl2，115°；BaBr2，115°；BaI2，105°)。[31] Gillespie 提出，這也是由於配體與金屬原子 d 亞層的鍵合相互作用導致的，從而影響了分子幾何形狀。[19][32]

奇電子分子

[edit | edit source]

VSEPR 理論可以擴充套件到具有奇數個電子的分子，方法是將未配對電子視為“半個電子對”。實際上，奇電子對幾何形狀的影響類似於完整的電子對，但影響較小，因此幾何形狀可能介於具有完整電子對的分子和中心原子少一個電子對的分子之間。

例如，二氧化氮 (NO2) 是一個 AX2E0.5 分子，中心氮原子有一個未配對電子。VSEPR 預測的幾何形狀類似於 NO2- 離子 (AX2E1，彎曲，鍵角約為 120°)，但介於 NO2- 和 NO+2 (AX2E0，線性，180°) 之間。實際上，NO2 是彎曲的，角度為 134°，更接近 120° 而不是 180°，這與理論定性一致。

同樣地，二氧化氯 (ClO2，AX2E1.5) 的幾何形狀類似於 ClO2-，但介於 ClO2- 和 ClO+2 之間。

最後，甲基自由基 (CH3) 預計像甲基陰離子 (CH3-) 一樣是三角錐形的，但鍵角更大，如同三角平面甲基陽離子 (CH+3)。然而，在這種情況下，VSEPR 預測並不完全正確，因為 CH3 實際上是平面的，儘管它扭曲成三角錐形幾何結構只需要很少的能量。[33]

參考文獻

[edit | edit source]
  1. ↑ a b c d e f g Jolly, W. L. (1984). 現代無機化學. McGraw-Hill. pp. 77–90. ISBN 978-0-07-032760-3.
  2. ↑ http://rspa.royalsocietypublishing.org/content/176/965/153.abstract N.V.Sidgwick 和 H.M.Powell, Proc.Roy.Soc.A 176, 153–180 (1940) Bakerian 講座。立體化學型別和價鍵組
  3. ↑ R.J.Gillespie 和 R.S.Nyholm, Quart.Rev. 11, 339 (1957)
  4. ↑ R.J.Gillespie, J.Chem.Educ. 47, 18(1970)
  5. ↑ a b c d e f g h i j k l m n o p q r s t u v w x y z aa ab ac ad ae Petrucci, R. H.; W. S., Harwood; F. G., Herring (2002). 普通化學：原理與現代應用 (第 8 版). Prentice-Hall. ISBN 978-0-13-014329-7.
  6. ↑ a b c d e f g h i j k l m n Miessler, G. L.; Tarr, D. A. (1999). 無機化學 (第 2 版). Prentice-Hall. pp. 54–62. ISBN 978-0-13-841891-5.
  7. ↑ Miessler, G. L.; Tarr, D. A. (1999). 無機化學 (第 2 版). Prentice-Hall. p. 55. ISBN 978-0-13-841891-5.
  8. ↑ Petrucci, R. H.; W. S., Harwood; F. G., Herring (2002). 普通化學：原理與現代應用 (第 8 版). Prentice-Hall. pp. 413–414 (表 11.1). ISBN 978-0-13-014329-7.
  9. ↑ a b c d e f g h i j k l m n o p q r Housecroft, C. E.; Sharpe, A. G. (2005). 無機化學 (第 2 版). Pearson. ISBN 978-0-130-39913-7.
  10. ↑ a b Baran, E. (2000). "五角錐形 XeOF5- 和 IOF2−5 陰離子的平均振動幅度". J. Fluorine Chem. 101: 61–63. doi:10.1016/S0022-1139(99)00194-3.
  11. ↑ Anderson, O. P. (1983). "書評：無機立體化學（作者：David L. Kepert）" (PDF). Acta Crystallographica B. 39: 527–528. doi:10.1107/S0108768183002864. Retrieved 14 September 2020. 基於對電子對排斥的常見觀點的系統定量應用
  12. ↑ Brittin, W. E. (1945). "四面體碳原子的價鍵角". J. Chem. Educ. 22 (3): 145. Bibcode:1945JChEd..22..145B. doi:10.1021/ed022p145.↑ "四面體兩條邊的夾角" Template:Webarchive – Maze5.net
  13. ↑ a b c d Wiberg, E.; Holleman, A. F. (2001). 無機化學. Academic Press. ISBN 978-0-12-352651-9.
  14. ↑ Power, Philip P. (2003 年 9 月). "乙炔的矽、鍺、錫和鉛類似物". Chem. Commun. (17): 2091–2101. doi:10.1039/B212224C. PMID 13678155.
  15. ↑ Nagase, Shigeru; Kobayashi, Kaoru; Takagi, Nozomi (2000 年 10 月 6 日). "重第 14 族元素之間的三鍵。理論方法". J. Organomet. Chem. 11 (1–2): 264–271. doi:10.1016/S0022-328X(00)00489-7.
  16. ↑ Sekiguchi, Akira; Kinjō, Rei; Ichinohe, Masaaki (2004 年 9 月). "含矽-矽三鍵的穩定化合物" (PDF). Science. 305 (5691): 1755–1757. Bibcode:2004Sci...305.1755S. doi:10.1126/science.1102209. PMID 15375262. S2CID 24416825. [失效連結]
  17. ↑ LiOLi 分子的鍵長光譜測定：強離子鍵，D. Bellert，W. H. Breckenridge，J. Chem. Phys. 114，2871 (2001)；doi:10.1063/1.1349424
  18. ↑ a b c d 分子幾何模型，Gillespie R. J.，Robinson E.A. Chem. Soc. Rev.，2005，34，396–407，doi: 10.1039/b405359c
  19. ↑ Wells A.F. (1984) 結構無機化學 第 5 版 牛津科學出版物 ISBN 0-19-855370-6
  20. ↑ Template:Housecroft2nd
  21. ↑ Peterson, W.; Holloway, H.; Coyle, A.; Williams, M. (1971 年 9 月). "氙周圍的反稜柱配位：硝醯八氟合氙(VI)的結構". Science. 173 (4003): 1238–1239. Bibcode:1971Sci...173.1238P. doi:10.1126/science.173.4003.1238. ISSN 0036-8075. PMID 17775218. {{cite journal}}: Cite has empty unknown parameter: |month= (help)
  22. ↑ Hanson, Robert M. (1995). 分子摺紙：精確比例模型，紙製. University Science Books. ISBN 0-935702-30-X.
  23. ↑ Kaupp, Martin (2001). ""非 VSEPR" 結構和 d0 系統中的鍵合". Angew. Chem. Int. Ed. Engl. 40 (1): 3534–3565. doi:10.1002/1521-3773(20011001)40:19<3534::AID-ANIE3534>3.0.CO;2-#.
  24. ↑ Gillespie, Ronald J.; Noury, Stéphane; Pilmé, Julien; Silvi, Bernard (2004). "對第 4 週期金屬 Ca 至 Mn 的 d0 分子幾何的電子局域化函式研究". Inorg. Chem. 43 (10): 3248–3256. doi:10.1021/ic0354015. PMID 15132634.
  25. ↑ Gillespie, R. J. (2008). "VSEPR 模型的五十年". Coord. Chem. Rev. 252 (12–14): 1315–1327. doi:10.1016/j.ccr.2007.07.007.
  26. ↑ Landis, C. R.; Cleveland, T.; Firman, T. K. (1995). "Making sense of the shapes of simple metal hydrides". J. Am. Chem. Soc. 117 (6): 1859–1860. doi:10.1021/ja00111a036.
  27. ↑ Landis, C. R.; Cleveland, T.; Firman, T. K. (1996). "Structure of W(CH3)6". Science. 272 (5259): 179–183. doi:10.1126/science.272.5259.179f.
  28. ↑ King, R. Bruce (2000). "Atomic orbitals, symmetry, and coordination polyhedra". Coord. Chem. Rev. 197: 141–168. doi:10.1016/s0010-8545(99)00226-x.
  29. ↑ Haalan, A.; Hammel, A.; Rydpal, K.; Volden, H. V. (1990). "The coordination geometry of gaseous hexamethyltungsten is not octahedral". J. Am. Chem. Soc. 112 (11): 4547–4549. doi:10.1021/ja00167a065.
  30. ↑ Template:Greenwood&Earnshaw
  31. ↑ Seijo, Luis; Barandiarán, Zoila; Huzinaga, Sigeru (1991). "Ab initio model potential study of the equilibrium geometry of alkaline earth dihalides: MX2 (M=Mg, Ca, Sr, Ba; X=F, Cl, Br, I)" (PDF). J. Chem. Phys. 94 (5): 3762. Bibcode:1991JChPh..94.3762S. doi:10.1063/1.459748. hdl:10486/7315.
  32. ↑ Anslyn E.V. and Dougherty D.A., Modern Physical Organic Chemistry (University Science Books, 2006), p.57
Retrieved from "https://wikibook.tw/w/index.php?title=Inorganic_Chemistry/Chemical_Bonding/VSEPR_theory&oldid=4046776"
華夏公益教科書