無機化學導論/奈米材料基礎科學

  奈米材料基礎科學

            

彩色玻璃、防曬霜、磁性硬碟、非均相催化劑、消費電子產品、防汙服裝、自清潔玻璃和醫療診斷有什麼共同點？它們都從奈米材料中獲得了一些特殊的效能和用途：普通的元素和無機化合物，如金、銀、TiO₂、鉻、SiO₂和矽，當它們的特徵尺寸在1 到 100 奈米之間時，會獲得不同的效能。在本章中，我們將學習奈米材料的基礎科學，即是什麼讓它們的尺寸如此不同。

第 11 章的學習目標

• 瞭解奈米級半導體和磁性粒子中介觀行為的物理基礎。
• 描述箱中粒子方程如何應用於量子阱中的電子。
• 使用 Brus 公式計算奈米級半導體粒子的帶隙能量。
• 使用表面能概念計算奈米粒子的熔點和蒸氣壓變化。
• 描述用於製造尺寸均勻的半導體和金屬奈米晶體的 方法。
• 解釋金屬奈米粒子中局域表面等離子體共振效應的起源。
• 描述金屬奈米粒子新興的分析和生物醫學應用。

  11.1 物理和長度尺度：腔雷射器、庫侖阻塞、奈米磁體

奈米材料的特殊效能並非來自不同的物理定律，這些定律對於大小不同的物體都是相同的。例如，牛頓第二定律 (F = ma)、庫侖定律 (E = q₁q₂/4πε₀r) 以及能量守恆和動量守恆定律對於富勒烯 (C₆₀) 和標準足球都是一樣的。然而，電子的物理特性、原子和光子自然會產生特徵長度尺度，我們已經見過其中的一些。例如，在第 6 章中，我們發現良好金屬中電子的平均自由程約為 40 奈米。在第 10 章中，我們瞭解到摻雜 Si 中電子或空穴的玻爾半徑約為 4 奈米，以及半導體中庫珀對的相干長度在幾個奈米到 1 微米之間。當物體相對於這些特徵長度變小時，它們的物理特性會以有趣的方式發生變化。存在於相關長度尺度上的材料被稱為介觀（meso = "介於"，scopic = "大小"），這意味著它們從一種行為轉變為另一種行為——大型物體的整體行為。這種長度尺度對於不同型別的特性是不同的，但對於許多特性而言，它發生在 1 到 100 奈米之間。我們用幾個例子來說明這一點。

VCSEL 器件結構。這是一個底部發射多量子阱VCSEL。

腔雷射器。垂直腔面發射雷射器（或 VCSEL）是一種基於半導體的器件，它相對於晶片平面的方向垂直髮射光。這些器件正在開發和用於高功率應用，例如雷射手術、用於軍事監視的紅外照明以及雷射切割工具。VCSEL 的基本設計如右圖所示。VCSEL 本質上是一個發光二極體，包含 III-V 半導體 (Al,Ga)As 的 p 型和 n 型區域。但是，它具有兩個特殊特徵。首先，半導體的折射率在結點之上和之下被調製以形成布拉格反射鏡。這些反射鏡反射在結點中發射的光，因此光子密度在那裡變得非常高，這是受激發射和雷射的必要條件。布拉格反射鏡堆疊是不對稱的（底部更薄），因此光只能從一個方向從結點中逸出。其次，結點本身包含一層薄的“量子阱”層 (In,Ga)As，這是一種 III-V 半導體，其帶隙比周圍的 (Al,Ga)As 層小。

量子阱結構（其能帶圖如左圖所示）是雷射器的奈米級部分。 (Al,Ga)As 的導帶和價帶的能量包圍著薄的 (In,Ga)As 層的能量。因此，注入到該層中的電子和空穴無法逸出： (In,Ga)As 中的電子沒有足夠的能量“爬上”到 (Al,Ga)As 的導帶，而空穴無法“爬下”。限制在如此小阱中的電子錶現得像一個箱中粒子（正如我們在第 9 章關於電化物的背景下所瞭解的那樣）。
電子具有由以下方程定義的動能

$KE={\frac {h^{2}n^{2}}{8mL^{2}}}$

我們可以計算最低能級 (n=1) 和次低能級 (n=2) 之間的能量差，該能量差與 (In,Ga)As 層的厚度 (L) 的平方成反比。在這個計算中，我們需要使用 (In,Ga)As 中電子的有效質量，這大約是電子靜止質量的 7%。對於 8 奈米厚的層，這種能量是

$E={\frac {(2^{2}-1^{2})(6.626\cdot 10^{-34}Js)^{2}}{8\cdot 0.07\cdot (9.1\cdot 10^{-31}kg)(8\cdot 10^{-9}m)^{2}}}=4.0\cdot 10^{-20}J=0.25eV$

因此，VCSEL 腔將具有 0.25 eV 的共振能量，並在紅外光譜中以該能量發射光子 (λ ≈ 5000 nm)。請注意，由於腔能量與層厚度的平方成反比，因此基於這種設計的雷射器只能在奈米尺寸下工作。當腔的厚度增加三倍時，其共振能量將與室溫下的熱能相當 (kT = 0.026 eV)，雷射效應將被熱能“洗掉”。

面積為 A、介電層厚度為 d 的平行板電容器的基本設計

庫侖阻塞。電容器是一種（宏觀）裝置，用於儲存電荷。電容器的基本結構如右圖所示。當對這種裝置施加電壓時，它會在兩個板上產生與電壓成正比的電荷 (± Q)

$C={\frac {Q}{V}}$

電容 C 的大小由介電常數 ε 和介電層的尺寸 A 和 d 決定。

$C={\frac {\varepsilon A}{d}}$

我們還可以透過積分電壓乘以電荷來計算對電容器進行充電所做的功（即充電電容器儲存的能量）

單電子電晶體的示意圖。

$E=\int _{0}^{Q}V(q)\mathrm {d} q=\int _{0}^{Q}{\frac {q}{C}}\mathrm {d} q={1 \over 2}{Q^{2} \over C}={1 \over 2}CV^{2}={1 \over 2}VQ$

現在有趣的是，當我們使電容器變得非常小時，會發生什麼？這在一種名為單電子電晶體的裝置中尤為有趣，該裝置的示意圖如右圖所示。金屬柵極引線透過一層薄介電層與一個“量子點”隔開，該量子點可以是金屬或半導體粒子。這種金屬-介電-金屬夾層結構充當電容器，根據上面的方程式，用一個電子 (Q = e) 對其充電所需的能量是

$E={\frac {e^{2}}{2C}}$

其中 e 是電子的電荷，1.602 x 10^-19 庫侖。如果柵極寬度和橫向尺寸非常小，例如自組裝庫侖阻塞器件中可以輕鬆實現的 2 奈米，那麼對於典型的絕緣介電材料，需要約 200 mV 的電壓才能用一個電子對量子點充電。同樣，這種效應是奈米尺度特有的，因為 10 倍更大的器件面積將使單電子充電電壓約為 20 mV，這小於熱能 kT (26 meV)。因此，對於大於約 5-6 奈米的器件，在室溫下，單個電子充電事件會被熱波動“洗掉”。

像這樣的奈米電容器如何充當電晶體，在電路中充當開關？這種效應來自於電子的相互排斥。量子點上的一個電子會排斥任何其他想要透過施加源極和漏極之間的微小電壓而被強加到它上的電子。因此，量子點的電導率在零電壓的柵極偏壓下非常低，或者在任何柵極偏壓（200、400、600 mV...）下，這些偏壓將整數個電子 (1、2、3、...) 放在量子點上。但在這些電壓的中間（例如，在 100、300、500 mV 下），量子點上有 n 個電子還是 n+1 個電子，能量是相同的。這意味著電子可以在不改變能量的情況下跳上跳下，即它們可以從源極到漏極穿過量子點。這種效應在柵極電壓的規則步長中使量子點的電導率出現峰值。實際上，柵極可以充當開關，就像傳統的場效應電晶體一樣。單電子電晶體被研究作為超靈敏的靜電計和單分子化學感測器，因為量子點靜電環境的微小變化會使器件開啟或關閉。

縱向 和 垂直記錄，兩種型別的硬碟驅動器寫入頭。

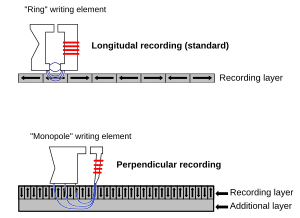
奈米磁體。鐵和氧化鉻等鐵磁性和亞鐵磁性材料用於硬碟驅動器中資訊的數字化儲存。單個儲存位可以垂直或平行於磁碟平面排列，如右圖所示，它們根據其磁偶極子的方向儲存邏輯“0”或“1”。為了有用，這種資訊必須是非易失性的，即磁位在沒有來自讀/寫頭的施加磁場的情況下必須保持其極化。

這種磁性儲存器的儲存密度令人印象深刻。一個 2.5 英寸的硬碟驅動器現在可以儲存 1 TB 的資訊，使用長度約為 0.5 µm 的棒狀磁性顆粒。我們現在有良好的合成方法，可以將這些相同的材料作為僅幾個奈米尺寸的晶體合成。為什麼不使用這些奈米晶體來製作密度更高的儲存磁碟呢？

包含超順磁性 Fe₃O₄ 奈米粒子的鐵磁流體，這些奈米粒子被油酸包裹並懸浮在油中，位於強永磁體的磁場中。

原因是翻轉磁化所需的能量（即，將“0”變成“1”，反之亦然）與尺寸密切相關。對於鐵磁體或亞鐵磁體，這種能量等於 Mr³，其中 M 是單位體積的磁能，r 是磁性顆粒的特徵尺寸（例如，立方體的邊長或球體的直徑）。對於典型的材料，如鐵，當 r 約為 3-5 奈米時，這種能量變得與 kT 相當。如此小的顆粒是 超順磁性 的，這意味著它們仍然具有很大的磁矩，因為它們的旋轉有序，但在沒有施加磁場的情況下，它們不會保留永久極化。因此，超順磁性顆粒不適合用作磁性記憶，但它們在其他方面很有趣且實用，例如在 鐵磁流體、磁共振成像 (MRI) 和一些新興的醫學診斷和治療應用中。

在這三個說明性的例子（涉及光發射、電子傳導和磁行為）中，向新屬性的轉變涉及一個交叉，其中系統的特徵能量與熱能 kT 相當。恰好，對於許多物理現象，這種交叉發生在奈米級的長度尺度上。

  11.2 半導體量子點

CdSe 奈米顆粒的原子解析度影像。

不同尺寸 CdSe 奈米顆粒的發射顏色。較小的顆粒發射藍光，因為激子能量隨著尺寸減小而增加。

最令人著迷和研究最充分的中觀效應之一發生在當一個或多個尺寸在幾奈米範圍內時，各種形狀的半導體顆粒中。這些所謂的“量子點”（0D）、“量子棒”（1D）和“奈米片”（2D）獲得了驚人的新電子和光學特性。

半導體量子點的合成將在下面更詳細地討論，其控制程度足以獲得幾千個原子的完美晶體，這在宏觀晶體中是統計上不可能的。右側顯示了這種晶體的影像。在合成過程中，這些晶體可以用外延配體的層或更寬頻隙半導體的殼（例如 CdSe 情況下的 ZnS）進行封端，使得內部核心有效地成為量子阱。由核心半導體激發形成的電子-空穴對被限制在那裡，無法到達顆粒的外表面，否則它們可能會在那裡被捕獲並在熱力學上覆合。因此，半導體量子點的帶隙發射量子產率通常很高，導致右側所示不同尺寸 CdSe 顆粒的明亮發射顏色。由於其強烈的窄發射帶，量子點作為生物成像應用的發光標籤以及太陽能電池和光學顯示器中的光吸收體和發射體而備受關注。半導體核-殼量子點的明亮光致發光是商業 量子點顯示器 的基礎，這種顯示器可以比有機發光二極體 (OLED) 顯示器製造出更大、更明亮的格式。

發射顏色的尺寸依賴性主要來自盒中粒子效應。當量子點吸收光時產生的電子和空穴被“盒”的限制束縛在一起，形成一個 激子。Louis Brus 使用一階微擾理論確定半導體量子點的帶隙近似為：

$E_{gap}=E_{gap,bulk}+{\frac {{h}^{2}}{8\mu {{R}^{2}}}}-{\frac {1.8{e}^{2}}{4R\pi \varepsilon {{\varepsilon }_{0}}}}+...$

其中 R 是粒子半徑，µ 是電子-空穴約化質量（1/µ = 1/m_e* + 1/m_h*），m_e* 和 m_h* 是電子和空穴的 有效質量，ε 是半導體的介電常數。在這個方程中，體帶隙後的第一項是由於激子限制引起的動能，第二項表示受限電子和空穴之間的靜電吸引能。由於能量是 R² 的函式，因此可以透過改變數子點的尺寸在可見光譜中進行廣泛調整。

  11.3 半導體奈米晶體的合成

用油酸、油醯基和羥基進行表面鈍化的 5 奈米直徑膠體硫化鉛奈米顆粒的完整原子模型。

早期關於半導體奈米顆粒中量子尺寸效應的研究使用了簡單的複分解反應來合成。例如，CdSe 和 PbS 可以透過以下反應在環境溫度下沉澱出來

CdCl₂(aq) + H₂Se(g) = CdSe (s) + 2 HCl(aq)

Pb(NO₃)₂ + H₂S(g) = PbS(s) + 2 HNO₃(aq)

透過在不同的基質中進行這些反應來限制顆粒的生長，例如在聚合物薄膜或沸石的矽酸鹽籠中，並且有時也使用封端配體來限制顆粒生長。雖然這些反應確實產生了奈米顆粒，但通常會獲得廣泛的顆粒尺寸分佈。這些顆粒也不穩定，容易發生 奧斯特瓦爾德熟化 - 其中較大的顆粒以較小的顆粒為代價生長以最大限度地減少總表面能 - 因為水性介質中形成酸的合成反應的可逆性。缺乏良好的樣品阻礙了詳細研究和半導體量子點應用的開發。

奈米粒子合成的重要進展出現在 1990 年代初期，當時 Murray、Norris 和 Bawendi 引入了第一個用於 II-VI 半導體量子點的非水、可控生長過程。 該合成的關鍵是 (1) 使用非水溶劑和封端配體來穩定產品，使其免受熟化，(2) 在高溫下進行反應以確保良好的結晶度，以及 (3) 將顆粒成核和生長步驟分開，從而獲得尺寸均勻的顆粒。以下說明了此過程

合成是在作為三辛基膦 (TOP) 和三辛基氧化膦 (TOPO) 混合物的配位性高沸點溶劑中進行的。在早期的實驗中，二乙基鎘等有機金屬鎘化合物用作金屬源，但後來發現這些劇毒和易燃化合物可以被 CdO 取代。在反應開始時，硒源，通常是二（三甲基矽基）硒，[(CH₃)₃Si]₂Se，溶解在 TOP 中，迅速注入熱的（350 °C）反應混合物中。該反應導致奈米粒子快速成核，但由於注入冷溶劑，溫度也會下降，因此成核事件很快結束。冷卻的溶液現在包含奈米晶體種子。它在 TOPO-Cd 和 TOP-Se 中過飽和，但顆粒生長緩慢進行，直到溶液再次加熱到生長溫度，約為 250 °C。顆粒生長和尺寸聚焦發生是因為較小的顆粒比較大的顆粒需要更少的新增材料才能生長 ΔR。這是因為圍繞球形種子的附加殼的體積為 4πR²ΔR，因此對於較大的 R，ΔR 較小。在高過飽和條件下可以獲得非常窄的粒子尺寸分佈，其中奈米粒子生長速度相對於粒子溶解和 奧斯特瓦爾德熟化 很快。 [6] 然後，可以透過向冷卻的反應混合物中新增非溶劑，例如己烷，進一步縮小尺寸分佈。最大的顆粒首先沉澱出來，然後是較小的顆粒。由於奈米顆粒被 TOP 的配體殼封端，因此在尺寸分離後，它們可以重新懸浮在有機溶劑中。

半導體量子點的**高溫合成**已被應用於多種材料，包括II-VI族、III-V族和IV-VI族半導體。透過這種方法的變體可以製備出**形狀可控**的單分散奈米顆粒。例如，可以透過調節條件使CdSe以閃鋅礦多晶型物形式成核，形成四面體形狀的種子，然後在每個三角形面上生長極性纖鋅礦“臂”，形成奈米晶體四足體。透過這種技術的變體可以製備出許多其他奈米晶體形狀，例如棒狀、箭頭狀、米粒狀（錐形棒狀）和極性結構，例如Janus棒。這些形狀控制策略通常涉及使用專門吸附在特定晶體面上並抑制其生長的配體。例如，己基膦酸配體選擇性地吸附在富Cd晶體面上，從而導致稜柱形纖鋅礦相CdSe奈米晶體的生長。

以金奈米粒子為催化劑，在氣-液-固（VLS）工藝中外延生長矽奈米線。

另一種廣泛使用的半導體奈米晶體合成方法涉及從分子前驅體和熔融金屬液滴中生長，如圖右側所示。**氣-液-固（VLS）**和相關的**溶液-液-固（SLS）**生長過程依賴於這樣一個事實，即矽、鍺、砷化鎵、磷化銦等半導體在高溫下可溶於金和銅等液態金屬。例如，四氯化矽（SiCl₄）在金奈米晶體表面的催化還原反應釋放出氯化氫氣體，並在金中形成矽的固溶體。矽的存在降低了金的熔點，隨著更多四氯化矽的反應，形成了矽-金合金的液態**共晶**液滴。當該液滴中矽的含量過飽和時，矽奈米晶體就會成核並生長。該反應可以在宏觀矽晶體的表面進行，在這種情況下，奈米晶體“晶須”從表面生長，通常為單晶，並且外延取向由基底的矽晶體面決定。晶須的直徑由金液滴的半徑控制，金液滴的半徑可以小到幾奈米，也可以大到幾微米。使用這種技術，可以生長出奈米線或微線的“森林”。由於奈米線的組成取決於供應到金液滴的前驅體，因此可以沿奈米線軸製備出具有不同組成的“圖騰柱”結構。還可以透過**化學氣相沉積（CVD）**在奈米線周圍生長半導體外殼。VLS工藝還可以透過使用雷射從固體靶材中燒蝕半導體來適應沒有分子前驅體的複雜成分。

透過這種方法制備的半導體奈米線是極其靈敏的**生物感測器**的基礎，在這種生物感測器中，奈米線上的任何分子結合事件都會強烈影響其電導率。 奈米線和微線陣列也被研究用作**太陽能電池**元件，並作為**鋰電池**材料被商業化生產，以及奈米級熱電、電子和光電器件。

  11.4 表面能

如圖右側所示，奈米粒子有很大一部分原子位於表面。 這種高表面積與體積比是許多奈米粒子物理性質的重要因素，例如它們的**熔點**和**蒸氣壓**，以及它們的**反應性**。例如，非均相催化劑通常基於奈米粒子，因為催化活性原子是位於粒子表面的原子。

**表面能始終為正值。**與所有表面化學相關的關鍵量是**表面能**。這是形成表面“懸空鍵”的（熱力學上不利的）能量。表面原子配位不足，由於斷裂鍵需要能量，因此表面原子總是比體相原子具有更高的能量。無論鍵合是共價鍵（如金屬）、離子鍵（如鹽）還是非共價鍵（如水等液體），都會發生這種情況。例如，我們在蠟表面上的水滴呈珠狀時看到了這種效應。水滴收縮成球形（抵消了使水滴變平的重力），以最大限度地減少表面懸空的氫鍵數量。

在金屬或半導體顆粒的情況下，表面會斷裂強共價鍵。例如，體相面心立方金中的金原子具有 12 個最近鄰，但晶體（111）表面（金最密集的晶體面）上的金原子在平面內具有 6 個最近鄰，在下方具有 3 個最近鄰，總共 9 個。我們可以預計該晶體面的表面能會略微降低（因為剩餘的鍵會變得稍微更強），約為體相金的 3/12 = **1/4 的鍵合能**，而這實際上是許多材料的相當好的經驗法則。當換算為每單位面積的能量時，金屬和無機鹽的表面能通常在 1-2 J/m² 範圍內。

**示例：** 體相金的昇華能為 334 kJ/mol，表面能為 1.5 J/m²。金晶體（111）表面上的原子損失了體相鍵能的百分比是多少？

要解決這個問題，我們需要知道每個金原子的表面積。金具有面心立方結構，晶胞邊長為 4.08 Å。由此我們可以確定 Au-Au 距離為 4.08/1.414 = 2.88 Å。在具有此原子間距的金原子六方排列中，每個原子的表面積為 (2.88 Å)² x 0.866 = 7.2 Ų。乘以阿伏加德羅常數，我們發現（111）晶體面上每摩爾金表面原子的面積為 **4.3 x 10⁴ m²。**

現在我們將此面積乘以表面能

(4.3 x 10⁴ m²/mol) x (1.5 J/mol) x (1 kJ/1000 J) = **+65 kJ** 每摩爾金表面原子。

65 kJ/334 kJ x 100% = **19%** 的體相鍵能被表面原子損失了。

從這個例子可以清楚地看出，奈米粒子的表面能會對其物理性質產生重大影響，因為奈米粒子中很大一部分原子位於表面。**熔點**急劇下降就是一個很好的例子。

固體奈米晶體通常是多面的，而透過熔化奈米晶體形成的液滴則採用球形形狀以最小化表面積。

為了最小化表面能，多面體固體奈米晶體熔化成球形液滴。

讓我們考慮熔化直徑為 2 nm 的銀奈米晶體，這意味著大約 1/2 的原子位於表面。球形液滴的表面積比多面體晶體低。例如，立方體的表面積是相同體積的球體的 1.24 倍。如果熔化時的表面積減少約 20%，並且表面能約為體相原子鍵合能的 1/4，那麼對於直徑為 2 nm 的奈米晶體，我們估計

ΔH°_熔化 ≈ ΔH°_{熔化，體相} - (1/2)(0.25)(1/4)ΔH°_汽化 = ΔH°_{熔化，體相} - 0.025 ΔH°_{汽化，體相}

其中 ΔH°_{汽化，體相}，即汽化熱，是體相晶體中原子的總鍵能。對於銀，ΔH°_{熔化，體相} = 11.3 kJ/mol 且 ΔH°_{汽化，體相} = 250 kJ/mol。由此我們可以計算出直徑為 2 nm 的 Ag 奈米晶體的熔化熱

ΔH°_熔化 ≈ 11.3 - (0.025)(250) = 5.1 kJ/mol

體相銀的熔點為 962 °C = 1235 K。假設熔化熵在體相和奈米晶體中相同，則奈米晶體的熔點應為 1235 K x (5.1/11.3) = 557 K = 284 °C，與體相值相比下降了近 700 度。實驗表明，直徑為 2 nm 的銀奈米晶體的熔點下降了約 **800 度**，降至 127 °C。 這是一個巨大的熔點變化，與我們的粗略估計大體一致。

相同的效應——表面原子相對於體相原子的能量不穩定——導致奈米晶體相對於相同材料的微晶體（或更大晶體）具有**較低的沸點**、**較高的蒸氣壓**、**較高的溶解度**和**較高的反應性**。

  11.5 奈米級金屬粒子

金奈米粒子中的五重孿晶

在過去的 20 年裡，奈米級金屬粒子一直是研究的熱點，尤其是它們獨特的**光學**、**磁性**和**催化**特性。各種形狀的金屬奈米晶體的合成變得越來越複雜和合理，就像上面描述的半導體奈米晶體的合成一樣。透過控制成核和生長的各個階段，並使用在生長過程中封端特定晶體面的配體，可以製備出各種有趣且有用的形狀的尺寸均勻的金屬奈米晶體，包括立方體、截角立方體、八面體、三角稜柱和高長徑比棒狀。透過利用將一種金屬替換為另一種金屬的置換反應，可以從其他形狀開始製備出複雜的空心形狀，例如奈米籠（如左側所示）。在這種情況下，固體銀奈米立方體被轉化為金奈米籠。

利庫爾格斯杯（公元四世紀的羅馬玻璃製品）獨特的顏色來自於貴金屬奈米顆粒。在透射光下，杯子呈現紅色，而在散射（反射）光下呈現綠色。

奈米晶體金、銀、銅和其他一些金屬的有趣的光學特性，源於它們價電子的集體振盪，這種現象被稱為等離子體共振。請記住，在這些金屬中，電子平均自由程很長（大約是原子大小的 100 倍），因此價電子在晶體中快速移動時，只感受到原子核的平均正電荷。照射到金屬上的光表現為振盪電場，以光的波長特徵頻率推拉價電子。這種情況非常類似於擺錘或彈簧上的重物。電子被推離平衡位置，會感受到一個與其位移成正比的恢復力。它們的運動可以用胡克定律來描述

F = kx

其中彈簧常數 k 決定了彈簧的“剛度”。在等離子體共振的情況下，k 與價電子數密度 n 和電子電荷 e 的平方成正比

k = ne²/ε₀

等離子體振盪的共振頻率由下式給出

ω_p = (k/m)^1/2 = (ne²/m_eε₀)^1/2

其中 m_e 是電子質量。對於大多數金屬，等離子體共振位於光譜的紫外部分，但對於一些金屬如金、銀和銅，它位於可見光部分。

等離子體金奈米顆粒的顏色取決於它們的大小和形狀。

對於遠小於光波長的金屬顆粒，這種效應被稱為局域表面等離子體共振，或 LSPR。LSPR 效應有三個重要結果

• 入射光波的區域性電場在顆粒表面顯著增強。這導致光學過程（如拉曼散射和熒光）產生巨大的增強因子。因此，某些分析光譜技術透過 LSPR 顯著增強。
• 在等離子體共振頻率附近，金屬奈米晶體強烈地吸收和散射光。這使得它們具有明亮的反射性，強烈的光吸收可用於光誘導的區域性加熱。這些性質正在應用於醫療診斷和治療，例如用於檢測和光熱破壞癌細胞。透過調整金奈米顆粒的大小和形狀，這些奈米顆粒在生物介質中比銀和銅更穩定，等離子體頻率可以調諧到組織透明的近紅外區域（700 到 900 奈米）。少量等離子體銀和金顆粒也能形成顏色鮮豔且散射性強的顏料，例如上圖右側所示的彩色玻璃。
• 等離子體頻率對顆粒周圍介質的折射率（即其化學環境）敏感。這使得金屬奈米顆粒在感測和生物感測應用中具有特殊意義。

金屬奈米顆粒散射和吸收光的理論。金屬奈米顆粒中的價電子在光波的電場中振盪。雖然這些振盪的本質在非球形金屬顆粒中比較複雜，但球形顆粒的理論相對簡單，事實上，它在一百多年前就被德國物理學家古斯塔夫·米推匯出來。

米考慮了一個球形顆粒與均勻電場 E 的相互作用，該電場以角頻率 ω（= 2πf）振盪。當顆粒直徑遠小於光波長時，這是一個很好的近似，如左側所示。該顆粒嵌入均勻的絕緣材料（例如溶劑）中，該材料具有介電常數 ε_diel。對於絕緣體，ε_diel 是一個正實數。

金屬的介電常數 ε 實際上是一個複數

$\epsilon =\epsilon '+i\epsilon ''$

這裡，實部 ε' 與光的折射有關，虛部 ε'' 與光的吸收有關。ε' 和 ε'' 都依賴於光的頻率。對於等離子體共振頻率附近的金屬，ε' 通常是一個負數。

光波被顆粒吸收的截面是

${\sigma _{absorption}}={\frac {9\omega }{c}}\epsilon _{diel}^{3/2}V{\frac {\epsilon _{metal}''}{(\epsilon _{metal}'+2\epsilon _{diel})^{2}+(\epsilon _{metal}'')^{2}}}$

光波被顆粒散射的截面是

${\sigma _{scattering}}={\frac {3}{2\pi }}({\frac {\omega ^{4}}{c}})\epsilon _{diel}^{2}V^{2}{\frac {(\epsilon _{metal}'-\epsilon _{diel})^{2}+(\epsilon _{metal}'')^{2}}{(\epsilon _{metal}'+2\epsilon _{diel})^{2}+(\epsilon _{metal}'')^{2}}}$

這兩個的總和是消光截面

${\sigma _{extinction}}={\sigma _{absorption}}+{\sigma _{scattering}}$

當分母中的 (ε'_metal + 2ε_diel) 項變小時，這些截面會變大。這種情況發生在

$\epsilon _{metal}'\simeq -2\epsilon _{diel}$

對於水中直徑為 15 奈米的金奈米顆粒，這種情況發生在大約 580 奈米處，導致膠體金溶液呈現出特徵性的酒紅色。改變溶液環境（例如，透過吸附分子到金表面）會改變ε_diel，從而略微改變顏色。

需要注意的是，散射的截面與顆粒的體積平方（V²）成正比，而吸收與 V 成正比。這意味著非常小的金顆粒（< 5 奈米）具有很強的吸收性，但散射性不強。較大的顆粒（>30 奈米）散射光非常強。因此，根據應用的不同，我們選擇較大和較小的顆粒。

貴金屬奈米顆粒的一個關鍵互補特性是它們可以很容易地與聚合物或小分子共價偶聯，這對於它們在生物醫學中的應用非常重要，通常透過其表面的硫醇或胺鍵。這賦予顆粒生物識別特性，使其能夠與特定的生物分子靶標結合。左側的圖說明了透過表面功能化可以賦予奈米顆粒的一些功能。

金奈米顆粒的聚集（在本例中透過向膠體溶液中新增鹽）導致顏色從酒紅色（左）變為藍色（右）。照片來源：威斯康星州立大學比洛伊特分校的喬治·利辛斯基

用硫醇封端的單鏈 DNA 對金奈米顆粒進行功能化是第一個奈米顆粒感測器的基礎，該感測器由西北大學的米爾金小組開發。DNA 包覆的奈米顆粒具有球形奈米金的特徵性酒紅色等離子體顏色。然而，當這些顆粒透過互補 DNA 鏈連線在一起時，共振頻率會發生偏移，導致藍色。這種顏色變化如右側圖所示，為目標 DNA 序列的存在提供了一個“試紙”。 DNA 的“熔化”——將其加熱到雙鏈 DNA 解離形成單鏈的溫度——會逆轉顏色變化。由於許多金顆粒的聚集，DNA 雜交/熔化轉變具有高度的協同性，因此轉變溫度非常尖銳。透過適當的溫度控制，顏色變化可以對這種方法檢測到的目標 DNA 中的單個鹼基錯配敏感。

基於奈米耀斑檢測的通用示意圖。

隨後的研究已經開發出針對這些球形核酸顆粒的複雜診斷和治療（“治療診斷”）應用。這些顆粒很容易穿透細胞膜，並可以報告活細胞內部發生的化學反應。

金奈米顆粒在這些應用中的一個重要特性是它們能夠猝滅其表面附近報告分子發出的熒光。含有髮夾環的核酸鏈可以將熒光分子定位在金表面附近，在那裡它們的熒光會被奈米顆粒猝滅。這些序列與目標 RNA 或 DNA 的雜交會導致熒光分子遠離奈米顆粒表面，從而使熒光重新開啟。因此，這些所謂的“奈米耀斑”可以發出特定基因在細胞內上調或下調的訊號。奈米耀斑是維爾金系統（由 Nanosphere，Inc. 開發並商業化）的基礎，用於檢測傳染病和癌症的標誌物。

  11.6 奈米材料的應用

本節的 PowerPoint 幻燈片

  11.7 討論問題

• 解釋分離成核和生長步驟是如何導致尺寸均勻的奈米顆粒的。
• Delia Milliron 及其同事最近發表的一篇論文（Nature，2013，500，323–326，doi:10.1038/nature12398）描述了能夠控制窗戶紅外透明度的等離子體氧化銦錫（ITO）奈米顆粒。解釋奈米顆粒的等離子體共振波長如何可以透過電化學摻雜來調節，以及這項發明如何可以節省用於加熱和冷卻建築物的一些能源。

  11.8 問題

1. 考慮一個包含 500 個原子的球形金奈米顆粒。如果一個原子的直徑大約為 3 Å，那麼顆粒中位於表面的金原子所佔比例是多少？

2. 現在考慮包含 500 個原子的汞小液滴。汞原子直徑也約為 3 Å。塊狀汞的汽化熱為 64.0 kJ/mol，汞的蒸氣壓為 0.00185 託 = 2.43 x 10^-6 atm。汞的表面張力（γ_Hg）為 0.518 N/m，表面過剩能量可以計算為 γ_HgA，其中 A 為表面積。利用這些資訊和克勞修斯-克拉佩龍方程（P = const•exp(-ΔH_vap/RT)），計算這些汞小液滴的蒸氣壓。

3. James Heath 及其同事（Phys. Rev. Lett. 1995, 75, 3466）在室溫下觀察到金奈米顆粒薄膜中的奧斯特瓦爾德熟化現象。從不均勻的粒徑分佈開始，他們發現大顆粒以犧牲小顆粒為代價而生長。根據你對問題 (1) 和 (2) 的答案，你能解釋這種現象嗎？

4. 塊狀鍺的帶隙為 0.67 eV。你預計直徑為 4 奈米的鍺奈米晶體會有多少帶隙？使用布魯斯公式，

$\Delta {{E}_{gap}}\approx {\frac {{h}^{2}}{8\mu {{R}^{2}}}}-{\frac {1.8{e}^{2}}{4R\pi \varepsilon {{\varepsilon }_{0}}}}+...$

其中 R 為粒子半徑，ε_Ge = 16.2，h = 6.6 10^-34 J s，1 eV = 1.6 10^-19 J，1 J = 1 kg m²/s²。以及 e²/4πε₀ = 1.44 10^-9 eV m。假設電子-空穴約化質量 μ 約為自由電子質量的 40%，m_e = 9.1 10^-31 kg。

5. 希臘配方（一種染髮產品）直到最近還含有醋酸鉛，醋酸鉛與頭髮中的半胱氨酸反應生成 PbS。塊狀 PbS 是一種帶隙為 0.3 eV（1 eV = 1240 奈米）的半導體。這些顆粒最初非常小，但隨著更多希臘配方被使用並與半胱氨酸反應，它們會逐漸長大。隨著顆粒的生長，它們的顏色會從無色逐漸變為黃色，最後變為黑色。解釋為什麼這些顆粒最初是無色的以及為什麼它們的顏色會發生變化。（希臘配方現在使用 Bi，Bi 的毒性低於 Pb，並且透過相同的機制起作用）