無機化學導論/離子型和共價型固體 - 能量學

第 9 章：離子型和共價型固體 - 能量學

在常壓下，只有三種鹼金屬鹵化物，CsCl、CsBr 和 CsI，採用 CsCl 結構。然而，在高壓下，其他鹼金屬鹵化物由於 CsCl 的 Madelung 常數較高，會從 NaCl 結構轉變為 CsCl 結構。

在第 8 章中，我們學習了關於離子化合物的晶體結構。一個很好的問題是，是什麼讓化合物選擇特定的結構？在解決這個問題時，我們將瞭解保持晶體結合在一起的力以及不同結構的相對能量。這將反過來幫助我們更定量地理解我們在前面章節中學習到的某些啟發式概念，例如硬軟酸鹼理論。

第 9 章的學習目標

• 瞭解半徑比規則的幾何基礎。
• 瞭解結構圖的化學基礎，以及為什麼它們比半徑比更能預測晶體結構。
• 使用 Born-Mayer 和 Kapustinskii 方程計算已知和假想化合物的晶格能。
• 使用晶格能構建 Born-Haber 迴圈，並計算迴圈中未知量。
• 使用晶格能預測低高氧化態的穩定性。
• 瞭解金屬額外 "共振" 穩定性的量子力學起源。
• 使用晶格能預測無機化合物溶解度和熱穩定性的趨勢。

9.1 離子半徑和半徑比

晶體中的原子透過靜電力、範德華力以及共價鍵結合在一起。因此，可以最大化這些吸引性相互作用強度的原子排列應該是最有利的，並導致最常見的觀察到的晶體結構。

原子半徑和離子半徑。請注意，陽離子總是比同一元素的中性原子（粉紅色）小，而陰離子更大。從元素週期表的任何一行從左到右，由於核電荷增加，中性原子和陽離子的尺寸都會縮小。（點選檢視更大的影像）

半徑比規則。早期的晶體學家在使用 X 射線衍射來解決無機固體的結構時遇到了麻煩，因為分析資料的某些數學工具尚未開發出來。一旦提出一個試探性結構，計算衍射圖譜相對容易，但如果先驗地對晶胞中原子的排列一無所知，則從衍射圖譜推斷出結構就很難了（而且至今仍然如此）。因此，開發一些關於猜測晶體中原子配位數和鍵合幾何的準則至關重要（並且仍然至關重要）。第一個此類規則是由萊納斯·鮑林提出的，他考慮瞭如何將不同半徑的帶相反電荷的球體堆積在一起。鮑林根據幾何考慮，提出“匹配”的質量取決於陰離子和陽離子的半徑比。

臨界半徑比。該圖用於配位數 6：平面上的 4 個陰離子顯示出來，1 個在平面上方，1 個在平面下方。穩定性極限在 r_C/r_A = 0.414 處

半徑比規則的基本思想如右圖所示。我們認為陰離子是晶體中的堆積原子，而較小的陽離子填充間隙位置（“孔”）。陽離子將在可以接觸到最多數量的陰離子的排列中找到位置。如果陽離子可以接觸到所有最近的鄰近陰離子，如右圖所示，對於與較大陰離子接觸的小陽離子來說，那麼匹配就很好。如果陽離子對於某個特定位置來說太小，那麼該配位數將不穩定，並且它會更傾向於選擇較低的配位結構。下表給出了對於特定配位幾何形狀給出最佳匹配的陽離子/陰離子半徑比的範圍。

配位數	幾何形狀	ρ = r陽離子/r陰離子
2	線性	0 - 0.155
3	三角形	0.155 - 0.225
4	四面體	0.225 - 0.414
4	平面正方形	0.414 - 0.732
6	八面體	0.414 - 0.732
8	立方體	0.732 - 1.0
12	立方八面體	1.0

不幸的是，使用這種思想來預測晶體結構存在幾個挑戰

• 我們不知道單個離子的半徑
• 晶體中的原子並不真正是離子 - 存在不同程度的共價性，具體取決於電負性差異
• 鍵長（因此離子半徑）取決於鍵強度和配位數（記住鮑林規則 D(n) = D(1) - 0.6 log n）
• 離子半徑取決於氧化態（電荷越高 => 陽離子尺寸越小，陰離子尺寸越大）

我們可以透過假設鍵長是半徑的總和（r₊ + r_-）來構建離子半徑表，如果離子在晶體中接觸的話。例如，考慮化合物 MgX 和 MnX，其中 X = O、S、Se。所有這些化合物都在 NaCl 結構中結晶

                      鍵長 (r_MX)

MgO  2.10      MgS  2.60      MgSe  2.73 Å

MnO  2.24      MnS  2.59      MnSe  2.73 Å

對於兩個較大的陰離子（S^2- 和 Se^2-），兩種陽離子的晶胞尺寸相同。這表明陰離子在這些結構中接觸。從幾何考慮，在這種情況下，陰離子半徑由下式給出

$r_{-}={\frac {r_{MX}}{\sqrt {2}}}$

因此，S^2- 和 Se^2- 離子的半徑分別為 1.84 和 1.93 Å。一旦確定了這些陰離子的尺寸，我們就可以從許多 MX 化合物的晶格常數獲得一組自洽的陽離子和陰離子半徑。

該模型效果如何？讓我們考慮四價金屬氧化物 (MO₂) 的結構，使用鮑林半徑和半徑比模型的預測

氧化物 MO2	半徑比	預測的配位數	觀察到的配位數（結構）
CO2	~0.1	2	2（線性分子）
SiO2	0.32	4	4（各種四面體結構）
GeO2	0.43	4	4（類似二氧化矽的結構）
"	0.54	6	6（金紅石）
TiO2	0.59	6	6（金紅石）
ZrO2	0.68	6	7（板鈦礦）
"	0.77	8	8（螢石）
ThO2	0.95	8	8（螢石）

請注意，陽離子的半徑取決於它們的配位數，因此對於配位數為 4 和 6 的 Ge⁴⁺ 以及對於配位數為 6 和 8 的 Zr⁴⁺ 計算出不同的半徑比。

對於這系列氧化物，該模型似乎相當有效。在所有情況下，都預測了正確的配位數，並且像 GeO₂ 和 ZrO₂ 這樣的臨界情況在具有不同配位數的結構中被發現。該模型還正確預測了 BeF₂（SiO₂ 型）、MgF₂（金紅石）和 CaF₂（螢石）的結構。

那麼鹼鹵化物 NaCl、KBr、LiI、CsF 等呢？除了 CsCl、CsBr 和 CsI 具有 CsCl (8-8) 結構外，它們都具有 NaCl 結構。在這種情況下，半徑比模型失效得很厲害。預測 Li⁺ 鹽 LiBr 和 LiI 具有四面體結構，而 KF 預測具有與 CsCl 相似的 8-8 結構。我們可以嘗試調整半徑（例如，使陽離子更大，陰離子更小），但我們對鹼鹵化物所能做到的最好的結果是正確預測大約一半的結構。由於鹼鹵化物顯然是離子化合物，這種失敗表明半徑比模型存在很大問題，它在 MO₂ 化合物中的成功是偶然的。

橄欖石的結構。M (Mg 或 Fe) = 藍色球體，Si = 粉色四面體，O = 紅色球體。

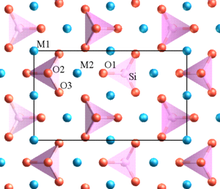
除了半徑比規則外，萊納斯·鮑林 還發展了其他有用的規則，這些規則有助於合理化並預測無機化合物的結構。鮑林規則 指出

• 穩定的結構是區域性電中性的。例如，在雙鈣鈦礦 Sr₂FeMoO₆ 的結構中，MO₆ (M = Fe²⁺, Mo⁶⁺) 八面體共享它們的所有頂點，而 Sr²⁺ 離子填充由八個 MO₆ 八面體包圍的立方八面體空腔。 為了實現區域性電中性，每個 O^2- 離子與一個 Fe²⁺ 和一個 Mo⁶⁺ 離子配位，因此 FeO₆ 和 MoO₆ 八面體在結構中交替出現。

• 陽離子-陽離子排斥應最小化。陰離子多面體可以共享頂點（如鈣鈦礦結構中）而沒有任何能量損失。共享多面體邊，特別是共享面，會導致陽離子-陽離子排斥，應該避免。例如，在金紅石中，TiO₂ 的最穩定多形體，TiO₆ 八面體共享頂點和兩個相對邊，在結構中形成帶。在銳鈦礦 TiO₂ 中，每個八面體共享四個邊，因此銳鈦礦多形體在熱力學上不太穩定。

• 高電荷陽離子在陰離子多面體中往往不共享邊甚至頂點，尤其是在配位數較低的情況下。例如，在正矽酸鹽（如橄欖石 (M₂SiO₄)）中，存在孤立的 SiO₄^4- 四面體。

正如我們很快將看到的那樣，所有鮑林規則都可以在晶格能考慮的基礎上得到證明。在離子化合物中，使陰離子-陽離子相互作用最大化，同時使陽離子-陽離子和陰離子-陰離子接觸最小化的原子排列在能量上是最優的。

  9.2 結構圖

結構圖將結構與電負性等性質繪製在一起，在正確預測配位數和晶體結構方面比半徑比規則更一致。這種方法的早期例子之一是由 Mooser 和 Pearson 在 1959 年發表的。

Mooser-Pearson 圖根據原子的平均主量子數及其電負性差異來對映晶體結構。這種圖背後的基本思想是

• 電負性差異越大，化合物越離子化。較高的離子性會導致較高的配位數，因為陰離子喜歡包圍陽離子（反之亦然）。
• 較高的主量子數會導致更少的 s-p 雜化，更少的定向鍵合，因此配位數更高。我們之前在 IV 族元素的結構中看到了這種趨勢：隨著組的下降，配位數從 3-4 (碳) 逐漸增加到 12 (鉛)。

Mooser-Pearson 圖中的線將具有 CsCl、NaCl 和四面體（纖鋅礦和閃鋅礦）結構的 MX 化合物分開。請注意，在圖中，纖鋅礦的離子性高於閃鋅礦，這與我們在第 8 章中討論的“船”和“椅”環結構一致。二態性化合物往往落在邊界上。總的來說，Mooser-Pearson 圖在預測結構方面比半徑比規則犯的錯誤要少得多。對於 MX₂ 結構也有類似的圖，其中離子性的順序為 CaF₂ (8:4 配位) > 金紅石 (6:3) > 二氧化矽結構 (4:2)。

  9.3 晶體固體的能量學：離子模型

NaCl 晶體結構是計算晶格能和從 Born-Haber 迴圈計算生成焓的原型。

許多離子化合物具有簡單的結構。由於使原子結合在一起的力主要是靜電的，我們可以用良好的精度計算晶格的內聚能。關於這些晶格能計算，有趣的問題是

• 晶格能計算的精度如何？
• 它們告訴我們關於離子晶體中化學鍵的什麼資訊？
• 我們可以使用晶格能來預測溶解度、穩定性和反應性等性質嗎？
• 我們可以使用晶格能來預測離子化合物的晶體結構嗎？

讓我們首先看看使離子晶格結合在一起的力。主要有兩種型別的力決定了離子鍵的能量。

1) 靜電力的吸引和排斥（庫侖定律）：兩個帶電荷為 z₊ 和 z_- 的離子，相隔距離為 r，受到力 F 的作用

$\mathbf {F} =-{\frac {e^{2}}{4\pi \epsilon _{0}}}{z_{+}z_{-} \over r^{2}}\qquad$

其中

e = 1.6022×10⁻¹⁹ C

4 π ε₀ = 1.112×10⁻¹⁰ C²/(J m)

對於異號離子，這種力是吸引力。

那麼靜電勢能 E_elec 由下式給出

$\mathbf {E} _{elec}=\int _{\infty }^{r}F(r)\,\mathrm {d} r={\frac {e^{2}}{4\pi \epsilon _{0}}}{z_{+}z_{-} \over r}.\qquad$

E_elec 的符號對於陽離子和陰離子之間的吸引相互作用為負。也就是說，相反帶電離子相互靠近的距離越近，勢能越低。

2) 閉殼排斥。當一個離子的閉合殼層中的電子與另一個離子的電子重疊時，會產生一種來自泡利不相容原理的排斥力。第三個電子不能進入已經包含兩個電子的軌道。這種力是短程的，通常被模擬為隨著原子間距離 r 的指數衰減或高次方衰減。例如，在玻恩近似中，B 是一個常數，ρ 是一個具有長度單位的數，通常從壓縮性資料中經驗確定。ρ 的典型值為 0.345 Å。

$\mathbf {E} _{repulsion}=B\exp \left({\frac {-r}{\rho }}\right).\qquad$

兩個原子之間離子鍵的能量計算方法是，將淨靜電能和閉殼層排斥能結合起來，如圖所示。注意，目前我們忽略了離子之間的範德華吸引能，我們將在下面解釋。對於一對離子，離子之間的平衡距離由總能量曲線的最小值決定。在這個距離上，作用在每個離子上的淨力為零。

馬德隆常數是透過在擴充套件球體方法中對離子 0 與其他離子之間的靜電相互作用進行求和而計算得出的。每個數字代表求和的順序。例如，標記為 1 的離子表示六個最近鄰（吸引力相互作用），標記為 2 的離子是接下來的 12 個最近鄰（排斥力相互作用），等等。請注意，如果對殼層 1-2-3... 進行求和，則收斂速度非常慢，但有一些數學方法可以對它進行求和，從而得到快速收斂的級數。

晶格的靜電能。我們可以使用這些方程透過對所有離子對之間的相互作用進行求和來計算晶體的晶格能。由於閉殼層排斥力是短程力，因此通常只對相鄰離子之間的相互作用進行計算。然而，庫侖力是長程力，必須在整個晶體上進行計算。這個問題最早由德國物理學家 埃爾溫·馬德隆 在 1918 年解決。^[4]

考慮右圖中 NaCl 結構中標記為“O”的離子。我們可以看到，最近鄰相互作用 (+ -) 與標記為“1”的離子之間是有吸引力的，而下一個最近鄰相互作用 (- - 和 + +) 是排斥的，等等。在 NaCl 結構中，從晶胞中心的離子開始計數，有 6 個最近鄰（在立方體的面上），12 個下一個最近鄰（在立方體的邊上），8 個在下一個殼層中（在立方體的頂點上），等等。它們與離子“0”的距離逐漸增加：r_o、√2 r_o、√3 r_o，等等，其中 r_o 是最近鄰距離。

現在我們可以將離子“O”的靜電能寫成

$\mathbf {E} _{elec}=-6{\frac {e^{2}}{4\pi \epsilon _{0}}}{z_{+}z_{-} \over r_{o}}+12{\frac {e^{2}}{4\pi \epsilon _{0}}}{\frac {z_{+}z_{-}}{{\sqrt {2}}r_{o}}}-8{\frac {e^{2}}{4\pi \epsilon _{0}}}{\frac {z_{+}z_{-}}{{\sqrt {3}}r_{o}}}+...$

將常數和最近鄰鍵長 r_o 因式分解，我們得到

$\mathbf {E} _{elec}={\frac {e^{2}}{4\pi \epsilon _{0}}}{z_{+}z_{-} \over r_{o}}\left(6-{\frac {12}{\sqrt {2}}}+{\frac {8}{\sqrt {3}}}-{\frac {6}{\sqrt {4}}}+\cdots \right)$

其中括號中的求和是無量綱的，它緩慢收斂到一個值為 A = 1.74756 的值。將此公式推廣到任何三維離子晶體，我們得到一個函式

$\mathbf {E} _{elec}={\frac {e^{2}}{4\pi \epsilon _{0}}}{z_{+}z_{-} \over r_{o}}NA\qquad$

其中 N 是阿伏伽德羅常數（因為我們計算的是每摩爾離子的能量），A 被稱為 馬德隆常數。馬德隆常數僅取決於離子的幾何排列，因此它在不同型別的晶體結構之間變化，但在給定的結構型別內它不會改變。因此，MgO 和 NaCl 具有相同的馬德隆常數，因為它們都具有 NaCl 結構。

下表列出了幾種常見結構的馬德隆常數。約化馬德隆常數是透過將值歸一化到化學式單元中的離子數量而得到的。從表中可以看出，不同結構的約化馬德隆常數非常相似。這使得很難根據靜電能計算來確定給定化合物最穩定的結構。有趣的是，約化馬德隆常數的趨勢大致遵循離子性的趨勢（參見第 9.2 節中的 Mooser-Pearson 圖）。例如，纖鋅礦的馬德隆常數略高於閃鋅礦，這與我們之前的結論一致，即纖鋅礦結構更受極性化合物的青睞。

結構	馬德隆常數，A	約化馬德隆常數，2A/n
NaCl（石鹽）	1.7476	1.7476
CsCl	1.7627	1.7627
ZnS（閃鋅礦）	1.6381	1.6381
ZnS（纖鋅礦）	1.6413	1.6413
CaF2（螢石）	2.5194	1.6796
TiO2（金紅石）	2.4080	1.6053
Al2O3（剛玉）	4.172	1.6688

氟化鋰（這裡顯示為燒杯中的一塊大的單晶體）是唯一一種不溶於水的鹼金屬鹵化物。LiF 的晶格能是所有鹼金屬氟化物中最負的，因為 Li⁺ 和 F^- 都是小離子，而 E_L 與 1/r₀ 成正比。

晶體的總晶格能。現在我們有了靜電能的公式，就可以加上閉殼層排斥項，得到一個可以給出總晶格能的方程。

$E_{L}={\frac {e^{2}}{4\pi \epsilon _{0}}}{\frac {z_{+}z_{-}}{r_{o}}}NA+NB\exp \left({\frac {-r}{\rho }}\right).\qquad$

在平衡鍵長處，所有離子的力都為零，我們可以利用這個事實來消除常數 *B*。

$\left[{\frac {dE}{dr}}\right]_{r=r_{o}}=0.\qquad$

由此，我們得到了Born-Mayer 方程。

$E_{L}={\frac {e^{2}}{4\pi \epsilon _{0}}}{\frac {z_{+}z_{-}}{r_{o}}}NA\left(1-{\frac {\rho }{r_{o}}}\right).$

這樣表達，*E_L* 是一個負數（因為 z₊ 和 z_- 符號相反）。它代表從無限遠處分離的一摩爾氣態離子形成一摩爾固態鹽的能量變化。

  9.4 NaCl 和鹵化銀的 Born-Haber 迴圈

現在我們有了離子晶體晶格能的方程式，我們可以問一個問題，它的準確性如何？記住，我們在推匯出這個公式時做了一些近似。我們假設晶格是完全離子性的，忽略了離子的範德華吸引能，並假設鍵閤中沒有共價貢獻。

讓我們考慮食鹽 (NaCl) 的晶格能。

Na⁺(g) + Cl^-(g) --> NaCl(s)

為了計算晶格能，我們將物理常數合併在一起。

$E_{L}(kJ/mol)=(1389.3){\frac {Az_{+}z_{-}}{r_{o}}}(1-{\frac {.345}{r_{o}}})$

其中 r_o 以 Å 為單位。現在我們可以使用 r_o = 2.814 Å 計算 NaCl 的晶格能，如

$E_{L}=-(1389.3){\frac {1.7476}{2.814}}(1-{\frac {.345}{2.814}})=-766.5$ kJ/mol

我們可以選擇性地構建一個**Born-Haber 迴圈**，用於從元素形成 NaCl 並計算晶格能作為迴圈中“缺失的”項。

NaCl 的 Born-Haber 迴圈

S= Na(s) 的昇華能

IP= Na(g) 的電離能

D= Cl₂(g) 的鍵解離能

EA= Cl(g) 的電子親和能

E_L= NaCl 的晶格能

R= 氣體常數

T= 絕對溫度

根據**蓋斯定律：** ΔH_f = S + 1/2D + IP + EA + E_L - 2RT = **-396 kJ/mol**

這裡我們必須減去 2RT 將我們的能量迴圈轉換為焓迴圈，因為我們在製造 NaCl(s) 時壓縮了 2 摩爾氣體，並且 PΔV = ΔnRT，其中 Δn = -2。

實驗測得的 NaCl 的 ΔH_f 為 **-411 kJ/mol**

由於迴圈中的所有其他數字都是準確已知的，因此我們計算中的誤差只有約 15 kJ（約為 E_L 的 2%）。這個結果很有希望，因為我們忽略了範德華項。

但是……我們如何才能忽略範德華項呢？

這是因為我們使用**能量最小化**來獲得 Born-Mayer 方程中的排斥能。如果我們低估了晶格的吸引能，能量最小化準則確保排斥能也被低估。這兩個誤差部分抵消，因此計算中的總體誤差很小。

我們可以透過明確包含離子之間的短程範德華吸引能來做得更好。下表顯示了更詳細的離子氟化物晶格能計算結果，其中明確包含了範德華項。在這種情況下，誤差僅為 E_L 的約 1%。

化合物	計算的晶格能 (kJ/mol)	Born-Haber 迴圈得到的實驗 EL
MgF2（金紅石結構）	-2,920	-2,908
CaF2（螢石結構）	-2,586	-2,611
BaF2（螢石結構）	-2,326	-2,368

鹵化銀

一滴硝酸銀溶液加入稀鹽酸溶液中，會立即形成白色氯化銀沉澱。此反應可用作溶液中鹵化物離子存在的定性測試。AgCl、AgBr 和 AgI 的晶格能中共價鍵合的貢獻使得這些鹽在水中微溶。

對具有 NaCl 結構（AgF、AgCl、AgBr）或閃鋅礦結構（AgI）的鹵化銀重複此練習很有趣。

鹵化銀	計算的	迴圈	差異 (kJ/mol)
AgF	-920	-954	34
AgCl	-833	-908	75
AgBr	-816	-900	84
AgI	-778	-883	105

從表中可以看出，AgF 的誤差很小，而對於較重的鹵化銀，誤差逐漸增大。然而，即使對於 AgI，我們仍然獲得了大約 12% 誤差內的答案。我們是否應該將與離子模型計算值的一致性解釋為這些化合物是離子性的？顯然，這種描述不適合 AgI，其中電負性差異 Δχ 僅為 0.6（將此值與 C-H 鍵的 0.4 相比較，我們通常將其視為非極性的）。

同樣，我們可以將計算值與實驗獲得的能量之間偶然的一致性解釋為補償誤差。我們的晶格能計算在較重的鹵化銀的情況下*高估了*離子貢獻，但在*低估了*共價貢獻。在這些化合物中，只有 AgF 可溶於水，應被認為是離子化合物。其他化合物在水中的溶解度逐漸降低（AgCl、AgBr 和 AgI 的 K_sp 分別為 10^-10、10^-13 和 10^-16），反映了隨著 Δχ 減小共價性增加。

這個故事的寓意是，基於離子模型的簡單晶格能計算效果很好，但*並不一定意味著這些化合物是離子性的*！

  9.5 Kapustinskii 方程

從上面的討論可以清楚地看出，如果已知離子晶體的結構，則可以相當準確地計算其晶格能 E_L。但是，如果我們不知道未知結構的新化合物或假設化合物的結構，我們如何計算 E_L 呢？回想一下，不同的晶體結構的約化馬德隆常數大致相同。俄羅斯化學家 A. F. Kapustinskii 認識到這一事實，並設計了一個公式，如果我們知道組成離子的單價半徑，則可以計算任何化合物的 E_L。

馬德隆常數 A 與化學式中離子的數量 (n) 成正比，因此將 A 除以 n 可以得到類似的值，如以下表格所示。

A/n ~ 不變

結構	A/n
NaCl	0.874
CsCl	0.882
金紅石	0.803
螢石	0.800

卡普斯廷斯基注意到，M⁺ 和 M²⁺（單價與二價半徑）之間離子半徑的差異在很大程度上彌補了單價（NaCl，CsCl）和二價（金紅石，CaF₂）結構之間 A/n 的差異。因此，他得到一個使用平均馬德隆常數的晶格能公式，並將其修正為單價半徑。在 卡普斯廷斯基公式 中，晶格能（kJ/mol）由以下公式給出。

$\mathbf {E} _{L}={1213.8z_{+}z_{-}n \over r_{+}+r_{-}}(1-{\frac {0.345}{r_{+}+r_{-}}})$

這裡，單價半徑之和用於代替 Born-Mayer 方程中的鍵長 r_o。這個公式的美妙之處在於它不需要任何關於化合物結構的知識。因此，它可以與 Born-Haber 迴圈相結合，來預測未知化合物的穩定性。正如我們將在下面看到的那樣，這在指導合成和預測無機固體的反應性方面是一個廣泛使用的工具。

  9.6 惰性氣體化合物的發現

二氟化氙 (XeF₂) 的晶體，透過光解 Xe 和 F₂ 的氣體混合物製得。XeF₂ 用作某些微電子製造工藝中 SiO₂ 的選擇性蝕刻劑。在 1962 年尼爾·巴特利特發現第一個氙化合物之前，人們認為 VIII 族元素（He，Ne，Ar，Kr，Xe）不能形成化學化合物。從那時起，化學家們發現了包含 Xe、Kr 或 Ar 的豐富惰性氣體化合物家族。

1962 年，在不列顛哥倫比亞大學，尼爾·巴特利特 研究強氧化劑 PtF₆，並且由於真空管線意外洩漏，他注意到該化合物與 O₂ 反應生成化學式為“PtF₆O₂”的固體。這個化學式表明 Pt 的氧化態為 +10，這顯然是不合理的，因為已知 PtF₆ 比分子氟 (F₂) 或分子氧 (O₂) 都是更強的氧化劑。巴特利特注意到該化合物的 X 射線粉末衍射圖譜與 Cs⁺AsF₆^- 的圖譜相似，Cs⁺AsF₆^- 是一種具有 CsCl 結構的鹽，其中八面體 AsF₆^- 離子佔據氯離子位置。這促使巴特利特提出了一種新的化合物 O₂⁺PtF₆^- 的配方。 後來的磁化率資料證實了順磁性 O₂⁺ 陽離子的存在，該陽離子（見第二章）的鍵級為 2.5。這種配方意味著 PtF₆ 是一種足夠強的氧化劑，可以氧化分子氧。

但是 PtF₆ 的氧化能力到底有多強呢？可以使用 Born-Haber 迴圈估算其電子親和力，並透過卡普斯廷斯基公式填入 O₂⁺PtF₆^- 的晶格能。



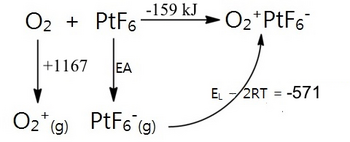
PtF₆ 的電子親和力 (EA) 可以計算為 EA = -159 - 1167 + 571 = -751 kJ/mol。為了說明這一點，這比原子氟的電子親和力 (334 kJ) 更放熱 417 kJ/mol。PtF₆ 是迄今為止製備的最強氧化劑！

巴特利特認識到 Xe 的電離能為 +1170 kJ，與 O₂ 的電離能非常接近。由於 Xe⁺ 的大小應該與 O₂⁺ 相似，因此在 O₂⁺PtF₆^- 結構的陽離子位置使用 Xe⁺ 時，晶格能應該大致相同。由於 Xe 與 PtF₆ 反應的 Born-Haber 迴圈中的所有其他項都是相同的，因此巴特利特得出結論，Xe⁺PtF₆^- 應該像 O₂⁺PtF₆^- 一樣是一種穩定的化合物。他買了一瓶氙氣，並將這兩種化合物反應，生成了橙色的固體。 雖然反應中最初形成的產物實際上可能是 Xe⁺PtF₆^-，但 Xe⁺ 自由基是一種強路易斯酸，會與過量的 PtF₆ 發生進一步反應。反應的最終產物被配製為 [XeF⁺][Pt₂F₁₁^-]，這是一種包含 Xe 的 +2 氧化態和 Pt 的 +5 氧化態的鹽。這一發現非常重要，因為它打破了八隅體規則推斷出的教條式觀念，即 VIII 族元素不能與其他元素形成鍵。該組的名稱從“惰性氣體”改為“惰性氣體”。隨後，合成了許多 Xe 的化合物以及一些 Kr 和 Ar 的化合物（Ar 難以氧化得多），並對其進行了表徵。

  9.7 高氧化態和低氧化態的穩定性

晶格能除了指導未知化合物的發現外，還有助於解釋不存在的化合物的缺失（即熱力學不穩定性）。 例如，CuF 和 AuF 是未知化合物，而 CuF₂、AuF₃ 和 AuF₅ 則是穩定的化合物。相反，AgF 是一種已知的穩定化合物。

從 CuF 的 Born Haber 迴圈來看，該化合物相對於元素來說應該是邊緣穩定的（ΔH_f^o = -140 kJ/mol）。那麼為什麼 CuF 未知呢？

為了深入瞭解這個問題，我們首先構建一個從元素形成 CuF₂ 的 Born-Haber 迴圈。該化合物相對於元素來說是穩定的，為 -368 kJ/mol。

將兩個迴圈組合起來，我們看到 CuF 的歧化成 Cu 和 CuF₂ 是自發的。從類似的迴圈中，我們還可以預測反應 3AuF → AuF₃ + 2Au 應該是自發的。

碘化亞銅 (CuI) 是一種在有機合成和人工降雨中使用的晶體化合物。這種化合物可以在實驗室中透過將可溶性 Cu²⁺ 鹽與碘化鈉或碘化鉀溶液反應制得。由於 CuI₂ 熱力學不穩定，反應釋放出 I₂，並形成 CuI 沉澱。

為什麼這些氟化物的最低氧化態不穩定？關鍵是 E_L 值的巨大差異（銅氟化物的情況下為 2908-972=1926 kJ）驅動了它們的歧化反應。請注意，當我們使用卡普斯廷斯基方程時，我們計算出 CuF₂ 的 E_L 大致是 CuF 的三倍。我們在兩個計算中使用相同的單價半徑，但 Cu 在 CuF₂ 中的電荷為 2+（使晶格能相對於 CuF 翻倍），並且包含 3/2 個離子。因此，CuF₂ 的乘積 z₊z_-n 是 CuF 的三倍。因此，E_L 值的差異將隨著單價鹽的 E_L 增加而增加。我們知道，氟化物由於陰離子半徑小，將比碘化物（陰離子半徑較大）具有更大的 E_L 值。因此，對於 CuF 來說，歧化反應比對於 CuI 來說更有利。

因此，較低氧化態與較高氧化態的穩定性取決於陰離子的尺寸。例如，在氟化物中，CuF 不穩定，但 CuF₂ 穩定。然而，在碘化物中，CuI 穩定，而 CuI₂ 不穩定。由此我們可以得出廣泛的結論：小的陰離子（O，F）傾向於穩定較高的氧化態，而大的陰離子（S，Br，I ...）傾向於穩定較低的氧化態。請注意，這種趨勢與陰離子的尺寸有關，而不是與陰離子的電負性有關。巧合的是，F 和 O 是電負性元素，但實際上是它們的小尺寸對晶格能及其對較高氧化態的穩定性有影響。

請記住，硬軟酸鹼規則可以用離子相互作用與共價相互作用的優勢來解釋。在這裡，我們將硬硬相互作用用（靜電）晶格能進行了量化。

Ag 似乎違背了週期性趨勢。為什麼 AgF 穩定？這是因為它的第二電離能非常高（2071 kJ 對比 Cu 的 1958 kJ，Au 的 1979 kJ）。因此，AgF 和 AgF₂ 都是已知的 Ag 氟化物。

  9.8 鹼金屬負離子化合物和電子負離子化合物

電子負離子化合物中的空穴和通道

晶格能的另一個有趣的結果是，涉及包含 Na^- 和 e^- 陰離子的某些鹽的形成。這些化合物分別被稱為鹼金屬負離子化合物和電子負離子化合物。 這些化合物中的大多數是由密歇根州立大學的詹姆斯·戴教授發現的。

鹼金屬在其價層中只有一個電子。例如，Na 和 K 的電子構型分別為 [Ar]3s¹ 和 [Kr]4s¹。雖然我們習慣於看到這些非常電正的元素在與電負性元素形成化合物時失去它們的電子，但它們也可以獲得一個電子以達到 [惰性氣體]ns² 構型。這在強電子給予體（如鹼金屬）中是可能的，尤其是當形成的陽離子透過與冠醚配位而得到穩定時。通常，這些化合物透過將鹼金屬和合適的冠醚在液氨中混合，然後蒸發氨來合成。

電化物鹽在類似條件下形成，只是在這種情況下，陰離子只是一個存在於晶體中陰離子“空腔”中的電子。晶體結構明顯類似鹽，陽離子（被冠醚或穴醚配體穩定的鹼金屬陽離子）在結構中與電子交替排列。

18-冠-6，一種與Na⁺ 陽離子強烈絡合的冠醚

用冠醚配體絡合Na⁺（K⁺，Rb⁺，Cs⁺）可穩定金屬的M⁺形式（“鹽”形式）。由於金屬陽離子和其配體殼層相當大，因此這些鹽的晶格能相當低。

電化物鹽的溶液是強還原劑，如它們在Birch 還原中的應用所示，其中芳香族化合物被氫化生成二烯烴。電化物也可用於將金屬離子還原成金屬。在無水氨中蒸發藍色電化物溶液會產生鈉的鏡面。隨著電子將氨還原成醯胺陰離子，這些溶液會慢慢失去顏色

[Na(NH₃)₆]⁺e⁻ + NH₃ → NaNH₂ + H₂

在晶格能和玻恩-哈伯迴圈的背景下，考慮一下如果不存在這些配體會發生什麼。也就是說，我們可以問一個問題，即鈉金屬是否更喜歡以金屬形式 Na(s) 存在，還是形成 sodide 鹽 Na⁺Na^-，或形成電化物鹽 Na⁺ e^-。當然，我們已經知道這個問題的答案。元素鈉顯然是一種金屬（它有光澤、導電，並具有體心立方晶體結構），從未在任何一種“鹽”形式中被觀察到。但這些形式在能量上相距多遠呢？

我們可以透過假設 Na- 離子的大小與 Br^- 相當，e^- 陰離子的大小與 Cl^- 相當來計算能量學。然後迴圈中的晶格能就與 NaBr 和 NaCl 的晶格能相同

這些計算得出的相當令人驚訝的結果是，鈉作為 sodide 鹽將是微弱穩定的，並且作為電化物將非常穩定（161 kJ）。這些簡單迴圈中的所有項都是精確已知的。但是我們在這裡一定做錯了什麼，因為 Na(s) 顯然是金屬。

這裡關鍵的、微妙的點是，玻恩-哈伯迴圈只考慮迴圈中物質的勢能（而不是總能量）。通常，我們可以忽略總能量中的動能部分，但在這種情況下，我們不能，因為存在共振的量子力學效應。

  9.9 金屬的共振能

鈉的金屬特性歸因於其離域價電子的共振穩定。

上述問題的解決方案必須考慮電子的量子力學性質。鈉金屬中的價電子處於遍佈整個晶體的離域軌道中。然而，在 Na⁺ e^- “鹽”形式中，電子被定位在特定的陰離子位點上。這種定位賦予了額外的動能（透過“盒子中的粒子”效應），從而增加了總能量。從盒子中一維粒子的量子力學結果中，我們得到

$KE={\frac {h^{2}n^{2}}{8mL^{2}}}$
其中

h = 普朗克常數 = 6.626 x 10^-34 J s

n = 能級，假設為最低能級，n = 1

m = 電子質量 = 9.109 x 10^-31 kg

L = 盒子的大小

如果我們將電子“盒子”的大小近似為 3 Å（3 x 10^-10 m），我們得到

$KE={\frac {(6.626\cdot 10^{-34})^{2}(6.022\cdot 10^{23})}{8\cdot (9.1\cdot 10^{-31})(3\cdot 10^{-10})^{2}}}=4.04\cdot 10^{5}J/mol=+404kJ/mol$

這種額外的動能使 Na⁺e^- “鹽”相對於電子離域金屬不穩定。

該計算並不十分準確，因為金屬中電子的動能不為零，並且因為“盒子”的大小沒有得到很好的定義。然而，它確實說明了電子離域對熱力學穩定金屬具有重大影響。這種情況與芳香族分子透過電子離域穩定完全類似。在苯等分子中，共振也是一種量子力學動能效應。一般來說，金屬中的共振穩定能明顯大於π-離域有機分子中的共振穩定能。例如，苯中六個π電子的共振能約為 151 kJ/mol，不到我們在鈉金屬中計算的（每個電子）值的一半。

Ca₂N 的晶體結構，藍色示意性地顯示了二維電子層。

有趣的是，幾種鹼金屬（和其他金屬元素）在超高壓下轉變為光學透明的絕緣相，其中價電子被定位。 這些高壓電化物相違背了一般規律（我們將在第 10 章中遇到），即絕緣體在足夠高的密度下會轉變為金屬。它們說明了元素的穩定結構如何取決於離子電化物結構的晶格能與電子離域金屬的共振能之間的權衡。

除了透過使鹼金屬與冠醚配體絡合而形成的類似鹽的電化物之外，最近還發現了一些固態氮化物和氧化物，例如 Ca₂N 和 Ca₂₄Al₂₈O₆₄，它們更準確地被表述為電化物，即 [Ca₂N⁺](e^-) 和 [Ca₂₄Al₂₈O₆₄]⁴⁺(e⁻)₄. 在這些化合物中，Ca、Al、O 和 N 原子具有其通常的八隅體氧化態（分別為 +2、+3、-2 和 -3），電子充當陰離子，填充晶體中籠狀空隙或層。例如，Ca₂N 採用反 CdCl₂ 結構，如右側所示，層間存在空隙，這些空隙被二維電子氣體佔據。與其他層狀材料一樣，Ca₂N 可以輕鬆地剝落成薄奈米片，同時保留其作為電化物的結構和特性。 這些化合物是強還原劑，並且還具有有趣的催化活性。

  9.10 鹼金屬氧化物的奇怪案例

鈉金屬在空氣中被氧化成過氧化鈉 Na₂O₂

K₂O（上）和Cs₂O（下）晶體結構的空間填充模型。氧原子為紅色，鉀離子為藍色，銫離子為品紅色。

意外的化學計量。鹼金屬氧化物，由鹼金屬（Li、Na、K、Rb、Cs）與氧氣反應制得，呈現出一種不尋常的趨勢。當鋰與氧氣反應時，我們得到二元氧化物Li₂O，這與第一族元素與第六族元素的結合預期一致。奇怪的是，鈉金屬氧化時最容易形成的氧化物不是Na₂O，而是過氧化物Na₂O₂，我們可以將其表示為(Na⁺)₂(O₂^2-)。對於鉀、銣和銫，我們得到超氧化物MO₂，其中含有超氧化物自由基陰離子(O₂^-.)，應該表示為(M⁺)(O₂^-)。雖然可以透過適當的金屬硝酸鹽(MNO₃)與元素鹼金屬M反應來製備Na₂O、K₂O、Rb₂O和Cs₂O， 但奇怪的是，這些“正常價”化合物不會透過金屬與氧氣的直接反應而形成。

由於鹼金屬都具有很強的電正性（χ = 0.8-1.0），而氧氣具有很強的電負性（χ = 3.5），因此我們預計所有透過將它們組合而成的化合物都是可靠的離子化合物。與這種圖景一致，我們發現Li₂O（以及Na₂O、K₂O和Rb₂O）採用反螢石結構（8:4 配位 - 見問題 8.8.2），我們預計會發現相對離子性的M₂X 化合物。然而奇怪的是，Cs₂O 在反CdCl₂ 結構中結晶。這很奇怪，因為CdCl₂ 具有層狀結構，我們通常將其與極性共價MX₂ 化合物相關聯（見第 8.4 節）。在Cs₂O 中，六個Cs⁺ 陽離子以八面體形式包圍每個O^2- 陰離子。每個Cs⁺ 與三個O^2- 離子配位，Cs⁺ 離子在範德華間隙中相互接觸。Cs⁺ 離子彼此靠近顯然在靜電上是不利的，那麼為什麼Cs₂O 更喜歡反CdCl₂ 結構而不是反螢石結構呢？

答案與鹼金屬離子圍繞氧的擁擠有關，如右圖所示的K₂O。由於八個較大的K⁺ 離子包圍每個O^2- 離子，因此陽離子基本上是相互接觸的。實際上，在Na₂O、K₂O 和Rb₂O 中，金屬-氧鍵相對於其他結構中具有相同鍵序的M-O 鍵而言是“拉伸”的。 Cs₂O 的情況非常極端，因此它找到了一種（靜電上不利的）結構，其中配位降低為 6:3。這種堆積問題在過氧化物中得到一定程度的緩解，在過氧化物中配位仍然是 8:4，但陰離子更大，特別是在超氧化物中，陽離子：陰離子比率為 1:1，配位為 6:6。因此，較大的鹼金屬離子（K⁺、Rb⁺、Cs⁺）傾向於形成超氧化物。

我們可以透過形成氧化物、過氧化物和超氧化物的能量學來解釋這種趨勢的另一種方法。

讓我們計算一下從金屬和氧氣形成金屬氧化物M₂O（每摩爾金屬）的焓變。

M(s) + 1/4 O₂(g) --> 1/2 M₂O(s)

我們可以使用赫斯定律將其寫成反應的總和

反應	ΔH
M(s) --> M(g) --> M+(g)	ΔHs + IE = ΔHf,M+(g)
1/4 O2(g) --> 1/2 O(g) --> 1/2 O2-(g)	1/4 ΔHd + 1/2 EA1 + 1/2 EA2 = 1/2 ΔHf,O2-(g)
M+(g) + 1/2 O2-(g) --> 1/2 M2O(s)	1/2 EL,M2O - 3/2 RT
總計
M(s) + 1/4 O2(g) --> 1/2 M2O(s)	ΔHf,M+(g) + 1/2 ΔHf,O2-(g) + 1/2 EL,M2O - 3/2 RT

為了得到總反應的焓變（1/2 摩爾 M₂O 的生成熱），我們需要M⁺(g) 和O^2-(g) 的生成熱，這些熱值可以從表格中獲得，以及E_L，我們可以用卡普斯廷斯基方程計算。

類似地，我們可以寫出鹼金屬過氧化物的形成

M(s) + 1/2 O₂(g) --> 1/2 M₂O₂(s)

反應	ΔH
M(s) --> M(g) --> M+(g)	ΔHf,M+(g)
1/2 O2(g) --> 1/2 O22-(g)	1/2 ΔHf,O22-(g)
M+(g) + 1/2 O22-(g) --> 1/2 M2O2(s)	1/2 EL,M2O2 - 3/2 RT
總計
M(s) + 1/2 O2(g) --> 1/2 M2O2(s)	ΔHf,M+(g) + 1/2 ΔHf,O22-(g) + 1/2 EL,M2O2 - 3/2 RT

以及超氧化物

M(s) + O₂(g) --> MO₂(s)

反應	ΔH
M(s) --> M(g) --> M+(g)	ΔHf,M+(g)
O2(g) --> O2-(g)	ΔHf,O2-(g)
M+(g) + O2-(g) --> MO2(s)	EL,MO2 - 2 RT
總計
M(s) + O2(g) --> MO2(s)	ΔHf,M+(g) + ΔHf,O2-(g) + EL,MO2 - 2 RT

對於氣態陰離子和陽離子，我們有以下生成熱和離子半徑（CN=6）

離子	ΔHf, kJ	離子半徑，Å
Li+	678	0.76
Na+	602	1.02
K+	506	1.38
Rb+	485	1.52
Cs+	473	1.67
O2-	500	1.20
O22-	519	1.59
O2-	-88	1.49

現在使用卡普斯廷斯基方程，我們可以計算出每種化合物的晶格能；這些晶格能已透過減去 2 RT 或 3 RT（根據需要）轉換為晶格焓

$\mathbf {E} _{L}={1213.8z_{+}z_{-}n \over r_{+}+r_{-}}(1-{\frac {0.345}{r_{+}+r_{-}}})$

金屬	ΔHL,M2O	ΔHL,M2O2	ΔHL,MO2
Li	-3,065 kJ	-2,651 kJ	-918 kJ
Na	-2,776	-2,433	-838
K	-2,454	-2,178	-751
Rb	-2,345	-2,090	-721
Cs	-2,241	-2,007	-678

正如預期的那樣，M₂O 和M₂O₂ 的晶格能相當，後者的大小略小一些，因為O₂^2- 陰離子的尺寸更大。超氧化物MO₂ 的晶格能大約是相應過氧化物晶格能的 1/3，因為陰離子和陽離子都是單電荷的，並且每個化學式單位中只有兩個離子。

現在，將所有這些放在一起，我們可以使用晶格能和單個離子的生成熱來比較每種氧化物的生成熱（每摩爾金屬）

金屬	1/2 ΔHf,M2O	1/2 ΔHf,M2O2	ΔHf,MO2
Li	-404 kJ	-388 kJ	-328 kJ
Na	-338	-354	-324
K	-271	-321	-328
Rb	-241	-300	-324
Cs	-53	-70	-81

我們可以看到，對於Li，Li₂O 的形成優於Li₂O₂ 或LiO₂，因為Li₂O 的晶格能非常有利。隨著晶格能隨著陽離子尺寸的增加而變得越來越不負，過氧化物在Na處變得最穩定。對於較重的鹼金屬，M₂O 變得很不穩定，超氧化物MO₂ 最穩定。這與我們對第一族氧化物化學性質的觀察結果一致。

Rb₉O₂ 簇在Rb 次氧化物中

鹼金屬次氧化物。有趣的是，最重的鹼金屬（Rb、Cs）也形成一系列次氧化物，例如Rb₉O₂、Rb₆O、Cs₁₁O₃、Cs₄O、Cs₇O、Cs₁₁O₃Rb、Cs₁₁O₃Rb₂ 和Cs₁₁O₃Rb₃，其中氧化物離子被鹼金屬以八面體形式配位。富含金屬的化學計量（例如，Rb₆O 和Cs₇O）是這些簇與鹼金屬的晶體共生。 這些化合物是有效的還原劑。

呼吸空氣鋰電池示意圖

金屬-空氣電池。鹼金屬氧化物在金屬-空氣電池的背景下非常有趣，因為它們在質量基礎上具有極高的儲能潛力。此類電池具有鹼金屬（通常為 Li）或 Zn 負極，並在正極利用空氣中的氧氣。雖然鋰是最輕的，因此也是能量密度最高的鹼金屬，但在電池充電時，與鋰枝晶的形成以及正極上O₂(g) 和2 O^2- 之間四電子相互轉化的緩慢動力學有關的材料問題。出於這個原因，目前正在研究超氧化物電池作為替代方案。單電子正極反應O₂ + e^- = O₂^- 的動力學很快，鉀 和鈉 代表了這些呼吸空氣電池負極鋰的潛在可行替代品。最近，已經證明LiO₂ 可以透過在銥奈米粒子上的模板生長而動力學穩定，這有可能為非常高能量密度的鋰空氣電池開啟大門。

  9.11 晶格能和溶解度

晶格能也可以幫助預測化合物溶解度。讓我們考慮一下將鹽溶解在水中的玻恩-哈伯迴圈。我們可以將其想象成兩個過程的總和：（1）鹽汽化以產生氣態離子，以晶格焓為特徵，以及（2）這些離子的水合作用以產生溶液。整個過程的焓變是這兩個步驟的總和。我們知道固體溶解的熵變是正的，因此溶解度取決於整個過程的焓變。

這裡我們需要考慮晶格能 E_L 和水合能 E_H 的趨勢。晶格能取決於陰離子和陽離子半徑之和 (r₊ + r_-)，而水合能則有單獨的陰離子和陽離子項。一般來說，由於 1/r² 依賴性，小離子（通常是陽離子）的溶劑化占主導地位。

$E_{L}\propto {\frac {1}{r_{+}+r_{-}}}$

$E_{H}\propto {\frac {1}{r_{+}^{2}}}+{\frac {1}{r_{-}^{2}}}$

對於含有較大陰離子的鹽，當 r₊ 變化時，E_L 不會發生太大變化。這是因為陰離子在 E_L 公式的分母中的 r₊ + r_- 項中占主導地位。另一方面，E_H 隨著 r₊ 的變化而發生顯著變化，特別是對於小的陽離子。

因此，小的二價陽離子的硫酸鹽，如 MgSO₄（瀉鹽），是可溶的，而 BaSO₄ 中 Ba²⁺ 的水合能較低，使得該鹽不溶（K_sp = 10^-10）。

左圖：硫酸鹽的 E_L 圖。大的 SO₄^2- 離子與小的陽離子（如 Mg²⁺）的大小不匹配，這些陽離子的水合能很高，從而形成可溶性鹽。對於較大的陽離子（如 Ba²⁺），其 E_H 較低，晶格能超過溶劑化焓，因此鹽不溶。右圖：在小陰離子（如 F^- 和 OH^-）的情況下，晶格能與小的陽離子（如過渡金屬離子 (TMⁿ⁺)、Mg²⁺ 和 Li⁺）占主導地位。陰離子和陽離子的大小不匹配發生在較大的陽離子（如 Cs⁺ 和 Ba²⁺）中，這些陽離子會形成可溶性氟化物鹽。

對於小的陰離子，E_L 對 r₊ 更敏感，而 E_H 對 r₊ 的依賴性不那麼強。對於氟化物和氫氧化物，LiF 稍微可溶，而 CsF 非常可溶，Mg(OH)₂ 不溶，而 Ba(OH)₂ 非常可溶。

將這兩種趨勢結合起來，我們發現，低溶解度最常出現在陰離子和陽離子在尺寸上良好匹配的情況下，特別是當其中一個或兩個都具有多重電荷時。

空間填充模型顯示了 Ba²⁺ 和 SO₄^2- 的範德華表面。兩種離子的尺寸相似有助於 BaSO₄ 在水中的低溶解度。

結合我們對溶解度的所有結論，我們注意到以下趨勢

1) 陰離子和陽離子之間的尺寸不匹配增加會導致更高的溶解度，因此 CsF 和 LiI 是鹼金屬鹵化物中最可溶的。

2) 共價性增加會導致鹽的溶解度降低（由於 E_L 更大）。例如，AgF、AgCl、AgBr 和 AgI 的溶解度逐漸降低，因為共價性增加。

AgF > AgCl > AgBr > AgI

3) 陰離子電荷增加會導致溶解度降低，因為 E_L 的增加相對於 E_H 的增加較大。

4) 小的、多價陽離子（具有較大的 E_H）會與大的、單價陰離子形成可溶性鹽，如 I^-、NO₃^-、ClO₄^-、PF₆^- 和乙酸根。

例子：過渡金屬和鑭系元素離子的鹽

• Ln³⁺：硝酸鹽可溶，但氧化物和氫氧化物不溶。

• Fe³⁺：高氯酸鹽可溶，但硫酸鹽不溶。

5) 多重電荷陰離子，如 O^2-、S^2-、PO₄^3- 和 SO₄^2-，會與大多數 M²⁺、M³⁺ 和 M⁴⁺ 金屬形成不溶性鹽。

  9.12 討論問題

• 解釋為什麼晶格能計算對於 NaCl 和 CaCl₂ 非常準確，但對於 AgCl 和 PbCl₂ 卻不太準確（大約 10%）。Born-Mayer 方程是否低估或高估了後者的值？
• 氟的電負性比氧更高。然而，對於許多過渡金屬，我們可以在氧化物中形成比在氟化物中更高的氧化態。例如，Mn(IV) 在氧化物 (MnO₂) 中是穩定的，但 MnF₄ 相對於 MnF₃ 和氟是不穩定的。^[22] 你能用晶格能來解釋這一點嗎？

  9.13 問題

1. 利用晶格能解釋為什麼 MgSO₄ 在比 BaSO₄ 低得多的溫度下分解成氧化鎂和 SO₃。

2. 當鈉金屬被氧化時，最容易形成的氧化物不是 Na₂O，而是過氧化物 Na₂O₂，我們可以將其表示為 (Na⁺)₂(O₂^2-)。鈣離子的電負性 (1.0) 和離子半徑 (1.14 Å) 非常接近鈉的電負性 (0.9) 和離子半徑 (1.16 Å)。你認為鈣暴露在空氣中會形成氧化物 (CaO) 還是過氧化物 (CaO₂)？解釋你的推理。

3. 固體 CaO 可以表示為 Ca⁺O^- 或 Ca²⁺O^2-。使用下面的熱化學資料（其中一些與問題無關）和 Kapustinskii 公式來確定哪種更穩定。CaO 的晶格常數（NaCl 結構）為 4.810 Å。雖然 O^- 離子的想法可能看起來很奇怪，但請注意，O 的第二次電子親和能和 Ca 的第二次電離勢（在下表中）都是相當吸熱的。

反應	∆Ho，kJ/mol
Ca(s) = Ca(g)	178
Ca(g) = Ca+(g) + e-	590
Ca+(g) = Ca2+(g) + e-	1,145
O2(g) = 2 O(g)	498
O(g) + e- = O-(g)	-141
O-(g) + e- = O2-(g)	790

4. 從固體 NH₄Cl 的生成熱 (-315 kJ/mol) 和氣態 NH₃ 的生成熱 (-46)、H₂ 的鍵解離能 (436) 和 Cl₂ 的鍵解離能 (244)、原子氫的電離勢 (1,311) 和原子氯的電子親和能 (-349) 中，計算 NH₃ 的氣相質子親和能。NH₄Cl 的晶格能可以透過 Kapustinskii 公式估計，使用 r_N-Cl = 3.50 Å。

5. 氨水瓶通常標註為“氫氧化銨”。我們將透過使用晶格能計算來檢驗這一觀點，以確定 NH₄⁺OH^- 鹽是否可以存在。

氣態 OH- 和 H₂O 的生成熱分別為 -141 和 -242 kJ/mol。假設 NH₄⁺ 的大小與 Rb⁺ 相似，而 OH^- 的大小與 F^- 相似，使用 Kapustinskii 公式、離子半徑和問題 4 中計算的 NH₃ 質子親和能，確定 NH₄⁺OH^- 相對於 NH₃ 和 H₂O 是否應該是一種穩定的鹽。在什麼溫度下 NH₄⁺Cl^- 相對於 NH₃ 和 HCl 應該是不穩定的，如果 HCl 的 ΔH_f^o 為 -92 kJ/mol，而 ΔS^o (NH₄Cl --> NH₃ + HCl) = 280 J/mol K？

6. 鋰金屬在氮氣中燃燒生成氮化鋰 Li₃N。較重的鹼金屬 (K、Rb、Cs) 可以形成穩定的疊氮化物 (MN₃)，但不能形成 M₃N 氮化物。解釋為什麼是這樣。

7. (a) 你認為 BaSO₄ 還是 MgSO₄ 在水中的溶解度更高？(b) LiF 的溶解度是否高於 LiClO₄？解釋。

8. 你認為 ZnS 的哪種多晶型（閃鋅礦或纖鋅礦）在靜電能方面更穩定？

9. 地下水中的砷汙染是孟加拉國、智利、阿根廷以及美國西部等世界各地的一個嚴重問題。在恆河三角洲，砷中毒十分普遍，因為抽水機從地下 20-100 米處抽取受汙染的水。人們提出的一種簡單的處理方法是透過對井水進行曝氣來沉澱砷，井水中也含有高濃度的 Fe²⁺。參考右側的砷 Pourbaix 圖和第 4 章中鐵的 Pourbaix 圖，確定在中性 pH 下曝氣水中存在的鐵和砷物種。什麼不溶性化合物會沉澱下來以降低砷的濃度？(提示：哪種化合物的晶格能最大？)