無機化學導論/分子軌道理論

第2章：分子軌道理論

一氧化碳分子中最低未佔分子軌道是一個 π 反鍵軌道，它來自碳（左）和氧（右）的 2p 軌道

價鍵理論（VB）為我們提供了化學鍵合的定性影像，這對於預測分子形狀、鍵強度等非常有用。它不能準確描述一些鍵合情況，因為它忽略了電子的波動性。

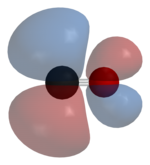
分子軌道理論（MO）具有更定量的潛力。利用它，我們還可以獲得電子在分子中的位置影像，如右側影像所示。這可以幫助我們理解其他難以解釋的鍵合和反應模式。

儘管 MO 理論原則上為我們提供了一種非常精確地計算電子在分子中的能量和波函式的方法，但通常我們也採用簡化的模型。這些簡單模型並沒有給出非常精確的軌道和鍵能，但它們確實解釋了共振等概念（例如，在二茂鐵分子中），這些概念在其他情況下難以表示。我們可以透過計算“數值計算”從 MO 理論獲得更精確的能量。許多商業和開源的程式已經開發出來，用於精確計算分子和擴充套件固體的電子結構。

雖然 MO 理論比 VB 理論更正確，並且可以非常準確地預測分子的性質，但即使對於相當簡單的分子，它也相當複雜。例如，你應該毫不費力地畫出 CO、NH₃ 和苯的 VB 影像，但我們會發現，隨著 MO 理論的發展，這些影像會越來越具有挑戰性。

第 2 章的學習目標

• 能夠為同核雙原子、異核雙原子、同核三原子和異核三原子分子構建分子軌道圖。
• 理解並能夠闡明分子軌道形成的方式——概念上、視覺上、圖形上和（半）數學上。
• 將雙原子和三原子分子的鍵序、鍵長和鍵強度聯絡起來，包括中性形式和離子形式。
• 利用分子軌道理論預測簡單三原子體系的分子幾何形狀。
• 根據軌道重疊和鍵合，合理化幾個特定體系的分子結構。
• 理解具有 π 鍵合的分子中芳香性和反芳香性的起源。

  2.1 從原子軌道構建分子軌道

分子軌道理論涉及（近似地）求解分子中電子的薛定諤方程。回顧第 1 章，這是一個微分方程，其中右側的第一項和第二項分別代表動能和勢能。

$E\psi =-{\frac {\hbar ^{2}}{2\mu }}\nabla ^{2}\psi +V\psi$

雖然薛定諤方程可以針對氫原子進行解析求解，但當分子中存在多個（相互排斥）電子時，勢能函式 V 會變得更加複雜——然後方程只能進行數值求解。因此，作為第一個近似值，我們將假設構成分子的原子的 s、p、d、f 等軌道是薛定諤方程的良好解。然後，當我們將原子結合在一起形成鍵時，我們可以允許這些波函式發生相長和相消干涉。這樣，我們利用原子軌道（AO）作為構建 MO 的基礎。

LCAO-MO = 原子軌道線性組合。 在物理學中，這被稱為緊束縛近似。

我們實際上以前在第 1 章構建雜化軌道時就見過原子軌道的線性組合。我們為雜化開發的基本規則也適用於這裡：軌道以標量係數 (c) 相加，使得所得軌道是正交的和歸一化的。不同之處在於，在 MO 情況下，原子軌道來自不同的原子。

原子軌道的線性組合總是返回相同數量的分子軌道。因此，如果我們從兩個原子軌道開始（例如，一個 s 和一個 p_z 軌道，如圖 2.1.1 所示），我們最終會得到兩個分子軌道。當原子軌道同相相加時，我們得到相長干涉和較低能量的軌道。當它們反相相加時，我們得到一個節點，所得軌道具有更高的能量。較低能量的 MO 是成鍵的，較高能量的 MO 是反鍵的。

圖 2.1.1。s 和 p 軌道的 σ 成鍵和反鍵組合

圖 2.1.2。內皮細胞的不同成分用藍色、綠色和紅色熒光染料染色。對於每種染料，發射光的顏色對應於電子從分子的 LUMO 降至 HOMO 時釋放的能量。

分子軌道也稱為波函式（ψ），因為它們是分子薛定諤方程的解。原子軌道（也稱為基函式）標記為 φ，例如，φ_1s 和 φ_3pz 或簡稱為 φ₁ 和 φ₂。

原則上，我們需要針對分子中的所有軌道求解薛定諤方程，然後像我們對原子中的軌道那樣，用電子對填充它們。在實踐中，我們實際上只對源於組成原子價軌道的 MO 感興趣，因為這些是參與鍵合的軌道。我們特別感興趣的是前沿軌道，即最高佔據分子軌道（HOMO）和最低未佔分子軌道（LUMO）。能量低得多的填充軌道（即核心軌道）不參與鍵合，能量更高的空軌道也不參與鍵合。然而，這些軌道在光化學和光譜學中很重要，光化學和光譜學涉及從佔據軌道到空軌道的電子躍遷。如圖 2.1.2 所示，使細胞染色的熒光染料透過將 HOMO 中的電子提升到空 MO 來吸收光，並在電子降回原始能級時發出光。

作為 LCAO-MO 方法的一個例子，我們可以從兩個 AO φ₁ 和 φ₂（圖 2.1.1）構建 HCl 分子的兩個 MO（ψ₁ 和 ψ₂）。為了進行這兩種線性組合，我們寫道

$\psi _{1}=c_{1}\phi _{1}+c_{2}\phi _{2}$

以及

$\psi _{2}=c_{1}\phi _{1}-c_{2}\phi _{2}$

當構成它們的兩個原子軌道 (AO) 相同時，係數 c₁ 和 c₂ 將相等（或幾乎相等），例如，當兩個氫 1s 軌道組合形成 H₂ 中的成鍵和反鍵分子軌道 (MO) 時。當 AO 之間存在能量差時，它們將不相等，例如當氫 1s 軌道和氯 3p 軌道組合形成極性 H-Cl 鍵時。

節點

波函式 φ 和 ψ 是振幅，與在空間某一點找到電子的機率有關。它們有帶 (+) 或 (-) 符號的瓣，我們用陰影或顏色來表示。在波函式改變符號的地方，我們有一個節點。正如您在圖 2.1.1 中看到的，MO 中的節點是由於 (+) 和 (-) 波函式的相消干涉造成的。通常，節點越多，軌道的能量越高。

在上面的例子中，我們畫出了 Cl 3p_z 軌道的簡化圖以及由此產生的 MO，省略了徑向節點。回想一下，2p 軌道沒有徑向節點，3p 軌道有一個，如圖 2.1.3 所示。4p 軌道有兩個徑向節點，依此類推。我們透過組合 AO 製成的 MO 也具有這些節點。

圖 2.1.3。2p 和 3p 軌道的節點結構

歸一化：我們將波函式平方以獲得機率，機率總是正數或零。因此，如果一個電子在軌道 φ₁ 中，找到它在點 xyz 的機率是 φ₁(x,y,z) 的平方^[1]。當我們組合 AO 製成 MO 時，總機率不會改變，因此對於組合 φ₁ 和 φ₂ 製成 ψ₁ 和 ψ₂ 的簡單情況，

$\psi _{1}^{2}+\psi _{2}^{2}=\phi _{1}^{2}+\phi _{2}^{2}$

圖 2.1.4。原子軌道的波函式隨距離呈指數衰減。當兩個原子靠得很近時，軌道重疊不為零，如上圖中 1s 軌道的示意圖所示。下圖顯示了距離太遠而無法相互作用的軌道。在這種情況下，S 和 β 都接近零。

重疊積分

兩個原子軌道 φ₁ 和 φ₂ 之間的空間重疊由重疊積分 S 描述，

$S_{12}=\int \phi _{1}^{*}\phi _{2}\,\mathrm {d} \tau$

其中積分是在整個空間上 ($\mathrm {d} \tau =\mathrm {d} x\,\mathrm {d} y\,\mathrm {d} z$).

成鍵和反鍵 MO 的能量

成鍵和反鍵軌道的能量強烈依賴於原子之間的距離。圖 2.1.5 針對氫分子 H₂ 說明了這一點。在很長的距離上，H 1s 軌道的同相和異相組合之間基本上沒有能量差異。隨著它們越來越靠近，同相（成鍵）組合的能量下降，因為電子在兩個帶正電的原子核之間共享。能量在平衡鍵長 (0.74 Å) 處達到最小值，然後隨著原子核越來越靠近，能量再次上升。反鍵組合在原子核之間有一個節點，因此它的能量隨著原子核的靠近而不斷上升。

圖 2.1.5。H₂ 分子成鍵和反鍵軌道的能量隨距離的變化

在平衡鍵長處，成鍵和反鍵分子軌道的能量 (ψ₁, ψ₂) 分別低於和高於原子基軌道的能量 φ₁ 和 φ₂。圖 2.1.6 顯示了 H₂ 分子的 MO 的情況。

圖 2.1.6。H₂ 分子的分子軌道能級圖

一個電子在原子軌道中的能量是 α，即庫侖積分。

$\alpha =\int \phi _{1}^{*}H\phi _{1}\,\mathrm {d} \tau =\int \phi _{2}^{*}H\phi _{2}\,\mathrm {d} \tau$

其中 H 是哈密頓算符。本質上，α 代表原子軌道 φ₁ 或 φ₂ 中電子的電離能。

AO 和 MO 之間的能量差由交換積分 β 決定，

$\beta =\int \phi _{1}^{*}H\phi _{2}\,\mathrm {d} \tau$

β 是一個重要的量，因為它告訴我們分子鍵能的資訊，以及成鍵和反鍵軌道之間的能量差。對於多電子分子，計算 β 並不容易，因為我們無法解析地求解薛定諤方程以獲得波函式。但是，我們可以進行一些近似來數值計算能量和波函式。在休克爾近似中，它可用於獲得有機分子中 π 分子軌道的近似解，我們透過令 S=0 並對任何彼此不相鄰的 p 軌道令 H=0 來簡化數學。擴充套件休克爾方法^[2]，由羅爾德·霍夫曼開發，以及其他半經驗方法可用於快速獲得各種分子和擴充套件固體的相對軌道能量、近似波函式和分子軌道簡併性。現在在軟體包中可以輕鬆獲得更復雜的從頭算方法，可用於計算分子和固體的精確軌道能量。

我們可以透過應用歸一化條件得到氫分子的係數 c₁ 和 c₂

$\psi _{1}={\frac {1}{\sqrt {2}}}{\frac {\phi _{1}+\phi _{2}}{1+S}}\qquad {\text{(bonding orbital)}}$

以及

$\psi _{1}={\frac {1}{\sqrt {2}}}{\frac {\phi _{1}-\phi _{2}}{1-S}}\qquad {\text{(antibonding orbital)}}$

當 S≈0 時，我們可以消除 1-S 項，兩個係數都變為 1/√2

請注意，H₂ 的 MO 圖中的成鍵軌道被穩定了 β/(1+S) 的能量，而反鍵軌道被不穩定了 β/(1-S) 的能量。也就是說，反鍵軌道在能量上比成鍵軌道下降更多。這意味著 H₂ (ψ₁²ψ₂⁰) 在能量上比兩個 H 原子更穩定，但 He₂ 具有四個電子 (ψ₁²ψ₂²) 相對於兩個 He 原子來說是不穩定的。

鍵級：在任何 MO 圖中，鍵級可以計算為 ½ (成鍵電子數 - 反鍵電子數)。對於 H₂，鍵級為 1，對於 He₂，鍵級為零。

鍵強度和鍵長：當我們使用 MO 理論計算鍵時，我們使用上面的公式來計算淨鍵級。這個公式意味著 H₂⁺ 和 H₂^- 分子都具有 1/2 的鍵級，因為有一個淨成鍵電子。然而，在實驗中，我們發現 H₂^- 中的鍵比 H₂⁺ 中的鍵長得多，也弱得多。下表總結了僅使用它們的 1s 原子軌道形成 σ 和 σ* 分子軌道的分子和離子的鍵強度和鍵長。

雙原子分子和離子的 MO 配置、鍵長和鍵強度

分子	電子數	MO 配置	淨成鍵電子數	鍵級	鍵長 (Å)	鍵能 (kJ/mol)
H2+	1	σ1s1	1	1/2	1.07	256
H2	2	σ1s2	2	1	0.74	436
H2-	3	σ1s2σ*1s1	1	1/2	-	156
He2+	3	σ1s2σ*1s1	1	1/2	1.08	230
He2	4	σ1s2σ*1s2	0	0	-	-

H₂⁺ 和 H₂^- 中鍵強度之間顯著差異的出現是由於三電子 H₂^- 離子中存在電子-電子排斥，而在 H₂⁺ 中不存在電子-電子排斥。我們還觀察到，三電子 He₂⁺ 離子的鍵比 H₂^- 中的鍵強得多。在 He₂⁺ 的情況下，電子與 He²⁺ 核的正電荷之間的吸引力抵消了電子-電子排斥。故事的寓意是，我們繪製的 MO 圖（就像我們從薛定諤方程繪製的原子軌道一樣）是針對單電子原子計算的，但在真實的（多電子）原子和分子中，我們在估計或計算鍵能時必須考慮電子-電子排斥。

異核情況（例如，HCl） - 極性鍵

這裡我們引入了構成化學鍵的兩個原子之間的電負性差異。H 1s 軌道中電子的能量高於 Cl 3p_z 軌道中電子的能量（更容易電離）。這導致形成的分子軌道 ψ₁ 和 ψ₂ 之間的能量差更大，如圖 2.1.7 所示。原子軌道之間電負性差異越大（Δα 越大），成鍵軌道就越具有“φ₂ 特徵”，即在這種情況下的 Cl 3p_z 軌道越相似。這與 H-Cl 具有極性單鍵的想法一致：兩個電子駐留在主要定位在 Cl 原子上的成鍵分子軌道中。

圖 2.1.7. HCl 分子的分子軌道能級圖

反鍵軌道（空）具有更多的 H 特徵。鍵級仍然為 1，因為成鍵軌道中有兩個電子，而反鍵軌道中沒有電子。

極端情況 - 離子鍵 (NaF)：非常大的 Δα

在這種情況下，AO 之間沒有太多混合，因為它們的能量相差很遠（圖 2.1.8）。兩個成鍵電子都位於 F 原子上，因此我們可以將分子寫成 Na⁺F^-。請注意，如果我們使用光將電子從 ψ₁ 激發到 ψ₂，則得到的電子構型將是 (ψ₁¹ψ₂¹)，我們將有 Na⁰F⁰。這被稱為電荷轉移躍遷。

圖 2.1.8. 說明 NaF 分子中離子鍵的分子軌道能級圖

到目前為止，分子軌道理論的總結

• 加減 AO 波函式以構成 MO。兩個 AO → 兩個 MO。更一般地說，MO 的總數等於 AO 基組軌道的數目。

• 我們展示了最簡單的情況（只有兩個基組軌道）。更精確的計算使用更大的基組（更多 AO），並使用哈密頓算符 H 的勢能函式的數學友好近似值來求解給出最低總能量的 c 矩陣。

• 更多節點 → 更高能量 MO

• 鍵級 = ½ (成鍵電子數 - 反鍵電子數)

• 鍵極性 在 MO 影像中表現為軌道“特徵”。

• 能量相差很遠 的 AO 在結合形成 MO 時不會發生太多相互作用。

  2.2 軌道對稱性

圖 2.2.1. σ 對稱性的示例。

當涉及到許多價 AO 時，分子的 MO 影像會變得複雜。我們可以透過注意到（這裡沒有證明）不同對稱性的軌道（相對於分子）不會相互作用，從而極大地簡化問題。分子的對稱操作（可以包括旋轉、鏡面、反轉中心等），以及分子中鍵和軌道的對稱性類別，可以根據群論進行嚴格定義。在這裡，我們將採用一種簡單的方法來解決這個問題，該方法基於我們對三維物體的對稱性的直觀理解，如圖 2.2.1 所示。

AO 必須具有相同的節點對稱性（由分子對稱操作定義），否則它們的重疊為零。

例如，在 HCl 分子中，有一個獨特的對稱軸 →，它通常定義為笛卡爾 z 軸，如圖 2.2.2 所示。

圖 2.2.2. 具有 σ 和 π 對稱性的軌道不會相互作用。

從該圖中我們可以看出，H 1s 軌道在繞鍵軸旋轉 180° 時保持不變。然而，相同的旋轉會反轉 Cl 3p_y 波函式的符號。因為這兩個軌道具有不同的對稱性，所以 Cl 3p_y 軌道是非鍵的，並且不會與 H 1s 相互作用。Cl 3p_x 軌道也是如此。p_x 和 p_y 軌道具有 π 對稱性（包含鍵軸的節點平面），在 MO 能級圖中標記為 π_nb，如圖 2.2.3 所示。相反，H 1s 和 Cl 3p_z 軌道都具有 σ 對稱性，這也是圖 2.2.1 中所示的陶罐的對稱性。因為這些軌道具有相同的對稱性（在分子的點群中），所以它們可以形成圖 2.1.1 中所示的成鍵和反鍵組合。

包括 Cl 原子所有價軌道的 HCl 的 MO 圖示於圖 2.2.3 中。兩個 Cl 價軌道 (3p_x 和 3p_y) 具有錯誤的對稱性，無法與 H 1s 軌道相互作用。Cl 3s 軌道與 H 1s 具有相同的 (σ) 對稱性，但它的能量低得多，因此幾乎沒有軌道相互作用。因此，Cl 3s 軌道的能量僅受分子形成的輕微影響。因此，π_nb 和 σ_nb 軌道中的電子對是非鍵的。

圖 2.2.3. HCl 分子的能級圖，顯示了來自價 AO 的 MO。

請注意，圖 2.2.3 中的 MO 結果（1 個鍵和 3 對非鍵電子）與我們從 HCl 的價鍵理論中得到的相同。非鍵軌道定位在 Cl 原子上，正如我們從價鍵影像中推斷的那樣。

為了區分它與 σ 成鍵軌道，在這種情況下為空的 σ 反鍵軌道用星號表示。

  2.3 σ, π 和 δ 軌道

圖 2.3.1. 八氯二錸(III) 陰離子，[Re₂Cl₈]²⁻，它具有四重 Re-Re 鍵。

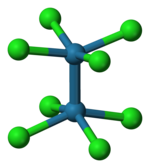
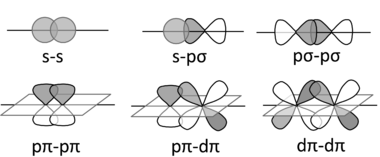
無機化合物使用 s、p 和 d 軌道（以及更少見的 f 軌道）來構成成鍵和反鍵組合。這些組合導致σ, π, 和 δ 鍵（以及反鍵）。

您已經熟悉了有機化合物中的 σ 和 π 鍵。在無機化學中，π 鍵可以由 p 和/或 d 軌道形成。δ 鍵比較少見，是由 d 軌道的面對面重疊形成的，例如在 Re₂Cl₈^2- 離子中。Cl 原子在該陰離子中重疊的事實是 δ 鍵存在的證據。

下面繪製了一些 s、p 和 d 軌道的 σ（頂行）、π（底行）和 δ 鍵合組合（右）。在每種情況下，我們都可以根據 AO 波函式的符號形成成鍵或反鍵組合。由於 pπ-pπ 鍵合涉及 p 軌道的側向重疊，因此它在第二週期元素（C、N、O）中最為常見。較重元素的 π 鍵化合物很少見，因為原子核較大，無法形成良好的 π 重疊。出於這個原因，含有 C=C 雙鍵的化合物非常常見，而含有 Si=Si 鍵的化合物則很少見。δ 鍵 通常比 σ 和 π 鍵弱得多。含有金屬-金屬 δ 鍵的化合物出現在過渡系列的中間。

    

過渡金屬 d 軌道也可以形成 σ 鍵，通常與配體上具有適當對稱性的 s-p 雜化軌道形成。例如，膦（R₃P:）是與過渡金屬形成配合物的良好 σ 供體，如右圖所示。

pπ-dπ 鍵合在過渡金屬配合物中也很重要。在金屬羰基配合物（如 Ni(CO)₄ 和 Mo(CO)₆）中，填充的金屬 d 軌道與 CO 分子的空 π 反鍵軌道（LUMO）之間存在側向重疊，如左側的圖所示。這種相互作用增強了金屬-碳鍵，但削弱了碳-氧鍵。C-O 紅外拉伸頻率是鍵強度診斷指標，可用於估算從金屬 d 軌道轉移到 CO π 反鍵軌道的電子數。

與膦配合物同樣存在這種反鍵合，膦配合物具有空 π 軌道，如右圖所示。含有鹵素配體的過渡金屬配合物也可能具有明顯的 pπ-dπ 鍵合，其中配體上的填充的 pπ 軌道將電子密度捐贈給未填充的金屬 dπ 軌道。我們將在第 5 章中遇到這些鍵合情況。

  2.4 雙原子分子

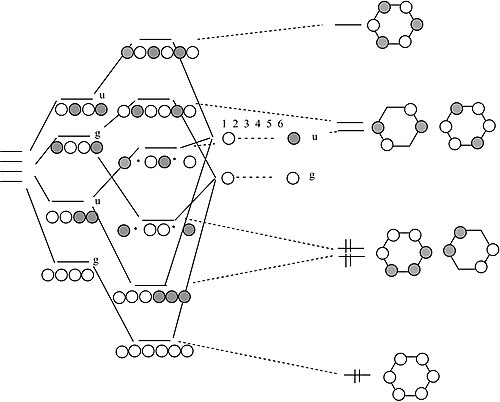
價鍵理論對於一些第二週期雙原子分子來說是失效的，最著名的例子是 O₂，它預測了一個反磁性的、雙鍵的分子，具有四個孤對電子。O₂ 確實具有雙鍵，但它在地面態具有兩個未配對電子，這種性質可以用 MO 圖來解釋。我們可以為這些分子構建 MO 能級圖，如下所示

                               Li₂, Be₂, B₂, C₂, N₂                                                         O₂, F₂, Ne₂

當 2s 和 2p AO 在能量上很好地分離時，我們得到了右側的更簡單的雙原子 MO 圖，如 O₂、F₂ 和 Ne₂。左側的圖是由 σ_2s 和 σ_2p MO 的混合產生的，這些 MO 在 Li₂、Be₂、B₂、C₂ 和 N₂ 中能量接近。這種混合的作用是將 σ_2s* 的能量降低，將 σ_2p 的能量提高，以至於 pπ 軌道位於 σ_2p 軌道下方。請注意，π 和 π* 軌道的能量不受 s-p 混合的影響，因為對稱性考慮因素。π 和 π* 軌道具有“u”對稱性，這意味著它們關於反轉操作是反對稱的。σ 和 σ* 軌道具有“g”對稱性，這意味著它們在反轉後保持不變（見第 2.5 節）。異核雙原子分子和離子（如 CO、NO 和 NO⁺）也由於 s-p 混合而具有左側所示的能級順序。

如果您想看看這些成鍵和反鍵分子軌道的樣子，可以在利物浦大學結構和鍵合網站上找到一個關於 CO 分子中的 MO 的良好動畫。

為什麼 O₂ 和 F₂ 不發生 sp 軌道混合？原因與軌道的能量有關，這些能量在左側的簡單影像中沒有按比例繪製。當我們從 Li 到 F 橫跨週期表的第二週期時，我們逐漸向原子核新增質子。2s 軌道在原子核處具有有限的幅度，因此它比 2p 軌道更“感受到”增加的核電荷。這意味著，當我們橫跨週期表（以及稍後我們將看到，當我們向下移動週期表時），s 軌道和 p 軌道之間的能量差變得很大，超過了鍵能。隨著 2s 和 2p 能量在能量上越來越遠離，軌道之間的相互作用（即混合）越來越少。

右側顯示了軌道能量圖。由於 1s 和 2s/2p 軌道之間的能量差非常大，因此我們將它們繪製在不同的能量尺度上，其中 1s 在左側，2s/2p 在右側。對於第二週期左側的元素（Li、Be、B），2s 和 2p 能量僅相差幾 eV。對於 O 和 F，能量差變得非常大——超過 20 電子伏特（1930 kJ/mol）。由於單鍵能通常約為 3-4 eV，因此這種能量差在我們的 MO 圖的尺度上將非常大。對於週期表第二週期的所有元素，1s（核心）軌道的能量比 2s/2p（價電子）軌道低得多，因此在繪製我們的 MO 圖時不需要考慮它們。

  2.5 軌道填充

根據泡利不相容原理和洪特規則，MO 從底部開始填充，就像我們對原子軌道所做的那樣。

問題：洪特規則的量子力學基礎是什麼？

考慮兩個簡併軌道的例子，例如第二週期雙原子分子中的 π 或 π* 軌道。如果這些軌道每個都包含一個電子，它們的自旋可以平行（洪特規則優先）或反平行。泡利不相容原理指出，一個軌道中不能有兩個電子具有相同的量子數集（n、l、m_l、m_s）。這意味著，在平行情況下，泡利不相容原理阻止電子訪問對方的軌道。在反平行情況下，它們可以自由地來去，因為它們具有不同的 m_s 量子數。然而，在同一個軌道中有兩個電子在能量上是不利的，因為同種電荷相互排斥。因此，平行排列，由於泡利不相容原理，具有更低的能量。

對於 O₂（12 個價電子），我們得到了下面的 MO 能級圖。右側顯示了分子軌道的形狀。

氧分子軌道圖

紅巨星的特點是它們大氣中存在 C₂ 分子。由於 C₂ 的淨鍵級為 2，因此它在從氣相冷卻到形成其他形式的碳（如富勒烯、石墨和金剛石）時會迅速反應，所有這些形式對於每兩個碳原子來說都有四個鍵。

這種 MO 的能量排序正確地預測了π* 軌道中存在兩個未配對電子，以及淨鍵級為 2（8 個成鍵電子和 4 個反鍵電子）。這與氧分子實驗觀察到的順磁性一致。

MO 理論對第二週期雙原子分子的其他有趣預測是，C₂ 分子的鍵級為 2，而 B₂ 分子具有兩個未配對電子（均已透過實驗驗證）。

我們還可以預測（使用上面的 O₂、F₂、Ne₂ 圖），NO 的鍵級為 2.5，CO 的鍵級為 3。

軌道標記中的“g”和“u”符號，我們只在中心對稱分子中使用，指的是它們關於反轉的對稱性。 gerade（g）軌道是對稱的，這意味著透過中心反轉不會改變軌道。 ungerade（u）表示軌道的符號在反轉操作中反轉。由於 g 和 u 軌道具有不同的對稱性，因此它們之間的重疊為零。正如我們將在下文中看到的那樣，根據 g 和 u 對稱性對軌道進行分解簡化了在更復雜的分子（如丁二烯和苯）中構建分子軌道的任務。

上面顯示的軌道形狀是使用分子的單電子模型計算得到的，就像我們對類氫原子軌道（AO）進行計算以獲得 s、p 和 d 軌道的形狀一樣。為了獲得多電子分子（即所有真實分子）的準確的分子軌道（MO）能量和圖，我們必須考慮電子是“關聯”的，也就是說，由於電子的負電荷，它們在分子中會互相避開。這個問題無法用解析方法求解，只能透過使用密度泛函理論（DFT）在數值計算中近似求解。我們將在第 10 章學習電子關聯在固體（例如超導體）中的影響。

  2.6 π 鍵的週期性趨勢

正如我們在第 2.3 節中提到的，pπ 鍵幾乎總是涉及第二週期元素。

我們在第二週期雙原子分子（B₂…O₂）的 MO 圖中遇到由 p 軌道側面重疊形成的 π 鍵。重要的是要記住，π 鍵比由相同 AO 形成的 σ 鍵弱，如果涉及第二週期以外的元素，則 π 鍵特別弱。

示例

乙烯和亞矽烷結構的比較

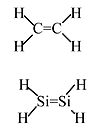
乙烯：穩定的分子，在沒有催化劑的情況下不會聚合。

亞矽烷：從未被分離出來，會自發聚合。計算表明，氣相中相對於單鍵（三重態）H₂Si-SiH₂ 的穩定性為 117 kJ/mol。

白磷 (P₄) 是一種軟的蠟狀固體，在空氣中會自燃，燃燒時發出明亮的火焰併產生大量的白色 P₄O₁₀ 煙霧。此處顯示的樣品是在水中拍攝的，以防止氧化反應。

Si 原子的巨大氖核抑制了 3p 軌道的側面重疊→ π 鍵很弱。

其他示例：P₄ 與 N₂

元素磷和氮結構的比較

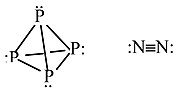
P 不能與自身形成 π 鍵，因此它形成具有顯著環張力的四面體分子。這種 P 的同素異形體在空氣中會自燃。固態白磷會非常緩慢地轉化為紅磷，這是一種更穩定的同素異形體，包含金字塔形 P 原子的片層，每個 P 原子與三個相鄰原子鍵合，並帶有一個孤對電子。

N 可以形成 π 鍵，因此 N₂ 具有非常強的三鍵，是一種相對惰性的雙原子氣體。

矽聚合物 (R₂SiO)_n 用於不粘炊具（如這些紙杯蛋糕模具）、橡皮泥、軟體機器人 和許多其他應用。

(CH₃)₂SiO 與 (CH₃)₂CO

聚矽氧烷和丙酮結構的比較

“RTV” 矽聚合物（Si 與 4 個單鍵鍵合）與丙酮（C=O 雙鍵）。矽樹脂是柔軟的、靈活的聚合物，可以在不分解的情況下加熱到高溫（>300 °C）。丙酮是一種易燃的分子液體，沸點為 56 °C。


另外比較
SiO₂ (mp ~1600°C) 與 CO₂ (在 -78°C 昇華)

S₈ (固體，環狀結構) 與 O₂ (氣體，雙鍵)

例外

第二週期元素可以與第三週期元素中最小的 P、S 和 Cl 形成相當強的 π 鍵。因此，我們在含硫氮化合物（如 S₂N₂ 和 S₃N₃^-）中發現 S=N 鍵，在磷酸和 P₄O₁₀（左側顯示）中發現 P=O 鍵，在 SO₂（與臭氧類似）中發現離域的 π 分子軌道。

  2.7 三中心鍵

我們使用 MO 理論解決的許多（但不是所有）問題都源於 H₂ 分子的 MO 圖（圖 2.1.5），這是一個雙中心鍵的情況。其他的問題我們將透過類比於 H₃⁺ 離子來解決，這引入了三中心鍵的概念。

我們可以用直線形或三角形幾何形狀來繪製 H₃⁺ 離子（以及 H₃ 和 H₃^-）。

H₃⁺ 的沃爾什相關圖

H₃⁺ 的沃爾什圖

關於此圖的一些重要要點

• 對於離子的直線形，最高和最低 MO 相對於分子中的反轉中心是對稱的。請注意，中心的 1s 軌道具有g 對稱性，因此根據對稱性，它與兩端兩個 1s 軌道的u 組合沒有重疊。這使得 σ_u 軌道成為非鍵合軌道。

• 在分子的三角形形狀中，源自 σ_u 和 σ*_g 的軌道變得簡併（即，根據對稱性，它們具有完全相同的能量）。術語符號“e”表示雙重簡併。我們將在後面看到，“t”表示三重簡併。請注意，我們放棄了三角形軌道的“g”和“u”，因為三角形沒有反轉中心。

• 三角形形狀最穩定，因為 H₃⁺ 中的兩個電子在最低軌道中具有較低的能量。彎曲分子會在兩端的 1s 軌道之間產生第三個鍵合相互作用。

XH₂ (X = Be, B, C…) 的 MO 圖

這比 H₃ 更復雜，因為 X 原子既有 s 軌道又有 p 軌道。但是，我們可以對軌道進行對稱性分解，並透過類比於 H₂ 分子來解決問題。

XH₂ 的 MO 圖

關於此 MO 圖的一些關鍵點

• 在具有反轉對稱性的分子的直線形中，X 原子的 2s 和 2p 軌道分解成三個對稱性類別

2s = σ_g

2p_z = σ_u

2p_x, 2p_y = π_u

• 類似地，我們可以看到，兩個 H 1s 軌道形成了兩個線性組合，一個具有 σ_g 對稱性，另一個具有 σ_u 對稱性。它們看起來像H₂ 分子的鍵合和反鍵合 MO（這就是我們說我們用這個問題來解決這個問題的原因）。

• π_u 軌道必須是非鍵合的，因為沒有 H 1s 軌道的組合具有 π_u 對稱性。

• 在 MO 圖中，我們製作了 σ_g 和 σ_u 的鍵合和反鍵合組合。對於 BeH₂，我們然後用四個價電子填充最低的兩個軌道，並發現（不出所料）分子具有兩個鍵，可以寫成H-Be-H。相關圖表明，分子的彎曲形狀應該不太穩定。

關於此 MO 圖的一個有趣的論點是，很難事先預測 CH₂ 應該是直線形還是彎曲形。1970 年，查爾斯·本德和亨利·謝弗使用量子化學計算預測，基態應該是一個彎曲的三重態，H-C-H 角為 135°。 當時最好的實驗表明亞甲基是一個線性單線態，理論學家認為實驗結果是錯誤的。後來的實驗證明他們是正確的！

“理論是沒有人相信的東西，除了提出它的人。實驗是每個人都相信的東西，除了做它的人。”——愛因斯坦

  2.8 構建更復雜分子的 MO：NH₃、P₄

NH₃ 的 MO 圖

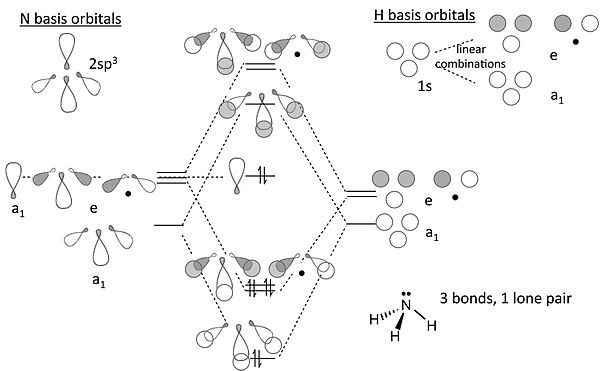
我們現在可以嘗試構建 NH₃ 的 MO 圖，以此為基礎，我們獲得了三角形 H₃⁺ 的結果。

氨分子的分子軌道圖

關於氨的 MO 圖的說明

• 從端面觀察，p 軌道或 sp_x 雜化軌道看起來就像 s 軌道。因此，我們可以使用我們在 s 軌道中（對於 H₃⁺）開發的解來建立氮 sp³ 軌道與 H 1s 軌道的 σ 鍵合和反鍵合組合。

• 我們現在構建氮原子的 sp³ 雜化軌道，並將它們定向，使得一個向上，另外三個形成四面體的三角形底座。後面三個，透過與 H₃⁺ 離子的類比，轉化為一個完全對稱軌道（“a₁”）和一個 e 對稱性對。位於四面體頂部的雜化軌道也具有 a₁ 對稱性。

• 三個氫 1s 軌道也形成了一個 a₁ 組合和一個（雙重簡併）e 組合。我們使用相同對稱性的氮軌道構建鍵合和反鍵合組合。N 上剩餘的 a₁ 軌道是非鍵合的。虛線顯示了 a₁ 和 e 對稱性的基軌道與分子軌道之間的關聯。

• 在 8 電子 NH₃ 分子中，結果是三個 N-H 鍵和一個孤對電子位於 N 上，這與價鍵理論相同（但工作量要多得多！）。

P₄ 分子和 P₄²⁺ 離子

透過與 NH₃ 的類比，我們可以構建 P₄ 四面體的一個頂點的 MO 圖，然後將結果乘以 4 來獲得整個分子的成鍵圖。一個重要的區別是 P₄ 中 s-p 雜化相對較少，因此孤對電子軌道具有更多的 s 特徵，能量低於主要由 pσ 構成的成鍵軌道。

P₄: 20 個價電子

P4 分子的分子軌道圖

移走 2 個電子形成 P₄²⁺

最高佔據分子軌道是成鍵軌道 → 斷開一條鍵，剩下 5 條鍵

方形形式減輕環張力，(60° → 90°)

P42+ 離子的結構

2 個 π 電子

芳香性 (4n + 2 規則)

  2.9 MO 圖中 σ 和 π 軌道的同源性

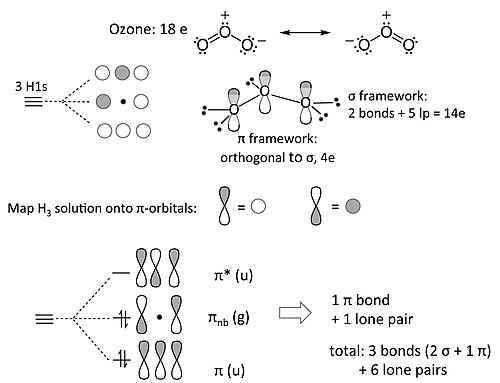
臭氧分子（以及包含三個非 H 原子的類似 18e 分子，例如 NO₂^- 和烯丙基陰離子 [CH₂-CH-CH₂]^-）是三中心四電子 π 成鍵的例子。我們對臭氧的 MO 處理完全類似於 4 電子 H₃^- 陰離子。我們將該解決方案對映到此解決方案上，如下所示

透過類比 H3- 構建臭氧的 π 系統

羅阿爾德·霍夫曼教授關於軌道對稱性的觀點幫助解釋了有機和有機金屬分子的成鍵和反應性，以及擴充套件固體的結構和性質。

非鍵合 π 軌道在中心 O 原子上有一個節點。這意味著 π 系統中的非鍵合電子對被兩個末端 O 原子共享，也就是說，形式電荷被這些原子共享。這與臭氧的八隅體共振結構一致。

將一組 s 軌道的解對映到 π 成鍵問題，這是一個簡單示例，它體現了一個更廣泛的原理，稱為等電子原理。這個想法由康奈爾大學的羅阿爾德·霍夫曼廣泛發展，已被用於理解有機金屬化合物中的成鍵和反應性。 <sup>在等電子原理中，對稱性原理（如上面 H₃- 和臭氧之間的類比所示）被用於從更簡單的分子片段構建包含 d 邊界軌道的複雜分子的 MO 圖。


三碘離子。 I₃- 是 3 中心 4 電子成鍵的類似（但似乎更復雜）的例子。每個 I 原子具有 4 個價軌道 (5s, 5p_x, 5p_y, 5p_z)，總共 12 個邊界軌道，而 I₃- 陰離子具有 22 個電子。

我們可以透過回憶兩個週期性趨勢來簡化問題</sup>

• 在週期表的第二週期之後，s-p 軌道分裂較大，相對於鍵能而言。因此，5s 軌道能量較低，並且收縮得過於緊密，無法與其鄰居形成鍵。
• 5p 軌道的 π 重疊非常弱，因此 5p_x 和 5p_y 軌道也將是非鍵合的。
  

這僅留下三個 5p_z 軌道來形成成鍵/非鍵合/反鍵組合。同樣，這個問題與臭氧或 H₃^- 完全類似。

從邊界 5pz 軌道構建 I3- MO 圖

計算軌道，我們從非鍵合 5s、5p_x 和 5p_y 軌道獲得 9 個孤對電子，以及從上面的 5p_z 軌道組合獲得 1 個鍵和 1 個孤對電子。總共 10 個非鍵合對和 1 個鍵解釋了離子中的 22 個電子。非鍵合 5p_z 對局域在末端 I 原子上，使每個原子的形式電荷為 -1/2。這個 MO 描述與我們在第 1 章中開發的 I₃^- 的八隅體無鍵共振影像完全一致。

  2.10 π 共軛體系的鏈和環

乙烯分子

        乙烯：π 系統類似於 H₂ 中的 σ 成鍵

H2 和乙烯軌道的同源性

從頂部或底部觀察，乙烯 π 軌道看起來像 H₂ σ 軌道。因此，我們可以將 H 原子鏈和環的解對映到 π 軌道鏈和環上（就像我們對 O₃ 的三軌道情況所做的那樣）。

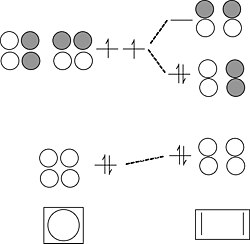
四個 H 原子或 π 軌道的鏈和環（H₄ 或丁二烯）

H4 或丁二烯的 MO 圖

關於這個 MO 圖的一些說明

• 線上性形式的分子中，AO 的組合形成一個階梯，具有均勻間隔的能級，交替排列為 g – u – g – u …。每個後續軌道都多一個節點。對於具有偶數個原子的 σ 或 π 軌道的線性鏈，這是一個通用的規則。

• 在分子的環狀形式中，底部有一個非簡併軌道，頂部有一個非簡併軌道，中間有一個簡併軌道階梯。對於具有偶數個原子的環狀分子，這也是一個通用的規則。這就是芳香族化合物4n+2 規則的起源。

• H₄ 有四個價電子，類比地，丁二烯有四個 π 電子。這些電子填充了分子線性形式的最低兩個 MO，對應於丁二烯中的兩個共軛 π 鍵 (H₂C=CH-CH=CH₂)。

• 在分子的環狀形式中，簡併軌道是單佔據的。分子可以透過扭曲成一個褶皺的矩形來打破簡併性（並降低能量）。對於反芳香族環狀分子（4n 規則），這是一個通用的規則。因此，環丁二烯應該是反芳香族，並且應該具有兩個單鍵和兩個雙鍵，它們沒有被共振離域。

環丁二烯的反芳香性

環丁二烯實際上是一個非常不穩定的分子，因為它會聚合以減輕環張力。該分子的空間位阻衍生物確實具有 MO 理論預測的褶皺矩形結構。

苯 π 軌道

我們如何從 4 原子鏈過渡到 6 原子鏈？

透過類比我們從 2 原子鏈過渡到 4 原子鏈的過程，我們現在從 4 過渡到 6。我們從 4 原子鏈的軌道開始，這些軌道形成一個 g 和 u 軌道的階梯。然後我們對我們正在新增在兩端的兩個原子進行 g 和 u 組合。透過將 g 與 g 相結合，將 u 與 u 相結合，我們最終得到 6 個原子的字串的解。將這些軌道閉合成一個迴圈，我們就得到了苯分子的 π 分子軌道。結果是三個 π 鍵，正如我們預期的那樣。苯符合 4n+2 規則 (n=2)，因此是芳香族化合物。

構建苯的 pi MO

在這裡，我們使用等電子原理從 s 軌道的組合構建了 π 鍵合體系的 MO 圖，例如乙烯和苯。它提出了一個有趣的問題，即芳香族 4n+2 規則是否可能適用於 s 軌道體系，即，如果三個 H₂ 分子可以結合在一起形成一個芳香族 H₆ 分子。事實上，最近在金剛石砧座中對超高壓下氫的研究表明，這樣的結構確實會形成。存在一個固態氫相，其中包含扭曲的六元環片，類似於在石墨或石墨烯中發現的完全連線的二維六元環網路。 <sup>具有四個成員環中六個 π 電子的陰離子也是芳香族化合物。例如，環丁烷的二陰離子 C₄H₄2-，以及 15 族陰離子 Bi₄2-、Sb₄2-、As₄2- 和 P₄2-。

現在應該從我們對四軌道和六軌道分子的 MO 圖的構建中很明顯，我們可以繼續新增原子軌道來形成 8、10、12... 原子的鏈和環。在每種情況下，g 和 u 軌道形成一個 MO 階梯。在 N 原子鏈階梯的底部，MO 中沒有節點，並且我們為每個階梯新增一個節點，直到我們到達頂部，在那裡有 N-1 個節點。另一種說法是，從底部算起的軌道 x 中電子的波長（1,2,3...x,...N）是 2Na/x，其中 a 是原子之間的距離。我們將在第 6 章和第 10 章中發現，我們可以從這個模型中瞭解很多關於金屬和半導體的電子性質，使用無限原子鏈作為晶體的模型。</sup>

  2.11 討論問題

二茂鐵

• 推匯出線性 H₂O 和彎曲 H₂O 的分子軌道圖。
• 解釋為什麼 H₂O 和 H₂S 的鍵角不同。
• 我們已經推導了四碳和六碳鏈和環的π體系的MO圖。重複此練習，針對五碳鏈和五碳環（例如，環戊二烯負離子），從H₂和H₃的MO影像開始。這個棘手的難題幫助我們理解了二茂鐵的電子結構，並獲得了1973年的諾貝爾獎。

  2.12 習題

1. 氫原子的電離能為 1312 kJ/mol，H₂⁺分子離子的鍵解離能為 256 kJ/mol。H₂⁺分子離子的重疊積分S由表示式S = (1 + R/a₀ + R²/3a₀²)exp(-R/a₀)給出，其中R為鍵長（1.06 Å），a₀為玻爾半徑，0.529 Å。H₂⁺的α和β（單位為 kJ/mol）的值是多少？

2. 使用H₂的分子軌道能級圖比較H₂⁺和H₂^-的鍵序。H₂^-離子的鍵解離能為 156 kJ/mol，而H₂⁺的鍵解離能為 256 kJ/mol。這是你根據鍵序預期的嗎？為什麼H₂^-的鍵解離能比H₂⁺的鍵解離能低得多？

3. HHe的鍵序是多少？為什麼這種化合物從未被分離出來？

4. 你預計Be₂⁺分子離子在氣相中會穩定嗎？總鍵序是多少，有幾個淨σ鍵和π鍵？

5. 對氣相6族二氟化物（XF₂）分子中F-X-F鍵角的以下週期性趨勢給出合理的解釋。（提示 - 它與s和p軌道能量的趨勢有關；見第1章，第1.2節）

化合物	F-M-F角度（度）
OF2	103
SF2	99
SeF2	97
TeF2	95

6. 氧的最穩定同素異形體是O₂，但類似的硫分子（S₂）相對於S₈同素異形體不穩定。解釋原因。

7. 使用分子軌道理論，說明為什麼H₃分子具有三角形（或彎曲）而不是線性形狀。

8. 使用MO理論確定以下分子的鍵序和未成對電子的數量：（a）O₂^-，（b）O₂⁺，（c）NO⁺，和（d）NO^-。使用鮑林公式和中性NO分子中的鍵長（1.151 Å）估計NO^-和NO⁺中的鍵長。

10. 比較MO理論和價鍵理論在描述以下分子的成鍵方面的結果：（a）CN^-和（b）中性CN。根據MO理論，在第二週期雙原子分子中，鍵序可能大於3嗎？

11. 中性BN分子僅在氣相中穩定。該分子聚合形成固態氮化硼，它以石墨狀和超硬金剛石狀形式存在。繪製BN分子的分子軌道能級圖。確定σ和π鍵序以及未成對電子的數量。

12. 氣相BN分子的鍵長為 1.44 Å。使用鮑林公式和你在問題11中確定的鍵序，計算氨硼烷 (H3B-NH3) 中的 B-N 鍵序，其中鍵長為 1.658 Å。你的計算結果與價鍵理論預期的 B-N 鍵序一致嗎？

13. 繪製線性[FHF]^-離子的MO圖。你只需要關注邊界軌道，即H 1s 和兩個沿成鍵（z）軸的 F sp_z雜化軌道。HF 鍵的順序是什麼？原子上的形式電荷是多少？

14. 環辛四烯 (cot) 分子（想象一個有四個雙鍵的停止標誌）具有褶皺的環狀結構。然而在U(cot)₂中，鈾的氧化態為4+，cot配體的形式電荷為2-，8元環是平面的。為什麼cot^2-是平面的？

15. 繪製以下原子軌道，包括不同相位的不同陰影、x、y和z軸以及軌道的名稱。按能量順序對它們進行編號，能量最低的軌道為#1，能量增加的軌道為數字增加。不需要剖檢視，只繪製表面。3d_x2-y2，2p_x，3d_z2，3s，3p_y，3d_xz，3d_yz。

16. 繪製以下分子軌道，包括不同相位的不同陰影以及軌道的名稱。按能量順序對它們進行編號，能量最低的軌道為#1，能量增加的軌道為數字增加。1σ_2p軌道，2個不同的π*_2p軌道，1σ*_2s軌道，1σ_1s軌道，1σ*_2p 軌道。

17. 繪製一個沃爾什圖，展示MO圖如何從線性 H-X-H 分子（其中 X 是第二週期元素，如 Be、B、C、N 或 O）轉變為彎曲的分子。使用該圖預測H₂O分子是線性的還是彎曲的。總鍵序是否與H₂O的價鍵圖一致？