無機化學導論/化學鍵概述

分子(和擴充套件的固體)是由形成化學鍵的原子構成的。鍵合理論試圖解釋為什麼分子和固體會形成,它們的結構是什麼,為什麼有些比其他更穩定,以及它們如何反應。正如我們將在第二章中瞭解到的,量子力學透過分子軌道 (MO) 理論為我們提供了化學鍵合最真實的圖景。然而,MO 鍵合描述在概念上很困難,在數學上也很複雜。本章將回顧一些不太嚴格(但仍然有用)的模型,例如路易斯點結構和價層電子對互斥 (VSEPR) 理論。當與透過軌道雜化和共振概念進行定性量子力學描述結合時,這些簡單模型可以幫助我們瞭解無機分子的結構、穩定性和反應。
化學鍵理論有著悠久的歷史,可以追溯到古希臘原子論者德謨克利特、留基波斯和伊壁鳩魯學派。他們假設存在著在虛空中運動的不變原子,並將物質的物理性質視為由原子的種類和形狀造成的。羅馬詩人盧克萊修(約公元前 99 年 - 約公元前 50 年)在他的史詩《論物之本性》中,借鑑了伊壁鳩魯學派的信仰,以以下方式描述了一些原子和化學鍵:
在我們看來堅硬而凝結的東西
一定是原子在彼此之間互相勾連,
緊密地結合在一起,就好像
透過樹枝狀的原子——其中最主要的
是金剛石,蔑視一切打擊
堅固的燧石和堅硬的鐵
以及黃銅棒,它們在鎖中難以移動,
會發出摩擦和尖叫聲。但是,液體是什麼,形成
流體物質,它們確實必須
由更光滑和圓形的元素組成——因為
它們的球體分別不會粘在一起。
盧克萊修的詩歌讀起來很愉快,考慮到當時可用的工具,它對微觀世界有一些非凡的見解。然而,現代分析方法表明他的關於鉤子和球體的想法是錯誤的。我們將根據現代化學理論,重新審視盧克萊修提到的物質(金剛石、矽酸鹽、鐵、黃銅和水)中化學鍵的性質,以瞭解為什麼它們具有它們所具有的特殊性質。
第一章學習目標
- 能夠繪製路易斯點結構,分配形式電荷,預測分子幾何形狀(包括鍵角),並計算分子的鍵級,包括超價分子和離子。
- 使用非鍵共振描述超價分子。
- 理解並闡明如何透過實驗驗證分子結構和鍵合的預測。
- 學習從 s 和 p 原子軌道構建雜化軌道。
- 使用等電子原理設計新的分子和固體。
- 使用鍵極性引數合理化鍵強度和化學反應性。
- 相互關聯鍵長和鍵強度。

原子和分子
原子論,因為它被亞里士多德所摒棄,在科學話語中沉睡了很長時間,直到 17 世紀被伽利略、笛卡爾和伽桑狄重新考慮。道爾頓在 1808 年基於他觀察到的氫和氧等元素以特定比例結合(定比定律)假設了現代原子理論,但原子理論在整個 19 世紀的大部分時間裡仍然存在爭議。湯姆森、盧瑟福、玻爾以及 20 世紀初的其他人在建立了物質確實是包含重核和輕電子的原子組成,以及原子可以存在於可以解釋為電子激發到不同能級的激發態時。然而,原子理論並沒有為分子中原子的鍵合態提供一個現成的解釋。
1916 年,在現代量子理論充分描述原子軌道的形狀之前十多年,路易斯基於經驗觀察的化合價規則,即原子在分子中的結合比例,提出了八隅律。[1] 事後看來,這個理論可以根據主族元素的觀察結果進行合理化,即主族原子可以使用它們的四個價電子軌道(s、px、py 和 pz)來容納多達八個電子,其中一些或全部電子可能與其他原子共享。在路易斯的模型中,原子的價電子位於立方體的角上,立方體可以共享邊或面來完成它們的八隅體。路易斯開發了一種基於點的簡寫符號來表示這些結構,這些點代表價電子,如圖 1.1.1 所示。原子之間共享的一對電子構成一個化學鍵,也可以用連線原子的線來表示。原子之間共享的四個電子,用兩條線表示,是一個雙鍵,依此類推。任何不參與鍵合的電子對都形成“孤對”,只屬於一個原子,因此不參與鍵合。
路易斯圖在簡單性方面功能強大。它可以很容易地用來合理化或預測原子的結合比例,對分子的合理和不合理的結構進行排序(包括大型分子),以及合理化許多分子的酸鹼性質。重要的是要記住,該模型建立在對原子不穩定的、量子力學前描述的基礎上,因此使用它,我們會犯錯誤。然而,看看我們可以用路易斯模型走多遠還是很有用的。
構建分子的八隅體價鍵圖
我們可以使用N-V 方法為任何分子構建一個八隅體圖:
- 圍繞所有原子形成獨立八隅體所需的電子數 = N
- (N = 8 對於非 H 原子,N = 2 對於 H)
- 價電子數 = V(使用族號加起來;不要忘記在離子上的電荷中加或減)
- 共享電子數 = S = N-V;因此鍵數 = S/2
- 在其他所有地方填入孤對以完成八隅體
示例:硝酸根陰離子 NO3-
- N = 4 個原子 x 8 個電子 = 32
- V = 5 + 6 + 6 + 6 + 1 = 24 (N + O + O + O + 電荷)
- S = 32-24 = 8 個共享電子 = 4 個鍵
- 孤對數由差值獲得:(V-S)/2 = (24-8)/2 = 8
- 現在繪製分子,從四個鍵開始,然後新增八個孤對以完成八隅體
- 計算硝酸根陰離子中每個原子周圍的共享電子和非共享電子,你會發現所有原子都處於八隅體狀態,並且價電子總數 (V) 為 24。如果你按照上述規則進行 N-V 計算,你應該始終得到一個八隅體結構。

形式電荷分佈是透過將共享(鍵合)電子平均分配給原子來確定的。因此,單鍵 O 原子各自擁有 7 個電子,因為 O 位於第 6 族,所以它們的正式電荷為 -1。雙鍵 O 的正式電荷為零。N 原子的正式電荷為 +1,因為它“擁有” 4 個價電子,並且位於第 5 族。
請注意,形式電荷與氧化數(或氧化態)不同。在硝酸根陰離子中,氮的氧化態為 +5,氧的氧化態為 -2。形式電荷通常更接近原子上的“真實”電荷(例如,透過X 射線光電子能譜測量)。氧化態是跟蹤氧化還原反應的有用記賬工具,我們將在第四章中討論。與氧化態一樣,分子或離子中原子上的形式電荷必須加起來等於其總電荷。
我們可以類似地繪製氨的 Lewis 結構,如下所示
當我們將共享電子平均分配給原子時,我們看到 N 原子有五個電子,每個 H 原子有一個電子。這些與它們的族號相同,因此,氨分子中的所有形式電荷都為零。
下面顯示了路易斯酸鹼加合物 NH3BF3、水合氫離子 H3O+ 和硫酸根陰離子 SO42- 的八隅體結構。在這種情況下(以及我們繪製的許多路易斯結構中),我們省略了周圍原子周圍的隱含孤對。嘗試使用 N-V 方法計算這些分子中每個分子的鍵數,並補充那些沒有明確繪製的孤對。
在可能存在多個價鍵結構的情況下,我們可以使用形式電荷來判斷哪個結構應該更穩定或更不穩定。規則如下:
- 穩定結構中原子上的形式電荷最小化,零是最理想的情況。
- 負形式電荷應放在最具電負性的原子(s) 上。
- 正形式電荷應放在最不具電負性的原子(s) 上。
- 在分子中將類似電荷 (++ 或 --) 放在相鄰原子上的做法是不利的。
下面顯示了這些規則在 BF3 和 ONF 的替代結構中的示例。


海洋之外的生命的存在歸功於平流層中臭氧 (O3) 的存在。臭氧吸收太陽光譜中的紫外線,否則會對 DNA 和其他生物分子造成災難性的損害。由於臭氧是由 O2 光化學產生的,而 O2 本身是由光合作用產生的,因此遙遠行星大氣中臭氧的光譜特徵是尋找地外生命的一種可能方法。 
蘇珊·所羅門 發現了臭氧被氯氟烴(氟利昂)分解的異質催化機制,形成了南極臭氧洞。她的工作為《聯合國蒙特利爾議定書》奠定了基礎,該議定書是一項國際協議,透過規範有害化學物質來保護臭氧層。
在 BF3 的情況下,左側的結構是非八隅體的,因為 B 的價電子層中只有六個電子(三個鍵)。這種結構被稱為電子缺陷。可以繪製八隅體結構(右側),但它在 F 上放置了一個正形式電荷,F 是分子中最具電負性的原子。因此,兩種結構都不是完全“快樂”的,但形式電荷規則告訴我們,左側的電子缺陷結構更穩定。BF3 的電子缺陷使其成為一種強大的路易斯酸。
在 ONF 的情況下,左側的結構有兩個原因不利。首先,它在 F 上放置了一個正形式電荷,F 是最具電負性的原子。其次,還有另一種可能的結構(右側),該結構的形式電荷為零,這比具有非零電荷的結構更可取。這意味著右側的結構(在 N 和 O 之間具有雙鍵)更合理。
共振結構
臭氧 (O3) 分子具有兩個等效的八隅體結構,如下所示:
在這兩種情況下,路易斯點圖表明分子中存在三種氧原子,其形式電荷分別為 +1、0 和 -1。這些結構還表明臭氧應該有一個單鍵和一個雙鍵。然而,透過實驗(透過 電子衍射),我們發現該分子是對稱的,兩個 O-O 鍵長相同。真實的(瞬時)結構是兩種形式的平均值,如下所示。在該分子的經典路易斯圖中,我們可以透過觀察電子比原子核輕幾千倍,因此在分子振動的時標上移動速度非常快來合理化共振。因此,在氧原子調整其位置所需的時間內,電子可以來回移動多次。在量子力學 MO 圖(第二章)中,我們將看到共振涉及完全在分子中的原子之間離域的電子。我們用雙箭頭表示共振結構,以表示路易斯結構之間唯一的區別是電子的分佈。
在臭氧的瞬時結構中,形式 (-) 電荷在兩個末端氧原子之間共享,因此每個氧原子的形式電荷為 -1/2。O-O 鍵是單鍵和雙鍵的平均值,即每個 O-O 鍵級為 1.5。

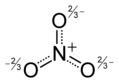
類似地,硝酸根陰離子具有三個共振結構,並且透過實驗(透過硝酸鹽的 X 射線晶體學)我們發現離子中所有的 N-O 鍵都是相同的。在這種情況下,在平均結構中,每個 O 原子的形式電荷為 -2/3,N-O 鍵級為 4/3 (=1.33...)。

不等價的共振結構
共振規則也適用於不等價結構,這些結構通常彼此具有不同的能量。在這種情況下,分子的結構代表低能量結構的加權平均值。一個很好的例子是氰酸根離子 OCN-。我們可以為該分子寫出三個不等價的八隅體結構:
前兩個是合理的共振結構,儘管我們懷疑左側的結構是最好的,因為它將負形式電荷放在最具電負性的原子。最後一個結構顯然是一個糟糕的共振結構,因為形式電荷很高,並且氧原子帶正電荷。因此,真實的結構是前兩個結構的加權平均值。
無鍵共振
一種有趣且有用的不等價共振結構是在兩個原子之間具有零鍵級。這種無鍵共振的概念對於理解許多含鹵素和含氫化合物的鍵合非常重要。該概念在下面針對通用分子 X-Y-Z 進行說明,其中 Z 可以是諸如 F 之類的電負性鹵素原子。透過將鍵合電子從 Y-Z 鍵移動到 Z 原子上,並將孤對從 X 移動到 X-Y 鍵中,我們生成了右側所示的共振結構,其中所有原子都保持八隅體,但 Y 和 Z 之間沒有鍵。

重要的是要認識到在這個例子中,無鍵形式只是一個共振結構,因此 Z 原子仍然與 Y 鍵合。如果這兩個共振結構在這個例子中具有相同的能量,我們預計 X-Y 鍵級為 1.5,Y-Z 鍵級為 0.5。因此,Y-Z 鍵應該比鍵級為一的化合物中的鍵長,並且應該相對容易斷裂 Y-Z 鍵。
下面顯示了無鍵共振的一些分子例子。在 ONF3 分子中,N-F 鍵比 NF3 中的 N-F 鍵長得多,在 NF3 中,鍵級為 1。這可以透過右側顯示的無鍵共振形式來解釋。類似地,在透過將 BH3 與 CO 相結合形成的路易斯酸鹼加合物中,我們可以使用將部分正電荷放在 H 原子上的無鍵共振形式來解釋長的 B-H 鍵。

無鍵共振通常用於為所謂的超價化合物提供八隅體鍵合圖,這些化合物似乎在中心原子的鍵合殼層中具有超過 8 個價電子。例如,我們可以考慮三碘離子 I3- 的兩種不同的價鍵結構,該離子是透過 I- 與 I2 在水中反應形成的:


在這個結構中,中心碘原子在其價電子層中具有 10 個電子,違反了八隅體規則。拉曼光譜表明三碘離子的 I-I 鍵比 I2 中的 I-I 單鍵弱,這表明這種圖不是對鍵合的準確描述。可以使用無鍵共振結構來獲得 I3- 的更好表示,如下所示。我們將看到這種圖與第二章中 I3- 的 MO 描述是一致的。
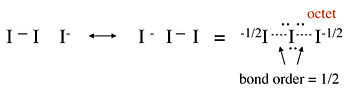

我們可以為 XeF2 分子繪製類似的圖,該分子具有與 I3- 相同數量的價電子。這種圖與 XPS 資料一致,XPS 資料顯示 F 原子帶部分負電荷,以及振動光譜,振動光譜表明 XeF2 中的 Xe-F 鍵比單鍵陽離子 Xe-F+ 中的 Xe-F 鍵弱。

其他眾所周知的超價化合物包括 PF5、P(CH3)5 和 SF6,以及含氧酸,如 H2SO4 和 HClO4。這些分子的超價結構通常被畫出來,並解釋說中心原子的 d 軌道參與了成鍵,形成 5 配位和 6 配位分子分別的 dsp3 和 d2sp3 雜化軌道。然而,真實的分子軌道計算表明,磷和硫的 3d 軌道能量太高,無法顯著參與 PF5 和 SF6 中的成鍵。對於這些分子,我們可以使用無鍵共振來構建合理的八隅體結構,預測中心原子和 F 之間的極性鍵。


在其他情況下,例如 P(CH3)5,八隅體結構不合理,因為它表明 P 和 C 之間存在極性鍵,且 C 帶有部分負電荷。此外,在含氧酸,例如 H2SO4 和 HClO4 的情況下,X 射線晶體學資料表明,與氫原子不鍵合的氧原子上的 S-O 和 Cl-O 鍵更短,這與超價結構更一致。

超價和八隅體規則是否真正有效地描述了這些化合物中的成鍵問題,已經在許多計算研究中進行了探討,這些研究使用越來越精確的量子力學計算來確定與中心原子相關的電子數。在 2002 年的一項研究中,Gillespie 和 Silvi[4] 發現,對於具有正電性配體的化合物,例如 P(CH3)5,價層電子數大於 8,而對於像 PF5 這樣的化合物,價層電子數小於 8。他們得出結論,這些價層電子殼層電子數主要取決於中心原子及其配體的配位數和電負性,並且超價分子和非超價分子(路易斯八隅體)之間的成鍵沒有本質區別。這提醒我們,八隅體規則不是自然規律,而是一個在一定範圍內有效的經驗規則。

等電子原理
在使用 N-V 方法計算分子的八隅體結構時,我們只需要知道原子數和電子數,而不需要知道原子的具體種類。這意味著對於包含以下條件的任何分子或離子,我們都會得到相同的答案(以及相同的八隅體和共振結構):(a) 具有相同數量的非氫原子,以及 (b) 具有相同的總價電子數。這類分子被稱為等電子分子。這是一個強有力的結論,因為一旦我們確定了一個分子的電子結構,我們就可以為所有其他等電子分子寫出相同的解。例如,我們在上面已經注意到,I3- 和 XeF2 都有 22 個價電子,它們具有相同的價鍵結構。我們還可以預期等電子分子具有相同的形狀,並且通常具有相似的物理性質。
以下四個分子和離子都包含三個非氫原子和 16 個價電子。它們都是具有兩個雙鍵的直線形分子。以下所示的四個分子和離子都包含四個非氫原子和 24 個價電子。這四個分子具有三角形平面結構。雖然 BF3 是這個等電子系列的成員,但我們不將其寫成包含 B=F 雙鍵的共振形式,因為這會導致 F 上帶有正形式電荷。
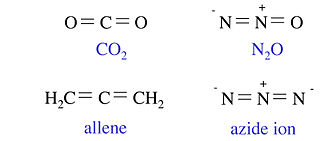

類似地,我們可以證明 CH4、NH3、NH4+、H2O、H3O+、HF、F- 和 OH- 都與一個非 H 原子和八個價電子等電子。在下一節中,我們將看到這導致了這些分子幾乎相同的電子形狀。

等電子固體。等電子原理不僅適用於分子,也適用於擴充套件的固體。一組具有技術重要性的等電子固體是 p 區半導體。第 14 族元素 Si 是最廣泛使用的電子半導體,但正如我們將在後面討論的那樣,它不是一個好的發光體。用於雷射、高效率照明和顯示技術的 LED(發光二極體)是由與 Si 和 Ge 等電子的化合物製成的,特別是 GaAs、GaP、AlAs 和 GaN(每個原子都包含四個價電子)。CdTe 和 CuIn1-xGaxSe2 (CIGS) 是很有前途的太陽能電池材料,它們也具有相同數量的價電子。與 Si 和 Ge 一樣,這些化合物在固態下具有四面體鍵合結構,並吸收了大部分太陽光譜的光,正如我們將在第 8 章和第 10 章中更詳細地討論的那樣。
等電子原理也是材料研究中一個強大的工具,因為它為尋找具有相似甚至改進性質的新材料提供了指導。例如,發現可以用 CsSnI3[5] 製造 8.5% 效率的薄層太陽能電池,促使人們探索許多具有相同鈣鈦礦晶體結構的等電子 ABX3 化合物。最近,基於該結構家族中光吸收劑的薄膜太陽能電池(MA)PbI3-xClx 和 FAxMA1−xPbBryI3−y(MA+ = 甲胺,CH3NH3+;FA+ = 甲醯胺,HC(NH2)2+)被報道,其效率高達 22%。[6][7][8]
1.2 分子的形狀(VSEPR 理論)和軌道雜化
[edit | edit source]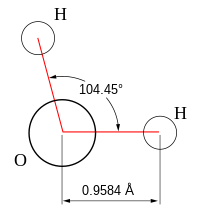
價層電子對互斥理論 (VSEPR) 是一種簡單且有效的方法,可以預測和解釋分子的形狀。該理論基於最小化電子對之間的靜電排斥的概念,正如 Sidgwick 和 Powell 在 1940 年首次提出的那樣,[9] 然後由 Gillespie 和 Nyholm 在 1957 年推廣,[10] 並在此後的 50 多年中被廣泛應用。 [11]
為了使用 VSEPR 模型,首先需要使用路易斯點圖來確定中心原子周圍的孤對數和成鍵域數。因為 VSEPR 將所有成鍵域視為相等(即,單鍵、雙鍵和半鍵都算作一個電子域),所以可以使用八隅體結構或超價結構,只要孤對數(在兩種結構中應該相同)被正確計算即可。例如,在上述 I3- 離子的超價結構或八隅體結構中,中心 I 原子上都有三個孤對和兩個成鍵域。然後,我們按照以下步驟來獲得電子幾何形狀
- 確定分子中中心原子的孤對數,並加上成鍵原子的數量(也稱為成鍵域)。
- 這個數字(空間數)透過最小化排斥來定義分子的電子形狀。例如,空間數為 3 會形成一個三角形平面電子形狀。
- 電子域之間的角度主要由電子幾何形狀決定(例如,空間數為 4 時為 109.5°,這意味著電子形狀為四面體)。
- 這些角度透過排斥力的等級進行調整:(孤對 - 孤對)>(孤對 - 鍵)>(鍵 - 鍵)。
分子幾何形狀從電子幾何形狀推斷而來,將孤對視為存在但不可見。確定分子結構最常用的方法——X 射線衍射、中子衍射和電子衍射——很難看到孤對,但它們可以準確地確定原子間鍵長和鍵角。
下表列出了空間數為 2 到 9 的電子形狀和分子形狀示例。我們最常關注的是空間數為 2 到 6 的分子。
| 成鍵電子對 | 孤對 | 電子域(空間數) | 形狀 | 理想鍵角(示例中的鍵角) | 示例 | 影像 |
|---|---|---|---|---|---|---|
2
|
0
|
2
|
180°
|
|||
3
|
0
|
3
|
120°
|
|||
2
|
1
|
3
|
120°(119°)
|
|||
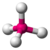
4
|
0
|
4
|
109.5°
|
|||
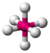
3
|
1
|
4
|
109.5°(107°)
|
|||
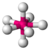
2
|
2
|
4
|
109.5°(104.5°)
|
|||
5
|
0
|
5
|
90°、120°、180°
|
|||
4
|
1
|
5
|
180°、120°、90°(173.1°、101.6°)
|
|||
3
|
2
|
5
|
90°、180°(87.5°、< 180°)
|
|||
2
|
3
|
5
|
180°
|
|||
6
|
0
|
6
|
90°、180°
|
|||
5
|
1
|
6
|
90°(84.8°)、180°
|
|||
4
|
2
|
6
|
90°、180°
|
|||
7
|
0
|
7
|
90°、72°、180°
|
|||
6
|
1
|
7
|
72°、90°、144°
|
XeOF5−
|
||
5
|
2
|
7
|
72°、144°
|
|||
8
|
0
|
8
|
||||
9
|
0
|
9
|
從表中我們可以看到,一些作為示例的分子具有偏離理想電子幾何形狀的鍵角。例如,氨分子中的 H-N-H 鍵角為 107°,水分子中的 H-O-H 鍵角為 104.5°。我們可以用上面的最後一條規則來解釋這一點。氨中的孤對電子對 N-H 鍵中的電子產生更大的排斥作用,比鍵之間相互排斥更大。在水分子中,由於存在兩個孤對電子,這種孤對電子排斥作用會產生更大的空間影響。類似地,在“蹺蹺板”分子 SF4 中,軸向 F-S-F 鍵角由於分子中孤對電子的排斥作用而略小於 180°。
幾何異構體
對於表中的一些分子,我們注意到,存在多種可能的形狀可以滿足 VSEPR 規則。例如,XeF2 分子具有 5 的空間數和三角雙錐幾何形狀。存在三種可能的立體異構體:一種是 F 原子佔據軸向位置,導致形成線性分子,一種是 F 原子佔據一個赤道位置和一個軸向位置(導致 90° 的鍵角),另一種是 F 原子都位於赤道位置,F-Xe-F 鍵角為 120°。

XeF2 的觀察到的幾何形狀是線性的,這可以透過考慮用於形成軸向和赤道位置的鍵(或孤對電子)的軌道來解釋。存在四個可用的軌道,s、px、py 和 pz。如果我們選擇 z 軸作為軸向方向,我們可以看到 px 和 py 軌道位於赤道平面。我們假設球形的 s 軌道被分子中的五個電子域平均共享,兩個軸向鍵共享 pz 軌道,三個赤道鍵共享 px 和 py 軌道。然後我們可以計算軸向和赤道 F 原子的鍵序如下
軸向:1/5 s + 1/2 pz = 0.7 鍵(形式電荷 = -0.3)
赤道:1/5 s + 1/3 px + 1/3 py = 0.867 鍵(形式電荷 = -0.133)
由於氟比孤對電子更具電負性,它更喜歡軸向位置,在那裡它將具有更負的形式電荷。一般來說,根據這種推理,孤對電子和像 CH3 這樣的正電性配體在三角雙錐幾何形狀中總是更喜歡赤道位置。像 F 這樣的負電性配體總是會佔據軸向位置。
在 BrF4- 陰離子(與表中的 XeF4 等電子)的情況下,電子幾何形狀是八面體形的,存在兩種可能的異構體,其中兩個孤對電子彼此為順式或反式。在這種情況下,孤對電子-孤對電子排斥作用占主導地位,我們獲得了孤對電子的反式排列,從而形成了平面正方形分子幾何形狀。

軌道雜化
觀察到上述各種電子形狀的分子,乍一看,與我們對原子軌道的認識相矛盾。對於像氧這樣的原子,我們知道 2s 軌道是球形的,而 2px、2py 和 2pz 軌道是啞鈴形的,並且沿著笛卡爾座標軸指向。水分子包含兩個與氧原子相連的氫原子,它們並非以 90° 的角度相連,而是以 104.5° 的角度相連。考慮到原子軌道的相對取向,我們如何得到 104.5°、120° 等電子域之間的角度?為了理解這一點,我們需要了解一些關於原子和分子中電子的量子力學知識。
原子軌道 ψ 代表薛定諤方程的解,
這裡 E 是軌道中電子的能量,而 是哈密頓算符。
與經典力學類似,哈密頓算符通常表示為對應於系統的算符的動能和勢能之和,形式為
其中 是勢能,並且
是動能算符,其中m是粒子的質量,動量算符為
- 其中
這裡 是 h/2π,其中 h 是普朗克常數,拉普拉斯算符 ∇2 為
雖然這並非經典力學中哈密頓量的技術定義,但它是它在量子力學中最常見的形式。將這些結合在一起就會得到薛定諤方程中使用的熟悉形式
對於類氫(單電子)原子,薛定諤方程可以寫成
其中Z為核電荷,e為電子電荷,r為電子的位置。等式右側的徑向勢項是由於庫侖相互作用,即原子核和電子之間的靜電吸引,其中ε0是介電常數(自由空間的介電常數),並且
是質量為mn的原子核和質量為me的電子的二體約化質量。近似地,µ ≈ me。

這就是埃爾溫·薛定諤在 1926 年著名的推匯出的方程,用於求解類氫原子中 s、p、d 和 f 原子軌道的能量和形狀。對於物理學和化學來說,這是一個巨大的概念飛躍,因為它不僅解釋了氫原子的量子化能級,而且還為八隅體規則和元素在週期表中的排列提供了理論基礎。
如果我們將適當的勢能函式 V(r,t) 代入哈密頓量,薛定諤方程可以用來描述比氫原子更復雜的化學體系(例如多電子原子、分子、無限晶體以及這些體系的動力學)。在這些情況下,數學變得更加複雜,必須用數值方法求解方程,所以為了我們的目的,我們將堅持最簡單的情況:時間不變、單電子、類氫原子。

在不深入討論薛定諤方程的太多細節的情況下,我們可以指出它的一些最重要的性質
- 該方程源於這樣一個事實:總能量 (E) 是動能 (KE) 和勢能 (PE) 的總和。這三個量在數學上用方程中的算符表示。
- 在方程的左側,總能量算符 (E) 是一個標量,它乘以波函式 ψ。ψ 是空間座標 (x,y,z) 的函式,它與電子在空間中該點的機率相關。
- 方程右側的第一項表示動能 (KE)。動能算符與 ∇2(拉普拉斯算符)成正比,它對 ψ 進行二階導數(關於三個空間座標)。因此,薛定諤方程是一個微分方程。
- 方程右側的第二項表示庫侖勢 (PE),即帶正電的原子核和帶負電的電子之間的吸引力。
- 薛定諤方程的解是一組能量 E(它們是標量)和波函式(也稱為原子軌道)ψ,它們是空間座標的函式。您有時會看到能量被稱為特徵值,軌道被稱為特徵函式,因為在數學上,薛定諤方程是一個特徵函式-特徵值方程。雖然 ψ 是座標的函式,但 E 不是。因此,處於 2pz 軌道的電子無論在空間中的什麼位置,其總能量 E (= PE + KE) 都是相同的。
- 這些 E 值及其相關的波函式 ψ 是根據它們的量子數 n, l, 和 ml 進行分類的。也就是說,微分方程有許多解,並且每個解 (ψ(xyz) 和 E) 都有一組唯一的量子數。一些軌道集是簡併的,這意味著它們具有相同的能量(例如,2px、2py 和 2pz)。
- 薛定諤方程的解 ψ(xyz)(例如 1s、2s、2px、2py 和 2pz 軌道)代表在空間中特定點 (x,y,z) 找到電子的機率幅度。機率幅度可以是+ 號或 - 號。我們通常用 2p 軌道的兩個葉片上的陰影或 + 和 - 符號來表示不同的符號。
- 機率振幅的平方,ψ2,始終為正數,表示在空間中 x,y,z 點找到電子的**機率**。因為找到電子的總機率為 1,所以波函式必須進行**歸一化**,使得 ψ2 在空間座標(從 -∞ 到 +∞)上的積分等於 1。
- 薛定諤方程的解是**正交**的,這意味著任意兩個解的乘積(在整個空間上積分)都為零。例如,2s 和 2px 軌道的乘積,在空間座標從 -∞ 到 +∞ 上積分,結果為零。
軌道雜化涉及對作為薛定諤方程解的原子軌道進行線性組合。從數學上來說,這是透過認識到薛定諤方程是一個線性微分方程來證明的。因此,薛定諤方程解的任何求和也是一個有效的解。然而,我們仍然需要限制條件,即我們的雜化軌道必須是**正交**的並且是**歸一化**的。
軌道雜化的規則
對於**sp 雜化**,例如 BeF2 或 CO2 分子,我們對 2s 和 2pz 軌道(將 z 作為 Be-F 鍵的軸)進行兩個線性組合
這裡我們只是將 2s 和 2pz 軌道加減起來;我們將證明這兩個軌道都是歸一化的(即 ∫ψ12dτ = ∫ψ22dτ = 1)並且是正交的(即 ∫ψ1ψ2dτ = 0)作為練習留給感興趣的讀者。
這在物理上意味著什麼在下圖中解釋。透過結合 2s 和 2pz 軌道,我們創造了兩個沿 z 軸指向的具有較大葉瓣(高電子機率)的新軌道。這兩個軌道是簡併的,並且能量介於 2s 和 2pz 軌道之間。

對於一個孤立的 Be 原子,它有兩個價電子,最低能量狀態將有兩個電子在 2s 軌道上自旋配對。然而,這些電子將無法用於成鍵。透過將這些電子**提升**到簡併的 2spz 雜化軌道,它們變得未配對,並準備與 BeF2 中的 F 原子成鍵。如果**成鍵能量**(在提升狀態下)超過了提升能量,則這種情況將會發生。**總成鍵能量**,即 Be 原子在其基態與兩個 F 原子結合時釋放的能量,是成鍵能量和提升能量之間的差值。
我們同樣可以從一個 2s 和兩個 2p 原子軌道構建**sp2 雜化軌道**(例如,對於 BF3 分子或 NO3- 陰離子)。以分子平面為 xy 平面,我們得到了三個雜化軌道,它們彼此之間的夾角為 120°。三個雜化軌道分別是

這些軌道再次是簡併的,它們的能量是 2s、2px 和 2py 原子軌道能量的加權平均值。
最後,為了形成 sp3 雜化軌道,例如在 CH4、H2O 等分子中,我們將所有四個 原子軌道組合起來形成四個簡併的雜化軌道


sp3 雜化軌道 的葉瓣指向四面體 (或立方體的交替角),這與 CH4 中的四面體鍵角以及 NH3 和 H2O 中接近四面體的角度相一致。同樣,我們可以證明,我們可以透過構造 sp 和 sp2 雜化來構建三角雙錐電子形狀,以及從三組 sp 雜化構建八面體幾何形狀。由此產生的影像是,原子軌道可以根據最能使電子對排斥最小化的形狀進行雜化。

然而,有趣的是,PH3、H2S 和 H2Se 中的鍵角接近 90°,這表明 P、S 和 Se 主要在這些分子中使用它們的 p 軌道與 H 形成鍵。這與週期表中 s 和 p 軌道之間的能量差在下降過程中大致保持不變這一事實一致,但鍵能隨著價電子離原子核越來越遠而減小。因此,在週期表中第三、第四和第五行的元素的化合物中,使用 s-p 軌道雜化在成鍵中的趨勢下降。對於這些較重的元素,鍵能不足以抵消將 s 電子提升到 s-p 雜化軌道所需的能量。

萊納斯·鮑林 在 1932 年提出了電負性的概念來解釋具有極性鍵的分子額外的穩定性。[12] 原子的電負性,用希臘字母 χ 表示,可以定義為原子在化學鍵中吸引電子的趨勢。在鮑林標度上,兩個原子 A 和 B 之間的電負性差被定義為解離能 Ed 的 A-A、B-B 和 A-B 鍵
其中能量以電子伏特表示。
這個定義,雖然直接與化學鍵的強度相關,但需要來自許多化合物的熱化學輸入資料,其中一些資料在當時不可用。Mulliken[13][14] 以及後來的 Pearson[15] 開發了一個基於自由 A 和 B 原子的電子親和能和電離能平均值的電負性標度,他們將此標度與熱化學資料和鮑林標度相關聯。
在鮑林標度上,電負性最小的元素是鹼金屬 (χ = 0.7-1.0),電負性最大的元素是氧 (3.5) 和氟 (4.0),位於週期表的上右側。碳和氫的電負性介於兩者之間 (分別為 2.6 和 2.2,以鮑林標度為單位)。總體趨勢 (見下表) 是電負性在週期表中向上和向右移動時增加。這種行為有一些有趣的例外,最值得注意的是在過渡系元素底部出現了兩個高電負性島,在鎢 (χ = 2.4) 和金 (χ = 2.5) 處達到峰值。第一個可以解釋為 Mo 和 W 等元素的金屬 - 金屬鍵能非常高,它們可以在成鍵中使用所有六個價電子,正如我們在第 6 章中討論的那樣。然而,第二個發生在 Pt 和 Au 等鍵合較弱的貴金屬中,這會導致它們在活性系列中的位置較低,[16] 以及它們作為催化劑的非凡性質。

鍵的極性由電負性差決定。作為指南,我們將鍵定義為
- 離子鍵 如果 Δχ > 2.0
- 極性鍵 如果 2.0 > Δχ > 0.5
- 非極性鍵 如果 0.5 > Δχ
鍵的極性有助於我們理解分子之間的非共價力,例如氫鍵和偶極 - 偶極相互作用。它還有助於我們解釋分子的反應性。例如,Si-H 鍵 (χSi = 1.8, χH = 2.1) 比 C-H 鍵 (χC = 2.5, χH = 2.1) 更像氫化物。因此,矽烷與酸反應生成 H2,而膦 (χP = 2.1) 和烴則不會。同樣,親電取代反應在 Si-H 和 P-H 化合物上比在 C-H 化合物上更容易發生。
化學鍵的強度也與鍵長相關,鍵越長,由於軌道重疊較弱,鍵越弱。鮑林提出了一個將鍵長與鍵強度相關聯的經驗公式。對於給定的一對原子(例如,兩個碳原子)
- D(n) = D(1) - 0.6 log10(n)
其中 D(n) 代表以 Å 為單位的鍵長,n 是鍵級。在這種情況下,D(1) 將是 C-C 單鍵的長度,我們可以從烷烴中的平均鍵長 (1.54 Å) 獲得。使用這個公式,我們可以預測乙烯 (C=C 雙鍵) 和乙炔 (C≡C 三鍵) 中的鍵長應該分別為 1.36 和 1.25 Å,這與實驗值 1.33 和 1.20 Å 接近。在相關形式中,鮑林公式可用於計算當單鍵長度 D(1) 不可用時的鍵長
- D(n) = D(m) - 0.6 log10(n/m)
這裡 n 和 m 代表同一類原子之間的兩個不同的鍵級。這告訴我們,例如,三鍵和雙鍵之間的長度差,D(2)-D(3),應該為 - 0.6 log10(2/3) = 0.11 Å。

一些鍵長和鍵能是異常的。例如,F2 中的 F-F 鍵長為 1.43 Å,比 F 原子共價半徑的兩倍 (0.64 Å) 長 0.15 Å。F-F 鍵也相當弱 (鍵解離能 = 155 kJ/mol),相對於 Cl-Cl 鍵 (242 kJ/mol)。透過將額外的鍵長代入 Pauling 公式,我們計算出 F2 分子中的鍵級僅為 0.6,即比 F-F 單鍵弱得多。造成這種情況的物理原因是 F-F 鍵因 F 原子上孤對電子的排斥而“拉伸”。這種擁擠是由於 [He] 1s2 內層軌道以及氟原子的價軌道都被高核電荷收縮造成的。相反,Cl2 中的 Cl 原子具有更大的 [Ne] (1s22s22p6) 內層,因此 Cl-Cl 具有“正常”的單鍵鍵長 (1.98 Å),是 Cl 原子共價半徑的兩倍 (0.99 Å)。類似的孤對電子排斥效應解釋了肼 (H2N-NH2) 和過氧化氫 (HO-OH) 中異常長且弱的 N-N 和 O-O 單鍵,這兩種分子都是高反應性分子。
比較鍵強趨勢時,電負性差異和孤對電子排斥的重要作用很明顯。下表顯示了 p 區元素與 H 和 F 的平均單鍵焓。H 與第二週期元素 (C、N、O、F) 形成的鍵比與第三週期元素 (Si、P、S、Cl) 形成的鍵更強,因為 2p 價電子更靠近原子核,因此比 3p 軌道中的電子形成更強的鍵。與 H 的鍵也遵循預期的趨勢,即隨著電負性差異的增加,鍵強度增加。然而,第二週期元素 (C、N、O、F) 與 F 之間的鍵由於孤對電子排斥而異常弱。因此,Si-F 鍵明顯強於 C-F 鍵,而 C-H 鍵遠強於 Si-H 鍵。強 Si-F 鍵是 HF 蝕刻玻璃 (產生 SiF62- 陰離子) 的原因,而強 C-H 鍵是烴類和其他有機分子穩定性的重要因素。
平均 E-H 和 E-F 鍵焓 (kJ/mol)
| C-H 413 | N-H 391 | O-H 483 | H-F 567 |
| Si-H 323 | P-H 322 | S-H 339 | H-Cl 431 |
|
|
|||
| C-F 485 | N-F 272 | O-F 190 | F-F 155 |
| Si-F 565 | P-F 490 | S-F 327 | Cl-F 253 |

F2 中異常弱的鍵是氟高電負性以及元素氟氣具有傳奇反應性的原因,氟氣與氫和金屬粉末發生爆炸性反應。由於元素氟的不穩定性及其與更具電正性的元素形成的鍵的極性,氟化合物往往非常穩定。例如,稀有氣體 Xe 和 Kr 與氟反應形成共價化合物,而其他鹵素則不反應。氟碳化合物含有強 C-F 鍵,具有很高的熱穩定性和化學穩定性。全氟碳化合物如 特氟龍 (聚四氟乙烯,-(CF2CF2)n-,PTFE) 也是高度疏水的。全氟碳的非凡疏水性源於 -CF2- 和 -CF3 基團比 -CH2- 和 -CH3 基團“更胖”;因此,將它們溶解在水中比溶解烴類更能破壞氫鍵網路。 [21]
1.4 討論問題
[edit | edit source]小組論文專案
加入無機化學課程中的一組同學。每個小組應有 3 或 4 名學生。安排時間見面一個小時左右。在會議之前,閱讀第一部分 (第 1367-1391 頁) 以及 Linus Pauling 關於化學鍵本質的 文章 (J. Am. Chem. Soc. 1931, 53, 1367-1400) 結尾處的摘要。
這篇文章是在薛定諤發展原子軌道的量子力學理論僅僅幾年後發表的,被認為是現代化學史上最重要的文章之一。在會議上,討論以下問題:(1) 在 Pauling 發表這項工作之前,人們對分子中的化學鍵瞭解多少?(2) 這篇論文引入了哪些我們今天仍在使用的概念?(3) 這些想法為什麼重要?(4) Pauling 有沒有犯錯,如果有,是什麼,為什麼?
與你的同學一起,寫一篇 1-2 頁的論文來回答這些問題。請在首頁上列出你小組中所有學生的姓名;你們所有人將在這項作業中獲得相同的成績。將從這些論文中摘錄一些匿名片段與全班同學分享。
本章中的課堂討論問題
- 什麼是等效共振結構?用一些上面沒有涉及的新例子來說明。
- 用一些新的例子解釋無鍵共振和超價鍵。
- 對於含有奇數電子的分子,價鍵理論有哪些侷限性?用一兩個例子說明。
1.5 習題
[edit | edit source]1. 為以下物質繪製組合八隅體結構(包括形式電荷、鍵級和分子形狀):(a) BrO3-、(b) SF6、(c) KrF2、(d) HClO4 (= HOClO3)、(e) NO2- 和 (f) ClO2。
2. 為以下物質繪製組合八隅體結構(包括形式電荷、鍵級和分子形狀):(a) Al2Cl6、(b) SnCl3-、(c) BrF4-、(d) HOClO、(e) SO3 和 (f) NO2+。
3. 使用共振來顯示為什麼甲醯胺 (HCONH2) 中的 CO 鍵距比丙酮中的 CO 鍵距更長。
4. 給出與氨氣等電子結構的五種穩定分子和/或離子的公式。
5. 命名三種與 (a) NO2+、(b) BF4-、(c) CH4 和 (d) HCN 等電子的知名分子或離子。
6. 命名三種與 (a) CN-、(b) H2O、(c) BF3 和 (d) CO2 等電子的知名分子或離子。
7. 乙炔中的 CC 鍵距為 1.20 Å。使用 Pauling 鍵長-鍵強度公式,D(n) = D(1) - 0.6 log(n),估計乙烯酮 (H2CCO) 中的 C-C 鍵距。
8. 在羥胺 H2NOH 中,N-O 鍵距為 1.46 Å。使用 Pauling 鍵長-鍵強度公式,估計 NO2 和 NO3- 中的 N-O 鍵距。
9. 氮可以在含有如 NF4+ 和 NO3- 等離子的化合物中以 +5 氧化態存在。然而,中性二元化合物 NF5 是未知的。你能為這些化合物中的每一個畫出八隅體結構嗎?為什麼 NF5 會不穩定?
10. 考慮化合物 NH3 和 PH3。氨中 H-N-H 鍵角為 108o (接近四面體角,109.5o),但 PH3 中的類似角度為 93o。為什麼 PH3 中的角度更接近 90o 而不是四面體角?
11. N2F3+ 離子的兩種假設結構為 [N-NF3]+ 和 [F-N-NF2]+。哪個更穩定?解釋。(注意:公式中的線可以表示單鍵或多鍵)
12. 二氟化氪 KrF2 在乾冰溫度下分解成 Kr 和 F2。然而,[KrF]+ 離子的幾種鹽相對穩定。為 KrF2 和 [KrF]+ 繪製價鍵圖,顯示孤對電子、可能的共振結構、形式電荷、鍵級和鍵角。為什麼 [KrF]+ 比 KrF2 更穩定?
13. 考慮陰離子 SF3O2- (其中 S 為中心原子)。可能存在多少種異構體?哪一種最穩定?
14. 鹵素間化合物 BrF 中的 Br-F 鍵距為 1.76 Å。使用此資訊估計 BrF3 和 BrF5 中的平均鍵長。
15. BH3 和 BH4- 中的 B-H 鍵距大致相同。然而,BF3 中的 B-F 鍵距比 BF4- 離子中的 B-F 鍵距短。解釋。
16. 肼 (H2N-NH2) 中的 N-N 鍵解離能為 159 kJ/mol。N2 中的 N-N 三鍵解離能為 941 kJ/mol,即遠大於肼中 N-N 單鍵解離能的三倍。解釋為什麼肼中的 N-N 鍵如此弱,以及為什麼這種效應在 N2 中沒有出現。
17. 證明一組四個 sp3 雜化軌道滿足以下條件:(a) sp3 集中任意兩個軌道都是正交的,以及 (b) 軌道是適當地歸一化的。
18. 在量子力學中,沿特定方向 (例如 x 方向) 運動的粒子的動量 (p) 可以透過對它的波函式 進行 動量算符 操作來獲得
- ,其中
知道這個運算元的正確形式是薛定諤提出哈密頓運算元的關鍵,該運算元作用於波函式得到總能量。動量運算元也必須與德布羅意關係p = h/λ一致,該關係將動量與粒子波長聯絡起來。
類比電磁波,薛定諤知道在x方向上自由空間中運動的類波粒子(如電子)可以用波函式描述
其中波數k與粒子的德布羅意波長λ成反比,由k = 2π/λ給出。這裡A是歸一化常數,ω是波的頻率,表示其相位。
使用動量運算元證明對於自由粒子,我們從得到的動量值p與德布羅意關係p = h/λ一致。
(提示:k、ω和與x無關)
19. N3S4+是一個環狀陽離子,不含N-N鍵。繪製七元環的結構,並使用電子計數方法確定單鍵、雙鍵和孤對電子的數量。繪製該離子可能的共振結構,顯示形式電荷,並指出哪個結構最穩定。
20. F的電負性高於Cl,F2的氧化性遠強於Cl2,儘管氟的電子親和能(-328 kJ/mol)低於氯(-349 kJ/mol)。解釋這種明顯的矛盾。
21. 甲烷 (CH4)、氨 (NH3) 和水 (H2O) 中的單鍵分別比SiH4、PH3和H2S中的單鍵強。類似的含氟化合物遵循相反的趨勢:CF4、NF3和OF2中的單鍵比SiF4、PF3和SF2中的單鍵弱。你能解釋這兩種相反的趨勢嗎?
1.6 參考文獻
[edit | edit source]- ↑ G. N. Lewis, "The atom and the molecule," J. Am. Chem. Soc. 1916, 38, 762-785
- ↑ W. Saenger, "The structure of the blue starch-iodine complex," Naturwissenschaften 71, 31-36 (1984).
- ↑ R. D. Hancock and B. J. Tarbet, "The other double helix - the fascinating chemistry of starch," J. Chem. Ed. 77, 988-992 (2000).
- ↑ R. J. Gillespie and B. Silvi, "The octet rule and hypervalence: two misunderstood concepts," Coord. Chem. Rev. 233-234, 53-62 (2002).
- ↑ I. Chung, B. Lee, J. He, R. P. H. Chang and M. G. Kanatzidis, All-solid-state dye-sensitized solar cells with high efficiency, Nature 485, 486-489 (2012). doi:10.1038/nature11067
- ↑ S.D. Stranks, G. E. Eperon, G. Grancini, C. Menelaou, M. J. P. Alcocer, T. Leijtens, L. M. Herz, A. Petrozza, and H. J. Snaith, Electron-Hole Diffusion Lengths Exceeding 1 Micrometer in an Organometal Trihalide Perovskite Absorber, Science 342, 341-344 (2013). DOI: 10.1126/science.1243982
- ↑ G. Xing, N. Mathews, S. Sun, S. S. Lim, Y. M. Lam, M. Grätzel, S. Mhaisalkar, and T. C. Sum, Long-Range Balanced Electron- and Hole-Transport Lengths in Organic-Inorganic CH3NH3PbI3, Science 342, 344-347 (2013). DOI: 10.1126/science.1243167
- ↑ J.-P. Correa-Baena, A. Abate, M. Saliba, W. Tress, T. J. Jacobsson, M. Grätzel, and A. Hagfeldt, The rapid evolution of highly efficient perovskite solar cells, Energy Environ. Sci., 10, 710-727 (2017). DOI: 10.1039/C6EE03397K
- ↑ N. V. Sidgwick and H. M. Powell, Proc. Roy. Soc. A176, 153 (1940),
- ↑ R. J. Gillespie and R. S. Nyholm, Quart. Rev. Chem. Soc., 11, 339 (1957).
- ↑ R. J. Gillespie, "Fifty years of the VSEPR model," Coord. Chem. Rev. 252, 1315-1327 (2008). DOI: 10.1016/j.ccr.2007.07.007
- ↑ Pauling, L. (1932). "化學鍵的本質。IV. 單鍵的能量和原子的相對電負性". J. Am. Chem. Soc. 54 (9): 3570–3582. doi:10.1021/ja01348a011.
- ↑ Mulliken, R. S. (1934). "一個新的電親和力標度;以及關於價態和價態電離勢和電子親和力的資料". J. Chem. Phys. 2 (11): 782–793. Bibcode:1934JChPh...2..782M. doi:10.1063/1.1749394.
- ↑ Mulliken, R. S. (1935). "分子的電子結構XI. 電親和力、分子軌道和偶極矩". J. Chem. Phys. 3 (9): 573–585. Bibcode:1935JChPh...3..573M. doi:10.1063/1.1749731.
- ↑ Pearson, R. G. (1985). "路易斯酸和鹼的絕對電負性和絕對硬度". J. Am. Chem. Soc. 107 (24): 6801. doi:10.1021/ja00310a009.
- ↑ B. Hammer and J. K. Norskov, "為什麼金是所有金屬中最惰性的", 自然 376, 238 - 240 (2002. doi:10.1038/376238a0
- ↑ Schomaker, Verner; Stevenson, D. P. (1941). "共價半徑的一些修正和部分離子單共價鍵長度的加和規則 *". 美國化學會志. 63: 37–40. doi:10.1021/ja01846a007.
- ↑ Pauling, L. 化學鍵的本質,第 3 版;康奈爾大學出版社:紐約伊薩卡,1960 年;第 224 頁。
- ↑ Robinson, Edward A.; Johnson, Samuel A.; Tang, Ting-Hua; Gillespie, Ronald J. (1997). "用幾乎離子模型重新解釋與氟的鍵長". 無機化學. 36 (14): 3022–3030. doi:10.1021/ic961315b. PMID 11669953.
- ↑ Pyykkö, Pekka; Atsumi, Michiko (2009). "元素 Li–E112 的分子雙鍵共價半徑". 化學:歐洲期刊. 15 (46): 12770–12779. doi:10.1002/chem.200901472.
- ↑ V. H. Dalvi and P. J. Rossky, 氟碳疏水性的分子起源,美國國家科學院院刊 107,13603–13607 (2010). DOI: 10.1073/pnas.0915169107.


































![{\displaystyle \chi _{\rm {A}}-\chi _{\rm {B}}={\sqrt {E_{\rm {d}}({\rm {AB}})-[E_{\rm {d}}({\rm {AA}})+E_{\rm {d}}({\rm {BB}})]/2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93475ab1444be44f5df567732672dcef9630e8b3)






