數學物理導論/量子力學中的N體問題/分子

彈簧模型的振動

我們這裡處理一個簡單的分子模型\index{molecule}來強調使用\index{symmetry}在分子研究中的重要性。 水分子 H$_{2}$0 屬於稱為 $C_{2v}$ 的點群。該群由四個對稱操作組成：恆等操作 $E$，旋轉 $C_{2}$ 角度為 $\pi$，以及兩個平面對稱性 $\sigma _{v}$ 和 $\sigma '_{v}$ 相對於透過 $C_{2}$ 操作旋轉軸的兩個平面（見圖 figmoleceau）。

figmoleceau

水分子。 對稱群 $C_{2v}$ 對應於一組操作：恆等操作 $E$，旋轉 $C_{2}$ 角度為 $\pi$ 繞垂直軸，對稱性 $\sigma _{v}$ 相對於垂直於紙張的平面，以及對稱性 $\sigma '_{v}$ 相對於紙張的平面。

群 $C_{2v}$ 是 32 個可能的點群之一 ([ma:group:Jones90][ph:solid:Ashcroft76])。 命名法在圖 ---figsymetr--- 中解釋。

figsymetr

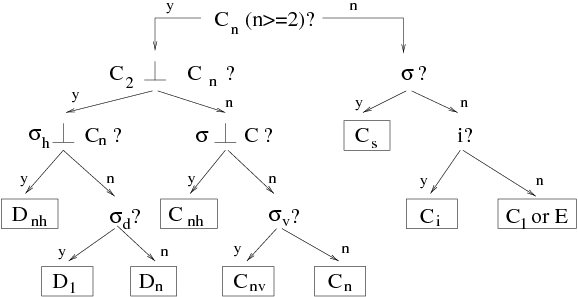化學對稱群的命名法。從樹的頂部開始依次測試對稱操作的出現。根據問題的答案，透過樹進行遍歷，“o”表示是，“n”表示否。$C_{n}$ 表示旋轉角度為 $2\pi /n$，$\sigma _{h}$ 表示關於水平平面（垂直於$C_{n}$ 軸）的對稱操作，$\sigma _{h}$ 表示關於垂直平面（經過$C_{n}$ 軸）的對稱操作，而$i$ 表示反演。群的名稱用框框起來。

這些群中的每一個都可以用“特徵”表來描述，這些特徵表定義了這個群的可能不可約表示\index{不可約表示}。群$C_{2v}$ 的特徵表是

tabchar

群$C_{2v}$ 的特徵群。

$C_{2v}$	$E$	$C_{2}$	$\sigma _{v}$	$\sigma '_{v}$
$A_{1}$	1	1	1	1
$A_{2}$	1	1	-1	-1
$B_{1}$	1	-1	1	-1
$B_{2}$	1	-1	-1	1

群 $C_{2v}$ 的所有表示都是一維的。有四個表示，分別標記為 $A_{1}$，$A_{2}$，$B_{1}$ 和 $B_{2}$。在水分子情況下，九維空間中的 $e_{i}$ $i=1,\dots ,9$。實際上，每個原子由三個座標表示。表示在這裡對應於選擇向量 $e_{i}$ 的一個線性組合 $u$，使得對於對稱群 $g$ 的每個元素，都有

$g(u)=M_{g}u.$

特徵表提供了每個運算 $g$ 的表示矩陣 $M_{g}$ 的跡。由於這裡考慮的所有表示都是一維的，特徵只是 $M_{g}$ 的（唯一）特徵值。圖 figmodesmol 繪製了水分子 $C_{2v}$ 群的九個表示。可以看出，由向量 $e_{i}$ 張成的空間可以被分成九個由運算 $g$ 不變的子空間。引入表示和 ([ma:group:Jones90])，所考慮的表示 $D$ 可以寫成不可約表示的和

$D=3A_{1}\oplus A_{2}\oplus 2B_{1}\oplus 3B_{2}.$

figmodesmol

---

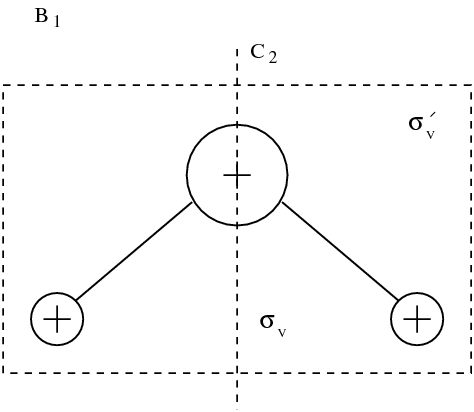
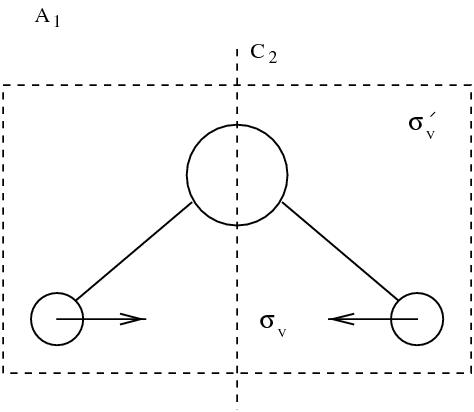
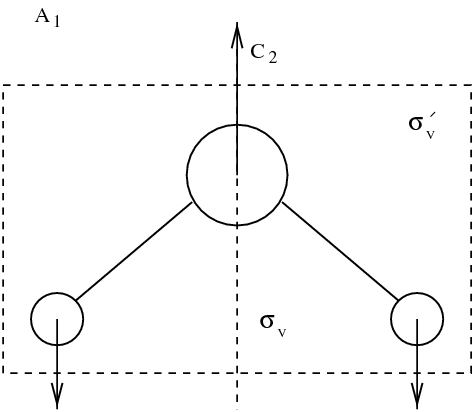
$H_{2}O$ 分子的本徵模態。振動模態用方框框起來。其他模態對應於旋轉和平移。

---

在九種模態中，有三種平移模態和三種旋轉模態。這些模態保持分子原子間距離不變。圖figmodesmol中用方框框起來的是三種真實的振動模態。動力學通常由

${\frac {d^{2}x}{dt^{2}}}=Mx$

定義，其中$x$ 是在$e_{i}$ 基下定義系統狀態的向量。然後在對應於三種振動模態的座標系中對動力學進行對角化。這裡，對稱性考慮足以獲得特徵向量。一旦$M$ 的係數的數值已知，就可以快速地計算出特徵值。

兩個原子核，一個電子

這種情況對應於H$_{2}^{+}$ 分子的研究（[#References|參考文獻]）。我們在這裡使用的玻恩-奧本海默近似假設質子是固定不動的（質子的運動相對於電子的運動很慢）。

注：這個問題可以精確求解。然而，我們在這裡介紹的變分近似可以用於更復雜的情況。

我們在這裡介紹的 LCAO（原子軌道線性組合）方法是變分方法的一個特例。它透過原子的一電子波函式的線性組合來逼近電子波函式[注：即解空間被原子波函式所張成的子空間近似].

$\psi =a\psi _{1}+b\psi _{2}$

更準確地說，讓我們選擇$\phi _{s,1}$ 和 $\phi _{s,2}$ 作為基函式，它們分別是分別以原子$1$ 和 $2$ 為中心的$s$ 軌道。這種近似隨著 R 的增大而變得更加有效（參見圖figH2plusS）。

H$_{2}^{+}$ 分子： 選擇與每個氫原子相關的$1s$ 函式作為變分方法中使用的基函式。

figH2plusS

問題的對稱性導致將特徵向量寫成

${\begin{matrix}\psi _{g}&=&N_{g}(\psi _{1}+\psi _{2})\\\psi _{u}&=&N_{u}(\psi _{1}-\psi _{2})\end{matrix}}$

使用指標符號 $g$ 和 $u$，回想起函式的奇偶性：$g$ 代表德語中的 "gerade"，即偶數，而 $u$ 代表德語中的 "ungerade"，即奇數。圖 figH2plusLCAO 表示這兩個函式。

函式 $\psi _{g}$ 和 $\psi _{u}$ 是基於兩個氫原子 $s$ 軌道進行變分近似問題求解得到的解。

figH2plusLCAO

考慮到哈密頓量，可以使能量簡併，如圖 figH2plusLCAOener 的圖示所示。

使用氫原子 $s$ 軌道作為基底，用 LCAO 方法推匯出的 $H_{2}^{+}$ 分子的能量圖。

figH2plusLCAOener

secnnne

N 個原子核，n 個電子

在這種情況下，對稱性的考慮有助於找到簡化譜問題的特徵子空間。這些考慮與點群表示論有關。當同一分子的原子位於平面上時，該平面就是一個對稱元素。對於線性分子，任何沿著這條直線經過的平面也是對稱平面。可以區分兩種型別的軌道。

定義

軌道 $\sigma$ 在關於對稱平面的反射中保持不變。

定義： 軌道 $\pi$ 在關於該平面的反射中改變符號。

讓我們考慮一個線性分子。其他例子，請參考 ([#References|參考資料])。

例子: 分子 BeH$_{2}$。我們尋找一個在由軌道 $2s$ 和 $z$ 跨越的空間中的波函式，鈹原子 Be 的 $2s$ 和 $z$，以及兩個氫原子的兩個軌道 $1s$。因此空間是四維的（軌道 $x$ 和 $y$ 未被使用），在這個基底上對角化的哈密頓量通常被寫成一個 $4\times 4$ 矩陣。考慮到所考慮分子的對稱性，該矩陣可以寫成一個 *塊對角矩陣*。讓我們選擇以下基底作為狀態空間的近似：\{$2s,z,1s_{1}+1s_{2},1s_{1}-1s_{2}$\}. 然後對稱性考慮表明軌道必須是

${\begin{matrix}\sigma _{s}&=&\alpha _{1}2s+\beta _{1}(1s_{1}+1s_{2})\\\sigma _{s}^{*}&=&\alpha _{2}2s-\beta _{2}(1s_{1}+1s_{2})\\\sigma _{p}&=&\alpha _{3}z+\beta _{3}(1s_{1}-1s_{2})\\\sigma _{p}^{*}&=&\alpha _{4}z-\beta _{4}(1s_{1}-1s_{2})\end{matrix}}$

這些鍵在三個原子之間是離域的，並在圖 figBeH2orb 中進行了描繪。

使用 LCAO 方法研究 $H_{2}^{+}$ 分子。選擇的基底是氫原子的兩個軌道 $s$。}

figBeH2orb

我們有兩個成鍵軌道和兩個反鍵軌道。能級圖在圖 figBeH2ene 中表示。在基態，四個電子佔據兩個成鍵軌道。

使用 LCAO 方法繪製 $H_{2}^{+}$ 分子的能級圖。選擇的基底是氫原子的兩個軌道 $s$。}

figBeH2ene

對分子的實驗研究表明，鍵的特性僅略微依賴於其他原子的性質。因此，問題被簡化為考慮 $\sigma$ 分子軌道是雙中心的，這意味著它位於兩個原子之間。這些軌道被稱為雜化軌道。

示例： 讓我們再次以 BeH$_{2}$ 分子為例。該分子是線性的。這種幾何形狀可以透過 $s-p$ 雜化來很好地描述。

${\begin{matrix}d_{1}&=&{\frac {1}{\sqrt {2}}}(s+z)\\d_{2}&=&{\frac {1}{\sqrt {2}}}(s-z)\end{matrix}}$

與其考慮基底 {$2s,z,1s_{1},1s_{2}$\}，不如直接考慮基底 {$d_{1},d_{2},1s_{1},1s_{2}$\}。因此，從一開始，光譜問題就得到了很好的解決。