數值方法導論/插值

目標

• 理解插值
• 推導牛頓插值公式
• 推導拉格朗日插值公式
• 應用插值方法解決問題
• 使用插值找到離散函式的導數和積分

資源

• 直接法章節
• 牛頓法章節
• 拉格朗日法章節
• 樣條法章節
• 插值的編年史
• NIST 數字數學函式庫

插值

插值 是從一組離散資料點中推匯出一個簡單函式的過程，使該函式透過所有給定的資料點（即精確地再現資料點），並可用於估計給定資料點之間的其他資料點。 這是必要的，因為在科學和工程中，我們經常需要處理離散的實驗資料。 插值還用於透過對資料點進行取樣並使用更簡單的函式對其進行插值來簡化複雜的函式。 多項式通常用於插值，因為它們更容易計算、微分和積分 - 稱為 多項式插值。

可以證明，給定 n+1 個數據點，總能找到一個 n 階/度多項式來透過/再現這 n+1 個點。

直接法

給定 n+1 個數據點，直接法假設以下多項式

$y=f(x)=a_{0}+a_{1}x+a_{2}x^{2}+...+a_{n}x^{n}$

對於 $x$ 的 n+1 個值和相應的 $y$ 的 n+1 個值，我們可以透過解 n+1 個聯立線性方程組來求解 $a_{0},a_{1},...,a_{n}$，這被稱為直接法。

例如，給定兩個資料點 $(x_{0},y_{0})$ 和 $(x_{1},y_{1})$，我們可以使用線性函式 $y=f(x)=a_{0}+a_{1}x$ 來透過這兩個資料點

$y_{0}=a_{0}+a_{1}x_{0}$

$y_{1}=a_{0}+a_{1}x_{1}$

一旦我們求解了 $a_{0}$ 和 $a_{1}$（$f(x)$ 的係數），我們可以使用該函式作為插值的依據——估計其間的缺失資料點。

牛頓法

在牛頓法中，插值函式以 牛頓多項式（又稱牛頓形式）的形式寫出。例如，給定一個數據點 $(x_{0},y_{0})$，我們只能推匯出一個零階多項式： $y=f(x)=a_{0}$。因為 $f(x_{0})=y_{0}$，零階牛頓多項式為 $y=f(x)=y_{0}$。

給定兩個資料點，我們可以將牛頓多項式寫成 $y=f(x)=a_{0}+a_{1}(x-x_{0})$ 的形式。將兩個資料點代入，得到

$a_{0}=y_{0}$

$a_{1}={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}$

顯然，該函式透過這兩個資料點（即準確地再現了這兩個資料點）。該函式在 $x=x_{0}$ 處的導數為 $f'(x_{0})=a_{1}={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}$，與前向差分法的結果一致。

給定三個資料點，我們可以將牛頓多項式寫成

$y=f(x)=a_{0}+a_{1}(x-x_{0})+a_{2}(x-x_{1})(x-x_{0})$

將三個資料點代入，得到

由於 $y_{0}=a_{0}$，我們得到 $a_{0}=y_{0}$

由於 $y_{1}=a_{0}+a_{1}(x_{1}-x_{0})$，我們得到 $a_{1}={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}$

由於 $y_{2}=a_{0}+a_{1}(x_{2}-x_{0})+a_{2}(x_{2}-x_{1})(x_{2}-x_{0})$

我們得到

${\begin{aligned}a_{2}&={\frac {y_{2}-a_{0}-a_{1}(x_{2}-x_{0})}{(x_{2}-x_{1})(x_{2}-x_{0})}}\\&={\frac {y_{2}-y_{0}-{\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}(x_{2}-x_{0})}{(x_{2}-x_{1})(x_{2}-x_{0})}}\\&={\frac {y_{2}-y_{0}-{\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}((x_{2}-x_{1})+(x_{1}-x_{0}))}{(x_{2}-x_{1})(x_{2}-x_{0})}}\\&={\frac {y_{2}-y_{0}-{\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}(x_{2}-x_{1})-(y_{1}-y_{0})}{(x_{2}-x_{1})(x_{2}-x_{0})}}\\&={\frac {y_{2}-y_{1}-{\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}(x_{2}-x_{1})}{(x_{2}-x_{1})(x_{2}-x_{0})}}\\&={\frac {{\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}-{\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}}{x_{2}-x_{0}}}\\\end{aligned}}$

這個三次多項式函式透過所有三個資料點（二階導數和三階導數在 $x_{0}$ 和 $x_{1}$ 處與差商法匹配）。

從這兩個例子中，我們可以看到牛頓多項式的係數遵循一種稱為 差商 的模式。例如，$a_{1}={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}$ 被稱為一階差商（記為 $f[x_{0},x_{1}]$），因為它取決於 $x_{0}$ 和 $x_{1}$。差商符號可以用來寫出一般階（形式）的牛頓多項式

$f(x)=f[x_{0}]+f[x_{0},x_{1}](x-x_{0})+f[x_{0},x_{1},x_{2}](x-x_{0})(x-x_{1})+...$

$+f[x_{0},x_{1},x_{2},...,x_{n}](x-x_{0})(x-x_{1})(x-x_{2})...(x-x_{n-1})$

其中

$a_{0}=f[x_{0}]=y_{0}$，因為根據定義 $f[x_{i}]=y_{i}$

$a_{1}=f[x_{0},x_{1}]={\frac {f[x_{1}]-f[x_{0}]}{x_{1}-x_{0}}}$

$a_{2}=f[x_{0},x_{1},x_{2}]={\frac {f[x_{1},x_{2}]-f[x_{0},x_{1}]}{x_{2}-x_{0}}}$

$\dots$

$a_{k}=f[x_{0},x_{1},x_{2},\dots ,x_{k-1},x_{k}]={\frac {f[x_{1},x_{2},\dots ,x_{k-1},x_{k}]-f[x_{0},x_{1},x_{2},\dots ,x_{k-1}]}{x_{k}-x_{0}}}$

我們可以使用以下表格計算牛頓多項式的係數。

${\begin{matrix}x_{0}&y_{0}=f[x_{0}]&&&\\&&f[x_{0},x_{1}]&&\\x_{1}&y_{1}=f[x_{1}]&&f[x_{0},x_{1},x_{2}]&\\&&f[x_{1},x_{2}]&&f[x_{0},x_{1},x_{2},x_{3}]\\x_{2}&y_{2}=f[x_{2}]&&f[x_{1},x_{2},x_{3}]&\\&&f[x_{2},x_{3}]&&\\x_{3}&y_{3}=f[x_{3}]&&&\\\end{matrix}}$

因為

$f[x_{i}]=y_{i}$

$f[x_{i},x_{i+1}]={\frac {f[x_{i+1}]-f[x_{i}]}{x_{i+1}-x_{i}}}$

下圖展示了差商之間的依賴關係。

例如，給定資料點 $(1,6)$, $(2,11)$, $(3,18)$, 以及 $(4,27)$，我們可以繪製以下表格。

${\begin{array}{|c||c|c|c|c|c|}i&x_{i}&y_{i}&f[x_{i},x_{i+1}]&f[x_{i},x_{i+1},x_{i+2}]&f[x_{i},x_{i+1},x_{i+2},x_{i+3}]\\\hline 0&x_{0}=1&{\begin{aligned}y_{0}&=f[x_{0}]\\&=6\end{aligned}}&{\begin{aligned}f[x_{0},x_{1}]&={\frac {f[x_{1}]-f[x_{0}]}{x_{1}-x_{0}}}\\&={\frac {11-6}{2-1}}\\&=5\end{aligned}}&{\begin{aligned}f[x_{0},x_{1},x_{2}]&={\frac {f[x_{1},x_{2}]-f[x_{0},x_{1}]}{x_{2}-x_{0}}}\\&={\frac {7-5}{3-1}}\\&=1\end{aligned}}&{\begin{aligned}&f[x_{0},x_{1},x_{2},x_{3}]\\&={\frac {f[x_{1},x_{2},x_{3}]-f[x_{0},x_{1},x_{2}]}{x_{3}-x_{0}}}\\&={\frac {1-1}{4-1}}\\&=0\end{aligned}}\\\hline 1&x_{1}=2&{\begin{aligned}y_{1}&=f[x_{1}]\\&=11\end{aligned}}&{\begin{aligned}f[x_{1},x_{2}]&={\frac {f[x_{2}]-f[x_{1}]}{x_{2}-x_{1}}}\\&={\frac {18-11}{3-2}}\\&=7\end{aligned}}&{\begin{aligned}f[x_{1},x_{2},x_{3}]&={\frac {f[x_{2},x_{3}]-f[x_{1},x_{2}]}{x_{3}-x_{1}}}\\&={\frac {9-7}{4-2}}\\&=1\end{aligned}}&\\\hline 2&x_{2}=3&{\begin{aligned}y_{2}&=f[x_{2}]\\&=18\end{aligned}}&{\begin{aligned}f[x_{2},x_{3}]&={\frac {f[x_{3}]-f[x_{2}]}{x_{3}-x_{2}}}\\&={\frac {27-18}{4-3}}\\&=9\end{aligned}}&&\\\hline 3&x_{3}=4&{\begin{aligned}y_{3}&=f[x_{3}]\\&=27\end{aligned}}&&&\\\end{array}}$

四個資料點位於一個二階多項式上，這就是係數 $a_{3}$($f[x_{0},x_{1},x_{2},x_{3}]$) 為零。給定 $[a_{0},a_{1},a_{2}]=[6,5,1]$，結果多項式為

${\begin{aligned}y&=a_{0}+a_{1}(x-x_{0})+a_{2}(x-x_{1})(x-x_{0})\\&=6+5\times (x-1)+1\times (x-2)(x-1)\\&=x^{2}+2x+3\end{aligned}}$

求解牛頓多項式的係數後，我們可以對任何 $x$ 求解多項式函式。牛頓多項式通常被重寫成巢狀形式

$f(x)=a_{0}+(x-x_{0})(a_{1}+(x-x_{1})(a_{2}+(x-x_{2})(a_{3}+...+a_{n}(x-x_{n-1}))...)$,

因為這種插值多項式的巢狀形式更容易計算，因為 x 只在函式中出現 n 次。

例如，三階插值多項式的巢狀形式為

$f(x)=a_{0}+(x-x_{0})(a_{1}+(x-x_{1})(a_{2}+(x-x_{2})a_{3}))$

牛頓法的演算法及其實現可以在這個 Jupyter notebook 中找到。

拉格朗日形式

拉格朗日多項式 是另一種用於多項式插值的表示式。它被稱為一種表示式，因為對於一組給定的不同點，插值多項式是唯一的。我們可以透過不同的方法得到相同的多項式。

拉格朗日表達式將插值多項式指定為

$f_{n}(x):=\sum _{i=0}^{n}L_{i}(x)f(x_{i})$

$L_{i}(x):=\prod _{\begin{smallmatrix}0\leq m\leq n\\m\neq i\end{smallmatrix}}{\frac {x-x_{m}}{x_{i}-x_{m}}}={\frac {(x-x_{0})}{(x_{i}-x_{0})}}\cdots {\frac {(x-x_{i-1})}{(x_{i}-x_{i-1})}}{\frac {(x-x_{i+1})}{(x_{i}-x_{i+1})}}\cdots {\frac {(x-x_{n})}{(x_{i}-x_{n})}},$

其中 $n$ 是多項式的階數。

例如，給定兩個資料點，我們得到 $n=1$ 並且

${\begin{aligned}f(x)&=L_{0}f(x_{0})+L_{1}f(x_{1})\\&={\frac {x-x_{1}}{x_{0}-x_{1}}}f(x_{0})+{\frac {x-x_{0}}{x_{1}-x_{0}}}f(x_{1})\\\end{aligned}}$

顯然，函式曲線經過兩個資料點。一階導數也與差商法的一階導數一致

${\begin{aligned}f'(x)&={\frac {f(x_{0})}{x_{0}-x_{1}}}+{\frac {f(x_{1})}{x_{1}-x_{0}}}\\&={\frac {f(x_{1})-f(x_{0})}{x_{1}-x_{0}}}\\\end{aligned}}$

樣條插值

樣條插值 使用多個多項式函式來插值一組資料點，每個多項式對應兩個相鄰資料點。樣條法是必要的，因為當多項式的階數變大時，多項式插值往往會表現出振盪行為（稱為 龍格現象）。以下 iPython 筆記本展示了一個遇到此問題的例子：[1]

樣條法不是另一種尋找離散函式的多項式插值的方法，而是使用分段多項式（樣條）來避免振盪行為。最常見的樣條插值是線性樣條、二次樣條和三次樣條。 線性插值 使用直線連線每對連續資料點，從而形成分段插值。

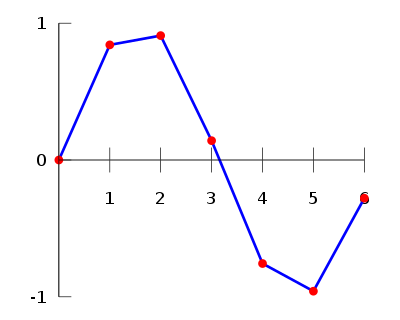
一個 二次樣條 使用二次多項式連線連續資料點。

如果滿足以下條件，則函式 f(x) 是一個二次樣條

1. f(x) 的定義域為區間 [a, b]。
2. $f(x)$ 和 $f'(x)$ 在 [a, b] 上是連續的。
3. 資料點 $x_{i}$ 使得 $a=x_{0}<x_{1}<\dots <x_{n}=b$ 並且 $f(x)$ 在每個子區間 $[x_{i},x_{i+1}]$ 上最多是 2 階多項式。