JPEG - 思想與實踐/霍夫曼編碼
我們與真實JPEG程式的區別在於,在第一部分中,我們使用了易於理解和使用的編碼方法,但效率不高,部分原因是它基於頻率,這些頻率更多地由我們對簡單編碼程式的渴望決定,而不是現實。JPEG使用更高效的霍夫曼編碼和頻率,這些頻率要麼由實際影像決定,要麼由許多典型影像的平均值決定。此外,我們對所有數字使用相同的編碼程式,而JPEG對直流和交流數字使用不同的編碼,並且對Y分量和兩個顏色分量也使用不同的編碼 - 這意味著編碼可能需要超過450個數字的表。
在這裡,我們將選擇基於典型頻率的霍夫曼表,而不是基於對實際影像進行預掃描測量的頻率。因此,我們只需要知道一旦我們有了必要的表格,如何執行霍夫曼編碼和解碼:我們不需要知道這些表格是如何根據頻率構建的。但是,我們將展示構建霍夫曼表的程式。這是一個相當簡單的程式,讀者可能想要編寫一個程式來測量頻率並從實際影像構建霍夫曼表(我們將在附錄2中展示程式)。
假設我們有一些值a1,a2,…,an,這些值附加有頻率,並且需要用程式碼字來表示,以便最常用的值獲得最短的程式碼。這可以透過構建一個所謂的霍夫曼樹來實現,該樹以值作為葉子,並附有頻率。通常,霍夫曼樹可以用多種方式構建,從而產生不同的程式碼長度。JPEG選擇以下方法
我們按頻率遞減的順序排列這些值。對於最後兩個值,我們新增它們的頻率,刪除這兩個值,並在剩餘值中的適當位置插入一個節點(以便頻率仍然遞減 - 注意,如果新頻率出現在其他值中,則可以在多個位置插入)。重複此操作,直到只剩下一個節點,該節點的頻率為1。對於每個操作,我們都刪除了兩樣東西:要麼兩個值,要麼兩個節點,要麼一個值和一個節點。我們透過將值(葉子)放在底部,並依次用線連線被刪除的兩樣東西及其替代節點來構建霍夫曼樹。
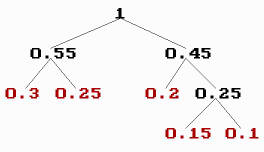
例如,如果值是數字0,1,2,3和4,並且它們的頻率分別是0.3,0.25,0.2,0.15和0.1(總和為1),則刪除過程可能如下所示
- a1 0 0.3 0.3 0.45 0.55 1
- a2 1 0.25 0.25 0.3 0.45
- a3 2 0.2 0.25 0.25
- a4 3 0.15 0.2
- a5 4 0.1
霍夫曼樹可能如下所示
分配給某個值的霍夫曼程式碼的長度是從該值到最後一個節點(頻率為1的頂部節點)的線數。一旦我們知道了分配給這些值的長度(程式碼),我們就可以形成程式碼字,並且可以透過多種方式完成這項工作
透過使用霍夫曼樹,我們可以編碼,例如,當我們從值向頂部節點前進時,向右走寫1,向左走寫0
- 0 00
- 1 10
- 2 01
- 3 011
- 4 111
但我們也可以在沒有霍夫曼樹的情況下進行編碼,重要的是分配給值的程式碼長度。例如,我們可以編碼,使程式碼字的序列(透過它們的二進位制數字表達式識別)遞增:當代碼長度不變時形成連續數字,並且當代碼長度增加時附加零
- 0 00
- 1 01
- 2 10
- 3 110
- 4 111
JPEG使用這種最後一種形成程式碼的方法,因為它解碼速度很快。
在JPEG中,程式碼字不能只由1組成。我們可以透過臨時新增一個額外的值來避免這種情況,該值的頻率是最後一個小值頻率的一半(例如),最後從最大長度的程式碼中刪除一個程式碼。
此外,程式碼字的長度不能超過16。因此,如果霍夫曼樹導致程式碼長度超過16位,則必須依次縮短最長的程式碼。在我們匯入編碼的情況下,我們不需要關心這個問題,但我們將簡要描述它:最長的程式碼長度分配給偶數個值。因此,我們可以將最長長度縮短一位(最後一位),並將此程式碼分配給其中一個值,如果我們能找到另一個(更短的)程式碼給另一個值。假設最後(最長)程式碼有j位,我們可以刪除這些程式碼中的最後一個(長度為j),並將它分別擴充套件為0和1,以便我們獲得兩個新的長度為j+1的程式碼,它們可以替換兩個被刪除的程式碼。
霍夫曼編碼是根據(霍夫曼)值(出現在影像中)和分配給每個值的程式碼長度(由其頻率決定)執行的。因此,我們的出發點是兩個位元組列表:第一個稱為BITS,從1到16,它告訴我們,對於這些數字中的每一個,此程式碼長度的程式碼數量。第二個稱為HUFFVAL,它為每個程式碼長度(具有非零程式碼數量)按順序列出要使用此長度程式碼編碼的值(以及與該長度程式碼數量相同的數量的值)。HUFFVAL中的值稱為霍夫曼值,它們按遞增程式碼長度的順序排列(在給定的程式碼長度內,排序是任意的)。
在我們的程式中,我們使用這些列表來表示Y分量的直流數字
- BITS
- 0 1 5 1 1 1 1 1 1 0 0 0 0 0 0 0
- HUFFVAL
- 0
- 1 2 3 4 5
- 6
- 7
- 8
- 9
- 10
- 11
以及這些列表來表示兩個顏色分量的直流數字
- BITS
- 0 3 1 1 1 1 1 1 1 1 1 0 0 0 0 0
- HUFFVAL
- 0 1 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
最後這些列表表明,存在:長度為1的0個程式碼,長度為2的3個程式碼(編碼霍夫曼值0、1和2),長度為3的1個程式碼(編碼霍夫曼值3),等等。
大多數要編碼的數字是交流數字,它們與直流數字的編碼方式不同。此外,這些值的範圍更大。由於我們引入了霍夫曼編碼,我們必須使用包含所有可能值的列表。
在我們的程式中,我們使用這些列表來表示Y分量的交流數字
- BITS
- 0 2 1 3 3 2 4 3 5 5 4 4 0 0 1 125
- HUFFVAL
- 1 2
- 3
- 0 4 17
- 5 18 33
- 49 65
- 6 19 81 97
- 7 34 113
- 20 50 129 145 161
- 8 35 66 177 193
- 21 82 209 240
- 36 51 98 114
- 130
- 9 10 22 23 24 25 26 37 38 39 40 41 42 52 53 54 55 56 57 58 67 68 69 70 71 72 73 74 83 84 85 86 87 88 89 90 99 100 101 102 103 104 105 106 115 116 117 118 119 120 121 122 131 132 133 134 135 136 137 138 146 147 148 149 150 151 152 153 154 162 163 164 165 166 167 168 169 170 178 179 180 181 182 183 184 185 186 194 195 196 197 198 199 200 201 202 210 211 212 213 214 215 216 217 218 225 226 227 228 229 230 231 232 233 234 241 242 243 244 245 246 247 248 249 250
以及這些列表來表示兩個顏色分量的交流數字
- BITS
- 0 2 1 2 4 4 3 4 7 5 4 4 0 1 2 119
- HUFFVAL
- 0 1
- 2
- 3 17
- 4 5 33 49
- 6 18 65 81
- 7 97 113
- 19 34 50 129
- 8 20 66 145 161 177 193
- 9 35 51 82 240
- 21 98 114 209
- 10 22 36 52
- 225
- 37 241
- 23 24 25 26 38 39 40 41 42 53 54 55 56 57 58 67 68 69 70 71 72 73 74 83 84 85 86 87 88 89 90 99 100 101 102 103 104 105 106 115 116 117 118 119 120 121 122 130 131 132 133 134 135 136 137 138 146 147 148 149 150 151 152 153 154 162 163 164 165 166 167 168 169 170 178 179 180 181 182 183 184 185 186 194 195 196 197 198 199 200 201 202 210 211 212 213 214 215 216 217 218 226 227 228 229 230 231 232 233 234 242 243 244 245 246 247 248 249 250
如果我們把霍夫曼值的個數稱為nhv,那麼我們就有一個數組HUFFVAL[k],從k = 1到nhv,它按列舉順序排列霍夫曼值。從列表BITS[i],我們形成一個數組HUFFSIZE[k],從k = 1到nhv,其中包含程式碼長度i(對於其BITS[i]非零的i),每個i重複BITS[i]次,因此陣列HUFFSIZE[k]與HUFFVAL[k]平行。現在我們構建一個數組HUFFCODE[k],從k = 1到nhv,它指出分配給HUFFVAL[k]的霍夫曼程式碼。我們將一個程式碼用具有程式碼位作為二進位制數字表達式的整數來識別(例如110 = 6),注意,由於程式碼可能以一個或多個零開頭,因此數字表達式必須以零開頭才能得到正確的長度(例如011 = 3)。
程式碼字的生成方式如下:假設我們已經形成了所有長度<= n的程式碼,並且最後一個形成的程式碼是數字c。現在假設下一個程式碼長度是n+i,那麼下一個程式碼是c = 2i∙(c + 1)(透過將i個零連線到c + 1而得到的程式碼),接下來的程式碼是連續數字(c+1,c+2,…),數量與(新)長度n = n+i的程式碼數量相同。在開始時,c設定為0。程式碼編號k,HUFFCODE[k],是分配給霍夫曼值HUFFVAL[k]的程式碼。
為了編碼,我們重新排列列表(陣列)HUFFSIZE和HUFFCODE,使它們成為霍夫曼值的函式(而不是順序號的函式),形成陣列EHUFSI[val]和EHUFCO[val]
- 如果val = HUFFVAL[k],那麼
- EHUFSI[val] = HUFFSIZE[k],並且
- EHUFCO[val] = HUFFCODE[k]
- 如果val = HUFFVAL[k],那麼
注意,EHUFCO[val]是一個數組:EHUFCO[val][j]是程式碼的第j位。
如果我們令函式 *size*(n) (n 為整數) 表示 n 的二進位制表示中數字的個數,並令 *digit*(n) 為數字表示本身(因此 *digit*(n) 是從 1 到 *size*(n) 的一位陣列),那麼構造 HUFFSIZE[k]、HUFFCODE[k]、EHUFSI[val] 和 EHUFCO[val] 的過程(這些過程應用於每個霍夫曼表)可以如下所示。
- k = 1
- i = 1
- j = 1
1
- 如果 j <= bits[i] 則
- 開始
- huffsize[k] = i
- k = k + 1
- j = j + 1
- 轉到 1
- 結束
- 開始
- i = i + 1
- j = 1
- 如果 i <= 16 則
- 轉到 1
- nhv = k - 1
- k = 1
- c = 0
- i = huffsize[k]
2
- huffcode[k] = c
- c = c + 1
- 如果 k = nhv 則
- 轉到 4
- k = k + 1
- 如果 huffsize[k] = i 則
- 轉到 2
3
- c = 2 * c
- i = i + 1
- 如果 huffsize[k] = i 則
- 轉到 2
- 否則
- 轉到 3
4
- k = 1
5
- val = huffval[k]
- e = huffsize[k]
- ehufsi[val] = e
- l = size(huffcode[k])
- dig = digit(huffcode[k])
- 如果 l < e 則
- 對於 j 從 1 到 e - l 做
- ehufco[val, j] = 0
- 對於 j 從 1 到 e - l 做
- 對於 j 從 1 到 l 做
- ehufco[val, e - l + j] = dig[j]
- k = k + 1
- 如果 k <= nhv 則
- 轉到 5
對於上面的 Y 分量的 DC 數字列表,nhv = 12,HUFFSIZE[k] 是序列 2 3 3 3 3 3 4 5 6 7 8 9,HUFFCODE[k] 是序列 00, 010, 011, 100, 101, 110, 1110, 11100, 111000, 1110000, 11100000, 111000000。對於函式 EHUFSI[val] 和 EHUFCO[val],我們有:EHUFSI[0] = 2, EHUFSI[1] = 3, EHUFSI[2] = 3,等等,以及 EHUFCO[0] = 00, EHUFCO[1] = 010, EHUFCO[2] = 011,等等。
在編碼中,對於非負整數 n,我們必須知道 n 的二進位制表示中包含多少位數字。函式 *size*(n) 表示這個數字,它擴充套件到負數 n,讓 -n 與 n 有相同的位數。它由 *size*(0) = 0 和 *size*(n) = trunc(ln(abs(n)) / ln(2) + 0.000001) + 1 當 n != 0 時給出。
- n size
- 0 0
- 1 1
- 2, 3 2
- 4 ... 7 3
- 8 ... 15 4
- 16 ... 31 5
- 32 ... 63 6
- 64 .. 127 7
- 128 .. 255 8
- 256 .. 511 9
- 512 .. 1023 10
- 1024 .. 2047 11
- 等等。
二進位制表示遵循霍夫曼程式碼的整數可以為負數,並且(如 *第一部分* 中所解釋的)我們不需要額外的位來表示這一點:數字表示始終以 1 開頭,我們可以用 0 代替 1。在解碼序列時,以 0 開頭將表明該數字為負數,而 1 後面跟著其餘數字將是數值的二進位制表示。但是,為了表明該數字為負數,JPEG 選擇用其相反的位(形成該數字的 *補碼*)替換 *所有* 數字。因此,如果數字表示以 0 開頭,具有 val 位並且對應於(非負)整數 n,那麼負整數為 -(2val - 1 - n)(在 T.81 中提到,如果數字序列以 0 開頭,並且數字個數為 T,那麼透過將 2T + 1 加到該數字,我們得到數值,但這不正確,當然,該數字是透過將其從 2T - 1 = 11...1(T 個 1)中減去得到的)。
函式 *digit*(n) (n != 0) 的程式,它給出整數 n 的二進位制表示(當 n 為正數時)以及數字表示的補碼(當 n 為負數時)可以如下所示。
- j = size(n)
- 如果 n < 0 則
- n = round(exp(j * ln(2))) - 1 - abs(n)
- 如果 j = 1 則
- digit[1] = n
- 否則
- 開始
- j = j - 1
- q = round(exp(j * ln(2)))
- i = 0
- 當 i <= j 時
- 開始
- i = i + 1
- l = n div q
- n = n - l * q
- q = q div 2
- digit[i] = l
- 結束
- 開始
- 結束
- 開始
**DC 數字:** 對於 DC 數字(64 陣列中的第一個數字),不是數字本身,而是該數字與前面 DC 數字之間的差值 DIFF 進行編碼,並且不是 DIFF 本身,而是表示它所需的位數 val:val = *size*(DIFF)。然後程式碼為 EHUFCO[val],之後是 DIFF 的 val 個二進位制數字:*digit*(DIFF)[j],j = 1,...,val。
**AC 數字:** 63 個 AC 數字(64 陣列中的)以與 DC 數字不同的方式編碼。這裡對實際數字的大小(不是差值)進行編碼,並且由於 AC 陣列中通常存在很多零,因此連續行中這些零的個數與後面非零 AC 數字的大小 *合併*。如果有 m 個零在非零 AC 數字 n 之前,並且 n 的大小為 k,我們將這兩個數字(為半位元組)組合成一個位元組 val = m*16 + k,並且是這個位元組被霍夫曼編碼。然而,這假設 m 和 k 確實是半位元組(也就是說,<= 15)。k 始終 <= 11,但是連續行中可能存在超過 15 個零,因此,當一行零達到 15 並後面跟著另一個零時,我們必須單獨編碼這 16 個零:要編碼的位元組是 val = 15*16 + 0 = 240(稱為 ZRL)。如果 63 個 AC 數字中的最後一個為零,則透過寫入分配給 val = 0*16 + 0 = 0(稱為 EOB,塊結束)的霍夫曼程式碼來表示這一點。在寫入霍夫曼程式碼之後,非零 AC 數字的 k 個二進位制數字以與 DC(或更確切地說 DIFF)數字相同的方式寫入。頻率和程式碼長度分配給所有這些(霍夫曼)值 val = m*16 + k,這些值以這種方式構造(或至少是影像中出現的那些值)。霍夫曼值(要編碼的)的數量最多可以是可能的零的數量(0, 1, ..., 15,即 16)乘以非零 AC 數字的可能大小的數量(即 10),以及除了這個乘積(160)之外,還有兩個額外的值 240 和 0。總共 162 個霍夫曼值。由於我們在這裡選擇匯入基於對大量隨機影像測試的霍夫曼表,因此我們的 AC 霍夫曼表最多包含 162 個值。
解碼
[edit | edit source]對於解碼(當讀取檔案時)(而不是陣列 EHUFSI[val] 和 EHUFCO[val]),我們必須事先從 k = 1 到 16 構造三個陣列:長度為 k 的最小(第一個)程式碼,MINCODE[k],長度為 k 的最大(最後一個)程式碼,MAXCODE[k],以及程式碼(和霍夫曼值)序列中 MINCODE[k] 的 *數量*,VALPTR[k](值指標)。
- j = 0
- k = 0
0
- k = k + 1
- 如果 k > 16 則
- 轉到 fin
- 如果 bits[k] = 0 則
- 開始
- maxcode[k] = -1
- 轉到 0
- 結束
- 開始
- j = j + 1
- valptr[k] = j
- mincode[k] = huffcode[j]
- j = j + bits[k] - 1
- maxcode[k] = huffcode[j]
- 轉到 0
fin
注意,當沒有長度為 k 的程式碼時,MAXCODE[k] = -1,並且 MINCODE[k] 和 VALPTR[k] 未定義。
解碼如下進行:在位流中,要做的第一件事是收集儘可能多的位,使它們形成一個程式碼:我們必須確定在哪裡停止。我們從 k = 0,c = 0 和 MAXCODE[0] = -1(因此 c > MAXCODE[0])開始,並且對於每個讀取的位,我們將它加入 c 並將 k 增加 1,直到 c <= MAXCODE[k]。由於我們將程式碼與數字標識,因此連線意味著我們將 c 設定為 2*c + bit,對於每個新位(稱為 bit)。然後程式碼為 c,我們將找到分配給 c 的霍夫曼值 val,這是具有數字 k = VALPTR[k] + c - MINCODE[k] 的霍夫曼值,因此 val = HUFFVAL[k]
- k = 0
- c = 0
- 當 c > maxcode[k] 時
- 開始
- nbit
- c = 2 * c + bit
- k = k + 1
- 結束
- 開始
- val = huffval[valptr[k] + c - mincode[k]]
這裡 *nbit* 是稍後描述的過程,它讀取下一個位。