計算機科學邏輯/命題邏輯

命題邏輯

命題邏輯是介紹邏輯基本性質的一個很好的工具。它不提供確定原子語句的有效性（真或假）的方法。相反，它允許你在給定其原子成分的有效性的情況下評估複合語句的有效性。

例如，考慮以下情況

我喜歡帕特或者我喜歡喬。

如果我喜歡帕特，那麼我喜歡喬。

我喜歡喬嗎？

接受前兩個陳述作為事實，注意這裡“或”的使用不是排他的，因此實際上可以認為是在說“我喜歡帕特，或者我喜歡喬，或者我兩者都喜歡”。這些陳述是否意味著“我喜歡喬”為真？試著說服自己“我喜歡喬”為真，並考慮另一條推理途徑

豬會飛或者魚會唱歌。

如果豬會飛，那麼魚會唱歌。

魚會唱歌嗎？

我們可以看到，在這兩種情況下答案都是是。以上兩組陳述都可以抽象如下

${\begin{aligned}&P\lor Q\\&P\to Q\\&Q\end{aligned}}$?

在這裡，我們關注的是邏輯推理本身，而不是陳述。因此，我們不使用豬或帕特，而是簡單地寫$Q$s或$P$s。我們首先從命題邏輯的語法開始我們的研究：也就是說，我們描述邏輯語言中的元素以及它們是如何書寫的。然後我們描述這些符號的語義：即符號的含義。

語法

命題邏輯的語法由命題符號、邏輯連線詞和括號組成。規則規定了這些元素如何組合在一起。首先，我們將命題符號僅僅視為一些符號的集合，出於我們的目的，我們將使用羅馬和希臘字母，並將所有符號的集合稱為${\text{Prop}}$

命題符號：一些符號的集合${\text{Prop}}$。例如$p,q,r,\ldots$

其次，我們有邏輯連線詞

邏輯連線詞：$\land ,\lor ,\neg ,\to$

請注意，這些不是最小的必需集合；它們可以使用單個連線詞NOR（非或）或NAND（非與）等效地表示，這些連線詞在計算機硬體的最低級別使用。最後，我們使用括號來表示表示式（稍後我們將使括號可選）

括號：$(,)$

表示式是命題符號、括號和邏輯連線詞的字串。

我們考慮的表示式稱為公式。公式集${\textrm {Form}}$是最小的表示式集，滿足

1. ${\text{Prop}}\subseteq {\text{Form}}$
2. 如果$\phi ,\psi \in {\text{Form}}$，則
   1. $(\phi \land \psi )\in {\text{Form}}$ ,
   2. $(\phi \lor \psi )\in {\text{Form}}$ ,
   3. 若 $(\phi \to \psi )\in {\text{Form}}$，並且
   4. $(\neg \phi )\in {\text{Form}}$ .

另一種定義公式的方法是將其視為由以下上下文無關文法定義的語言（起始符號為 ${\text{Form}}$）

${\text{Form}}\Rightarrow {\text{Prop}}$，其中 ${\text{Prop}}$ 代表任何命題符號

${\begin{aligned}{\text{Form}}\Rightarrow ({\text{Form}}\land {\text{Form}})\\{\text{Form}}\Rightarrow ({\text{Form}}\lor {\text{Form}})\\{\text{Form}}\Rightarrow ({\text{Form}}\to {\text{Form}})\\{\text{Form}}\Rightarrow (\neg {\text{Form}})\end{aligned}}$

事實 1（唯一可讀性）：上述上下文無關文法是無歧義的。

語義

公式的功能是在給定原子語句的含義的情況下建立語句的含義。公式 $\phi$ 的語義，其中命題符號為 $p_{1},\ldots ,p_{n}$，是一個對映，它將每個真值賦值 $V$ 到 $p_{1},\ldots ,p_{n}$ 關聯到 $\phi$ 的一個真值（0 或 1）。（真值“真”和“假”可以分別用 1 或 0 代替，以及縮寫“T”和“F”。）

由於事實 1（如上所示），語義是明確定義的。

指定邏輯連線詞語義的一種方法是透過真值表

$p$	$q$	$p\land q$（p 且 q）
0	0	0
0	1	0
1	0	0
1	1	1

是否總能找到一個實現任何給定語義的公式？是的，任何真值表都可以由一個公式實現。該公式可以如下找到。“表示”其中 $\phi =1$ 的行，使用真命題符號的合取和假命題符號的否定。最後寫出結果的析取。

例如，

$p$	$q$	$\phi$	合取（僅真值）
0	0	1	$\neg p\land \neg q$
0	1	0
1	0	1	$p\land \neg q$
1	1	0

$\phi :(p\land \neg q)\lor (\neg p\land \neg q)$

推論：每個公式都等價於命題符號或命題符號的否定構成的合取式的析取（析取正規化，DNF）。

DNF 的對偶是合取正規化，CNF。

要得到CNF 中的$\phi$

1. 描述$\phi$ 為假的場景。
2. 注意，當$\neg \psi$ 為假時，$\phi$ 為真。因此，使用德摩根定律對$\psi$ 取反。

在某些情況下，DNF（或 CNF）的大小會比原始公式指數級增長。例如，對於$(x_{1}\lor y_{1})\land \cdots \land (x_{n}\lor y_{n})$，其等價的 DNF 的大小是指數級的。

每個真值表是否都存在一個多項式大小的公式來實現它？更準確地說，是否存在$k$ 使得每個具有$n$ 個命題符號的真值表都存在一個大小為$\leq n^{k}$ 的形式$\phi$？答案：否。

證明：假設存在這樣的$k$ 。對於$n$ 個命題符號，真值表的數量是$2^{2^{n}}$ 。大小為$\leq n^{k}$ 的公式數量是$(n+6)^{n^{k}}$（$n$ 個命題符號，4 個連線詞和括號）。顯然，$(n+6)^{n^{k}}<2^{2^{n}}$，對於足夠大的$n$。

[待補充：解釋這些定義是什麼以及提供它們的上下文]

• 滿足性：公式$\phi$ 被真值指派$\tau$ 滿足。記號：$\tau \models \phi$（$\phi$ 對$\tau$ 為真）。
• 蘊涵：公式集$\Sigma$ 蘊涵$\phi$。記號：$\Sigma \models \phi$。$\Sigma$ 蘊涵$\phi$ 當且僅當每個滿足$\Sigma$ 的真值指派也滿足$\phi$。

特別感興趣的公式類別

• ${\text{VALID}}$ – 公式集，其總是為真（也稱為**重言式**）。例如，$(p\lor \neg p),(p\to p),([(p\lor q)\land (p\to q)]\to q)$ 是有效的公式。
• ${\text{UNSAT}}$ – 公式集，其永遠為假（不可滿足）。
• 介於兩者之間：${\text{SAT}}$ - 公式集，其存在滿足賦值（不可滿足）。

注意。 $\phi \in {\text{VALID}}\iff \neg \phi \in {\text{UNSAT}}$。

斷言：$\Sigma \models \phi \iff (\Sigma \cup \{\neg \phi \})\in {\text{UNSAT}}$

斷言：${\text{SAT}}$ 是NP完全的。

證明:

• ${\text{SAT}}\in {\text{NP}}$ : 猜測一個滿足賦值，然後驗證公式是否為真（滿足賦值是一個證書）。

• 硬度。圖3著色 $\in {\text{NP}}$（也存在一個直接證明）。我們將3著色規約到 ${\text{SAT}}$。令 $G=(V,E)$ 為一個圖，其中有 $n$ 個節點 $\{1,\ldots ,n\}$。我們使用命題變數 $p_{i,g},p_{i,r},p_{i,b}$ 來表示節點 $i$ 被染成綠色、紅色或藍色。構造 $\phi$ 如下

${\begin{aligned}\phi =&\bigwedge _{i=1}^{n}{\bigl (}(p_{i,g}\land \neg p_{i,r}\land \neg p_{i,b})\lor (p_{i,r}\land \neg p_{i,g}\land \neg p_{i,b})\lor (p_{i,b}\land \neg p_{i,r}\land \neg p_{i,g}){\bigr )}\\&\wedge \bigwedge _{(i,j\in E)}\neg (p_{i,g}\land p_{j,g})\land \neg (p_{i,r}\land p_{j,r})\land \neg (p_{i,b}\land p_{j,b})\end{aligned}}$

斷言： $G\in {\text{3-Coloring}}\iff \phi \in {\text{SAT}}$。

也可以直接證明 ${\textrm {SAT}}\in {\text{NP}}$。

斷言： ${\text{VALID}}\in {\text{coNP}}$。

Horn子句

SAT在多項式時間內解決的特殊情況。示例

$(p\lor \neg q\lor r)\land (\neg p\lor q\lor \neg r)$

**霍恩子句**（Horn clause）是指最多隻有一個肯定文字（positive literal）的文字析取式（disjunction of literals）。霍恩子句主要有兩種型別。

1. 子句包含1個肯定文字
   1. $p$，或者
   2. $p\lor \neg x_{1}\lor \cdots \lor \neg x_{k}:x_{1}\land \cdots \land x_{k}\to p$
2. 不包含肯定文字
   1. $\neg x_{1}\lor \cdots \lor \neg x_{k}:\neg (x_{1}\land \cdots \land x_{k})$
   2. $x_{1}\land \cdots \land x_{k}\to {\text{false}}$

**斷言**：對於任意一組霍恩公式集$\Sigma$，檢查$\Sigma$ 是否可滿足（satisfiable）屬於**P**類問題。

證明思路：令$\Sigma _{1}$ 為 $\Sigma$ 的子集，其中僅包含型別 1 的子句，而 $\Sigma _{2}$ 為 $\Sigma$ 的子集，其中包含型別 2 的子句。首先要注意的是，$\Sigma _{1}$ 是可滿足的。為了得到一個最小滿足賦值 $\sigma$，從單文字子句中的文字開始，並應用規則。現在需要檢查 $\sigma$ 與 $\Sigma _{2}$ 中的子句的一致性。為此，只需檢查對於 $\Sigma _{2}$ 中的每個子句 $x_{1}\land \cdots \land x_{k}\to {\text{false}}$，$\sigma$ 對於所有的 $x_{1},\ldots ,x_{k}$ 都不為真。

示例：考慮霍恩子句集 $\Sigma$

${\begin{aligned}&p\\&q\\&r\\&\neg p\lor \neg q\lor s\\&\neg s\lor \neg r\lor t\\&\neg t\end{aligned}}$

型別 1 的子句集 $\Sigma _{1}$ 由前 5 個子句組成，而 $\Sigma _{2}$ 由最後一個子句組成。請注意，$\Sigma _{1}$ 也可以寫成

${\begin{aligned}&p\\&q\\&r\\&p\land q\to s\\&s\land r\to t\end{aligned}}$

對於 $\Sigma _{1}$，其最小滿足賦值如下獲得

1. 從 $\{p,q,r\}$ 開始
2. 利用第一個蘊含式推匯出 $s$
3. 利用第二個蘊含式推匯出 $t$

因此，最小滿足賦值使得 $\{p,q,r,s,t\}$ 為真。這與 $\Sigma _{2}$ 矛盾，後者指出 $t$ 必須為假。因此，$\Sigma$ 不可滿足。

演繹系統

**演繹**系統是一種從給定陳述中證明新陳述的機制。

令 $\Sigma$ 為一組已知的有效陳述（命題公式）。在演繹系統中，有兩個組成部分：推理規則和證明。

推理規則

推理規則表明，如果某些陳述（公式）集 $\varphi _{1},\ldots ,\varphi _{k}$ 為真，則給定陳述 $\varphi$ 也必須為真。推理規則 $H$ 表示為 $H:{\frac {\varphi _{1},\ldots ,\varphi _{k}}{\varphi }}$。

示例（肯定前件）： ${\frac {p,~~p\to q}{q}}$

證明

從$\Sigma$中證明$\varphi$的證明是一個公式序列$\varphi _{1},\ldots ,\varphi _{n}$，其中$\varphi _{n}=\varphi$，並且對於所有$i\leq n$

• 每個公式$\varphi _{i}\in \Sigma$，或者
• 存在公式的子集$\varphi _{i_{1}},\ldots ,\varphi _{i_{k}}:i_{1},\ldots ,i_{k}<i$，使得${\frac {\varphi _{i_{1}},\ldots ,\varphi _{i_{k}}}{\varphi _{i}}}$是一個推理規則。

如果$\varphi$使用推理規則$H$從$\Sigma$ 有一個證明，我們寫成$\Sigma \vdash _{H}\varphi$。

性質:

• 可靠性（Soundness）：如果$\Sigma \vdash _{H}\varphi$，則$\Sigma \models \varphi$（即，所有可證明的句子都是真的）。此屬性對於演繹系統正確性的基礎。
• 完備性（Completeness）：如果$\Sigma \models \varphi$，則$\Sigma \vdash _{H}\varphi$（即，所有真句子都是可證明的）。這是演繹系統中一個理想的性質。

自然演繹

自然演繹是一組推理規則。令$\perp$表示矛盾，假。以下是自然演繹的推理規則

1. $\left\{{\frac {\varphi ,\psi }{\varphi \land \psi }}\right.$
2. $\left\{{\frac {\varphi \land \psi }{\varphi }}\right.$}
3. $\left\{{\frac {\varphi \land \psi }{\psi }}\right.$}
4. $\left\{{\frac {\varphi ,\varphi \to \psi }{\psi }}\right.$}
5. $\left\{{\frac {\varphi ,\neg \varphi }{\perp }}\right.$}
6. $\left\{{\frac {\neg (\neg \varphi )}{\varphi }}\right.$}
7. $\left\{{\frac {\perp }{\varphi }}\right.$}
8. $\left\{{\frac {\varphi \to \psi ,\psi \to \varphi }{\varphi \leftrightarrow \psi }}\right.$}
9. $\left\{{\frac {\varphi \leftrightarrow \psi }{\varphi \to \psi }}\right.$}
10. $\left\{{\frac {\varphi \leftrightarrow \psi }{\psi \to \varphi }}\right.$}
11. $\left\{{\frac {\varphi }{\varphi \lor \psi }}\right.$}
12. $\left\{{\frac {\psi }{\varphi \lor \psi }}\right.$}
13. ${\begin{cases}{\dfrac {\begin{matrix}\varphi \\\vdots \\\psi \end{matrix}}{\varphi \to \psi }}\end{cases}}$}

14. ${\begin{cases}{\dfrac {\begin{matrix}\varphi \\\vdots \\\perp \end{matrix}}{\neg \varphi }}\end{cases}}$
15. ${\begin{cases}{\dfrac {\begin{matrix}\neg \varphi \\\vdots \\\perp \end{matrix}}{\varphi }}\end{cases}}$
16. ${\begin{cases}{\dfrac {\begin{matrix}\varphi \lor \psi &\varphi &\psi \\&\vdots &\vdots \\&\rho &\rho \end{matrix}}{\rho }}\end{cases}}$

規則 (13) 允許我們證明形如“如果 $\varphi$ 則 $\psi$” 的有效陳述，即使我們不知道 $\varphi$ 陳述的真值（即，$\varphi$ 不在已知有效陳述的集合 $\Sigma$ 中）。實際上，對於此規則，我們首先假設 $\varphi$ 是有效的。如果我們可以在 $\Sigma \cup \varphi$ 有效的世界中得出結論 $\psi$ 是有效的，那麼我們得出結論關係 $\varphi \to \psi$ 為真，並且我們“釋放”假設 $\varphi$ 是有效的。

現在我們展示如何應用上述推理規則。

示例：否定的或表示式的德摩根定律指出

$\neg (\varphi \lor \psi )\leftrightarrow (\neg \varphi \land \neg \psi )$

證明：根據規則 $(8)$，如果我們能證明 $\neg (\varphi \lor \psi )\to (\neg \varphi \land \neg \psi )$ 和 $(\neg \varphi \land \neg \psi )\to \neg (\varphi \lor \psi )$，我們就可以推匯出期望的結果。

為了證明第一個方向，我們使用規則 13 並假設前提 $\neg (\varphi \vee \psi )$。然後

$\neg (\varphi \lor \psi )$ （假設）

$\varphi$ （假設）

$\varphi \lor \psi$ （根據規則11）

$\perp$ （根據規則5）

$\neg \varphi$ （根據規則14）

$\psi$ （假設）

$\varphi \lor \psi$ （根據規則11）

$\perp$ （根據規則5）

$\neg \psi$ （根據規則14）

$\neg \varphi \land \neg \psi$ （根據規則1）

$\neg (\varphi \lor \psi )\to (\neg \varphi \land \neg \psi )$ （根據規則13）

我們現在證明第二個方向。

$\neg \varphi \land \neg \psi$ （假設）

$\neg \varphi$ （根據規則2）

$\neg \psi$ （根據規則3）

$\varphi \lor \psi$ （假設）

$\varphi \psi$ （假設）

$\perp \perp$ （根據規則5）

$\perp$（根據規則16）

$\neg (\varphi \lor \psi )$ （根據規則14）

$(\neg \varphi \land \neg \psi )\to \neg (\varphi \lor \psi )$ （根據規則13）

皮爾斯定律的證明

$[(A\to B)\to A]\to A$

$(A\to B)\to A$ （假設）(1*)

$\neg A$ （假設）

$A$ （假設）

$\perp$ （根據規則5）

$B$ （根據規則7）

$A\to B$ （根據規則13）

$A$ （根據假設(1*)和規則4）

$\perp$ （根據規則5）

$A$ （根據規則14）

$[(A\to B)\to A]\to A$ （根據規則13）

事實2：自然演繹是可靠的。

為了證明自然演繹也是完備的，我們需要引入命題歸結。

命題歸結

歸結是另一種用於檢查語句有效性的過程。它涉及子句、公式和單個歸結規則。

一些術語

子句

子句是由文字析取組成的命題公式。例如 $p\lor q\lor \neg r$ 。它通常表示為文字的集合，例如 $\{p,q,\neg r\}$ 。

空子句，表示為一個空框“$\Box$”，是沒有文字的析取。它總是假的。

公式

一組子句，每個子句都是可滿足的。例如，${\bigl \{}\{p,\neg q\},\{r\},\{\neg r,s\}{\bigr \}}$表示CNF公式 $(p\lor \neg q)\land (r)\land (\neg r\lor s)$。

空公式，表示為 $\varnothing$ ，是不包含任何子句的集合。它總是真的。

歸結規則

規則規定，給定兩個子句$C$（包含某個文字$y$）和$C'$（包含某個文字$\neg y$），可以推匯出一個新的子句，稱為$C$和$C'$的結果子句（相對於$y$）。

歸結證明系統包含單個歸結規則，其中結果子句定義如下。假設$C$和$C'$是子句，使得$y\in C$且$\neg y\in C'$，則

${\text{Res}}_{y}(C,C')=(C-\{y\})\cup (C'-\{\neg y\})$

包含$\varphi$且在歸結下封閉的最小子句集記為${\text{Res}}(\varphi )$。

示例：如果$C=\{p,y\}$且$C'=\{q,\neg y\}$，則${\text{Res}}_{y}(C,C')=\{p,q\}$。

可以證明，如定義的那樣，歸結規則計算出的子句可以透過自然演繹推匯出來。

斷言：設 $C$ 和 $C'$ 是任意兩個子句，使得 $y\in C$ 且 $\neg y\in C'$ 。則 $C\land C'\implies {\text{Res}}_{y}(C,C')$ 。

為了證明一個陳述 $\psi$ 的有效性，我們將證明其否定陳述 $\neg \psi$ 是不可滿足的。為了證明公式 $\varphi$ 的不可滿足性，我們需要定義公式 $\varphi$ 的歸結反駁。

公式 $\varphi$ 的歸結反駁樹是一棵根節點為空子句的樹，其中每個葉子節點都是 $\varphi$ 中的一個子句，每個內部節點都計算為其兩個對應子節點的歸結式。

注意，$\varphi$ 的子句可以重複作為葉子節點出現。根據上述斷言，我們可以得出結論：

斷言：如果存在公式 $\varphi$ 的歸結反駁樹，則 $\varphi \implies \Box$ ，也就是說，$\varphi$ 是不可滿足的。

示例：公式

$\varphi =(p\lor q)\land (\neg q\lor r)\land (\neg r)\land (\neg p\lor \neg s)\land (s\lor \neg t)\land (t)$

具有以下歸結反駁樹

在計算歸結反駁樹時，選擇子句計算歸結式的順序很重要，如下例所示：考慮公式

$\psi =(p\lor q)\land (\neg q\lor r)\land (\neg p)\land (\neg q)$

即使對於$\psi$可能存在歸結反駁樹，但在嘗試構建樹時，順序也很重要。下面是兩個不同的歸結反駁樹，但只有一個是成功的。

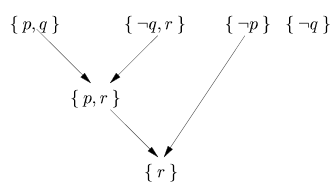對$\psi$進行歸結反駁樹的不成功嘗試

對$\psi$進行歸結反駁樹的成功嘗試

命題歸結的性質

可靠性：命題歸結是可靠的，也就是說，如果對於給定的公式$\varphi$存在歸結反駁樹，則$\varphi$必須是不可滿足的。

定理：對於任何公式$\varphi$，如果$\Box \in Res(\varphi )$，則$\varphi \implies \Box$。

完備性：命題歸結是完備的，也就是說，如果給定的公式$\varphi$是不可滿足的，則$\varphi$具有歸結反駁樹。

定理：對於任何公式$\varphi$，如果$\varphi \implies \Box$，則$\Box \in Res(\varphi )$。

證明：透過對$\varphi$中變數個數進行歸納。

基礎情況：我們有一個變數，比如$p$。$\varphi$的所有可能的子句是$\{p\}$和$\{\lnot p\}$。如果$\varphi$是不可滿足的，則這兩個子句都會出現，因此$\Box \in Res(\varphi )$。

歸納步驟：假設對於少於$n$個變數的公式，該假設成立。令$\varphi$為一個具有$n$個變數的公式。假設$\Box \notin Res(\varphi )$；我們將證明$\varphi$是可滿足的。令$p$為$\varphi$的一個變數。那麼要麼$\{p\}\notin Res(\varphi )$，要麼$\{\lnot p\}\notin Res(\varphi )$（如果兩者都成立，則$\Box \in Res(\varphi )$立即成立）。

假設$\{\lnot p\}\notin Res(\varphi )$。我們定義公式$\varphi ^{p}$，它包含所有不包含$\{p\}$的子句，並且其中文字$\lnot p$已從每個子句中刪除（換句話說，$\varphi ^{p}$等價於將$p$設定為真的結果得到的公式）。

形式上，

$\varphi ^{p}=\{C-\{\lnot p\}:C\in \varphi ,\,p\notin C\}$.

首先，注意

$Res(\varphi ^{p})=\{C-\{\lnot p\}:C\in Res(\varphi ),\,p\notin C\}$

因此，

$\{\lnot p\}\notin Res(\varphi ^{p})$.

此外，由於 $\Box \notin Res(\varphi )$，我們有 $\Box \notin Res(\varphi ^{p})$。根據歸納假設，$\varphi ^{p}$ 是可滿足的。然後 $\varphi$ 透過 $\varphi ^{p}$ 的滿足賦值的擴充套件來滿足，其中 $p$ 等於真。情況 $\{p\}\in Res(\varphi )$ 類似。

自然演繹的完備性

定理：令 $H$ 為自然演繹的推理規則集。如果 $\Sigma \models \varphi$，則 $\Sigma \vdash _{H}\varphi$。

自然演繹完備性證明的思想如下。假設 $\varphi$ 是有效的（那麼 $\lnot \varphi$ 是不可滿足的）。然後我們證明存在一個針對 $\varphi$ 的歸結反駁，然後透過應用矛盾規則（規則 15）

${\frac {\begin{matrix}\neg \varphi \\\vdots \\\perp \end{matrix}}{\varphi }}$

我們得出結論 $\varphi$ 可以被推斷出來。

證明：（草圖）給定一個在 $\Sigma$ 下有效的公式 $\varphi$，我們執行以下步驟

1. 證明 $\lnot \varphi$ 等價於某個 $\psi$，其中 $\psi$ 為合取正規化。
2. 證明對於所有 $\psi$，都有 $\psi \implies Res(\psi )$ 成立。
3. 根據歸結原理的完備性，如果 $\psi$ 是不可滿足的，則 $\Box \in Res(\psi )$。因此，對於某個文字 $p$，有 $\{p\}$ 和 $\{\lnot p\}\in Res(\psi )$。這意味著 $Res(\psi )\implies \bot$。
4. 得出結論 $\lnot \varphi \implies \bot$，因此 $\varphi$ 是有效的。

步驟 (1) 可以透過重複應用德摩根定律輕鬆完成。步驟 (2) 可以使用自然演繹法證明。最後，步驟 (3) 可以透過對獲得 $Res(\psi )$ 的步驟數進行歸納證明。顯然，每個步驟都可以使用自然演繹法模擬。

任何命題歸結演算法在最壞情況下都可能需要很長時間（回想一下，檢查公式 $\varphi$ 的有效性是 co-NP 完全的）。

線性歸結和 PROLOG

線性歸結是一種特殊的歸結策略，它總是將最新的歸結式與一個子句進行歸結。因此，由此獲得的歸結反駁樹是線性的。可以證明，如果子句集是 Horn 子句，則對於任何公式都存在一種線性歸結策略。也就是說，線性歸結對於 Horn 子句集是完備的。

PROLOG 語言使用霍恩子句集上的歸結原理。每個子句稱為程式子句。此外，由單個文字組成的子句稱為事實。只有一個否定文字的子句稱為查詢。下表顯示了不同表示法的比較。在 PROLOG 中，要查詢語句$t$，其思路是將語句取反（$\lnot t$），並使用已知真語句集執行歸結。如果找到一個歸結反駁樹，則語句$t$ 由程式蘊含。

示例：線性歸結用於公式的示例

$\phi =(p)\land (q)\land (r)\land (t\lor \lnot s\lor \lnot r)\land (s\lor \lnot p\lor \lnot q)\land (\lnot t)$

如下所示