SATCHMO 定理證明器是最早使用模型生成的系統之一,即自下而上的證明過程。該證明器由一個小型的 Prolog 程式給出,該程式實現了一個表格證明過程。一個限制是,它需要範圍受限公式。
一階子句  稱為 *範圍受限*,如果出現在頭部
稱為 *範圍受限*,如果出現在頭部  中的每個變數也出現在主體
中的每個變數也出現在主體  中。
中。
- 將子句轉換為範圍受限形式

- 在 Prolog 資料庫中斷言範圍受限子句和 dom 子句。
- 呼叫 satisfiable
kill satisfiable :- assume(X) :- asserta(X).
(Head <- Body) assume(X) :-
Body, not Head, !, retract(X), !, fail.
component(HLit, Head), component(E, (E ; _)).
assume(HLit), component(E, (_ ; R)) :-
not false, !, component(E, R).
satisfiable. component(E, E).
satisfiable.
透過級別飽和修改實現一階完備性。該證明過程在地面情況下實現了超表格。

所有開放分支僅包含正文字。以以下子句集為例 
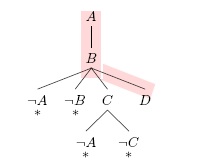
一個 *文字樹* 是一個對  ,由一個有限的、有序的樹
,由一個有限的、有序的樹  和一個標記函式
和一個標記函式  組成,該函式將文字分配給
組成,該函式將文字分配給  的每個非根節點。
的每個非根節點。
在一個有序樹  中,節點
中,節點  的 後繼序列 是所有直接前驅為
的 後繼序列 是所有直接前驅為  的節點的序列,按照
的節點的序列,按照  給出的順序排列。
給出的順序排列。
一組子句  的 (子句)真值表
的 (子句)真值表  是一個文字樹
是一個文字樹  ,其中,對於
,其中,對於  中的每個後繼序列
中的每個後繼序列  ,分別標記為文字
,分別標記為文字  ,都存在一個替換
,都存在一個替換  和一個子句
和一個子句  ,使得對於每個
,使得對於每個  都有
都有  。
。  稱為 真值表子句,真值表子句的元素稱為 真值表文字。
稱為 真值表子句,真值表子句的元素稱為 真值表文字。
A branch of a tableau  is a sequence
is a sequence  (
( ) of nodes in
) of nodes in  such that
such that  is the root of
is the root of  ,
,  is the immediate predecessor of
is the immediate predecessor of  for
for  , and
, and  is a leaf of
is a leaf of  . We say branch
. We say branch  is a prefix of branch
is a prefix of branch  , written as
, written as  or
or  , iff
, iff  for some nodes
for some nodes  ,
,  . The branch literals of branch
. The branch literals of branch  are the set
are the set  . We find it convenient to use a branch in place where a literal set is required, and mean its branch literals. For instance, we will write expressions like
. We find it convenient to use a branch in place where a literal set is required, and mean its branch literals. For instance, we will write expressions like  instead of
instead of  .
.
為了記住一個分支包含矛盾這一事實,我們允許將一個分支標記為 開放 或 封閉。如果真值表中的每個分支都是封閉的,那麼該真值表是 封閉 的,否則它是 開放 的。
選擇函式是一個全函式  ,它將一個開放的 tableau 對映到它的一個開放分支。如果
,它將一個開放的 tableau 對映到它的一個開放分支。如果  ,我們也說
,我們也說 被選擇在
被選擇在  中由
中由  。
。
請注意,分支始終是有限的,因為 tableau 是有限的。幸運的是,對使用哪種選擇函式沒有限制。例如,可以使用一個始終選擇“最左側”分支的選擇函式。
定義 33 (超 Tableau - 基本情況)
[編輯 | 編輯原始碼]設  是一個有限的子句集,而
是一個有限的子句集,而  是一個選擇函式。對於
是一個選擇函式。對於  的超 Tableau 如下所示遞迴定義
的超 Tableau 如下所示遞迴定義
初始化步驟:一個單節點文字樹是  的超 Tableau。它的單個分支標記為“開啟”。
的超 Tableau。它的單個分支標記為“開啟”。
超擴充套件步驟:如果
 是
是  的一個開放超 Tableau,
的一個開放超 Tableau, (即
(即  被選擇在
被選擇在  中由
中由  )具有開放的葉節點
)具有開放的葉節點  ,並且
,並且 是
是  中的一個子句(
中的一個子句( ,
, ),在此上下文中稱為擴充套件子句,並且
),在此上下文中稱為擴充套件子句,並且- 使得
 (稱為 *超條件*)。
(稱為 *超條件*)。
那麼文字樹 是
是 的超表格,其中
的超表格,其中 是透過將
是透過將 個子節點
個子節點 附加到
附加到 上,並分別用以下標籤標記:
上,並分別用以下標籤標記:

並將每個新的分支 標記為“開啟”,並標記每個新的分支
標記為“開啟”,並標記每個新的分支 標記為“關閉”。
標記為“關閉”。
子句集 顯然有兩個不同的模型:
顯然有兩個不同的模型: 和
和  。在集合包含下,這些模型可以進行比較,在某些任務中,計算最小模型(或一般來說是 *一個* 最小模型)是合適的。例如,以下情況就是如此:
。在集合包含下,這些模型可以進行比較,在某些任務中,計算最小模型(或一般來說是 *一個* 最小模型)是合適的。例如,以下情況就是如此:
- 知識表示、迴圈定義
- 預設否定的基礎(GCWA)
- 應用:演繹資料庫更新、診斷
基本上有兩種不同的方法來計算最小模型。
給定一組地子句 ,這些方法應用一個模型生成過程,例如超表格,它能夠生成所有模型。
,這些方法應用一個模型生成過程,例如超表格,它能夠生成所有模型。
引理 1: 對於每個最小模型  存在一個分支,其文字為
存在一個分支,其文字為  。
。
假設  是來自
是來自  的子句頭部出現的原子集,那麼以下引理成立。
的子句頭部出現的原子集,那麼以下引理成立。
引理 2:  是
是  的最小模型當且僅當
的最小模型當且僅當 
這提供了一種通用方法:生成模型候選者,並使用引理 2 進行測試。
 在我們上面的例子中不是最小模型,因為
在我們上面的例子中不是最小模型,因為  當且僅當
當且僅當  不可滿足,但事實並非如此,因此
不可滿足,但事實並非如此,因此  不對應於最小模型,因此該分支被關閉。
不對應於最小模型,因此該分支被關閉。
 是最小的,因為
是最小的,因為  當且僅當
當且僅當  不可滿足。這是正確的,因此
不可滿足。這是正確的,因此  是最小的,該分支保持開啟狀態。
是最小的,該分支保持開啟狀態。
特性: 健壯性(根據引理 2) 完備性(根據引理 1),空間效率。
例如,我們有集合 

引理: 使用補碼分割時,最左邊的開放分支是  的一個最小模型。
的一個最小模型。
通用方法: 重複:生成最小模型  ,將
,將  新增到
新增到  。 屬性: 由於引理的健全性,完整性與之前相同,可能有指數級的新子句
。 屬性: 由於引理的健全性,完整性與之前相同,可能有指數級的新子句  。
。


































































