計算機科學家邏輯/命題邏輯/預備知識

預備知識

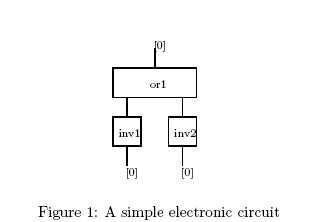
作為一個執行的例子，考慮圖 1 中的簡單數位電路，它包含一個或門 ($or1$) 和兩個反相器 ($inv1$ 和 $inv2$)。系統描述由以下命題公式給出，其中公式按順序標記以方便識別圖 1 中的對應部分。公式中使用的助記符如下

• 符號 $\lor$，$\land$ 和 $\lnot$ 分別表示“或”、“與”和“非”。
• $i1$ 和 $i2$ 表示或門的輸入，$i$ 表示反相器，$o$ 表示門的輸出。
• $high$ 是一個謂詞，它用於表示其引數指定的值“處於高電壓”，即處於開啟狀態。
• $ab$ 是一個謂詞，表示“異常”，即表示式 $\lnot (ab(inv1))$ 可以理解為“反相器一沒有異常”。

$OR1:{\lnot (ab(or1))\to high(or1,o)\leftrightarrow (high(or1,i1)\lor high(or1,i2))}$
$INV1:{\lnot (ab(inv1))\to high(inv1,o)\leftrightarrow \lnot (high(inv1,i))}$
$INV2:{\lnot (ab(inv2))\to high(inv2,o)\leftrightarrow \lnot (high(inv2,i))}$
$CONN1:{high(inv1,o)\leftrightarrow high(or1,i1)}$
$CONN2:{high(inv2,o)\leftrightarrow high(or1,i2)}$

這些公式包含表達其預期含義的標籤：OR1 代表描述或門功能的公式，IN1 和 IN2 描述了兩個反相器（相同）的行為：CONN1 和 CONN2 指定了或門輸入與反相器輸出的連線方式。注意，在此描述中，系統的輸入和輸出尚未定義。從圖形描述中我們可以觀察到，電路的兩個輸入都具有低電壓，輸出也具有低電壓，即我們可以透過公式 $\lnot high(inv1,i),\;\lnot high(inv2,i),\;$ $\lnot high(or1,o)$ 來描述這一點。

此示例演示瞭如何使用諸如 $high(inv1,o)$ 這樣的命題來正式描述電子電路的行為。請注意 $high(inv1,o)$ 可以直觀地理解為“反相器 1 的輸出為高”，當然，這句句子可以透過忽略片語結構並將其理解為一個簡單的字串來進一步簡化：“反相器 1 的輸出為高”。如果我們對其他命題也採用同樣的方式進行處理，我們將得到這樣的公式。

反相器 1 的輸出為高 $\leftrightarrow$ 反相器 1 的輸入為高

此公式包含兩個透過雙箭頭連線的命題。可以很容易地看出，這種方式會導致公式變得很長，因此我們可以透過更簡單的字串（例如 $P_{1}$ 或 $P_{2}$）來進一步縮寫命題，從而得到公式 $P_{1}\leftrightarrow P_{2}$。透過上述論證應該清楚，對於我們的目的而言，此公式與 $high(or1,i1)\leftrightarrow high(inv1,o)$ 傳達的資訊相同。唯一的區別是，後者與讀者聯絡在一起一些直覺，而對於我們形式邏輯框架而言，這無關緊要，我們將專注於任意命題。

在接下來的內容中，我們將系統地避免在語言設計中引入任何與現實世界含義相關的直覺。我們將專注於研究可以透過我們的語言表達的邏輯方面，而不是某個特定的預期含義。換句話說，我們之前介紹的用於描述玩具電子電路的邏輯公式，過於依賴於由圖片引發的解釋。

我們將透過一個非常簡單的歸納定義來介紹命題邏輯的語法，然後透過另一個單獨的定義來指定形式語義。