楓葉/與相對論相關的方程繪圖

變數賦值和繪圖都是簡單的楓葉函式，它們非常重要，可以用於各種目標，無論是為使方程式更容易使用而為物理常量賦值，還是使對 1000 個項的資料集進行繪圖的任務更加易於管理。在這裡，我們將使用與狹義相對論相關的方程式來演示這些簡單的命令。

繪製 e=mc^2 影像

E=mc^2 是一個非常著名的方程式，它描述了能量和質量之間的關係。完整的方程式包含一個伽馬函式，它根據速度基本修改了答案。該圖表明，當速度接近光速時，能量接近無窮大。

1. 將 c 賦值為 1。（儘管光速 'c' 在狹義相對論中實際上接近 3*10^8 m/s，但我們使用將它設為 1 的約定，這樣當我們使用非常大的速度時，我們可以將它們賦值為光速的幾分之一。例如，v=0.5 是光速的一半）

2. 賦值函式： $\gamma (v)={\frac {1}{\sqrt {1-v^{2}/c^{2}}}}$

3. 賦值函式： $E(v,m)=\gamma (v)\,m\,{c}^{2}$

4. 在 m= 0 到 0.9 的範圍內繪製 E(v,30) 影像。為了標記 y 軸，請在 maple 繪圖命令中將您想要的標籤作為第三個項輸入，在指定範圍之後。參見下文。另請參見如何新增標題。

解決方案（楓葉命令）

c:=1;
Gamma:= (v)-> 1/sqrt(1-(v**2/c**2));
E:= (v,m)-> Gamma(v) * m * c**2;
plot(E(v,30), v=0..0.9, energy, title="Energy Mass Relationship");

繪製長度收縮方程影像

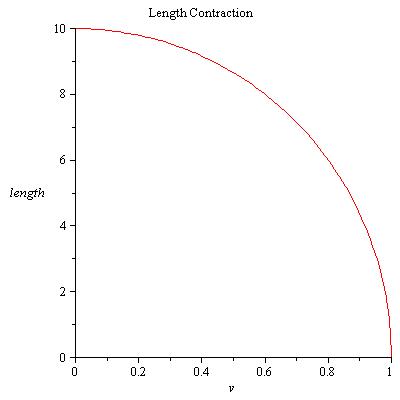
狹義相對論理論解釋了，從另一個參考系觀察到的物體的長度在其沿長度方向運動時會收縮。實際上，當物體的相對速度接近光速時，物體的長度接近零。從理論上講，物體永遠不會真正達到光速。此方程式為 L_prime= L/Gamma。 L_prime 是收縮後的長度，L 是 '固有長度' 或在物體參考系中測量的長度。 Gamma 是上面的問題。繪製一輛 10 米長的轎車從 v=0 到 c 的 L_prime 影像。

解決方案

c:=1;
Gamma:= (v)-> 1/sqrt(1-(v**2/c**2));
L_prime:= (L,v)-> L/Gamma(v);
plot(L_prime(10,v),v=0..c, length, title="Length Contraction");

計算日常物體長度收縮

伽馬在這些方程式中的作用本質上是修正因子，用於考慮不同值相對於物體運動速度的變化。長度變化不會影響我們的日常生活，因為我們周圍的一切物體運動速度都太慢，無法影響我們感知的長度或時間。為了證明這一點，嘗試將不同的速度代入 1 米長的物體的 L_prime 方程式，看看行人速度（約 1.5 m/s）、汽車速度（約 30 m/s）、X-43 火箭/超燃衝壓發動機飛機速度（3,111 m/s）以及阿波羅 10 號重返大氣層時的實際速度的 10,000 倍（11,100 m/s * 10,000）會產生多大的變化。使用光速的實際值作為 c，即 299,792,458 m/s。（透過使用 evalf 函式，它強制 maple 輸出小數而不是繁瑣的分數）。注意，即使在非常高的宇宙飛船速度下，變化也很小。

解決方案

L_prime:= (L,v)-> L/Gamma(v);
c:=299792458;
evalf(L_prime(1,1.5));
                                                           1.000000000
evalf(L_prime(1,30));
                                                           0.999999999
evalf(L_prime(1,3111));
                                                           0.999999999
evalf(L_prime(1,(11,100*10000)));
                                                           0.9290317539

可以看出，在我們能夠達到的速度下，長度收縮可以忽略不計。速度
行走 - 1 米
汽車 - 1 米
飛機 - 1 米
阿波羅 10 號的 10,000 倍 - 0.93 米

相對論中的動能（每個圖繪製多個函式）

對於日常情況，我們可以使用方程式 $E={\frac {m\,v^{2}}{2}}$ 來根據物體的質量和速度測量物體的動能。然而，狹義相對論告訴我們，當速度接近光速時，能量會增加到無窮大。更精確的方程式描述了非常高的相對速度下的動能，即 $E=\lambda \,m\,c^{2}-m\,c^{2}$ 。賦值這兩個函式，然後將它們一起繪製在同一個圖上，以顯示牛頓動能方程式 (E=mv^2/2) 在非常高的速度下的誤差。以光速的 10%、50% 和 100% 繪製這兩個方程式的影像。請注意，直到非常高的速度，在兩個方程式中計算出的能量的差異都可以忽略不計。

解決方案

kinetic:=(m,v)-> (1/2)*m*v**2; 

kinetic2:= (m,v)-> Gamma(v) * m * c**2- m*c**2; 

c:= 299792458; 

plot([kinetic2(13, v), kinetic (13,v)], v=0..(.1*c),kinetic_energy, title="Difference Between Newtonian and Relativistic Kinetic Energies at 10% c");

plot([kinetic2(13, v), kinetic (13,v)], v=0..(.5*c),kinetic_energy, title="Difference Between Newtonian and Relativistic Kinetic Energies at 50% c");

plot([kinetic2(13, v), kinetic (13,v)], v=0..c,kinetic_energy, title="Difference Between Newtonian and Relativistic Kinetic Energies at 100% c");