物理數學方法/一般理論

對於線性運算元$L$在$\mathbb {R}$上的格林函式是一個實函式$g$，使得$Lx=y$的解為$x=g*y$；其中$*$表示卷積。因此，$L(g*y)=y$，使得$g*y$是$L$的右逆，而$g*$是非齊次方程的特定解。

例如：$({\tfrac {d}{dt}})^{2}x+x=f$的解為$x=\sin *f=\int _{0}^{t}sin(t-\tau )f(\tau )d\tau$

這樣的函式可能不存在，即使存在也可能不唯一。這種方法有效的條件需要仔細研究。然而，格林函數理論在分佈理論或廣義函數理論中獲得了更完整和更正則的形式。

正如我們將看到的，格林函數理論提供瞭解微分方程的極其優雅的方法。我們希望在此以嚴格的基礎介紹這種方法。

狄拉克δ函式

狄拉克δ函式$\delta (x)$不是通常定義的函式。然而，我們把它寫成函式一樣，記住定義的範圍。

對於任何函式$f:\mathbb {R} \to \mathbb {R}$，我們定義

$\int _{-\infty }^{\infty }f(x)\delta (x)dx=f(0)$ 但對於每個 $\epsilon >0$,

$\int _{-\infty }^{-\epsilon }f(x)\delta (x)dx=\int _{\epsilon }^{\infty }f(x)\delta (x)dx=0$

由此可知 $\int _{-\infty }^{\infty }\delta (x)dx=1$

這些條件似乎滿足了一個“函式” $\delta (x)$，當 $x\neq 0$ 時其值為零，但在 $x=0$ 時其值為“無窮大”。

近似

有幾種方法可以用普通函式的序列來近似狄拉克函式。我們給出兩個例子。

方波函式

方波函式 $B_{n}:\mathbb {R} \to \{0,n\}$，使得

$B_{n}(x)={\begin{cases}0&|x|>{\tfrac {1}{2n}}\\n&|x|\leq {\tfrac {1}{2n}}\end{cases}}$

我們可以看到，序列 $\left\langle B_{n}\right\rangle$ 代表了對狄拉克函式的近似。

鐘形曲線

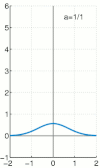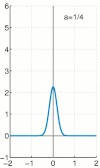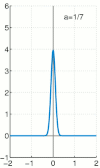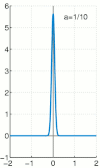
狄拉克函式也可以用無處不在的 高斯函式 來近似。

我們寫 $G_{n}(x)={\frac {n}{\sqrt {\pi }}}\mathrm {e} ^{-x^{2}n^{2}}$

格林函式

考慮一個如下型別的方程 ${\mathcal {L}}u(x)=F(x)$...(1)，其中 ${\mathcal {L}}$ 是一個 *微分運算元*。函式 $u,F$ 通常可能包含多個自變數，但為了清晰起見，這裡我們將其寫成實值函式。在大多數感興趣的情況下，此方程可以寫成

$a(x){\frac {d^{2}u}{dx^{2}}}+b(x){\frac {du}{dx}}+c(x)=F(x)$，需要在某個閉合集 $A$ 上求解 $u(x)$，其中 $a(x)$ 在 $A$ 上不為零。

現在，在物理問題中，求解方程 ${\mathcal {L}}u(x)=f(x)$ 更加方便，當 $f$ 是狄拉克函式 $f(x)=\delta (x-x_{0})$。

在這種情況下，運算元 ${\mathcal {L}}$ 的解稱為 **格林函式** $G(x,x_{0})$。也就是說，

${\mathcal {L}}G(x,x_{0})=\delta (x-x_{0})$

現在，根據狄拉克函式的定義，我們有 $F(x)=\int _{-\infty }^{\infty }F(x')\delta (x'-x)dx$，其中 $F(x')$ 充當狄拉克函式的“權重”。

因此，我們有， ${\mathcal {L}}u(x)=\int _{-\infty }^{\infty }F(x'){\mathcal {L}}G(x,x')dx$

請注意這裡${\mathcal {L}}$ 是一個依賴於 $x$ 但不依賴於 $x'$ 的運算元。因此，

${\mathcal {L}}u(x)={\mathcal {L}}\int _{-\infty }^{\infty }F(x')G(x,x')dx$。我們可以將此視為類似於 ${\mathcal {L}}$ 的反演，因此，我們寫成

$u_{p}(x)=\int _{-\infty }^{\infty }F(x')G(x,x')dx$

下標 $p$ 表示我們已經找到了許多可能的解中的一個特定解。例如，考慮任何諧波解 ${\mathcal {L}}u_{h}(x)=0$。

如果我們新增 $u'(x)=u_{h}(x)+u_{p}(x)$，我們看到 $u'(x)$ 仍然是 (1) 的解。因此，我們有一類滿足 (1) 的函式。

邊界值問題

物理問題通常表示為運算元方程 ${\mathcal {L}}u(x)=F(x)$，在閉集 $A$ 上求解 $u$，以及 **邊界條件**，即 $u(x_{b})=u_{b}(x_{b})$ 對於所有 $x_{b}\in \partial A$ （$\partial A$ 是 $A$ 的邊界）。

$u_{b}(x_{b})$ 是一個給定的函式，滿足 ${\mathcal {L}}u_{b}(x)=0$，描述了該區域邊界上解的行為。

因此，如果一個問題被描述為

${\mathcal {L}}u(x)=F(x)$，其中

$u(x_{b})=u_{b}(x_{b})$

需要在閉合集 $A$ 上求解 $u(x)$，

解可以表示為 $u_{S}(x)=u_{p}(x)+u_{b}(x)=\int _{-\infty }^{\infty }F(x')G(x,x')dx+u_{b}(x)$

從本徵函式得到格林函式

考慮微分運算元 ${\mathcal {L}}$ 的本徵值 $\lambda _{n}$ 和對應的本徵函式 $\phi _{n}$，即 ${\mathcal {L}}\phi _{n}=\lambda _{n}\phi _{n}$

不失一般性，我們假設這些本徵函式是正交的。此外，我們假設它們構成一個基。

因此，我們可以寫 $u(x)=\sum _{i=1}^{n}\alpha _{i}\phi _{i}$ 和 $F(x)=\sum _{i=1}^{n}\beta _{i}\phi _{i}$.

現在 ${\mathcal {L}}u(x)={\mathcal {L}}\sum _{i=1}^{n}\alpha _{i}\phi _{i}=\sum _{i=1}^{n}\alpha _{i}{\mathcal {L}}\phi _{i}=\sum _{i=1}^{n}\alpha _{i}\lambda _{i}\phi _{i}=\sum _{i=1}^{n}\beta _{i}\phi _{i}=F(x)$ 因此，$\alpha _{i}={\frac {\beta _{i}}{\lambda _{i}}}$

根據正交性的定義，$\beta _{n}=\int _{-\infty }^{\infty }F(x)\phi _{n}(x)dx=(F(x)\cdot \phi _{n}(x))$

現在，$u(x)=\sum _{i=1}^{n}\alpha _{i}\phi _{i}(x)=\sum _{i=1}^{n}{\frac {\beta _{i}}{\lambda _{i}}}\phi _{i}(x)=\sum _{i=1}^{n}{\frac {(F(x')\cdot \phi _{i}(x'))}{\lambda _{i}}}\phi _{i}$

因此，我們可以將格林函式寫成 $G(x,x')=\sum _{i=1}^{n}{\frac {\phi _{i}(x)\phi _{i}(x')}{\lambda _{i}}}$