奈米技術/半導體奈米結構

導航
<< 上一頁：生產方法概述
>< 主頁：奈米技術
>> 下一頁：金屬奈米結構

---

奈米管

某些化合物能夠形成奈米管，其中管由圓形外殼組成，外殼由單個原子層在圓柱形晶格中組成。碳奈米管是最著名的例子，但其他材料也可以形成奈米管，例如氮化硼、二硫化鉬等。

奈米管也可以透過蝕刻掉殼結構棒的芯來製造，但這樣的管通常會在壁中包含許多原子層，並在側面具有晶面。

碳奈米管

碳奈米管是迷人的奈米結構。石墨中常見的一張石墨烯薄片，但捲成小管而不是平面薄片。

碳奈米管具有獨特的機械效能，如高強度、高剛度和低密度，以及有趣的電子效能。單壁碳奈米管可以是金屬或半導體，具體取決於原子排列。

本節簡要介紹了碳奈米管。有關更廣泛的概述，請讀者參考大量有關碳奈米管的評論文章或書籍。

幾何結構

最簡單的碳奈米管型別僅由一層石墨烯組成，捲成無縫圓柱體，被稱為單壁碳奈米管 (SWCNT)，其典型直徑僅為幾個奈米。更大的直徑奈米管結構是奈米管繩，由許多獨立的平行奈米管組成，緊密排列成六角形晶格，以及多壁碳奈米管 (MWCNT)，由彼此巢狀的幾個同心圓柱體組成。

由使用含鐵催化粒子的 CVD 工藝製成的多壁碳奈米管 (MWCNT) 樣品。MWCNT 粘附在墊子上。

單壁碳奈米管

因此，基本配置是 SWCNT。它的結構最容易被解釋為一個圓柱形管，概念上由單個石墨烯片捲曲而成。二維石墨烯片的六角形結構是由於碳原子的$sp^{2}$ 雜化引起的，該雜化導致三個方向上的平面內$\sigma$ 鍵，這些鍵之間的夾角為 120 度。

奈米管可以透過手性向量$C$ 來描述，該向量可以用石墨烯單位向量${\textbf {a}}_{1}$ 和${\textbf {a}}_{2}$ 表示，如${\textbf {C}}=n{\textbf {a}}_{1}+m{\textbf {a}}_{2}$，其中整數集$(n,m)$ 唯一地標識了納米管。此手性向量或“捲起”向量透過連線兩個晶體學等效位置來描述奈米管周長，即該管透過疊加${\textbf {C}}$ 的兩端而形成。

根據手性角，單壁碳奈米管被定義為鋸齒形管 ($\theta =0deg\leftrightarrow m=0$), 扶手椅形管 ($\theta =30deg\leftrightarrow n=m$), 或手性管 ($0deg<\theta <30deg$).

多壁碳奈米管

MWCNTs 由多個 SWCNTs 組成，它們以同軸幾何形狀排列。每個巢狀殼體的直徑為 $d={\sqrt {3}}a_{C-C}(m^{2}+n^{2}+mn)^{1/2}/\pi$，其中 $a_{C-C}$ 是碳-碳鍵的長度，為 1.42 Å。各個殼體直徑的差異意味著它們的手性不同，因此相鄰殼體通常不共面，這導致殼間相互作用很弱。

MWCNTs 中的殼間間距為 $\sim$ 0.34 nm - 與亂層石墨中的層間間距非常接近

電子結構

SWCNT 的電子結構最容易透過再次考慮單層石墨烯片來描述。二維、六邊形晶格石墨烯片具有二維倒空間和六邊形布里淵區 (BZ)。

該 $\sigma$ 鍵主要負責機械效能，而電子效能主要由 $\pi$ 帶決定。透過緊束縛方法，可以計算這些 $\pi$ 帶的能帶結構

石墨烯是一種零帶隙半導體，它有一個被佔據的 $\pi$ 帶和一個未被佔據的 $\pi ^{*}$ 帶，它們在 BZ 中的六個 $K$ 點處相遇，因此表現出金屬特性，即所謂的半金屬。

透過將石墨烯片概念性地捲起來形成奈米管，施加一個週期性邊界條件，這使得只有平面石墨烯片中某些電子態被允許。這些態由奈米管的幾何結構決定，即由手性向量的索引 $(n,m)$ 決定。允許狀態的波向量落線上性空間中石墨烯 BZ 中的特定直線上。

基於這種方案，可以估計特定的奈米管是金屬的還是半導體的。當允許的狀態包括 $K$ 點時，系統將近似表現為金屬。然而，在 $\pi$ 和 $\pi ^{*}$ 能帶相遇，但由於曲率效應略微偏離 $K$ 點，在某些情況下會導致能帶略微開啟

這導致了納米管分類方案，共有三種類型：

• 金屬：這些是扶手椅型奈米管，其中簡併點的微小偏移遠離 $K$ 點不會因對稱性原因導致能帶開啟。

• 小帶隙半導體：這些的特徵是 $n-m=3j$，其中 $j$ 是一個整數。這裡，允許狀態的波矢穿過 $K$ 點，但由於簡併點的微小偏移，會存在一個小的能隙，其大小與奈米管直徑的平方成反比，典型值為幾毫電子伏到幾十毫電子伏之間。

• 半導體：在這種情況下 $n-m\neq 3j$。這會導致更大的能隙，其大小與奈米管直徑成反比： $E_{g}=k/d$，實驗研究表明 $k$ 為 0.7-0.8 eV/nm。

通常，型別 2 奈米管的能隙非常小，以至於它們在室溫下可以被認為是金屬的。據此可以推斷，所有奈米管的 1/3 應該表現出金屬特性，而剩下的 2/3 應該表現出半導體特性。然而，需要注意的是，由於半導體奈米管的能隙與直徑成反比，因此大直徑奈米管在室溫下往往會表現出金屬特性。這在大型 MWCNTs 中尤為重要。

從電學角度來看，MWCNT 可以被視為許多僅弱相互作用的平行導體的複雜結構。由於探測電學性質通常涉及電極接觸最外層殼，因此該殼將主導傳輸性質 。簡單來說，這可以與大直徑 SWCNT 相比，因此通常會表現出金屬行為。

電學和機電性質

許多研究都集中在 SWCNTs 上，以探索奈米管的基本性質。由於其本質上的一維性質和有趣的電子結構，SWCNTs 在低溫下表現出一系列有趣的量子現象

然而，這裡討論的內容目前主要限於室溫性質。

一維導體（如 SWCNT）的電導率 $~G~$ 由朗道爾公式給出

$~G=G_{0}\sum _{i}T_{i}~$,

其中 $~G_{0}=2e^{2}/h=(12.9{\rm {k\Omega )^{-1}}}$；
$~1/G_{0}~$ 是電導量子；
以及 $~T_{i}~$ 是貢獻通道 $~i~$ 的透射係數。

關於奈米管的更多資訊

• 維基百科 碳奈米管
• 奈米管網站
• 碳奈米管屬性的彙總概述

碳奈米管及相關產品的商業供應商

• Nanoledge.com 奈米管及相關產品 - 纖維、顆粒、樹脂和分散體...
• Carbon Solution, Inc. 主要為單壁碳奈米管。
• BuckyUSA 富勒烯、單壁碳奈米管、多壁碳奈米管。
• CNI HiPco 碳奈米管
• Carbolex 單壁碳奈米管，亞克級透過西格瑪奧德里奇銷售
• 西格瑪奧德里奇 單壁碳奈米管

"足球烯"

C₆₀，利用 DFT 計算出的基態電子密度的等值面。

一個 w:足球 是巴克明斯特富勒烯 C₆₀ 的模型。

巴克明斯特富勒烯 (IUPAC 名稱 (C₆₀-I_h)[5,6]富勒烯) 是最小的富勒烯分子，其中沒有兩個五元環共享邊（這可能導致不穩定，如 戊搭烯）。它也是自然界中最常見的，因為它經常存在於 煤煙 中。

C₆₀ 的結構是 截角（T = 3）二十面體，類似於 足球，由 20 個六元環和 12 個五元環組成，每個多邊形的頂點處有一個碳原子，每個多邊形的邊上有一條鍵。

C₆₀ 分子的 w:範德華直徑 約為 1 奈米 (nm)。C₆₀ 分子的核間距離約為 0.7 奈米。

C₆₀ 分子有兩個鍵長。6:6 環鍵（兩個六元環之間）可以被認為是 "雙鍵"，並且比 6:5 鍵（六元環和五元環之間）短。它的平均鍵長為 1.4 埃。

矽足球烯已在金屬離子周圍形成。

硼足球烯

萊斯大學的研究人員預測並描述了一種新型的足球烯，它使用 硼 原子代替通常的碳原子。B-80 結構，每個原子形成 5 或 6 個鍵，預計比 C-60 足球烯更穩定。 研究人員給出的原因之一是，B-80 實際上更像巴克明斯特·富勒推廣的原始測地線圓頂結構，它使用三角形而不是六邊形。然而，這項工作受到了量子化學家的廣泛批評，因為他們得出結論，預測的 Ih 對稱結構在振動上是不穩定的，並且由此產生的籠發生自發對稱性破缺，產生一個具有罕見的 Th 對稱性的起伏籠（排球 的對稱性）。該分子中六原子環的數量為 20，五元環的數量為 12。每個六元環中心都有一個額外的原子，與周圍的每個原子相連。

足球烯的變體

另一種相當常見的巴克明斯特富勒烯是 C₇₀， 但是通常可以獲得具有 72、76、84 甚至高達 100 個碳原子的富勒烯。

在 數學 術語中，富勒烯 的結構是具有五元環和六元環面的 三價 凸 多面體。在 圖論 中，術語 富勒烯 指任何 3- 正則、平面圖，其所有面都為 5 或 6（包括外部面）。由 尤拉多面體公式 |V|-|E|+|F| = 2，（其中 |V|、|E|、|F| 表示頂點、邊和麵的數量）可知，富勒烯中恰好有 12 個五元環和 |V|/2-10 個六元環。

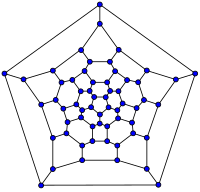
20-富勒烯 （十二面體圖）	26-富勒烯圖	60-富勒烯 （截角二十面體圖）	70-富勒烯圖

最小的富勒烯是 w:十二面體，即唯一的 C₂₀。沒有 22 個頂點的富勒烯。 富勒烯 C_2n 的數量隨著 n = 12、13、14... 的增加而增加，大致與 n⁹ 成正比。例如，有 1812 個非同構的富勒烯 C₆₀。注意，只有 C₆₀ 的一種形式，巴克明斯特富勒烯又名 w:截角二十面體，沒有相鄰的五元環（最小的這種富勒烯）。為了進一步說明這種增長，有 214,127,713 個非同構的富勒烯 C₂₀₀，其中 15,655,672 個沒有相鄰的五元環。

w:三金屬球 碳奈米材料是由弗吉尼亞理工大學的研究人員發現的，並獨家授權給 w:Luna Innovations。這類新型分子由 80 個碳原子（C80）組成一個球體，該球體包圍著三個金屬原子和一個氮原子的絡合物。這些富勒烯封裝了金屬，使它們屬於被稱為 w:金屬富勒烯 的子集。三金屬球有可能用於診斷（作為安全的成像劑）、治療和有機太陽能電池。

半導體奈米線

半導體奈米線可以用大多數半導體材料和不同的方法制成，主要是化學氣相沉積過程（CVD）的各種變化。

存在許多不同的半導體材料，如果晶格常數不太不相容，則可以製成異質結構。由GaAs-GaP等材料組合製成的異質結構可用於在電氣系統中製造電子屏障和導向。

低壓金屬有機物氣相外延（MOVPE）可用於在合適的晶體襯底上外延生長III-V奈米線，例如具有相當匹配晶格常數的III-V材料或矽。

低壓金屬有機物氣相外延（MOVPE）可用於在合適的晶體襯底上外延生長III-V奈米線，例如具有相當匹配晶格常數的III-V材料或矽。奈米線生長由各種奈米顆粒催化，這些奈米顆粒沉積在襯底表面，通常是直徑為20-100nm的金奈米顆粒。

奈米線生長由各種奈米顆粒催化，這些奈米顆粒沉積在襯底表面，通常是直徑為20-100nm的金奈米顆粒。

例如，要生長GaP線，通常將樣品在加熱的反應器室中於650℃退火，以形成金催化劑和下面的襯底之間的共晶。

然後在三甲基鎵和磷化氫的前驅氣體存在下，在約500℃的較低溫度下進行生長。透過在生長過程中改變前驅氣體，可以製成具有不同組成的奈米線異質結構

從催化金奈米顆粒生長的外延奈米線異質結構的SEM影像

資源

• 維基百科 半導體奈米線
• IOFFE 半導體物理性質

奈米顆粒

• 奈米顆粒
• 量子點

催化顆粒

• 催化劑
• 催化
• 哈伯法

奈米顆粒的商業供應商

• Reade 有各種各樣的 奈米顆粒
• sigma-aldrich 有 奈米顆粒分散體
• 奈米相

貢獻者和致謝

• Jakob Kjelstrup Hansen

參考文獻

另請參閱有關如何新增參考文獻的編輯此書籍的說明 Nanotechnology/About#How_to_contribute。

---