數值方法/誤差簡介

當使用數值方法或演算法並使用有限精度進行計算時，會引入近似或舍入和截斷誤差。瞭解它們的性質和階數非常重要。沒有誤差分析，新開發的方法就毫無價值。同樣，使用引入誤差幅度大於要測量或模擬的效應的方法也沒有意義。另一方面，使用精度很高的方法在計算上可能過於昂貴，以至於無法證明其準確性帶來的收益。

準確度和精確度

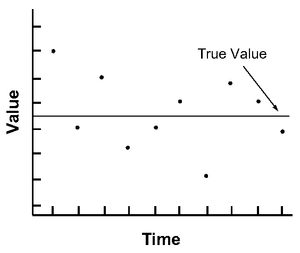
測量和計算可以根據它們的準確度和精確度來描述。準確度是指值與真值之間的一致程度。精確度是指值之間彼此一致的程度。以下圖形說明了準確度和精確度之間的區別。在第一個圖形中，給定值（黑點）更準確；而在第二個圖形中，給定值更精確。術語“誤差”表示數值計算的不精確性和不準確性。

準確度

精確度

絕對誤差

絕對誤差是真值 x 和近似值 xa 之間差值的幅度。因此絕對誤差 = [x-xa] 兩個值之間的誤差定義為

$\epsilon _{abs}=\left\|x-xa\right\|\quad ,$

其中 $x$ 表示精確值，$xa$ 表示近似值。

相對誤差

${\tilde {x}}$ 的相對誤差是絕對誤差相對於精確值的比率。從這個角度來看：如果你的測量誤差為± 1 英寸，當你試圖測量 3 英寸長的東西時，這似乎是一個巨大的誤差。但是，當測量以英里為單位的距離時，此誤差大多可以忽略不計。相對誤差的定義是

$\epsilon _{rel}={\frac {\left\|{\tilde {x}}-x\right\|}{\left\|x\right\|}}\quad .$

誤差來源

在數值計算中，誤差可能由於以下原因而產生

• 截斷誤差

• 舍入誤差

截斷誤差

“截斷”一詞的意思是“縮短”。截斷誤差是指方法中產生的誤差，這種誤差是由於某些數字/步驟序列（有限或無限）被截斷（縮短）為更少的數字而產生的。此類誤差本質上是演算法誤差，我們可以預測方法中將發生的誤差程度。例如，如果我們透過其泰勒級數的前兩個非零項來近似正弦函式，如 $\sin(x)\approx x-{\tfrac {1}{6}}x^{3}$ 對小的 $x$，則由此產生的誤差就是截斷誤差。即使使用無限精度算術，它也存在，因為它是由截斷無限泰勒級數來形成演算法造成的。

舍入誤差

舍入誤差是由於計算裝置無法處理某些數字而產生的。此類數字需要舍入到某個近似值，該近似值取決於裝置用於表示數字的字長。