OPT 設計

輸出變壓器設計基礎

電子管輸出變壓器設計

本書的目的是向世界展示如何設計輸出變壓器或 OPT，以及需要考慮哪些因素。

理論

最基本的考慮因素是磁芯在任何電壓或頻率下都不能發生飽和。這意味著磁芯必須能夠承受

$B={\frac {U_{rms}}{4,44NAf}}[T]$

由於直流電流幾乎總是存在的（尤其是在單端設計中），我們還必須考慮磁場強度 H

$H={\frac {NI}{lm}}[A/m]$

其中 lm 是磁芯周圍的平均磁路長度。

此外，可以證明，初級電感需要從以下事實中得出

$w_{l}L>r_{p}//R_{L}$

其中 RL 是反射負載電阻，rp 是電子管的板極電阻。

這產生了以下公式

$L>(r_{p}//n^{2}Z_{L})/w_{l}$

其中 ZL 是揚聲器標稱阻抗，n 是變壓器的匝數比。

此外，可以證明，當每個電子管的負載為

$R_{L}=2r_{p}$

時，輸出功率最大。

知道了這一點，就可以計算出最小電感 L。

然而，小訊號模型也對方程高頻引數提出了限制。如果 OPT 繞得很仔細（分段繞制，而不是雙線繞制Template:Fix/category，並且每層之間至少有一層變壓器膠帶），主要的高頻問題將是所謂的漏電感。計算它的公式是

$w_{h}L_{leak}<(r_{p}+R_{L})$$w_{h}L_{leak}<(r_{p}+R_{L})$

或

$L_{leak}<(r_{p}+R_{L})/w_{h}$$L_{leak}<(r_{p}+R_{L})/w_{h}$

然而，這個引數很難控制。但經驗表明，一個重要的因素是，次級繞組必須覆蓋整個初級繞組（或兩個初級繞組）。另一個想法是，繞組端點不能摺疊。最後一點主要可以消除高頻諧振。

環形變壓器的電感可以表示為

$L={\frac {\mu _{eff}N^{2}h}{2\pi }}\ln {\frac {b}{a}}[H]$$L={\frac {\mu _{eff}N^{2}h}{2\pi }}\ln {\frac {b}{a}}[H]$

其中

$\mu _{eff}=\mu _{0}{\frac {\mu _{r}}{1+{\frac {lg}{lm}}\mu _{r}}}$$\mu _{eff}=\mu _{0}{\frac {\mu _{r}}{1+{\frac {lg}{lm}}\mu _{r}}}$

其中 lg 是氣隙長度，lm 是平均磁路長度。

$\mu _{eff}=\mu _{0}\mu _{r}$

$L={\frac {\mu _{eff}N^{2}h}{2\pi }}\ln {\frac {b}{a}}[H]$$L={\frac {\mu _{eff}N^{2}h}{2\pi }}\ln {\frac {b}{a}}[H]$

$\mu _{r}$

是鐵的相對磁導率，而

$\mu _{0}$

是真空的磁導率。

實際例子

可以證明，單極低通濾波器的滾降在比fh低三倍的頻率上僅產生-0,5dB的影響。這意味著如果我們想要在最高可聽頻率（20kHz）處獲得-0,5dB，我們需要一個60kHz的fh。

因為

$w_{h}=2\pi f_{h}$

這意味著洩漏電感小於

$L_{leak}<33mH$

如果我們想在推輓式（PP）中使用KT66管，其中rp=2rp(KT66)=2500歐姆。請注意，PP設計中的RL是每個管子負載的4倍。因此，在我們的案例中，最佳板間負載為10k歐姆。

同樣的情況也適用於單極高通濾波器，因此-0.5dB@10Hz的fl為3,3Hz。因此電感需要大於

$L>95H$

如果我們想使用建議的鐵芯尺寸，我們得到

$A=6,25\cdot 10^{-4}[m^{2}]$

和

$l_{m}=0,196[m]$

因為P1+P2需要承受230V@15Hz，而變壓器鐵芯的常見最大磁通密度約為

$B=1,6T$

現在可以使用第一個方程計算匝數。這給出

$N=3453$

將此代入初級電感方程，我們得到

$L=0,041\mu _{r}[H]$

因為我們想在A類推輓式配置中使用OPT，所以我們不必過多考慮由於管子老化和揚聲器阻抗隨頻率變化而產生的直流電流。但是，建議OPT應該能夠承受至少透過兩個初級的10mADC直流電流。在SE配置中，需要所謂的空氣隙，但這在環形變壓器中無法（輕易）實現，這使我們依賴於所用鐵芯的BH環路的寬度。

對於我們變壓器中10mA的直流電流，磁場強度為

$H=176[A/m]$

我們希望至少剩下L/3=30H。

方程推導

本段將解釋上述使用方程的推導。

標準OPT使用

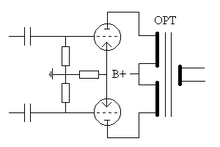標準OPT使用

這張圖片展示了OPT在推輓式（PP）配置中的使用方式。但是，下面的理論也適用於單端式（SE）配置。

OPT小訊號模型

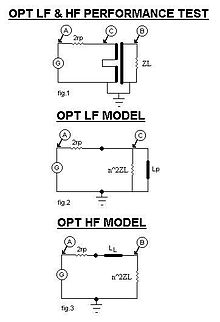OPT小訊號模型

這張圖片展示了OPT的小訊號模型。

圖1顯示了簡單的OPT連線，即透過兩個板極電阻rp（由於PP）由訊號發生器G驅動。

圖2顯示了在低頻下發生的情況，此時OPT作為普通變壓器工作。因此，反射阻抗為

$R_{L}=n^{2}Z_{L}$

其中 n 是 OPT 的匝數比，ZL 是揚聲器的阻抗。

圖 3 顯示了在高頻情況下發生的情況，其中漏 inductance LL 由於前面提到的特殊繞線技術而占主導地位，勝過層間電容。上面的表示式仍然成立。

變壓器基礎

考慮一個理想的變壓器，沒有鐵損或銅損。那麼輸出功率將等於輸入功率。

如果您將高壓轉換成低壓，那麼您將在二次側獲得比一次側輸入的電流更大的電流。

所以如果

$Pin=U1\cdot I1$

那麼

$Pout=U2\cdot I2$

並且如果

$U2=U1/n$

那麼可以推匯出

$I2=n\cdot I1$

最後

$U2/I2=1/n^{2}\cdot U1/I1$

$w_{h}L_{leak}<(r_{p}+R_{L})$$w_{h}L_{leak}<(r_{p}+R_{L})$

$U1/I1=n^{2}\cdot U2/I2$

小訊號模型評估

在圖 2 中使用諾頓和戴維寧電路理論時，我們得到

$wL_{p}>(2rp//n^{2}Z_{L})$

然而，在圖 3 中，我們可能只是意識到這樣一個事實，即

$wL_{L}<(2rp+n^{2}Z_{L})$

因為這是 LL 的 reactance 變得占主導地位的地方。

標準濾波器特性

想象一個單極高通濾波器。那麼你可能有一個與接地電阻串聯的電容器。然後拉普拉斯傳遞函式得出

$Uo/Uin=R/(R+1/sC)$

或者簡化為

$Uo/Uin=1/(1+1/(sRC))$

將

$w_{0}=1/RC$

我們得到

$Uo/Uin=1/(1+w_{0}/s)$

將 s=jw，我們得到

$Uo/Uin=1/(1+w_{0}/jw)$

並且傳遞函式的幅度變為

$Uo/Uin=1/{\sqrt {1+(w_{0}/w)^{2}}}$

$w_{h}L_{leak}<(r_{p}+R_{L})$$w_{h}L_{leak}<(r_{p}+R_{L})$

$Uo/Uin=1/{\sqrt {1+(f_{0}/f)^{2}}}$

其中 f 是頻率。

將

$f=3f_{0}$

我們得到

$Uo/Uin=-0,46dB$

場磁學

在本段中，我們將向世界展示電磁學的基本原理。

麥克斯韋方程組

麥克斯韋方程組的標準形式為

$\nabla \cdot \mathbf {D} =\rho _{f}$

$\nabla \cdot \mathbf {B} =0$

$\nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}$

$\nabla \times \mathbf {H} =\mathbf {J} _{f}+{\frac {\partial \mathbf {D} }{\partial t}}$

第一個方程式，即高斯定律，描述了電荷是如何產生電場的。

第二個方程式指出，不存在“磁荷”，即所謂的磁單極子。

第三個方程式，即法拉第定律，描述了磁場變化是如何產生電場的。

第四個方程式，即安培定律（含麥克斯韋修正項），描述了電場變化是如何產生磁場的。

已用量列表

E : 電場強度 [V/m]

D : 電通量密度 [As/m^2]

H : 磁場強度 [A/m]

B : 磁通量密度 [Vs/m^2]

J_f : 自由電流密度 [A/m^2]

積分形式

$\oint _{S}\mathbf {D} \cdot d\mathbf {s} =\int _{V}\rho _{f}dv$

$\oint _{S}\mathbf {B} \cdot d\mathbf {s} =0$

$\oint _{C}\mathbf {E} \cdot dl=-\int _{S}{\partial \mathbf {B} \over \partial t}\cdot d\mathbf {s}$

$\oint _{C}\mathbf {H} \cdot dl=\int _{S}\mathbf {J} _{f}\cdot d\mathbf {s} +\int _{S}{\partial \mathbf {D} \over \partial t}\cdot d\mathbf {s}$

邊界條件

從介質 1 到介質 2 麥克斯韋方程組給出

$\mathbf {\hat {n}} \cdot (\mathbf {D} _{2}-\mathbf {D} _{1})=\sigma _{f}$

$\mathbf {\hat {n}} \times (\mathbf {E} _{2}-\mathbf {E} _{1})=0{\mbox{ or }}\mathbf {E} _{2t}=\mathbf {E} _{1t}$

$\mathbf {\hat {n}} \cdot (\mathbf {B} _{2}-\mathbf {B} _{1})=0$

$\mathbf {\hat {n}} \times (\mathbf {H} _{2}-\mathbf {H} _{1})=\mathbf {K} _{f}{\mbox{ or }}\mathbf {H} _{2t}-\mathbf {H} _{1t}=\mathbf {K} _{f}\times \mathbf {\hat {n}}$

$L={\frac {\mu _{eff}N^{2}h}{2\pi }}\ln {\frac {b}{a}}[H]$$L={\frac {\mu _{eff}N^{2}h}{2\pi }}\ln {\frac {b}{a}}[H]$

$\sigma _{f}$ 是表面電荷密度，K_f 是介質間的自由表面電流強度。

法拉第定律

考慮法拉第定律，我們從麥克斯韋方程組中得到

$\oint _{C}Edl=-{\frac {d}{dt}}\int _{S}BdS$

如果我們定義

$V=\oint _{C}Edl$=在曲率 C 上感應的電動勢 [伏特]

和

$\Phi =\int _{S}BdS$=穿過表面 S 的磁通量 [伏秒或韋伯]

那麼我們得到

$V=-{\frac {d\Phi }{dt}}$ [伏特]

如果我們使用幾匝 N 的線圈，我們將得到

$V=-N{\frac {d\Phi }{dt}}$ [伏特]

如果磁通量流經鐵芯，其中

$\mu _{r}>>1$

磁通量將只停留在鐵芯中，產生與匝數比 n 成正比的二次電壓。

鐵芯中的磁通密度

根據法拉第定律，我們有

$\Phi =\int _{S}BdS$

由於表面 S 沒有變化，我們有

$\Phi =BS$

使用方程式

$V=-N{\frac {d\Phi }{dt}}$

然後我們得到

$V=-NS{\frac {dB}{dt}}$

正弦磁通密度產生

$B=B_{max}\cdot sin(wt)$

因此

$V=-NSB_{max}\cdot w\cdot cos(wt)$

當發生最大值時

$V=NSB_{max}w$

因此

$B_{max}={\frac {V}{NSw}}$

$w_{h}L_{leak}<(r_{p}+R_{L})$$w_{h}L_{leak}<(r_{p}+R_{L})$

$B_{max}={\frac {V}{2\pi NAf}}$

其中 A 已替代 S

如果電壓是正弦波

$V={\sqrt {2}}V_{rms}$

我們得到

$B_{max}={\frac {V_{rms}}{4,44NAf}}$

鐵芯中的磁場強度

根據麥克斯韋方程組，我們得到

$\oint _{C}\mathbf {H} \cdot dl=NJ_{f}S=NI$

因為我們只考慮直流和均勻表面。

所以如果我們使用環形磁芯，那麼

$H2\pi r=NI$

並且如果

$l_{m}=2\pi r$

那麼

$H={\frac {NI}{l_{m}}}$

氣隙導致的有效磁導率

再次應用安培環路定律，我們得到

$\oint _{C}\mathbf {H} \cdot dl=NI$

這裡我們也有

$B_{f}=B_{g}$

但在磁芯中，我們會有

$H_{f}=B_{f}/\mu$

而在氣隙中

$H_{g}=B_{f}/\mu _{0}$

這給出

${\frac {B_{f}}{\mu }}(2\pi r-lg)+{\frac {B_{f}}{\mu _{0}}}l_{g}=NI$

這可以改寫為

${\frac {B_{f}}{\mu _{0}}}({\frac {lm}{\mu _{r}}}+l_{g})=NI$

$w_{h}L_{leak}<(r_{p}+R_{L})$$w_{h}L_{leak}<(r_{p}+R_{L})$

${\frac {B_{f}}{\mu _{eff}}}l_{m}=NI$

$L={\frac {\mu _{eff}N^{2}h}{2\pi }}\ln {\frac {b}{a}}[H]$$L={\frac {\mu _{eff}N^{2}h}{2\pi }}\ln {\frac {b}{a}}[H]$

$l_{m}=2\pi r-lg$

這給出

$\mu _{eff}=\mu _{0}{\frac {l_{m}}{{\frac {l_{m}}{\mu _{r}}}+l_{g}}}$

$w_{h}L_{leak}<(r_{p}+R_{L})$$w_{h}L_{leak}<(r_{p}+R_{L})$

$\mu _{eff}=\mu _{0}{\frac {\mu _{r}}{1+{\frac {l_{g}}{l_{m}}}\mu _{r}}}$

環形磁芯電感

考慮柱座標系。然後我們得到

$B=a_{\phi }B_{\phi }$

$dl=a_{\phi }rd{\phi }$

$\oint _{C}B\cdot dl=\int _{0}^{2\pi }B_{\phi }rd\phi =2\pi rB_{\phi }$

由於路徑包圍了總電流 NI，因此我們有

$2\pi rB_{\phi }=\mu _{eff}NI$

知道關係

$B=\mu H$

很容易與之前的等式聯絡起來，因此

$B_{\phi }={\frac {\mu _{eff}NI}{2\pi r}}$

和

$\Phi =\int _{S}Bds=\int _{S}a_{\phi }{\frac {\mu _{eff}NI}{2\pi r}}\cdot a_{\phi }hdr$

等於

$\Phi ={\frac {\mu _{eff}NIh}{2\pi }}\int _{a}^{b}{\frac {dr}{r}}={\frac {\mu _{eff}NIh}{2\pi }}\ln {\frac {b}{a}}$

使用磁通鏈為

$N\Phi$

並且小訊號電感獨立於電流，我們得到

$L={\frac {\mu _{eff}N^{2}h}{2\pi }}ln{\frac {b}{a}}$

C 型鐵芯電感

這個不容易計算，但如果我們可以透過以下方式定義平均磁路長度，我們可以做一些近似

$lm=2\cdot c+2\cdot d$

其中 c 是最短邊（在鐵芯中心）和 d 是最長邊。

將此近似為圓形環形形狀，我們得到

$r_{mean}={\frac {lm}{2\pi }}$

在此基礎上加上鐵芯厚度的一半得到 b，減去鐵芯厚度的一半得到 a。然後我們可以重複使用

$L={\frac {\mu _{eff}N^{2}h}{2\pi }}ln{\frac {b}{a}}$

這應該相當有效，因為磁通由於以下原因而保留在鐵芯中

$\mu _{r_{e}ff}>>1$

最佳化管放大器負載

三極體的最大可用功率

如果我們考慮

$i(t)=i_{a}*sin(wt)$

$u(t)=u_{a}*sin(wt)$

並認識到

$i_{a}=I_{a}$

$u_{a}=U_{a}-2R_{i}I_{a}$

輸出功率可以寫成

$P=u_{a}*i_{a}/2=U_{a}I_{a}/2-R_{i}I_{a}^{2}$

並對 Ia 求導得到

${\frac {dP}{dI_{a}}}=U_{a}/2-2R_{i}I_{a}=0$

最大值為

$I_{a}={\frac {U_{a}}{4R_{i}}}$

因此

$P_{max}={\frac {U_{a}^{2}}{8R_{i}}}-{\frac {U_{a}^{2}}{16R_{i}}}={\frac {U_{a}^{2}}{16Ri}}$

從圖中可以看出

$U_{a}=2R_{i}I_{a}+R_{a}I_{a}=I_{a}(2R_{i}+R_{a})={\frac {U_{a}}{4R_{i}}}*(2R_{i}+R_{a})$

其中 Ua 被消去，因此

$1=1/2+{\frac {R_{a}}{4R_{i}}}$

$w_{h}L_{leak}<(r_{p}+R_{L})$$w_{h}L_{leak}<(r_{p}+R_{L})$

$2=1+{\frac {R_{a}}{2R_{i}}}$

因此

$2R_{i}=R_{a}$

證明這一點的更簡單方法是透過觀察影像

$u_{a}=U_{a}-2R_{i}I_{a}=U_{a}-R_{a}I_{a}$

這最終證明了三極體的最佳負載是其內部阻抗的兩倍。但是，應該指出的是，板電壓應該是限制因素，對於板耗散成為問題的高電壓，Ra 必須更高。

值得注意的是，在這種情況下，效率只有 25%，我們可以透過代入證明這一點

$P_{a}=U_{a}*I_{a}=U_{a}^{2}/4R_{i}$

其中

$P_{out}=i_{a}*u_{a}/2=I_{a}*(U_{a}-2R_{i}I_{a})/2={\frac {U_{a}}{4R_{i}}}(U_{a}-2R_{i}{\frac {U_{a}}{4R_{i}}})/2={\frac {U_{a}^{2}}{4R_{i}}}(1-1/2)/2$

因此

${\frac {P_{out}}{P_{a}}}=1/4$