二維逆問題/Dirichlet-to-Neumann 對映的核

The continuous analog of the matrix representation of a Dirichlet-to-Neumann operator for a domain  $\Omega$  is its kernel. It is a distribution defined on the Cartesian product of the boundary of the domain w/itself, such that if

$\Lambda f=g,$ 則 $g(\phi )=\int _{\partial \Omega }K(\phi ,\theta )f(\theta )d\theta ,$ 其中 $\phi$ 和 $\theta$ 使用弧長測度引數化邊界。

For the case of the half-plane w/constant unit conductivity the kernel can be calculated explicitly. It's a convolution, because the domain in consideration is shift invariant:

$K(\phi ,\theta )=k(\phi -\theta ),$ 其中 k 是線上的一種分佈。因此，計算簡化為對一個 $\delta _{0}$ -函式在原點的Dirichlet 問題求解，並在邊界線上取外導數。

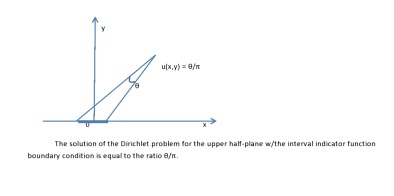
Dirichlet problem for a half-plane — 半平面的 Dirichlet 問題

練習 (**). 完成半平面核 K 的計算，以顯示 $K(x,y)={\frac {-1}{\pi (x-y)^{2}}}$ 不在對角線上。

練習 (*). 證明對於旋轉不變的區域（圓盤，導電率僅取決於半徑），Dirichlet-to-Neumann 對映的核是卷積。

希爾伯特變換給出了調和函式的邊界值與其調和共軛之間的對應關係。 $H:u|_{\partial \Omega }\rightarrow v|_{\partial \Omega },$ 其中 $f(z)=u(z)+iv(z)$ 是域中的解析函式。

對於覆上半平面的情況，希爾伯特變換由以下公式給出： $Hf(y)={\frac {1}{\pi }}\ {\text{p.v.}}\int _{-\infty }^{\infty }{\frac {f(x)}{y-x}}dx.$

練習 (*). 對上述公式進行積分符號求導，得到半平面 Dirichlet-to-Neumann 運算元的核表示。

To define discrete Hilbert transform for a planar network, the network together w/its dual is needed.