OpenGL 程式設計/現代 OpenGL 教程 軌跡球
軌跡球是一種使用滑鼠自然旋轉物體的工具。
想象一個位於屏幕後面的虛擬球。透過用滑鼠點選它,你就可以捏住它,透過移動滑鼠,你可以讓球繞其中心旋轉。相同的旋轉將應用於 OpenGL 場景中的物體!雖然直觀地實現,但事實證明它在使用上並不直觀。
相反,沿著你點選球體的點和當前點之間的方向旋轉,旋轉角度為弧長兩倍,這種方式更容易使用和實現。
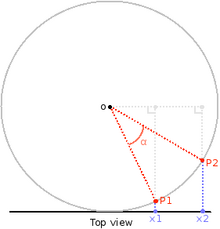
右側的圖示顯示了虛擬球的俯檢視。底部的黑線是螢幕,x1 和 x2 是拖動過程中兩次連續的滑鼠位置。這是在 2D 中顯示的,但相同的原理適用於 3D。
目標是計算 α 角和旋轉軸。當你開始認真使用 OpenGL 時,你會發現數學是必不可少的。我們將用到勾股定理、向量點積和叉積。
我們將
- 將螢幕座標(以畫素為單位)轉換為相機座標(以 [-1, 1] 為單位)
- 計算向量 OP1 和 OP2,它們是與滑鼠點選匹配的球體表面上的點
- x 和 y 座標直接從相機座標中的點選位置獲取
- z 座標使用經典的勾股定理計算
- 如果 P1 或 P2 距離球體太遠(),我們將對其進行歸一化以獲得球體表面上的最近點
- 我們有,球體的大小為 1(),因此我們使用獲取角度。
- 為了獲得 3D 中的旋轉軸,我們計算,它將提供一個單位垂直向量
GLUT 提供了一種獲取滑鼠點選和拖動事件的方法
glutMouseFunc(onMouse) 將為每個滑鼠點選呼叫 onMouse(int button, int state, int x, int y),其中
- button 是 GLUT_LEFT_BUTTON、GLUT_MIDDLE_BUTTON 或 GLUT_RIGHT_BUTTON
- state 是 GLUT_DOWN 或 GLUT_UP
- x 和 y 是螢幕座標,從左上角開始(y 方向與 OpenGL 座標相反!)
glutMotionFunc(onMotion) 將為任何按鈕按下時的每次滑鼠移動呼叫 onMotion(int x, int y),其中 x 和 y 是螢幕座標。
你還可以使用 glutPassiveMotionFunc(...),它在沒有任何按鈕按下時,也能以類似的方式處理滑鼠移動。
因此,我們添加了兩個函式來跟蹤左鍵按下時的滑鼠移動
/* Global */
int last_mx = 0, last_my = 0, cur_mx = 0, cur_my = 0;
int arcball_on = false;
/* main() */
glutMouseFunc(onMouse);
glutMotionFunc(onMotion);
void onMouse(int button, int state, int x, int y) {
if (button == GLUT_LEFT_BUTTON && state == GLUT_DOWN) {
arcball_on = true;
last_mx = cur_mx = x;
last_my = cur_my = y;
} else {
arcball_on = false;
}
}
void onMotion(int x, int y) {
if (arcball_on) { // if left button is pressed
cur_mx = x;
cur_my = y;
}
}
我們添加了一個新的函式來計算軌跡球表面點
/**
* Get a normalized vector from the center of the virtual ball O to a
* point P on the virtual ball surface, such that P is aligned on
* screen's (X,Y) coordinates. If (X,Y) is too far away from the
* sphere, return the nearest point on the virtual ball surface.
*/
glm::vec3 get_arcball_vector(int x, int y) {
glm::vec3 P = glm::vec3(1.0*x/screen_width*2 - 1.0,
1.0*y/screen_height*2 - 1.0,
0);
P.y = -P.y;
float OP_squared = P.x * P.x + P.y * P.y;
if (OP_squared <= 1*1)
P.z = sqrt(1*1 - OP_squared); // Pythagoras
else
P = glm::normalize(P); // nearest point
return P;
}
我們首先將 x,y 螢幕座標轉換為 [-1,1] 座標(並反轉 y 座標)。然後我們使用勾股定理來檢查 OP 向量的長度並計算 z 座標,如上所述。
/* onIdle() */
if (cur_mx != last_mx || cur_my != last_my) {
glm::vec3 va = get_arcball_vector(last_mx, last_my);
glm::vec3 vb = get_arcball_vector( cur_mx, cur_my);
float angle = acos(min(1.0f, glm::dot(va, vb)));
glm::vec3 axis_in_camera_coord = glm::cross(va, vb);
glm::mat3 camera2object = glm::inverse(glm::mat3(transforms[MODE_CAMERA]) * glm::mat3(mesh.object2world));
glm::vec3 axis_in_object_coord = camera2object * axis_in_camera_coord;
mesh.object2world = glm::rotate(mesh.object2world, glm::degrees(angle), axis_in_object_coord);
last_mx = cur_mx;
last_my = cur_my;
}
一旦我們獲得了 OP1 和 OP2(這裡稱為 va 和 vb),我們就可以使用 acos(dot(va,vb)) 計算角度。
由於我們使用的是float變數,可能會出現精度問題:dot可能返回的值略大於1,acos將返回nan,這意味著無效的浮點數。結果是我們的旋轉矩陣將被全部搞亂,通常我們的物體將從螢幕上消失!為了解決這個問題,我們用1.0的最大值限制該值。
另一個技巧是將旋轉軸從相機座標轉換為物體座標。當相機和物體放置不同時,這很有用。例如,如果你在 Y 軸上將物體旋轉 90 度(“將頭部轉向”右側),然後用滑鼠進行垂直移動,你會在相機 X 軸上進行旋轉,但對於物體來說,它應該變成 Z 軸上的旋轉(平面桶式滾動)。透過將軸轉換為物體座標,旋轉將尊重使用者在相機座標系中工作(所見即所得)。為了從相機座標系轉換為物體座標系,我們取 MV 矩陣(來自 MVP 矩陣三元組)的逆矩陣。
最後,我們可以像往常一樣使用glm::rotate應用我們的變換:)
- 旋轉角度是否與滑鼠移動成正比?嘗試在虛擬球體的邊界附近移動。
- 當滑鼠離得太遠時,虛擬球將停止滾動。其他滑鼠控制是可能的。例如,研究在 Blender 3D 建模器中使用中鍵拖動的工作原理。
- 嘗試不同的滾動速度,方法是將旋轉角度相乘。







