OpenSCAD 使用者手冊/示例/Strandbeest

摘要

本章介紹如何使用 OpenSCAD 動畫化像 strandbeest 這樣的複雜機制。

該模型並非用於 3D 列印。

原始碼只是一個檔案，沒有使用外部庫，已在 OpenSCAD 版本 2015.03 中測試。

目標受眾 / 先決條件

您需要安裝 OpenSCAD 並需要了解如何使用 OpenSCAD 的基本知識。

瞭解幾何學的基本知識對於理解如何在紙上構建連桿以及如何使用用於計算連桿的函式至關重要。理解三角學有助於理解函式背後的數學原理，但不是嚴格必需的。

準備

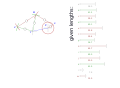
首先，我們需要一個帶有常量的圖紙。

Theo Jansen 在他的網站上釋出了這些數字：[1]（影片“The Legsystem”，3:36）或在網頁的存檔版本上：[2]

我建議給點命名。命名可以是任意的。我使用了 Z..S 來避免與長度 a..m 混淆。

打印出圖紙以方便在上面塗寫可能非常有用。

手工建造

現在我們必須考慮如何手工構建機制。

我們需要一個不可摺疊的圓規、一把尺子、紙和一支鉛筆。

不可摺疊的圓規和尺子

我們將原點 Z 設定為任意點。對於 Y，我們向下 l，向左 a。曲柄 m 可以處於任意角度。繪製曲柄會得到點 X。

從此點開始，我們構造由兩個點和兩個長度定義的三角形。

在幾何學中，這是 SSS 案例（用給定的三條邊構造三角形，另請參見解三角形#給定三條邊（SSS））。

在紙上，這可以使用圓規輕鬆解決。

讓我們首先將圓規設定為長度 b，然後將圓規放在點 Y。然後我們將圓規設定為長度 j，並將圓規放在點 X。圓弧的交點即為點 W。

請注意，當給出兩個點和兩個長度時，總是存在兩個解，即交點。鑑於我們已經知道機制的一般形狀，我們知道我們需要哪一個。但請記住這一點，因為它將在稍後使用。

其餘部分或多或少都是“重複”。

幾何構造說明

約定

長度用小寫字母表示
點用大寫字母表示
用於構造的線和圓弧後面有一個'

說明[編輯 | 編輯原始碼]
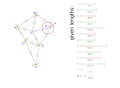
構造點 Z
繪製一條水平線 h
繪製一條垂直線 v，與水平線 h 相交
標記 h 和 v 交點為點 Z

這將是此構造的原點以及腿機構的曲柄軸
構造點 Y
從 h 向下 l 距離繪製一條水平線 h'
從 v 向左 a 距離繪製一條垂直線 v'
標記 h' 和 v' 的交點為固定點 Y
構造點 X
透過 Z 繪製一條線 m'，新增一個任意角度（該角度即為曲柄角度）
從點 Z 以半徑 m 繪製一條圓弧，圓弧 n 和點 Z 的交點即為曲柄樞軸 X

從 Z 繪製一條線 m 到 X
構造點 W（SSS 案例）
從點 X 以半徑 j 繪製一條圓弧 j'
從點 Y 以半徑 b 繪製一條圓弧 b'
圓弧 j' 和 b' 的交點即為點 W

從 X 繪製一條線 j 到 W
從 Y 繪製一條線 b 到 W
構造點 V（SSS 案例）
從點 W 以半徑 e 繪製一條圓弧 e'
從點 Y 以半徑 d 繪製一條圓弧 d'

從 W 繪製一條線 e 到 V
從 Y 繪製一條線 d 到 V
圓弧 e' 和 d' 的交點即為點 V
構造點 U（SSS 案例）
從點 Y 以半徑 c 繪製一條圓弧 c'
從點 X 以半徑 k 繪製一條圓弧 k'

從 Y 繪製一條線 c 到 U
從 X 繪製一條線 k 到 U
圓弧 c' 和 k' 的交點即為點 U
構造點 T（SSS 案例）
從點 V 以半徑 f 繪製一條圓弧 f'
從點 U 以半徑 g 繪製一條圓弧 g'
圓弧 f' 和 g' 的交點即為點 T

從 V 繪製一條線 f 到 T
從 U 繪製一條線 g 到 T
構造點 S（SSS 案例）
從點 T 以半徑 h 繪製一條圓弧 h'
從點 U 以半徑 i 繪製一條圓弧 i'
圓弧 f' 和 g' 的交點即為點 S這是機制的“腳”

從 T 繪製一條線 h 到 S
從 U 繪製一條線 i 到 S

步驟 1
步驟 2
步驟 3
步驟 4
步驟 5
步驟 6
步驟 7
步驟 8

給定長度

    a=38.0
    b=41.5
    c=39.3
    d=40.1
    e=55.8
    f=39.4
    g=36.7
    h=65.7
    i=49.0
    j=50.0
    k=61.9
    l= 7.8
    m=15.0

點

 Z fix point, origin, crank axis
 Y fix point
 X crank axis
 W
 V
 U
 T
 S foot

計算機幾何

要將此轉換為原始碼，我們需要一些幾何函式。

其中大部分是簡單的三角函式。

值得注意的是“atan2”和餘弦定理，在函式 VVLL2D（**V**ector **V**ector **L**ength **L**ength 2D）中實現。

關於 atan2 的所有內容都可以從維基百科中瞭解到：atan2

對於餘弦定理，我推薦這篇文章：http://www.dummies.com/education/math/trigonometry/use-the-law-of-cosines-with-sss/

請記住，對於兩個點和兩個長度，要麼有兩個解，要麼沒有解。目前我們可以忽略沒有解的情況，因為我們知道該機構不會卡住。為了得到方程的另一個解，只需交換引數即可。

繪圖函式

我們還需要一些“繪圖”模組。為了簡單起見，該模組命名為 rod，它只需從一個點畫到另一個點即可。

實現

現在我們有了計算點的幾何函式、一個在兩點之間繪製杆的模組，以及對如何構建物件的總體理解，實現本身出奇地容易。

腿部模組

讓我們看一下腿部模組。

計算程式碼只有八行，繪製杆的程式碼只有十二行。

沙灘獸

對於完整的沙灘獸，我們只需要六條腿，它們之間要有一定的間距和角度偏移。

原始碼

//------------------------
// Trigonometry Functions
//------------------------
function add2D(v1=[0,0],v2=[0,0]) =
    [
        v1[0]+v2[0],
        v1[1]+v2[1]
    ];
  
function sub2D(v1=[0,0],v2=[0,0]) = 
    [
        v1[0]-v2[0], 
        v1[1]-v2[1]
    ];

function addAngle2D(v1=[0,0],ang=0,l=0) = 
    [
        v1[0]+cos(ang)*l,
        v1[1]-sin(ang)*l
    ];

function getAngle2D(v1,v2=[0,0]) =
  atan2(
    (v2[0]-v1[0]), //dx
    (v2[1]-v1[1])  //dy
  );

function scale2D(v1=[0,0],c=1)= 
  [
    v1[0]*c,
    v1[1]*c,
  ];

function length2D(v1,v2=[0,0])=
  sqrt(
      (v1[0]-v2[0])*(v1[0]-v2[0])
      +
      (v1[1]-v2[1])*(v1[1]-v2[1])
    );

//Law of cosines
function VVLL2D(v1,v2,l1,l2) =
  let(sAB = length2D(v1,v2))
  let(ang12=getAngle2D(v2,v1))
  let(ang0=
        acos(
          (l2*l2-l1*l1-sAB*sAB)/
          (-abs(2*sAB*l1))
        ))
        
  addAngle2D(
    v1=v1,
    ang=ang0+ang12-90,
    l=-l1
  );

//----------------------
// modules (Graphic Functions)
//----------------------
// draw "rod" from v1 to v2 with thickness t
module rod(v1=[0,0],v2=[0,0],t=6){
		ang1=getAngle2D(v1,v2);
    len1=length2D(v1,v2);
		translate([v1[0],v1[1]])
		rotate([0,0,-ang1]){
			translate([0,0,0]){
					cylinder(r=t,h=t+2,center = true);
			}
			translate([-t/2,0,-t/2]){
				cube([t,len1,t]);
			}
		}
}

//----------------------
// Leg Module // Jansen mechanism
//----------------------
module leg (
    ang=0,
    a=38.0, //a..m Theo Jansens Constants
    b=41.5,
    c=39.3,
    d=40.1,
    e=55.8,
    f=39.4,
    g=36.7,
    h=65.7,
    i=49.0,
    j=50.0,
    k=61.9,
    l= 7.8,
    m=15.0
    )
{
  Z = [0,0]; //Origin
  X = addAngle2D(Z,ang,m); //Crank / "backbone"
  Y = add2D(Z,[a,l]);
  W = VVLL2D(X,Y,j,b);
  V = VVLL2D(W,Y,e,d);
  U = VVLL2D(Y,X,c,k);
  T = VVLL2D(V,U,f,g);
  S = VVLL2D(T,U,h,i); //Foot
   
  rod(Z, X);
  rod(X, W);

  rod(W, Y);
  rod(W, V);
  rod(Y, V);
  rod(X, U);
  rod(Y, U);
  rod(U, T);
  rod(V, T);
  rod(U, S);
  rod(T, S);
  rod(Z, Y);

  //draw the foot point
  translate(S){
    cylinder(r=8,h=8,center = true); 
  }
}

//----------------------
// Strandbeest
//----------------------
module Strandbeest(ang=$t*360,o=360/3,sgap=20,mgap=50)
{
    {
        color([1, 0, 0]) translate([0,0,sgap*0]) leg(ang+o*0);
        color([0, 1, 0]) translate([0,0,sgap*1]) leg(ang+o*1);
        color([0, 0, 1]) translate([0,0,sgap*2]) leg(ang+o*2);
    }
    mirror(v= [1, 0, 0] ){
        color([1, 0, 0]) translate([0,0,sgap*0]) leg(180-ang-o*0);
        color([0, 1, 0]) translate([0,0,sgap*1]) leg(180-ang-o*1);
        color([0, 0, 1]) translate([0,0,sgap*2]) leg(180-ang-o*2);
    }
    translate([0,0,sgap*2 + mgap])
    {
        color([1, 0, 0]) translate([0,0,sgap*0]) leg(180+ang+o*0);
        color([0, 1, 0]) translate([0,0,sgap*1]) leg(180+ang+o*1);
        color([0, 0, 1]) translate([0,0,sgap*2]) leg(180+ang+o*2);
    }
    translate([0,0,sgap*2 + mgap])   
    mirror(v= [1, 0, 0] ){
        color([1, 0, 0]) translate([0,0,sgap*0]) leg(0-ang-o*0);
        color([0, 1, 0]) translate([0,0,sgap*1]) leg(0-ang-o*1);
        color([0, 0, 1]) translate([0,0,sgap*2]) leg(0-ang-o*2);
    }
}

//leg(ang=$t*360);

rotate([90,180,0]) Strandbeest();

匯出動畫

OpenSCAD 可以將動畫幀匯出為 PNG 檔案。在 Linux 下，可以使用命令列將這些 PNG 檔案轉換為 gif。

convert -delay 10 -loop 0 *.png myimage.gif

Convert 是 ImageMagick 的一部分。

然後可以使用 GIMP 對生成的 GIF 進行裁剪（如果需要）。

接下來，在使用此示例時

我建議將原始碼分成不同的檔案。一種分割方法是

三角函式
繪圖函式
詹森機構/腿部
沙灘獸

我建議使用“use”。這允許您在每個檔案中包含自檢。

為了美化動畫，您可以繪製連線腿部的軸線，或者新增支撐框架。

如果您有 3D 印表機，您可以修改程式碼，以便連線點可以實際旋轉。

接下來，在使用不同的方法構建機構時

角度錯誤/缺少測量值/傾斜

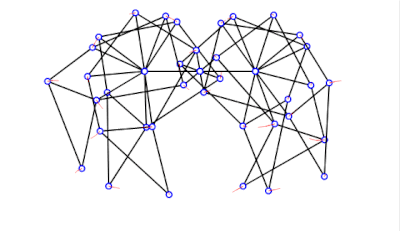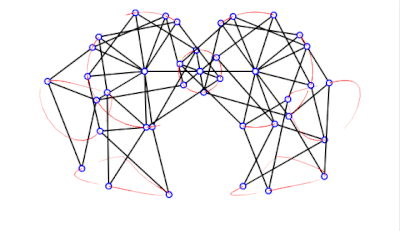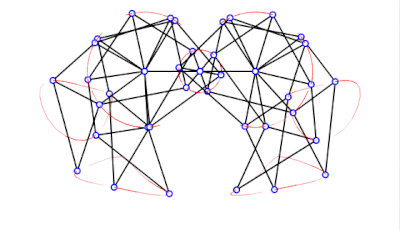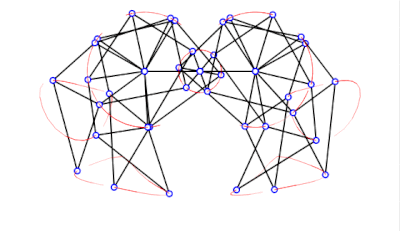
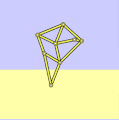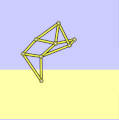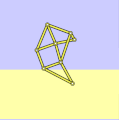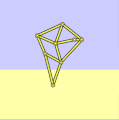
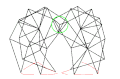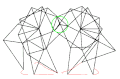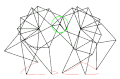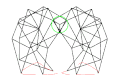
具有正確尺寸的沙灘獸
a = 38.0 l = 7.8
軌跡正確且接地
具有錯誤尺寸的沙灘獸
a = 38.0 l = 0
軌跡提取並傾斜
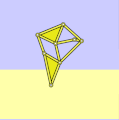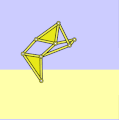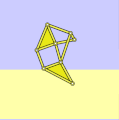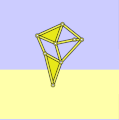
具有錯誤尺寸的沙灘獸
a = 38.79 l = 0
軌跡正確，但傾斜

示例

Klann R&D，Joe Klann，詹森機構 - Klann 機構比較
- https://web.archive.org/web/20160304035711/http://www.mechanicalspider.com/comparison.html
Adam Savage 的一日建造：踏板驅動的沙灘獸！
- https://www.youtube.com/watch?v=G96YQQ7vW8w?t=740
- https://www.youtube.com/watch?v=G96YQQ7vW8w?t=1018

請注意，這些示例並非為了嘲笑創作者的錯誤，而是讚揚他們分享了他們的經驗，以便我們都能從他們那裡學習。

這種錯誤的發生率更高，因為人們說的是十一個^[1]^[2]個神奇數字，而不是 13 個神奇數字。

（有十一根杆，但兩個固定點彼此相距a和l）

三角形

傳統上，腿部只是使用杆形成的。

在使用紙張或木材等平板材料進行製造時，認識到一條腿也可以由 2 個三角形和 5 根杆構成，可以簡化組裝並使機構更加堅固。

以下是一些實際示例

用紙板製成的腿部機構
迷你沙灘獸

準備 3D 列印的模型

一個在 OpenSCAD 中實現的全引數化沙灘獸，包括組裝說明，可用於 3D 列印。^[3]

使用相同長度的杆

f=39,4 和 c=39,3 的長度非常接近，因此使用相同長度的杆可以簡化組裝，而不會對步態造成太大影響。

請注意，在實踐中，整個機構都會發生運動和彎曲，地下並非完全平坦，長度和孔洞會存在製造造成的誤差。

參考文獻

↑ https://ethanzuckerman.com/2007/03/08/theo-jansens-strandbeests/
↑ Linda Leinen (26 September 205). "Theo Jansen: Walking on the Mild Side".
↑ A. Matulich (23 May 2020). "Building the Strandbeest".

[1] ttps://ethanzuckerman.com/2007/03/08/theo-jansens-strandbeests/

[2] Linda Leinen (26 September 205). "Theo Jansen: Walking on the Mild Side".

[3] A. Matulich (23 May 2020). "Building the Strandbeest".

[1]

[2]

[3]