OpenSCAD 使用者手冊/基本實體

立方體

在第一個卦限中建立立方體或長方體（即“盒子”）。當 center 為 true 時，立方體以原點為中心。如果按此處顯示的順序給出，則引數名稱是可選的。

cube(size = [x,y,z], center = true/false);
cube(size =  x ,     center = true/false);

引數:

尺寸

單個值，所有邊長都為該長度的立方體

3 值陣列 [x,y,z]，尺寸為 x、y 和 z 的長方體。

中心

false（預設），第 1（正）卦限，一個角在 (0,0,0)

true，立方體以 (0,0,0) 為中心

default values:  cube();   yields:  cube(size = [1, 1, 1], center = false);

示例:

equivalent scripts for this example
 cube(size = 18);
 cube(18);
 cube([18,18,18]);
 .
 cube(18,false);
 cube([18,18,18],false);
 cube([18,18,18],center=false);
 cube(size = [18,18,18], center = false);
 cube(center = false,size = [18,18,18] );

equivalent scripts for this example
 cube([18,28,8],true);
 box=[18,28,8];cube(box,true);

球體

在座標系的原點建立一個球體。r 引數名稱是可選的。要使用 d 而不是 r，則必須命名 d。

引數

r: 半徑。這是球體的半徑。球體的解析度基於球體的尺寸以及 $fa、$fs 和 $fn 變數。有關這些特殊變數的更多資訊，請參閱：OpenSCAD_User_Manual/Other_Language_Features
d: 直徑。這是球體的直徑。
$fa: 碎片角度（度）
$fs: 碎片尺寸（毫米）
$fn: 解析度

 default values:  sphere();   yields:   sphere($fn = 0, $fa = 12, $fs = 2, r = 1);

使用示例

sphere(r = 1);
sphere(r = 5);
sphere(r = 10);
sphere(d = 2);
sphere(d = 10);
sphere(d = 20);

// this creates a high resolution sphere with a 2mm radius
sphere(2, $fn=100);

// also creates a 2mm high resolution sphere but this one 
// does not have as many small triangles on the poles of the sphere
sphere(2, $fa=5, $fs=0.1);

圓柱體

建立一個以 z 軸為中心的圓柱體或圓錐體。當 center 為 true 時，它也沿 z 軸垂直居中。

如果按此處顯示的順序給出，則引數名稱是可選的。如果命名了一個引數，則所有後續引數也必須命名。

cylinder(h = height, r1 = BottomRadius, r2 = TopRadius, center = true/false);

註釋

如果使用了 r、d、d1 或 d2，則第 2 和第 3 個位置引數為 r1 和 r2，它們必須命名。

使用 r1 和 r2 或 d1 和 d2 且任一值為零將形成圓錐形狀，非零非等值將產生圓錐的一部分（圓錐臺）。r1 和 d1 定義底部的寬度，在 [0,0,0] 處，r2 和 d2 定義頂部的寬度。

引數

h : 圓柱體或圓錐體的高度

r : 圓柱體的半徑。r1 = r2 = r。

r1 : 半徑，圓錐體的底部。

r2 : 半徑，圓錐體的頂部。

d : 圓柱體的直徑。r1 = r2 = d / 2。 [注意：需要版本 2014.03]

d1 : 半徑，圓錐體的底部。r1 = d1 / 2。 [注意：需要版本 2014.03]

d2 : 半徑，圓錐體的頂部。r2 = d2 / 2。 [注意：需要版本 2014.03]

中心

false（預設），z 的範圍從 0 到 h

true，z 的範圍從 -h/2 到 +h/2

$fa : 每個碎片的最小角度（度）。

$fs : 每個碎片的最小周長。

$fn : 360 度中固定的碎片數量。3 或更大的值將覆蓋 $fa 和 $fs

$fa、$fs 和 $fn 必須是命名引數。點選此處瞭解更多詳情。

defaults: cylinder();  yields: cylinder($fn = 0, $fa = 12, $fs = 2, h = 1, r1 = 1, r2 = 1, center = false);

equivalent scripts
 cylinder(h=15, r1=9.5, r2=19.5, center=false);
 cylinder(  15,    9.5,    19.5, false);
 cylinder(  15,    9.5,    19.5);
 cylinder(  15,    9.5, d2=39  );
 cylinder(  15, d1=19,  d2=39  );
 cylinder(  15, d1=19,  r2=19.5);

equivalent scripts
 cylinder(h=15, r1=10, r2=0, center=true);
 cylinder(  15,    10,    0,        true);
 cylinder(h=15, d1=20, d2=0, center=true);

center = false
center = true

equivalent scripts
 cylinder(h=20, r=10, center=true);
 cylinder(  20,   10, 10,true);
 cylinder(  20, d=20, center=true);
 cylinder(  20,r1=10, d2=20, center=true);
 cylinder(  20,r1=10, d2=2*10, center=true);

使用 $fn

較大的 $fn 值可以建立更平滑、更圓的表面，但會延長渲染時間。一些人在開發過程中使用中等值以加快渲染速度，然後在最終的 F6 渲染中將其更改為更大的值。

但是，使用較小的值可能會產生一些有趣的非圓形物體。此處顯示了一些示例

scripts for these examples
 cylinder(20,20,20,$fn=3);
 cylinder(20,20,00,$fn=4);
 cylinder(20,20,10,$fn=4);

尺寸不足的孔

使用 cylinder() 和 difference() 在物體中放置孔會建立尺寸不足的孔。這是因為圓形路徑是用內接於圓的正多邊形來近似的。多邊形的頂點在圓上，但頂點之間的直線在圓內。要使所有孔都大於真實的圓，多邊形必須完全位於圓外（外接）。外接孔的模組

script for this example
 poly_n = 6;
 color("blue") translate([0, 0, 0.02]) linear_extrude(0.1) circle(10, $fn=poly_n);
 color("green") translate([0, 0, 0.01]) linear_extrude(0.1) circle(10, $fn=360);
 color("purple") linear_extrude(0.1) circle(10/cos(180/poly_n), $fn=poly_n);

通常，半徑為 $r$ 的多邊形到任意邊的中點的半徑為 $r_{m}=r\cos(180/n)$ 。如果僅知道中點半徑 $r_{m}$ （例如，將內六角扳手放入六角形孔中），則多邊形半徑為 $r={\frac {r_{m}}{\cos(180/n)}}$ 。

多面體

多面體是最通用的 3D 基本實體。它可用於建立任何規則或不規則形狀，包括具有凹面和凸面特徵的形狀。曲線表面由一系列平面表面近似。

polyhedron( points = [ [X₀, Y₀, Z₀], [X₁, Y₁, Z₁], ... ], triangles = [ [P₀, P₁, P₂], ... ], convexity = N);   // before 2014.03
polyhedron( points = [ [X₀, Y₀, Z₀], [X₁, Y₁, Z₁], ... ], faces = [ [P₀, P₁, P₂, P₃, ...], ... ], convexity = N);   // 2014.03 & later

引數

點

3D 點或頂點的向量。每個點依次是一個向量 [x,y,z]，表示其座標。

可以按任何順序定義點。N 個點按定義的順序引用，從 0 到 N-1。

三角形 [已棄用： 三角形將在未來的版本中移除。請改用面引數]

共同包圍實體的面向量。每個面都是一個向量，包含來自點向量的 3 個點的索引（基於 0）。

面 [注意：需要版本 2014.03]

共同包圍實體的面向量。每個面都是一個向量，包含來自點向量的 3 個或更多點的索引（基於 0）。

可以按任何順序定義面，但每個面的點必須按正確的順序排列（見下文）。定義足夠的面以完全包圍實體，並且沒有重疊。

如果描述單個面的點不在同一平面上，則該面會根據需要自動分割成三角形。

凸度

整數。凸度引數指定與物件相交的光線可能穿過的最大面數。此引數僅在 OpenCSG 預覽模式下正確顯示物件時才需要。它對多面體渲染沒有影響。對於顯示問題，在大多數情況下，將其設定為 10 應該可以正常工作。

 default values: polyhedron(); yields: polyhedron(points = undef, faces = undef, convexity = 1);

在面的列表中，對於每個面，您可以從哪個點開始是任意的，但面的點（透過點列表中的索引引用）必須在從外部向內觀察每個面時按順時針方向排序。背面從背面觀看，底部從底部觀看，等等。記住此排序要求的另一種方法是使用右手定則。使用您的右手，將拇指向上伸出，並像豎起大拇指一樣彎曲手指，將拇指指向面，並按照手指彎曲的方向排序點。在下面的示例中嘗試一下。

示例 1 使用多面體生成 cube( [ 10, 7, 5 ] );



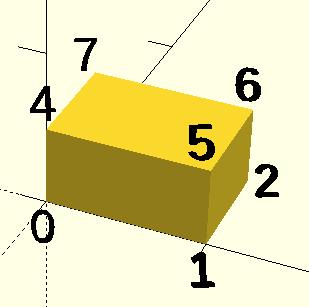
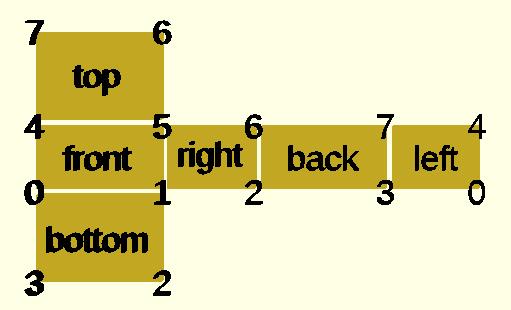
CubePoints = [
  [  0,  0,  0 ],  //0
  [ 10,  0,  0 ],  //1
  [ 10,  7,  0 ],  //2
  [  0,  7,  0 ],  //3
  [  0,  0,  5 ],  //4
  [ 10,  0,  5 ],  //5
  [ 10,  7,  5 ],  //6
  [  0,  7,  5 ]]; //7
  
CubeFaces = [
  [0,1,2,3],  // bottom
  [4,5,1,0],  // front
  [7,6,5,4],  // top
  [5,6,2,1],  // right
  [6,7,3,2],  // back
  [7,4,0,3]]; // left
  
polyhedron( CubePoints, CubeFaces );

equivalent descriptions of the bottom face
  [0,1,2,3],
  [0,1,2,3,0],
  [1,2,3,0],
  [2,3,0,1],
  [3,0,1,2],
  [0,1,2],[2,3,0],   // 2 triangles with no overlap
  [1,2,3],[3,0,1],
  [1,2,3],[0,1,3],

示例 2 方形底座金字塔

polyhedron(
  points=[ [10,10,0],[10,-10,0],[-10,-10,0],[-10,10,0], // the four points at base
           [0,0,10]  ],                                 // the apex point 
  faces=[ [0,1,4],[1,2,4],[2,3,4],[3,0,4],              // each triangle side
              [1,0,3],[2,1,3] ]                         // two triangles for square base
 );

示例 3 三稜柱

注意：此示例中存在錯誤，一個目光銳利的 CAD 工程師注意到展開的三角形不正確，斜邊應為 1,5 和 0,4。正確的展開方式是將它們放在矩形 A 旁邊，沿著邊 1,2 和 0,3。程式碼已更正，希望在不久的將來會出現修訂後的影像。

  module prism(l, w, h){
      polyhedron(//pt 0        1        2        3        4        5
              points=[[0,0,0], [l,0,0], [l,w,0], [0,w,0], [0,w,h], [l,w,h]],
              faces=[[0,1,2,3],[5,4,3,2],[0,4,5,1],[0,3,4],[5,2,1]]
              );
      
      // preview unfolded (do not include in your function
      z = 0.08;
      separation = 2;
      border = .2;
      translate([0,w+separation,0])
          cube([l,w,z]);
      translate([0,w+separation+w+border,0])
          cube([l,h,z]);
      translate([0,w+separation+w+border+h+border,0])
          cube([l,sqrt(w*w+h*h),z]);
      translate([l+border,w+separation,0])
          polyhedron(//pt 0       1       2        3       4       5
                  points=[[0,0,0],[h,w,0],[0,w,0], [0,0,z],[h,w,z],[0,w,z]],
                  faces=[[0,1,2], [3,5,4], [0,3,4,1], [1,4,5,2], [2,5,3,0]]
                  );
      translate([0-border,w+separation,0])
          polyhedron(//pt 0       1         2        3       4         5
                  points=[[0,0,0],[0-h,w,0],[0,w,0], [0,0,z],[0-h,w,z],[0,w,z]],
                  faces=[[1,0,2],[5,3,4],[0,1,4,3],[1,2,5,4],[2,0,3,5]]
                  );
      }
  
  prism(10, 5, 3);

除錯多面體

定義多面體時可能出現的錯誤包括：所有面的頂點順序不都是順時針方向（從外部觀察 - 底面需要從下方觀察），面重疊，以及缺失面或部分面。一般來說，多面體的面也應該滿足流形條件

任何多面體的邊上都應該恰好有兩個面相交。
如果兩個面共用一個頂點，則它們應該在圍繞該頂點的面-邊迴圈中處於相同的迴圈中。

第一條規則消除了諸如兩個共用一條邊的立方體以及非水密模型等多面體；第二條規則排除了諸如兩個共用一個頂點的立方體等多面體。

從外部觀察時，描述每個面的點必須按照相同的順時針順序排列，並提供了一種檢測逆時針方向的方法。當使用 F5 時與 F12 結合使用“組合檢視”時，逆時針方向的面將以粉紅色顯示。重新排列錯誤面的點。旋轉物體以檢視所有面。可以使用 F10 關閉粉紅色檢視。

OpenSCAD 允許暫時註釋掉部分面的描述，以便僅顯示剩餘的面。使用 // 註釋掉該行的其餘部分。使用 /* 和 */ 開始和結束註釋塊。這可以是行的一部分，也可以擴充套件到多行。僅檢視部分面可以幫助確定單個面的正確點。請注意，不會顯示實體，只會顯示面。如果使用 F12，則所有面都有一側為粉紅色。註釋掉一些面也有助於顯示任何內部面。

CubeFaces = [
/* [0,1,2,3],  // bottom
   [4,5,1,0],  // front */
   [7,6,5,4],  // top
/* [5,6,2,1],  // right
   [6,7,3,2],  // back */
   [7,4,0,3]]; // left

定義多面體後，其預覽可能看起來是正確的。多面體本身甚至可能渲染得很好。但是，為了確保它是一個有效的流形並且可以生成有效的 STL 檔案，請將其與任何立方體聯合並渲染（F6）。如果多面體消失了，則表示它不正確。修改所有面的繞序以及上面提到的兩條規則。

面順序錯誤

示例 4 一個具有面順序錯誤的更復雜的多面體

當您從檢視選單中選擇“組合檢視”並編譯（預覽 F5）設計（不要編譯並渲染！）時，預覽會顯示突出顯示的方向錯誤的多邊形。不幸的是，在 OpenCSG 預覽模式下無法進行此突出顯示，因為它會干擾 OpenCSG 預覽模式的實現方式。）

在下面，您可以看到此類有問題多面體的程式碼和圖片，錯誤的多邊形（面或面的組合）以粉紅色顯示。

// Bad polyhedron
polyhedron
    (points = [
	       [0, -10, 60], [0, 10, 60], [0, 10, 0], [0, -10, 0], [60, -10, 60], [60, 10, 60], 
	       [10, -10, 50], [10, 10, 50], [10, 10, 30], [10, -10, 30], [30, -10, 50], [30, 10, 50]
	       ], 
     faces = [
		  [0,2,3],   [0,1,2],  [0,4,5],  [0,5,1],   [5,4,2],  [2,4,3],
                  [6,8,9],  [6,7,8],  [6,10,11], [6,11,7], [10,8,11],
		  [10,9,8], [0,3,9],  [9,0,6], [10,6, 0],  [0,4,10],
                  [3,9,10], [3,10,4], [1,7,11],  [1,11,5], [1,7,8],  
                  [1,8,2],  [2,8,11], [2,11,5]
		  ]
     );

正確多面體如下所示

polyhedron
    (points = [
	       [0, -10, 60], [0, 10, 60], [0, 10, 0], [0, -10, 0], [60, -10, 60], [60, 10, 60], 
	       [10, -10, 50], [10, 10, 50], [10, 10, 30], [10, -10, 30], [30, -10, 50], [30, 10, 50]
	       ], 
     faces = [
		  [0,3,2],  [0,2,1],  [4,0,5],  [5,0,1],  [5,2,4],  [4,2,3],
                  [6,8,9],  [6,7,8],  [6,10,11],[6,11,7], [10,8,11],
		  [10,9,8], [3,0,9],  [9,0,6],  [10,6, 0],[0,4,10],
                  [3,9,10], [3,10,4], [1,7,11], [1,11,5], [1,8,7],  
                  [2,8,1],  [8,2,11], [5,11,2]
		  ]
     );

初學者提示

如果您不完全理解“方向”，請嘗試識別方向錯誤的粉紅色面，然後反轉對點向量的引用的順序，直到您得到正確的結果。例如，在上例中，第三個三角形（[0,4,5]）是錯誤的，我們將其修復為[4,0,5]。請記住，面列表是一個迴圈列表。此外，您可以從“檢視選單”中選擇“顯示邊”，列印螢幕截圖並對點和麵進行編號。在我們的示例中，點以黑色註釋，面以藍色註釋。根據需要旋轉物體並從背面複製第二個副本。這樣您就可以跟蹤。

順時針技術

方向由順時針迴圈索引確定。這意味著如果您從外部觀察三角形（在本例中為 [4,0,5]），您將看到路徑是圍繞面的中心順時針方向的。繞序 [4,0,5] 是順時針方向，因此是正確的。繞序 [0,4,5] 是逆時針方向，因此是錯誤的。同樣，[4,0,5] 的任何其他順時針順序都有效：[5,4,0] 和 [0,5,4] 也都是正確的。如果您使用順時針技術，您的面將始終位於外部（在 OpenSCAD 外部，其他程式使用逆時針方向作為外部）。

將其視為“左手規則”

如果您將左手放在面上，手指彎曲的方向與點的順序相同，則您的拇指應指向外部。如果您的拇指指向內部，則需要反轉繞序。

“多面體”的簡潔描述

點定義形狀中的所有點/頂點。
面是連線點/頂點的多邊形列表。

點列表中的每個點都由一個 3 元組 x、y、z 位置規範定義。點列表中的點會自動從零開始編號，以便在面列表中使用（0、1、2、3……等等）。

面列表中的每個面都透過從點列表中選擇 3 個或更多點（使用點順序號）來定義。

例如，faces=[ [0,1,2] ] 定義了一個從第一個點（點從零開始引用）到第二個點，然後到第三點的三角形。

從外部觀察任何面時，面必須按順時針順序列出所有點。

多面體點列表中的點重複

多面體定義的點列表可能包含重複項。當兩個或多個點的座標相同時，它們被視為同一個多面體頂點。因此，以下多面體

points = [[ 0, 0, 0], [10, 0, 0], [ 0,10, 0],
          [ 0, 0, 0], [10, 0, 0], [ 0,10, 0],
          [ 0,10, 0], [10, 0, 0], [ 0, 0,10],
          [ 0, 0, 0], [ 0, 0,10], [10, 0, 0],
          [ 0, 0, 0], [ 0,10, 0], [ 0, 0,10]];
polyhedron(points, [[0,1,2], [3,4,5], [6,7,8], [9,10,11], [12,13,14]]);

定義與以下相同的四面體

points = [[0,0,0], [0,10,0], [10,0,0], [0,0,10]];
polyhedron(points, [[0,2,1], [0,1,3], [1,2,3], [0,3,2]]);