材料彈性概述/示例問題

示例 1

問題陳述

給定彈性體上的一個點，其應力狀態為${\textstyle {\boldsymbol {\sigma }}}$，確定主應力和原始方向與最大剪應力方向之間的夾角。使用解析方程和莫爾圓作圖法解決此問題。應力以 MPa 為單位給出。

${\boldsymbol {\sigma }}={\begin{pmatrix}72&21&0\\21&32&0\\0&0&0\end{pmatrix}}$

解決方案

我們將透過兩種方法解決此問題。首先使用解析解，然後使用莫爾圓。

解析解

我們有以下方程

${\begin{aligned}\sigma '_{11}={\frac {\sigma _{11}+\sigma _{22}}{2}}+{\frac {\sigma _{11}-\sigma _{22}}{2}}cos\left(2\theta \right)+\sigma _{12}sin\left(2\theta \right)\\\sigma '_{22}={\frac {\sigma _{11}+\sigma _{22}}{2}}-{\frac {\sigma _{11}-\sigma _{22}}{2}}cos\left(2\theta \right)-\sigma _{12}sin\left(2\theta \right)\end{aligned}}$

以及

${\begin{aligned}\sigma '_{12}={\frac {\sigma _{22}-\sigma _{11}}{2}}sin\left(2\theta \right)+\sigma _{12}cos\left(2\theta \right)\end{aligned}}$

其中主應力是在旋轉參考系中。當 $\sigma '_{12}=0$ 時，系統處於其主方向，並且 $\sigma '_{11}=\sigma _{p1}$ 和 $\sigma '_{22}=\sigma _{p2}$。設定 $\sigma '_{12}=0$ 並求解得到

$tan\left(2\theta \right)={\frac {2\sigma _{12}}{\sigma _{22}-\sigma _{11}}}$

並將此題中給出的應力代入，我們發現 $\theta =23.2$°。將這個 $\theta$ 的值和給定的 ${\boldsymbol {\sigma }}$ 值代入，得到 $\sigma '_{11}=\sigma _{p1}=81$ MPa，$\sigma '_{22}=\sigma _{p2}=23$ MPa，以及 $\sigma '_{12}=0$ MPa，這驗證了這確實是主軸。

如果我們給定的應力狀態是主方向，那麼在我們上面旋轉的參考系中，${\boldsymbol {\sigma '}}$ 中的 $\sigma _{12}$ 項為零。我們透過對 $\sigma '_{12}$ 求導，將其設為零，並求解 $\theta$ 來找到最大剪下方向。

${\frac {d\sigma '_{12}}{d\theta }}={\frac {d}{d\theta }}\left({\frac {\sigma _{22}-\sigma _{11}}{2}}sin\left(2\theta \right)\right)=\left(\sigma _{22}-\sigma _{11}\right)cos\left(2\theta \right)$

最大值出現在 $\theta =45$° 時。這意味著最大值或最小值出現在 $23.2+45=68.2$°。將此值代入我們的方程以及 ${\boldsymbol {\sigma }}$ 可以得到 $\sigma '_{11}=\sigma _{p1}=52$ MPa，$\sigma '_{22}=\sigma _{p2}=52$ MPa 和 $\sigma '_{12}=-29$ MPa，也就是最小值。由於系統的對稱性，再旋轉 $90$° 會得到最大值，$\sigma '_{11}=\sigma _{p1}=52$ MPa，$\sigma '_{22}=\sigma _{p2}=52$ MPa 和 $\sigma '_{12}=29$ MPa。

莫爾圓解

該圖展示了該示例問題的莫爾圓表示。

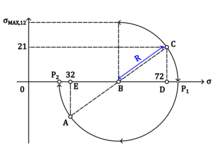
根據這裡給出的圖表，

$Radius=AB=BC={\sqrt {BD^{2}+CD^{2}}}$

以及

$tan\left(2\theta \right)={\frac {CD}{BD}}$

假設 $CD=21$，$OD=72$，以及$OE=32$，我們可以得出結論 $AD=40$ 以及 $EB=BD=20$。因此，$Radius=29$ 以及 $\theta =23.2$°。從主方向 $P1=OB+Radius=OE+EB+Radius=81$ MPa 以及 $P2=P1-2Radius=23$ MPa。最小和最大剪下應力是 $\pm Radius=\pm 29$ MPa，它們可以透過將系統旋轉 $23.2+45=68.2$° 以及 $23.2+45+90=158.2=-21.8^{\circ }$ 來找到。

示例 2

問題陳述

假設彈性體上一點的應力狀態為 ${\textstyle {\boldsymbol {\sigma }}}$，確定主應力。應力單位為 MPa。 [提示：只有一種方法可以繪製莫爾圓圖。利用這一點簡化你的工作。你將會發現，一旦你畫出圖，幾乎就不用進行任何計算了。]

${\boldsymbol {\sigma }}={\begin{pmatrix}0&6&8\\6&0&10\\8&10&0\end{pmatrix}}$

示例 3

問題陳述

假設彈性體上一點的應力狀態為${\textstyle {\boldsymbol {\sigma }}}$，繞${\textstyle x_{3}}$軸旋轉後得到應力狀態${\textstyle {\boldsymbol {\sigma '}}}$，完全確定這兩個應力狀態和未知引數${\textstyle q}$。應力單位為 MPa。

${\boldsymbol {\sigma }}={\begin{pmatrix}25q&\sigma _{12}&0\\\sigma _{21}&5q&0\\0&0&0\end{pmatrix}}~{\boldsymbol {\sigma '}}={\begin{pmatrix}50&5&0\\5&\sigma '_{22}&0\\0&0&0\end{pmatrix}}$

解決方案

圖示了該示例問題的莫爾圓表示法。陰影區域為相似三角形。

我們有以下方程

${\begin{aligned}\sigma '_{11}={\frac {\sigma _{11}+\sigma _{22}}{2}}+{\frac {\sigma _{11}-\sigma _{22}}{2}}cos\left(2\theta \right)+\sigma _{12}sin\left(2\theta \right)\\\sigma '_{22}={\frac {\sigma _{11}+\sigma _{22}}{2}}-{\frac {\sigma _{11}-\sigma _{22}}{2}}cos\left(2\theta \right)-\sigma _{12}sin\left(2\theta \right)\end{aligned}}$

以及

${\begin{aligned}\sigma '_{12}={\frac {\sigma _{22}-\sigma _{11}}{2}}sin\left(2\theta \right)+\sigma _{12}cos\left(2\theta \right)\end{aligned}}$

其中，帶撇的應力表示在旋轉後的參考系中。

利用以上關係，我們就可以代入$\sigma '_{12}$和$\theta$來求得$q=-1/2$。由此可得$\sigma _{11}=-12.5$ MPa 和$\sigma _{22}=-2.5$。不變關係

$\sigma _{11}+\sigma _{22}+\sigma _{33}=I_{1}$

表明

$\sigma _{11}+\sigma _{22}+\sigma _{33}=\sigma '_{11}+\sigma '_{22}+\sigma '_{33}$

透過代入確定$\sigma '_{22}=-65$ MPa。此時，除$\sigma _{12}$外，所有引數都已確定。只需將引數代入$\sigma '_{11}$ 或 $\sigma '_{22}$ 方程，即可求出$\sigma _{12}=57.5$ MPa。最終得到的應力張量（單位為 MPa）為：

${\boldsymbol {\sigma }}={\begin{pmatrix}-12.5&57.5&0\\57.5&-2.5&0\\0&0&0\end{pmatrix}}~{\boldsymbol {\sigma '}}={\begin{pmatrix}50&5&0\\5&-65&0\\0&0&0\end{pmatrix}}$

該解的莫爾圓表示如圖所示。注意，陰影三角形是相似的，因此如果需要圖形求解，可以使用它們來簡化解法。

示例 4

問題陳述

假設彈性體上一點的應力狀態為${\textstyle {\boldsymbol {\sigma }}}$，確定主應力和原始方向與最大剪應力方向之間的夾角。應力單位為 MPa。

${\boldsymbol {\sigma }}={\begin{pmatrix}18&12&9\\12&12&-6\\9&-6&6\end{pmatrix}}$

示例 5

問題陳述

用數學和文字解釋應用變換張量 ${\textstyle {\boldsymbol {T_{1}}}}$, ${\textstyle {\boldsymbol {T_{2}}}}$,${\textstyle {\boldsymbol {T_{3}}}}$, 和 ${\textstyle {\boldsymbol {T_{4}}}}$ 對向量 ${\textstyle {\boldsymbol {a}}}$ 的影響。將相同的變換應用於二階張量 ${\textstyle {\boldsymbol {Z}}}$。

${\boldsymbol {T_{1}}}={\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}}~{\boldsymbol {T_{2}}}={\begin{pmatrix}-1&0&0\\0&-1&0\\0&0&-1\end{pmatrix}}~{\boldsymbol {T_{3}}}={\begin{pmatrix}-1&0&0\\0&1&0\\0&0&-1\end{pmatrix}}~{\boldsymbol {T_{4}}}={\begin{pmatrix}cos\left(\theta \right)&0&sin\left(\theta \right)\\0&1&0\\-sin\left(\theta \right)&0&cos\left(\theta \right)\end{pmatrix}}$

${\boldsymbol {a}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}~{\boldsymbol {Z}}={\begin{pmatrix}Z_{11}&Z_{12}&Z_{13}\\Z_{21}&Z_{22}&Z_{23}\\Z_{31}&Z_{32}&Z_{33}\end{pmatrix}}$

解決方案

回顧張量乘法的定義和愛因斯坦求和約定，我們知道二階張量 ${\boldsymbol {T}}$ 作用於向量 ${\boldsymbol {a}}$ 將會不可避免地產生類似於以下形式的項

$a'_{2}=a_{1}T_{11}+a_{2}T_{12}+a_{3}T_{13}$

這與你之前見過的“普通”矩陣乘法類似。相比之下，將二階變換張量應用於二階張量 ${\boldsymbol {Z}}$ 需要進行雙重求和，這將產生類似於以下形式的項

$Z'_{12}=T_{11}T_{21}Z_{11}+T_{11}T_{22}Z_{12}+T_{11}T_{23}Z_{13}+T_{12}T_{21}Z_{21}+T_{12}T_{22}Z_{22}+T_{12}T_{23}Z_{23}+T_{13}T_{21}Z_{31}+T_{13}T_{22}Z_{32}+T_{13}T_{23}Z_{33}$

在處理這種包含 9 個項的求和時，通常建議使用軟體包來簡化工作。結果在此給出。

變換張量 1 的結果是

${\boldsymbol {a'}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}~{\boldsymbol {Z'}}={\begin{pmatrix}Z_{11}&Z_{12}&Z_{13}\\Z_{21}&Z_{22}&Z_{23}\\Z_{31}&Z_{32}&Z_{33}\end{pmatrix}}$

這對應於恆等變換，即不修改張量。

變換張量 2 的結果是

${\boldsymbol {a'}}={\begin{pmatrix}-a_{1}\\-a_{2}\\-a_{3}\end{pmatrix}}~{\boldsymbol {Z'}}={\begin{pmatrix}Z_{11}&Z_{12}&Z_{13}\\Z_{21}&Z_{22}&Z_{23}\\Z_{31}&Z_{32}&Z_{33}\end{pmatrix}}$

這種變換是反演變換。這可以在向量的行為中看到。有趣的是，它使 ${\boldsymbol {Z}}$ 不變。

變換張量 3 的結果是

${\boldsymbol {a'}}={\begin{pmatrix}-a_{1}\\a_{2}\\-a_{3}\end{pmatrix}}~{\boldsymbol {Z'}}={\begin{pmatrix}Z_{11}&-Z_{12}&Z_{13}\\-Z_{21}&Z_{22}&-Z_{23}\\Z_{31}&-Z_{32}&Z_{33}\end{pmatrix}}$

此變換涉及圍繞 $x_{1}$ 和 $x_{3}$ 方向進行映象。這等效於繞 $x_{2}$ 軸旋轉 $180$°。

變換張量 4 導致 $${\boldsymbol {a'}}={\begin{pmatrix}a_{1}cos\left(\theta \right)+a_{3}sin\left(\theta \right)\\a_{2}\\a3cos\left(\theta \right)-a_{1}sin\left(\theta \right)\end{pmatrix}}~{\boldsymbol {Z'}}={\begin{pmatrix}Z_{11}cos\left(\theta \right)^{2}+Z_{13}cos\left(\theta \right)sin\left(\theta \right)+Z_{31}cos\left(\theta \right)sin\left(\theta \right)+Z_{33}sin\left(\theta \right)^{2}&Z_{12}cos\left(\theta \right)+Z_{32}sin\left(\theta \right)&Z_{13}cos\left(\theta \right)^{2}-Z_{11}cos\left(\theta \right)sin\left(\theta \right)+Z_{33}cos\left(\theta \right)sin\left(\theta \right)-Z_{31}sin\left(\theta \right)^{2}\\Z_{21}cos\left(\theta \right)+Z_{23}sin\left(\theta \right)&Z_{22}&Z_{23}cos\left(\theta \right)-Z_{21}sin\left(\theta \right)\\Z_{31}cos\left(\theta \right)^{2}-Z_{11}cos\left(\theta \right)sin\left(\theta \right)+Z_{33}cos\left(\theta \right)sin\left(\theta \right)-Z_{13}sin\left(\theta \right)^{2}&Z_{32}cos\left(\theta \right)-Z_{12}sin\left(\theta \right)&Z_{33}cos\left(\theta \right)^{2}-Z_{13}cos\left(\theta \right)sin\left(\theta \right)-Z_{31}cos\left(\theta \right)sin\left(\theta \right)+Z_{11}sin\left(\theta \right)^{2}\end{pmatrix}}$$ 此變換涉及圍繞 $x_{2}$-軸旋轉。 將 $180$° 代入 $\theta$° 將產生與變換張量 3 相同的結果。

示例 6

問題陳述

考慮應力狀態 ${\textstyle {\boldsymbol {\sigma }}}$。 寫出一個將參考系旋轉到主方向的變換張量。 應力以 MPa 為單位給出。

${\boldsymbol {\sigma }}={\begin{pmatrix}72&21&0\\21&32&0\\0&0&0\end{pmatrix}}$

解決方案

我們從示例 1 中知道，解決方案是繞 $\theta =23.2$ 旋轉 $x_{3}$ 軸，我們知道旋轉變換矩陣的形式來自示例 5，因此解決方案是

${\boldsymbol {\sigma }}={\begin{pmatrix}cos\left(\theta \right)&sin\left(\theta \right)&0\\sin\left(\theta \right)&cos\left(\theta \right)&0\\0&0&0\end{pmatrix}}$

其中 $\theta =23.2$.

示例 7

問題陳述

給定位移張量 ${\textstyle {\boldsymbol {e}}}$，確定旋轉張量和應變張量。

${\boldsymbol {e}}={\begin{pmatrix}0.001&0.001&0.002\\-0.001&0.002&0.002\\0.001&0.003&0.002\end{pmatrix}}$

解決方案

我們可以將任何張量分解為完全對稱和完全反對稱張量，得到反對稱旋轉張量

${\boldsymbol {\omega }}={\begin{pmatrix}0&{\frac {e_{12}-e_{21}}{2}}&{\frac {e_{13}-e_{31}}{2}}\\{\frac {e_{21}-e_{12}}{2}}&0&{\frac {e_{23}-e_{32}}{2}}\\{\frac {e_{31}-e_{13}}{2}}&{\frac {e_{32}-e_{23}}{2}}&0\end{pmatrix}}={\begin{pmatrix}0&0.001&0.0005\\-0.001&0&-0.0005\\-0.0005&0.0005&0\end{pmatrix}}$

以及對稱應變張量

${\boldsymbol {\varepsilon }}={\begin{pmatrix}e_{11}&{\frac {e_{12}+e_{21}}{2}}&{\frac {e_{13}+e_{31}}{2}}\\{\frac {e_{21}+e_{12}}{2}}&e_{22}&{\frac {e_{23}+e_{32}}{2}}\\{\frac {e_{31}+e_{13}}{2}}&{\frac {e_{32}+e_{23}}{2}}&e_{33}\end{pmatrix}}={\begin{pmatrix}0.001&0&0.0015\\0&0&0.0025\\0.0015&0.0025&0\end{pmatrix}}$

最終導致 ${\boldsymbol {e}}={\boldsymbol {\omega }}+{\boldsymbol {\varepsilon }}$.

示例 8

問題陳述

線上性、均勻、各向同性彈性理論中，對於給定的應力狀態（單位為 MPa），確定給定泊松比為 0.40、剪下模量為 50 GPa 時的應變狀態。確定靜水壓力、偏應力、應變膨脹和應變偏量。

${\boldsymbol {\sigma }}={\begin{pmatrix}10&2&2\\2&5&-3\\2&-3&-5\end{pmatrix}}$

解決方案

我們已經知道應力，所以要得到解，需要確定應變，可以透過以下公式確定

$\varepsilon _{ij}={\frac {1+\nu }{E}}\sigma _{ij}-{\frac {\nu }{E}}\sigma _{kk}\delta _{ij}$

我們已經知道泊松比 $\nu$ 和剪下模量 $G$，但要使用此公式，我們需要彈性模量 $E$。可以透過以下公式求得

$G={\frac {E}{2\left(1-\nu \right)}}$

可以轉換為

$E=2G\left(1-\nu \right)$

代入後得到 $E=60$ GPa。得到的應變張量為

${\boldsymbol {\varepsilon }}={\begin{pmatrix}{\frac {1+\nu }{E}}\sigma _{11}-{\frac {\nu }{E}}\left(\sigma _{22}+\sigma _{33}\right)&{\frac {\sigma _{12}}{2G}}&{\frac {\sigma _{13}}{2G}}\\{\frac {\sigma _{21}}{2G}}&{\frac {1+\nu }{E}}\sigma _{22}-{\frac {\nu }{E}}\left(\sigma _{11}+\sigma _{33}\right)&{\frac {\sigma _{23}}{2G}}\\{\frac {\sigma _{31}}{2G}}&{\frac {\sigma _{32}}{2G}}&{\frac {1+\nu }{E}}\sigma _{33}-{\frac {\nu }{E}}\left(\sigma _{11}+\sigma _{22}\right)\end{pmatrix}}={\begin{pmatrix}0.1667&0.0467&0.0467\\0.0467&0.0500&-0.0700\\0.0467&-0.0700&-0.1833\end{pmatrix}}.$

靜水壓力為

$\sigma _{m}={\frac {\sigma _{kk}}{3}}={\frac {\sigma _{11}+\sigma _{22}+\sigma _{33}}{3}}={\frac {10+5-5}{3}}=3.33{\text{ GPa}}$

應變膨脹為

$\Delta =\left(1+\varepsilon _{11}\right)\left(1+\varepsilon _{22}\right)\left(1+\varepsilon _{33}\right)-1=\left(1+0.1667\right)\left(1+0.0500\right)\left(1+0.1833\right)-1=0.4496$

得到平均應變為

$\varepsilon _{m}={\frac {\Delta }{3}}={\frac {0.4496}{3}}=0.1499$

(注意，當應變較小時 $\Delta \approx \varepsilon _{11}+\varepsilon _{22}+\varepsilon _{33}=0.400$，這將導致 $\varepsilon _{m}\approx 0.1333$。不幸的是，在這個例子中，應變相對較大。) 然後透過從其各自的張量對角線中減去平均應力和應變來確定偏應力和應變。

${\boldsymbol {\sigma '}}={\begin{pmatrix}10-3.33&2&2\\2&5-3.33&-3\\2&-3&-5-3.33\end{pmatrix}}={\begin{pmatrix}6.67&2&2\\2&1.67&-3\\2&-3&-8.33\end{pmatrix}}$

以及

${\boldsymbol {\varepsilon '}}={\begin{pmatrix}0.1667-0.1499&0.0467&0.0467\\0.0467&0.0500-0.1499&-0.0700\\0.0467&-0.0700&-0.1833-0.1499\end{pmatrix}}={\begin{pmatrix}0.0168&0.0467&0.0467\\0.0467&0.0999&-0.0700\\0.0467&-0.0700&-0.3332\end{pmatrix}}$

例 9

問題陳述

線上性、均勻、各向同性彈性理論中，給定應變狀態，確定給定 100 GPa 的體積模量和 Lam${\acute {e}}$ 引數為 50 GPa 的應力狀態。找出靜水壓應力、偏應力、應變膨脹和應變偏量。

${\boldsymbol {\varepsilon }}={\begin{pmatrix}0.002&0.002&0.001\\0.002&0.002&0.001\\0.001&0.001&-0.001\end{pmatrix}}$

解決方案

我們已知應變，因此需要找出應力來得到解。應力可透過以下公式計算

$\sigma _{ij}={\frac {E}{1+\nu }}\varepsilon _{ij}-{\frac {\nu E}{\left(1+\nu \right)\left(1-2\nu \right)}}\varepsilon _{kk}\delta _{ij}$

其中 ${\frac {\nu E}{\left(1+\nu \right)\left(1-2\nu \right)}}$ 是拉梅引數 $\lambda$。由於

$G={\frac {E}{2\left(1+\nu \right)}}$

以及

$G={\frac {3\left(K-\lambda \right)}{2}}$

我們知道

${\frac {E}{\left(1+\nu \right)}}=3\left(K-\lambda \right)$

應力表示式變為

$\sigma _{ij}=3\left(K-\lambda \right)\varepsilon _{ij}+\lambda \varepsilon _{kk}\delta _{ij}$

代入求解得出

${\boldsymbol {\sigma }}={\begin{pmatrix}0.45&0.3&0.15\\0.3&0.45&0.15\\0.15&0.15&0.0\end{pmatrix}}$GPa

靜水壓力為

$\sigma _{m}={\frac {\sigma _{kk}}{3}}={\frac {\sigma _{11}+\sigma _{22}+\sigma _{33}}{3}}={\frac {0.45+0.45+0.0}{3}}=0.30{\text{ GPa}}$

應變膨脹為

$\Delta =\left(1+\varepsilon _{11}\right)\left(1+\varepsilon _{22}\right)\left(1+\varepsilon _{33}\right)-1=\left(1+0.002\right)\left(1+0.002\right)\left(1-0.001\right)-1=0.003$

得到平均應變為

$\varepsilon _{m}={\frac {\Delta }{3}}={\frac {0.003}{3}}=0.001$

一個有趣的觀察結果是，應變膨脹和靜水（平均）應力與體積模量有關 $\sigma _{m}=K\Delta$，在本例中為 $0.3=100\times 0.003$。在進行計算時，使用已知檢查點（如這些檢查點）來驗證您的工作非常重要。

然後透過從各自張量的對角線上減去平均應力和應變來確定偏應力和應變。

${\boldsymbol {\sigma '}}={\begin{pmatrix}0.45-0.30&0.30&0.15\\0.30&0.45-0.30&0.15\\0.15&0.15&0.00-0.30\end{pmatrix}}={\begin{pmatrix}0.15&0.30&0.15\\0.30&0.15&0.15\\0.15&0.15&-0.30\end{pmatrix}}$

以及

${\boldsymbol {\varepsilon '}}={\begin{pmatrix}0.002-0.001&0.002&0.001\\0.002&0.002-0.001&0.001\\0.001&0.001&-0.001-0.001\end{pmatrix}}={\begin{pmatrix}0.001&0.002&0.001\\0.002&0.001&0.001\\0.001&0.001&-0.002\end{pmatrix}}$

示例 10

問題陳述

對於一個立方氧化鋯單晶，其彈性常數約為 $c_{11}=575$，$c_{12}=115$ 和 $c_{44}=75$ GPa，確定在 $\left[100\right]$ 方向上施加 0.001 的單軸應變所需的彈效能量。確定在 $\left[110\right]$ 方向上施加 0.001 的單軸應變所需的彈效能量。計算齊納各向異性比。使用各向同性彈性理論，彈性模量為 200 GPa，泊松比為 0.3，計算施加 0.001 的單軸應變所需的彈效能量。

解決方案

假設 $\left[100\right]$ 在 $x_{1}$ 方向上。彈效能量，$U_{o}$，是

$U_{o}={\frac {1}{2}}\sigma _{ij}\varepsilon _{ij}$

所以

$dU_{o}={\frac {1}{2}}\sigma _{ij}d\varepsilon _{ij}$

在各向異性彈性理論的情況下

$\sigma _{ij}=c_{ijkl}\varepsilon _{kl}.$

在這種情況下，所有 $\varepsilon _{ij}=0$ 除 $\varepsilon _{11}=0.001$。因此，所有 $\sigma _{ij}=0$ 除 $\sigma _{11}=c_{1111}\varepsilon _{11}$，$\sigma _{22}=c_{1122}\varepsilon _{22}$，以及 $\sigma _{33}=c_{1122}\varepsilon _{33}$。

代入上述方程：

${\begin{aligned}dU_{0}&=\varepsilon _{11}c_{1111}d\varepsilon _{11}+\underbrace {\varepsilon _{11}c_{1122}\ d\varepsilon _{22}+\varepsilon _{11}c_{1122}\ d\varepsilon _{33}} _{=\ 0\ upon\ integration}\\&=\varepsilon _{11}c_{1111}d\varepsilon _{11}\\\\U_{0}&=\int _{0}^{\varepsilon _{11}\ =\ 0.001}\varepsilon _{11}c_{11}d\varepsilon _{11}\\&=\left.c_{11}{\varepsilon _{11}^{2} \over 2}\ \right|_{0}^{0.001}\\&=(575*10^{9}\ Pa){0.001^{2} \over 2}\\&=288\ kJ\end{aligned}}$

例 11

問題陳述

對於立方氧化鋯單晶，其彈性常數約為 $c_{11}=575$, $c_{12}=115$ 以及 $c_{44}=75$ GPa，確定在 $\left[100\right]$ 方向上施加 0.001 的單軸應變，然後在 $\left(001\right)$ 面上沿 $\left[010\right]$ 方向施加 0.001 的剪下應變所需的彈效能量。

解決方案

按照給定的操作順序，首先我們在 $[100]$ 方向上施加 $0.001$ 的單軸載荷。（也在示例 10 中涵蓋）

請注意，我們的通用方程式是 ${\textstyle dU=\sigma _{ij}\ d\varepsilon _{ij}}$，以及 ${\textstyle \sigma _{ij}=c_{ijkl}\varepsilon _{kl}}$。

重新說明應變張量：

$\varepsilon =\left({\begin{matrix}\varepsilon _{11}&0&0\\0&0&0\\0&0&0\end{matrix}}\right)$

由此我們得到非零應力張量：

$\sigma =\left({\begin{matrix}\varepsilon _{11}c_{11}&0&0\\0&\varepsilon _{11}c_{12}&0\\0&0&\varepsilon _{11}c_{12}\end{matrix}}\right)$

因此，唯一非零的 $d\varepsilon _{ij}$ 是 $d\varepsilon _{11}$，透過對我們 ${\textstyle dU}$ 公式的積分，我們得到：$U_{1}=288\ kJ$

現在，讓我們在 $(100)$ 面上施加 $0.001$ 的剪下力，在 $[010]$ 方向上。

我們的新應力張量是：

$\sigma =\left({\begin{matrix}\varepsilon _{11}c_{11}&\varepsilon _{12}c_{44}&0\\\varepsilon _{12}c_{44}&\varepsilon _{11}c_{12}&0\\0&0&\varepsilon _{11}c_{12}\end{matrix}}\right)$

這裡，唯一非零的項是 $d\varepsilon _{12}$ 和 $d\varepsilon _{21}$。由於對稱性，這兩個項是等效的，我們可以求解其中一個並將其答案乘以 2。

再次利用我們的基本能量方程，我們得到：

${\begin{aligned}dU&=\sigma _{ij}\ d\varepsilon _{ij}=\varepsilon _{12}c_{44}\ d\varepsilon _{12}\\\\U_{2}&=2\int _{0}^{\varepsilon _{12}}\varepsilon _{12}c_{44}\ d\varepsilon _{12}\\&=2\left[c_{44}{\varepsilon _{12}^{2} \over 2}\right]_{0}^{\varepsilon _{12}}\\&=(75*10^{9}\ Pa)0.001^{2}\\U_{2}&=75\ kJ\end{aligned}}$

最後，將 $U_{1}$ 和 $U_{2}$ 相加得到該組合變換的總能量，最終答案為 $363\ kJ$。

示例 12

問題陳述

對於立方氧化鋯的多晶體試樣，其彈性常數近似為 $c_{11}=575$，$c_{12}=115$，和 $c_{44}=75$ GPa，使用各向同性彈性理論以及 $200\ GPa$ 的彈性模量和 $0.3$ 的泊松比來計算施加應變狀態的彈效能量。

${\boldsymbol {\varepsilon }}={\begin{pmatrix}0.001&0.001&0.000\\0.001&0.000&0.000\\0.000&0.000&0.000\end{pmatrix}}$

如果多晶體材料的孔隙率約為 2%，這將使彈性模量發生多少變化？這將使施加應變的彈效能量發生多少變化？

解決方案

請注意，我們的通用方程式是 ${\textstyle dU=\sigma _{ij}\ d\varepsilon _{ij}}$，以及 ${\textstyle \sigma _{ij}=c_{ijkl}\varepsilon _{kl}}$。

這裡，我們可以用彈性模量和泊松比來表示應力：

$\sigma _{ij}={E \over 1+\nu }\varepsilon _{ij}+{\nu E \over (1+\nu )(1-2\nu )}\varepsilon _{kk}\partial _{ij}$

其中後一個常數等效於拉梅常數 ($\lambda$)：

$\lambda ={\nu E \over (1+\nu )(1-2\nu )}$

簡要解算拉梅常數，我們得到：

考慮到由於對稱性，$\varepsilon _{12}$ 等於 $\varepsilon _{21}$，該問題的非零應力為：

$\sigma =\left({\begin{matrix}{E \over 1+\nu }\varepsilon _{11}+\lambda \varepsilon _{11}&{E \over 1+\nu }\varepsilon _{12}&0\\{E \over 1+\nu }\varepsilon _{12}&\lambda \varepsilon _{11}&0\\0&0&\lambda \varepsilon _{11}\end{matrix}}\right)$

因此，我們可以寫出非零能量項為：

${\begin{aligned}dU&=\sigma _{ij}\ d\varepsilon _{ij}\\&=\left({E \over 1+\nu }+\lambda \right)\varepsilon _{11}\operatorname {d} \!\varepsilon _{11}+\left({E \over 1+\nu }+\lambda \right)\varepsilon _{12}\operatorname {d} \!\varepsilon _{12}+\left({E \over 1+\nu }+\lambda \right)\varepsilon _{21}\operatorname {d} \!\varepsilon _{21}+\lambda \varepsilon _{11}\operatorname {d} \varepsilon _{11}+\lambda \varepsilon _{11}\operatorname {d} \varepsilon _{11}\\&=\left({E \over 1+\nu }+\lambda \right)\varepsilon _{11}\operatorname {d} \!\varepsilon _{11}+2\left({E \over 1+\nu }+\lambda \right)\varepsilon _{12}\operatorname {d} \!\varepsilon _{12}\\\\U&=\left.\left({E \over 1+\nu }+\lambda \right){1 \over 2}\varepsilon _{11}^{2}\right|_{0}^{\varepsilon _{11}}+\left.\left({E \over 1+\nu }\right)\varepsilon _{12}^{2}\right|_{0}^{\varepsilon _{12}}\\&=288\ kJ\end{aligned}}$