物理習題/靜電學

電場疊加原理

1. 用文字和公式說明電場的疊加原理。

圖示疊加原理。

在物理學中，電場疊加原理假設，對於所有線性系統，由兩個或多個電荷在給定位置和時間引起的淨響應是每個電荷單獨引起響應的總和。

數學上可以寫成

${\vec {E}}={\vec {E}}_{1}+{\vec {E}}_{2}+{\vec {E}}_{3}+...+{\vec {E}}_{n}=\sum _{i=1}^{n}{\vec {E}}_{i}=\sum _{i=1}^{n}{\frac {1}{4\pi \epsilon _{0}r^{2}}}{\vec {u_{r}}}_{i}$

注意這是一個向量方程。因此必須使用向量規則新增分量。

求偶極子的電場

1. 電偶極子是匹配的，相等但相反的電荷，以固定距離隔開。求偶極子的電場。對三種情況進行求解

a. 求偶極子電荷軸之間垂直的電場。求遠場近似值。

b. 求偶極子電荷軸上的電場。將這種情況的遠場近似值與上面的 a) 進行比較。

c. 求包含偶極子電荷的平面中垂直的電場

水分子。水分子由於電子在“彎曲”結構中的不均勻共享而具有電偶極矩。電荷在中間（紅色陰影）有負電荷，在兩端（藍色陰影）有正電荷。

在物理學中，電偶極矩是衡量電荷系統中正負電荷分離的量度，即衡量電荷系統總極性的量度。它對於理解實際問題（如電容器的構造）非常重要。

求偶極子電荷軸之間垂直的電場

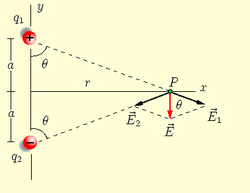圖 1：電偶極子

為了確定由圖 1 中以 2a 距離隔開的偶極子電荷產生的電場，我們只需將每個電荷單獨產生的電場相加。注意電場是向量。

${\vec {E}}={{\vec {E}}_{1}}+{{\vec {E}}_{2}}$

每個電荷（r）到測量電場點的距離是

$r={\sqrt {a^{2}+x^{2}}}$

第一個電荷（q₁）產生的電場（E₁）的大小和第二個電荷（q₂）產生的電場（E₂）的大小相同，儘管方向不同。

$E_{1}=E_{2}={\frac {1}{4\pi \epsilon _{0}}}{\frac {q}{r^{2}}}={\frac {1}{4\pi \epsilon _{0}}}{\frac {q}{a^{2}+x^{2}}}$

沿x軸方向的電場分量 $E_{1_{x}}$ 和 $E_{2_{x}}$ 大小相等，方向相反，相互抵消。

$E_{1_{x}}+E_{2_{x}}=0$

由於電場向量的水平分量相互抵消，因此將 ${{\vec {E}}_{1}}$ 和 ${{\vec {E}}_{2}}$ 求和，就簡化為將 $E_{1_{y}}$ 和 $E_{2_{y}}$ 求和。此外，垂直分量的幅度相同， $E_{1_{y}}=E_{2_{y}}$。由於 $\cos \theta ={\frac {adjacent}{hypotenuse}}$，求垂直分量就簡化為

$E_{1_{y}}=E_{2_{y}}=E_{1}\cos \theta \,\!$ 或者：$E_{y}=2E_{1}\cos \theta \,\!$

但我們也知道

$\cos \theta ={\frac {a}{\sqrt {a^{2}+x^{2}}}}$

因此，我們可以將此代入 $E\,\!$ 的方程，得到

$E=2E_{1}\cos \theta \,\!={\frac {2}{4\pi \epsilon _{o}}}{\frac {q}{a^{2}+x^{2}}}{\frac {a}{\sqrt {a^{2}+x^{2}}}}={\frac {1}{4\pi \epsilon _{o}}}{\frac {2aq}{(a^{2}+x^{2})^{\frac {3}{2}}}}$

在遠離偶極子的區域，x遠大於a (x>>a)。這通常被稱為“遠場”區域。我們可以透過提取x來找到場在遠場區域的行為。

$E={\frac {1}{4\pi \epsilon _{o}}}{\frac {2qa}{(a^{2}+x^{2})^{\frac {3}{2}}}}={\frac {1}{4\pi \epsilon _{o}}}{\frac {2qa}{x^{3}}}{\frac {1}{(1+{({\frac {a}{x}})}^{2})^{\frac {3}{2}}}}$

透過觀察，我們可以得出結論，當 x>>a 時，它將趨近於

$E\approx {\frac {1}{4\pi \epsilon _{o}}}{\frac {2qa}{x^{3}}}$

對於某些分析來說，一個重要的問題可能是：遠場近似在哪個範圍內有效？我們可以透過使用二項式展開來找出答案（如果您需要，可以在本節的下一部分中複習二項式展開）。

$E={\frac {1}{4\pi \epsilon _{o}}}{\frac {2qa}{(a^{2}+x^{2})^{\frac {3}{2}}}}={\frac {1}{4\pi \epsilon _{o}}}{\frac {2qa}{x^{3}}}{\frac {1}{(1+{({\frac {a}{x}})}^{2})^{\frac {3}{2}}}}$

我們將展開

${\frac {1}{(1+{({\frac {a}{x}})}^{2})^{\frac {3}{2}}}}$$=(1+{({\frac {a}{x}})}^{2})^{-{\frac {3}{2}}}=1-{\frac {3}{2}}{({\frac {a}{x}})}^{2}+...$

如果您只想在近似值引入的誤差小於 1% 時使用它，那麼——由於第一項是單位，您希望第二項小於單位的 1/100，或者

${\frac {1}{100}}>{\frac {3}{2}}{\left({\frac {a}{x}}\right)}^{2}$

${\frac {2}{300}}>{\left({\frac {a}{x}}\right)}^{2}$

${\sqrt {\frac {2}{300}}}>{\left({\frac {a}{x}}\right)}$

$x>{\sqrt {150}}\cdot a$

因此，如果 x 比 a 大 12.3 倍，則該近似值在 1% 內有效。

二項式展開復習

二項式展開復習

$\mathbf {(1+a)^{n}} =1+{\frac {n}{1!}}\cdot a+{\frac {n(n-1)}{2!}}\cdot a^{2}+{\frac {n(n-1)(n-2)}{3!}}\cdot a^{3}+...$

$\mathbf {(1+a)^{-{\frac {3}{2}}}} =1+{\frac {1}{1!}}\cdot {\frac {-3}{2}}\cdot a+{\frac {1}{2!}}\cdot {\frac {-3}{2}}\cdot {\frac {-5}{2}}\cdot a^{2}+{\frac {1}{3!}}\cdot {\frac {-3}{2}}\cdot {\frac {-5}{2}}\cdot {\frac {-7}{2}}\cdot a^{3}+...$

非正式來源連結

尋找偶極電荷形成的軸線上電場

圖 2 - 計算偶極電荷線上電場的佈局。

淨電場是偶極電荷對電場的貢獻之和。

${\vec {E}}={{\vec {E}}_{1}}+{{\vec {E}}_{2}}$

在解決任何問題時，首先應該做的事情是透過簡單觀察來考慮你所知道的事情。在本例中，電荷的大小和佈局告訴我們一些事情。由於它們相等，並且我們知道點電荷的電場隨 1/r² 衰減，因此我們知道最近的電荷將始終占主導地位。此外，我們還知道，在我們計算電場的軸線上，電場將沒有垂直分量。

$E_{1_{y}}=E_{2_{y}}=0$

因此，現在我們將計算每個電荷在 x 方向上的電場大小：$E_{1_{x}}$ 和 $E_{2_{x}}$.

$E_{1}={\frac {1}{4\pi \epsilon _{0}}}{\frac {q}{{(r-a)}^{2}}}\qquad \qquad E_{2}={\frac {1}{4\pi \epsilon _{0}}}{\frac {-q}{{(r+a)}^{2}}}$

將向量大小$E_{1_{x}}$ 和 $E_{2_{x}}$ 相加

$E=E_{1_{x}}+E_{1_{x}}\,\!$

將上述方程代入，得到

$E={\frac {1}{4\pi \epsilon _{0}}}{\frac {q}{{(r-a)}^{2}}}+{\frac {1}{4\pi \epsilon _{0}}}{\frac {-q}{{(r+a)}^{2}}}={\frac {1}{4\pi \epsilon _{0}}}\left[{\frac {q}{{(r-a)}^{2}}}-{\frac {q}{{(r+a)}^{2}}}\right]={\frac {1}{4\pi \epsilon _{0}}}\ 4aq\ {\frac {r}{{(r^{2}-a^{2})}^{2}}}$

2qa 的數量定義為偶極矩 (p)，因此我們可以代入

$p=2qa\,\!$

透過這種代入，我們現在得到

$E={\frac {1}{2\pi \epsilon _{0}}}{\frac {pr}{{(r^{2}-a^{2})}^{2}}}$

考慮遠場情況（即 $r\,\!$ >> $a\,\!$ 的情況）

然後可以看出 $r^{2}\,\!$ >> $a^{2}\,\!$ 並且 $r^{2}-a^{2}\,\!$ 接近 $r^{2}\,\!$，這使我們能夠簡化遠場中的方程。

$E={\frac {1}{2\pi \epsilon _{0}}}{\frac {p}{r^{3}}}$

請注意，可以使用二項式定理，就像上面的部分一樣，找出該遠場近似值（x>>a）的有效位置。

找到與平面上的任何地方的偶極子相關的電場

既然您已經解決了兩種特殊情況，並確定偶極子場在很遠距離處（稱為遠場）以 ${\frac {1}{r^{3}}}$ 的速度衰減，因此找到軸外場的行為很有啟發性。

考慮一個電偶極子在點 $P\,\!$ 的場，該點的座標為 $(x,y)\,\!$，如圖所示。請注意，我們可以將座標表示為笛卡爾座標或圓柱座標。

電偶極子在平面的場。

$r_{1}={\sqrt {{(y+a)}^{2}+x^{2}}}\quad \cos \alpha ={\frac {y+a}{\sqrt {{(y+a)}^{2}+x^{2}}}}\quad \sin \alpha ={\frac {x}{\sqrt {{(y+a)}^{2}+x^{2}}}}$

$r_{2}={\sqrt {{(y-a)}^{2}+x^{2}}}\quad \cos \beta ={\frac {y-a}{\sqrt {{(y-a)}^{2}+x^{2}}}}\quad \sin \beta ={\frac {x}{\sqrt {{(y-a)}^{2}+x^{2}}}}$

在笛卡爾座標系中，可以按如下方式找到平面上任意點處每個電荷產生的電場：

${E_{r}}_{1}={\frac {1}{4\pi \epsilon _{0}}}{\frac {+q}{{(y+a)}^{2}+x^{2}}}\quad {E_{r}}_{2}={\frac {1}{4\pi \epsilon _{0}}}{\frac {-q}{{(y-a)}^{2}+x^{2}}}$

我們可以應用疊加原理並新增每個電荷產生的場，記住它們是向量，因此垂直分量加到垂直分量，水平分量加到水平分量。

首先找到標記為 $E_{x}\,\!$ 的水平座標。

${{E_{r}}_{1}}_{x}={\frac {1}{4\pi \epsilon _{0}}}{\frac {+q}{{(y+a)}^{2}+x^{2}}}\sin \alpha ={\frac {1}{4\pi \epsilon _{0}}}{\frac {+q}{{(y+a)}^{2}+x^{2}}}{\frac {x}{\sqrt {{(y+a)}^{2}+x^{2}}}}={\frac {1}{4\pi \epsilon _{0}}}{\frac {+qx}{{\left[{(y+a)}^{2}+x^{2}\right]}^{\frac {3}{2}}}}$

${{E_{r}}_{2}}_{x}={\frac {1}{4\pi \epsilon _{0}}}{\frac {-q}{{(y-a)}^{2}+x^{2}}}\sin \beta ={\frac {1}{4\pi \epsilon _{0}}}{\frac {-q}{{(y-a)}^{2}+x^{2}}}{\frac {x}{\sqrt {{y-a)}^{2}+x^{2}}}}={\frac {1}{4\pi \epsilon _{0}}}{\frac {-qx}{{\left[{(y-a)}^{2}+x^{2}\right]}^{\frac {3}{2}}}}}$

接下來找到標記為 $E_{y}\,\!$ 的兩個電荷的垂直分量，我們得到

${{E_{r}}_{1}}_{y}={\frac {1}{4\pi \epsilon _{0}}}{\frac {+q}{{(y+a)}^{2}+x^{2}}}\cos \alpha ={\frac {1}{4\pi \epsilon _{0}}}{\frac {+q}{{(y+a)}^{2}+x^{2}}}{\frac {y+a}{\sqrt {{(y+a)}^{2}+x^{2}}}}={\frac {1}{4\pi \epsilon _{0}}}{\frac {+q(y+a)}{{\left[{(y+a)}^{2}+x^{2}\right]}^{\frac {3}{2}}}}$

${{E_{r}}_{2}}_{y}={\frac {1}{4\pi \epsilon _{0}}}{\frac {-q}{{(y-a)}^{2}+x^{2}}}\cos \beta ={\frac {1}{4\pi \epsilon _{0}}}{\frac {-q}{{(y-a)}^{2}+x^{2}}}{\frac {y-a}{\sqrt {{y-a)}^{2}+x^{2}}}}={\frac {1}{4\pi \epsilon _{0}}}{\frac {-q(y-a)}{{\left[{(y-a)}^{2}+x^{2}\right]}^{\frac {3}{2}}}}$

將水平分量相加得到

$E_{x}={\frac {1}{4\pi \epsilon _{0}}}q\left\lbrack {\frac {x}{{\left[{(y+a)}^{2}+x^{2}\right]}^{\frac {3}{2}}}}-{\frac {x}{{\left[{(y-a)}^{2}+x^{2}\right]}^{\frac {3}{2}}}}\right\rbrack$

對於大的 r（大的 x，大的 y 或者它們的組合），它變成

$E_{x}={\frac {qa}{2\pi \epsilon _{0}}}{\frac {1}{r^{3}}}$

將垂直分量相加得到

$E_{y}={\frac {1}{4\pi \epsilon _{0}}}q\left\lbrack {\frac {y+a}{{\left[{(y+a)}^{2}+x^{2}\right]}^{\frac {3}{2}}}}-{\frac {y-a}{{\left[{(y-a)}^{2}+x^{2}\right]}^{\frac {3}{2}}}}\right\rbrack$

求電四極子的電場

圖 3 - 一種形式的電四極子

在垂直軸上某一點測得的電場，是由於水平軸上任何單個電荷產生的（如圖 3 所示），

$E_{q}={\frac {q}{4\pi \epsilon _{o}r^{2}}}$

因此，中間的電荷貢獻

$E_{2q}={\frac {2q}{4\pi \epsilon _{o}r^{2}}}$

而左、右電荷貢獻的總電場大小為

$E_{-q}={\frac {-q}{4\pi \epsilon _{o}(r^{2}+d^{2})}}$

透過觀察，我們可以看到電場的水平分量相互抵消。只剩下垂直分量。因此，我們乘以

$sin\theta ={\frac {r}{\sqrt {r^{2}+d^{2}}}}$

為了得到單個負電荷的電場垂直分量

$E_{-q}={\frac {-q}{4\pi \epsilon _{o}(r^{2}+d^{2})}}{\frac {r}{\sqrt {r^{2}+d^{2}}}}$

對於兩個負電荷，我們得到

$E_{-2q}={\frac {-2q}{4\pi \epsilon _{o}(r^{2}+d^{2})}}{\frac {r}{\sqrt {r^{2}+d^{2}}}}$

現在我們可以加起來得到電場的總垂直分量。

$E=E_{2q}+E_{-2q}={\frac {2q}{4\pi \epsilon _{o}r^{2}}}+{\frac {-2q}{4\pi \epsilon _{o}(r^{2}+d^{2})}}{\frac {r}{\sqrt {r^{2}+d^{2}}}}$

簡化為

$E={\frac {q}{2\pi \epsilon _{o}}}\left[{\frac {1}{r^{2}}}-{\frac {r}{{(r^{2}+d^{2})}^{\frac {3}{2}}}}\right]$

從分母的最後一項中提取 r³，得到

$E={\frac {q}{2\pi \epsilon _{o}}}\left[{\frac {1}{r^{2}}}-{\frac {r}{{r^{3}(1+({\frac {d}{r}})^{2})}^{\frac {3}{2}}}}\right]$

簡化為

$E={\frac {q}{2\pi \epsilon _{o}r^{2}}}\left[1-{\frac {1}{{(1+({\frac {d}{r}})^{2})}^{\frac {3}{2}}}}\right]$

因此，我們現在有一個很好的方程式可以計算電場。工程師可能會認為這已經足夠了，因為他們可以在需要的時候計算出數值，但物理學家想了解這個方程式在“遠場” (r >> d) 的情況下是如何表現的。幸運的是，我們有一個工具——二項式展開式——可以幫助我們解答遠場的問題，如下所示

$\left[1-{\frac {1}{{(1+({\frac {d}{r}})^{2})}^{\frac {3}{2}}}}\right]=\left[1-{{\left(1+\left({\frac {d}{r}}\right)^{2}\right)}^{-{\frac {3}{2}}}}\right]=\left[1-\left(1-{\frac {3}{2}}\left({\frac {d}{r}}\right)^{2}\right)+...\right]={\frac {3}{2}}\left({\frac {d}{r}}\right)^{2}$

將該結果代回原方程式中

$E={\frac {q}{2\pi \epsilon _{o}r^{2}}}{\frac {3}{2}}\left({\frac {d}{r}}\right)^{2}$

簡化後，我們發現，在遠場 (r >> d) 中，四極子的電場隨 ${\frac {1}{r^{4}}}$ 衰減。

$E={\frac {3qd^{2}}{4\pi \epsilon _{o}r^{4}}}$

與線電荷相關的電場

1. 一個非常長的固體非導電圓柱體，半徑為R₀，長度為L（R₀ << L），具有均勻的體積電荷密度ρ_E（C/m³）。對於遠離兩端的點，且r << L，
   1. 求所有r的電場，r為距圓柱體軸線的距離。您可能需要分別針對r < R₀和r > R₀給出表示式。證明電場在r = R₀處是連續的，即電場的兩個表示式在r = R₀處一致。
   2. 描述一個位於圓柱體內的小自由電荷Q（符號相反，即Q ρ_E < 0）的運動。求電荷繞圓柱體軸線振盪的頻率$\nu$。（注意：$\nu$，頻率，單位為赫茲，而$\omega$，角頻率，單位為弧度/秒。）
   3. 讓我們改變一下問題，假設我們有一個圓柱形電荷殼（半徑為R₀，σ_E，使得總電荷保持不變）。r < R₀或r > R₀區域的電場表示式如何變化？電場仍然連續嗎？給出合理的論據解釋為什麼我們可能不期望電場是連續的。

求具有均勻線電荷密度λ庫侖/米的有限線的電場

具有均勻線電荷密度的無限長直線。

圖示了具有線性電荷密度$\lambda \,\!={\frac {dq}{dx}}$的有限長直線電荷。電荷從x = -a延伸到x = +b，它們是任意的（雖然不是無限的），在圖中沒有顯示。

與無限長直線的推導一樣，該直線電荷的一小段dx在點P處產生的電場大小是電荷$dq=\lambda dx\,\!$產生的結果。

有了這個電荷，我們可以計算dq對P點的場貢獻（dE）為

$dE={\frac {1}{4\pi {\epsilon }_{0}}}{\frac {dq}{r^{2}}}={\frac {1}{4\pi {\epsilon }_{0}}}{\frac {\lambda dx}{x^{2}+y^{2}}}$           (1)

我們不能再根據對稱性來論證電場在距無限長直線電荷等距的任何點都相同，因此我們可以詳細地解決這個問題，我們將使用二維來解決。一旦我們獲得了二維的解，圍繞直線電荷的簡單旋轉將使我們能夠確定第三維的場。

電場是一個向量，我們將用$d{\vec {E}}$來表示。我們將將其分解為二維笛卡爾座標系中的分量

$dE_{x}=-dE\sin \theta \,\!$      和      $dE_{y}=dE\cos \theta \,\!$

電場在$dE_{x}\,\!$ 處的符號表示點相對於x軸的$d{\vec {E}}_{x}$ 位置。

我們可以透過積分來求出水平方向上的總電場$E_{x}$ 和垂直方向上的總電場$E_{y}$，從而確定點P處的${\vec {E}}$。注意$\sin \theta$ 用於求水平方向上的電場分量，而$\cos \theta$ 用於求垂直方向上的電場分量。

$E_{x}=\int dE_{x}=-\int _{x=-a}^{x=+b}\sin \theta \,dE$

以及

$E_{y}=\int dE_{y}=\int _{x=-a}^{x=+b}\cos \theta \,dE$

或者用完整的向量形式

${\vec {E}}=\int _{L}\,d{\vec {E}}=\int _{L}{\frac {1}{4\pi \epsilon _{0}}}{\frac {dq}{r^{2}}}{\vec {u_{r}}}=\int _{L}{\frac {1}{4\pi \epsilon _{0}}}{\frac {\lambda dx}{r^{2}}}{\vec {u_{r}}}$

在這個例子中，從電荷到點P的距離r可以用直角座標x和y表示。

$r={\sqrt {x^{2}+y^{2}}}$.

這使我們能夠使用以下公式計算點 P 上由電荷 dx 在 r 處產生的電場的強度：$dE={\frac {1}{4\pi {\epsilon }_{0}}}={\frac {1}{4\pi {\epsilon }_{0}}}{\frac {\lambda dx}{x^{2}+y^{2}}}$

$\sin \theta ={\frac {opposite}{hypotenuse}}={\frac {x}{\sqrt {x^{2}+y^{2}}}}$          以及         $\cos \theta ={\frac {adjacent}{hypotenuse}}={\frac {y}{\sqrt {x^{2}+y^{2}}}}$

然而，我們必須記住，該強度對應於向量$d{\vec {E}}$，它隨著沿著線的移動而變化。因此，我們必須找到$d{\vec {E}}$在 x 方向或 y 方向上的分量。

為了找到 x 方向上的分量$dE_{x}=-dE\sin \theta \,\!$，為了找到 y 方向上的分量，應用$dE_{y}=dE\cos \theta \,\!$。

場在 x 方向上的分量$d{\vec {E}}_{x}$可以透過從線源的一端 -a 積分到另一端 a 來找到。如果線源在左右兩側長度相等，則 x 方向上的淨場將如以下所示抵消。

$E_{x}=\int dE_{x}=-\int _{x=-a}^{x=+b}\sin \theta \,dE=-\int _{x=-a}^{x=+b}{\frac {x}{\sqrt {x^{2}+y^{2}}}}\,dE$

$E_{x}=\int _{x=-a}^{x=+b}{\frac {x}{\sqrt {x^{2}+y^{2}}}},{\frac {1}{4\pi {\epsilon }_{0}}}{\frac {\lambda dx}{x^{2}+y^{2}}}$        (2)

$E={\frac {\lambda }{4\pi {\epsilon }_{0}}}\int _{x=-a}^{x=+b}{\frac {xdx}{\left[{x^{2}+y^{2}}\right]^{\frac {3}{2}}}}$           (3)

$E_{x}={\frac {\lambda }{4\pi {\epsilon }_{0}}}\left[-{\frac {1}{\left[a^{2}+y^{2}\right]^{\frac {1}{2}}}}+{\frac {1}{\left[b^{2}+y^{2}\right]^{\frac {1}{2}}}}\right]$        (4)

保持 1

類似地，場 $d{\vec {E}}_{y}$ 的 y 分量可以透過從直線源的一端 -a 積分到另一端 a 來找到。

$E_{y}=\int dE_{y}=\int _{x=-a}^{x=+b}\cos \theta \,dE=\int _{x=-a}^{x=+b}{\frac {y}{\sqrt {x^{2}+y^{2}}}}\,dE$

代入上式，得到

$E_{y}=\int _{x=-a}^{x=+b}{\frac {y}{\sqrt {x^{2}+y^{2}}}}\,{\frac {1}{4\pi {\epsilon }_{0}}}{\frac {\lambda dx}{x^{2}+y^{2}}}={\frac {\lambda y}{4\pi {\epsilon }_{0}}}\int _{x=-a}^{x=+b}{\frac {dx}{\left[x^{2}+y^{2}\right]^{\frac {3}{2}}}}$        (5)

$E_{y}={\frac {\lambda y}{4\pi {\epsilon }_{0}}}\int _{x=-a}^{x=+b}{\frac {dx}{\left[x^{2}+y^{2}\right]^{\frac {3}{2}}}}$        (6)

$E_{y}={\frac {\lambda }{4\pi {\epsilon }_{0}y}}\left[{\frac {x}{\left[x^{2}+y^{2}\right]^{\frac {1}{2}}}}\right]_{x=-a}^{x=+b}$        (7)

求單位長度電荷量為 λ 庫侖的無限長直線的電場

具有均勻線電荷密度的無限長直線。

圖中顯示了一條無限長的線狀電荷，其線性電荷密度為 $\lambda \,\!={\frac {dq}{dx}}$.

在點 P 處測量到的由這條線狀電荷的一小段 dx 產生的電場的強度，是電荷 $dq=\lambda dx\,\!$ 的結果。

有了這個電荷，我們可以計算dq對P點的場貢獻（dE）為

$dE={\frac {1}{4\pi {\epsilon }_{0}}}{\frac {dq}{r^{2}}}={\frac {1}{4\pi {\epsilon }_{0}}}{\frac {\lambda dx}{x^{2}+y^{2}}}$           (1)

由於我們可以透過對稱性來論證，電場在與無限長直線電荷等距的任何點上都是相同的，因此我們可以用二維來求解這個問題。一旦我們得到了二維的解，圍繞線狀電荷的簡單旋轉就可以提供三維的場。

電場是一個向量，我們將用$d{\vec {E}}$來表示。我們將將其分解為二維笛卡爾座標系中的分量

$dE_{x}=-dE\sin \theta \,\!$      和      $dE_{y}=dE\cos \theta \,\!$

電場在$dE_{x}\,\!$ 處的符號表示點相對於x軸的$d{\vec {E}}_{x}$ 位置。

我們可以透過積分來求出水平方向上的總電場$E_{x}$ 和垂直方向上的總電場$E_{y}$，從而確定點P處的${\vec {E}}$。注意$\sin \theta$ 用於求水平方向上的電場分量，而$\cos \theta$ 用於求垂直方向上的電場分量。

$E_{x}=\int dE_{x}=-\int _{x=-\infty }^{x=+\infty }\sin \theta \,dE$

以及

$E_{y}=\int dE_{y}=\int _{x=-\infty }^{x=+\infty }\cos \theta \,dE$

在這些表示式中，$E_{x}\,\!$ 必須積分到零，因為垂直點 P 左側的每個電荷元素都有一個在右側的對應元素，因此它們對水平方向的場貢獻相互抵消。所以 ${\vec {E}}$ 僅指向垂直方向。至於對 $E_{y}\,\!$ 的電場貢獻，帶電線的右半部分和左半部分將做出相同的貢獻，所以我們可以寫成

$E=E_{y}=2\int _{x=0}^{x=+\infty }\cos \theta \,dE$

將上面的式子 (1) 代入這個方程，我們得到

$E=2\int _{x=0}^{x=+\infty }\cos \theta \,{\frac {1}{4\pi {\epsilon }_{0}}}{\frac {\lambda dx}{x^{2}+y^{2}}}={\frac {\lambda }{2\pi {\epsilon }_{0}}}\int _{x=0}^{x=+\infty }\cos \theta \,{\frac {dx}{x^{2}+y^{2}}}$          (2)

根據定義，$\tan \theta ={\frac {x}{y}}$，我們可以寫成$x=y\tan \theta \,\!$。對該表示式求導，得到：$dx=y{\sec }^{2}\theta d\theta \,\!$。將此代入 (2)，得到

$E={\frac {\lambda }{2\pi {\epsilon }_{0}}}\int _{x=0}^{x=+\infty }\cos \theta \,{\frac {y{\sec }^{2}\theta d\theta }{x^{2}+y^{2}}}={\frac {\lambda }{2\pi {\epsilon }_{0}}}\int _{x=0}^{x=+\infty }{\frac {y}{x^{2}+y^{2}}}\cos \theta {\sec }^{2}\theta d\theta$      (3)

應用更多三角關係：$\cos \theta ={\frac {y}{r}}$，   $\sec \theta ={\frac {r}{y}}\quad$    以及    $\quad x^{2}+y^{2}=r^{2}\,\!$，    我們可以建立等價關係

${\frac {y}{x^{2}+y^{2}}}\cos \theta {\sec }^{2}\theta d\theta ={\frac {y}{r^{2}}}{\frac {y}{r}}{\frac {r^{2}}{y^{2}}}={\frac {y}{ry}}={\frac {\cos \theta }{y}}$

這可以代入公式 (3) 以得到一個簡化的積分

$E={\frac {\lambda }{2\pi {\epsilon }_{0}y}}\int _{x=0}^{x=+\infty }\cos \theta d\theta$

為了評估這一點，我們只需要觀察到 $x\rightarrow 0\,\!$，$\theta \rightarrow 0\,\!$，類似地 $x\rightarrow +\infty \,\!$，$\theta \rightarrow {\frac {\pi }{2}}\,\!$，以簡化我們的積分範圍為

$E={\frac {\lambda }{2\pi {\epsilon }_{0}y}}\int _{\theta =0}^{\theta ={\frac {\pi }{2}}}\cos \theta d\theta ={\frac {\lambda }{2\pi {\epsilon }_{0}y}}{\Bigg [}\sin {\frac {\pi }{2}}-\sin 0{\Bigg ]}={\frac {\lambda }{2\pi {\epsilon }_{0}y}}$

這得出一個最終的解

$E={\frac {\lambda }{2\pi {\epsilon }_{0}y}}$

這可以推廣到距離線電荷 r 的任何點

$E={\frac {\lambda }{2\pi {\epsilon }_{0}r}}$