物理教科書/光
光是電磁輻射,波長範圍在人眼可見範圍內,或者更廣義地說,是指從紅外到紫外範圍內的任何電磁輻射。光的三個基本維度(以及所有電磁輻射)是
- 強度(或亮度或振幅,人類感知為光的亮度),
- 頻率(或波長,人類感知為光的顏色),以及
- 偏振(或振動角度,在普通情況下,人類無法感知)
由於波粒二象性,光同時表現出波和粒子的性質。
解釋光本質的現代理論是波粒二象性,由阿爾伯特·愛因斯坦在20世紀早期基於他對光電效應和普朗克結果的研究而提出。愛因斯坦確定光子的能量與其頻率成正比。更一般地,該理論指出,任何事物都具有粒子性和波動性,可以透過不同的實驗來展現其中的一種或另一種性質。如果一個物體具有很大的質量,那麼它的粒子性更容易被辨別,因此直到路易·德布羅意在1924年進行的實驗,人們才意識到電子也表現出波粒二象性。愛因斯坦因其在光子波粒二象性方面的工作獲得了1921年的諾貝爾獎,德布羅意則因將這一理論擴充套件到其他粒子而在1929年獲得了諾貝爾獎。
人眼檢測到不同的波長,然後由人腦解釋為顏色,從最長波長(最低頻率)的紅色到最短波長(最高頻率)的紫色。中間頻率被視為橙色、黃色、綠色、藍色和傳統意義上的靛藍色。

電磁頻譜中人眼無法看到/檢測到的範圍以外的波長被稱為紫外線(UV),在短波長(高頻率)端,以及紅外線(IR),在長波長(低頻率)端。雖然人類無法看到IR,但我們確實可以透過皮膚上的感受器來感知近紅外(更短波長、更高頻率、更高能量)作為熱量。能夠檢測紅外線並將其轉換為光的相機被稱為夜視相機。
人類無法感知紫外線輻射,除了以非常延遲的方式,因為皮膚過度暴露於紫外線會導致曬傷或皮膚癌。一些動物,如蜜蜂,可以看到紫外線輻射,而另一些動物,如響尾蛇,可以使用頭上的熱感應器來感知紅外線。
在研究折射、鏡子和透鏡時,我們忽略了光的波動性。
光既表現為波,也表現為粒子射線。當觀察光對大型物體(如玻璃立方體、鏡子和透鏡)的影響時,光可以被觀察到像一束微小的粒子一樣,可以被反射、引導或減速。
介質減慢光速——割草機類比
鏡子反射光——會聚鏡、發散鏡
透鏡引導光——會聚透鏡、發散透鏡


折射是指由於速度變化而導致的波方向改變。當波從一個具有特定折射率的介質傳播到另一個具有不同折射率的介質時,就會發生這種情況。在介質邊界處,波會改變方向;它的波長會增加或減少,但頻率保持不變。例如,光線透過玻璃時會發生折射;對這一概念的理解導致了折射望遠鏡的發明。
在右側的圖中,波紋從左側傳播,並穿過一個以一定角度傾斜的更淺區域。波紋在更淺的水中傳播速度更慢,因此波長減小,波在邊界處彎曲。虛線表示邊界法線。虛線表示波紋的原始方向。這種現象解釋了為什麼海邊的波紋永遠不會以一個角度撞擊海岸線。無論波紋在深水中以何種方向傳播,它們在進入靠近海灘的淺水區時總是朝向法線方向折射。
一個例子就是往水盆裡看。空氣的折射率約為1.003,水的折射率約為1.33。如果你看一個直的物體,比如鉛筆,斜著放在水中,物體看起來會在水面上彎曲。這是因為來自物體的光線在從水中進入空氣時發生彎曲。這使得水看起來比實際的要淺。
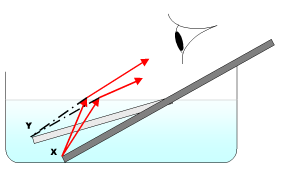
在圖中,深色矩形表示一根放在水盆中的鉛筆的實際位置。淺色矩形表示鉛筆的視覺位置。請注意,末端 (X) 看起來像在 (Y) 處,這個位置明顯比 (X) 淺。
折射也是彩虹形成的原因,也是白光透過玻璃稜鏡時分解成彩虹光譜的原因。玻璃的折射率高於空氣,不同頻率的光速不同(色散),導致它們以不同的角度折射。不同的頻率對應著觀察到的不同顏色。
光線在折射過程中彎曲的程度可以使用斯涅爾定律計算。
最近,一些具有負折射率的超材料被創造出來。
頻率是基礎
光速永遠不會改變。
光的頻率和波長 (λ) 會發生變化。

頻率是衡量重複事件在單位時間內發生次數的量。要計算頻率,需要固定一個時間間隔,計算該時間間隔內事件發生的次數,然後將該計數除以時間間隔的長度。
在 SI 單位中,結果以赫茲 (Hz) 為單位,以紀念德國物理學家海因裡希·魯道夫·赫茲。1 Hz 表示事件每秒重複一次。其他用於測量頻率的單位包括:每秒週期數、每分鐘轉數 (rpm)。
測量電磁波(如光)的頻率,以赫茲為單位,指的是每秒重複波形的迴圈次數。如果波是聲音,頻率決定了它的音調。
頻率與波長之間存在反比關係。頻率 f 等於波的速度 v 除以波長 λ(lambda)。
在電磁波在真空中傳播的特殊情況下,v = c,其中 c 是光在真空中的速度,這個表示式就變成了:
注意:記住f=f 當波從一種介質傳播到另一種介質時,它們的頻率基本保持不變,只有波長髮生變化。
要了解光如何穿過介質(如玻璃),可以使用一個人騎著自走式割草機的類比。
當這個人走在草地上時,他們會打滑並緩慢移動。當他們走到水泥地上時,他們不再打滑,速度加快了。割草機在草地上移動就像光在介質(如玻璃)中移動一樣,割草機在水泥地上移動就像光在真空中移動一樣。
此外,當割草機在水泥地上移動並以一定角度撞擊草地時,割草機的一個前輪會撞到草地並短暫減速,而另一個前輪會保持相同速度。這改變了割草機方向。就像一束光從真空中進入介質(如玻璃)時,當它撞擊介質時會改變方向。光線會朝垂直方向彎曲。
斯涅爾定律是一個簡單的公式,用於計算光在不同折射率的兩種介質之間傳播時的折射。它以其發現者荷蘭數學家威勒布羅德·斯涅爾(1580-1626)命名。

在右側的圖中,兩種折射率分別為 n1(左側)和 n2(右側)的介質在一個表面或介面(垂直線)處相遇。n2 > n1,光在第二種介質中的相速度較慢。
左側介質中的一束光線 PO 在點 O 處入射到介面。從點 O 開始,我們垂直於介面投影一條直線;這被稱為表面的法線(水平線)。法線與入射光線 PO 之間的角度被稱為入射角,θ1。
光線穿過介面進入右側的介質;這顯示為光線 OQ。它與法線所成的角度被稱為折射角,θ2。
斯涅爾定律給出了 θ1 和 θ2 之間的關係
注意,對於 θ1 = 0°(即垂直於介面的射線)的情況,解為 θ2 = 0°,無論 n1 和 n2 的值如何。換句話說,垂直於表面的入射射線永遠不會發生彎曲。
以上內容對於光從稠密介質到稀疏介質的傳播也適用;斯涅爾定律的對稱性表明,相同的射線路徑在相反方向上適用。
確定折射方向的一個定性規則是,稠密介質中的射線總是更靠近法線。記住這一點的一個簡便方法是,想象一下一輛汽車越過瀝青(稀疏介質)和泥土(稠密介質)之間的邊界。根據角度的不同,汽車的左輪或右輪會先越過新介質,導致汽車轉向。
當從稠密介質到稀疏介質移動時(即 n1 > n2),很容易驗證,當 θ1 超過一個稱為臨界角的值時,上述方程沒有解。
當 θ1 > θcrit 時,沒有折射光線出現,入射光線在介面處發生全內反射。
給定一個歸一化的射線向量 v 和一個歸一化的平面法向量 p,可以計算出歸一化的反射和折射射線:(注意實際角度 θ1 和 θ2 沒有計算出來)
這些餘弦值可以重複使用,並用於菲涅耳方程,計算所得光線的強度。在全內反射時,平方根會變成虛數,折射光線不再是真實的(顯然存在某種形式的折射光線,但它衰減非常快,呈指數級隨距離增加而衰減)。
斯涅爾定律可以從費馬原理推匯出來,費馬原理指出光線遵循最短時間路徑傳播。透過對光程長度求導,可以找到駐點,從而得到光線傳播的路徑。在費曼的經典類比中,低折射率區域被替換為沙灘,高折射率區域被替換為海洋,沙灘上的救援人員最快到達海里溺水者的方式是沿著遵循斯涅爾定律的路徑奔跑。








