地球/1e. 地球的運動和自轉

地球
1e. 地球的運動和自轉

地球每天的自轉

現在，當你閱讀這篇文章時，你的身體正以極快的速度穿越外太空。我們可以透過地球的周長來計算這種速度的一個分量，地球周長基於地球尺寸的橢圓模型，其赤道周長為 24,901.46 英里 (40,075.02 公里)。地球每天繞其軸旋轉一次，更準確地說，每 23 小時 56 分鐘 4 秒旋轉一次。如果你位於赤道，你的速度（速度加上方向）可以透過將 24,901.46 英里除以 23 小時 56 分鐘 4 秒來計算，等於每小時 1,040.45 英里。當然，這取決於你的緯度，隨著你接近兩極，速度會降低。

想象這種旋轉的一種方式是，如果你曾經看過一個老式的黑膠唱片旋轉，或者一個自由旋轉的腳踏車輪子。旋轉的唱片或輪子的中心軸是靜止的，而圓形的外緣在每次旋轉時都會以圓形的周長移動，你離旋轉中心越遠，你的速度就越快。換句話說，輪子越大，旋轉速度越快，單位時間內覆蓋的距離就越多。

早期的科學家，如伽利略，意識到了這種運動，並且很好奇為什麼我們在地球表面上感覺不到這種運動。如果你想象一隻螞蟻在一個旋轉的唱片上爬行，在邊緣，螞蟻會感覺到快速的運動，因為空氣呼嘯而過，並且感覺到一種離心力，試圖將可憐的螞蟻從旋轉的唱片上甩出去，但當螞蟻向中心爬行時，它的運動感會減弱。

如果你曾經玩過旋轉木馬，你也會感覺到同樣的情況，你離中心越近，你感覺到的旋轉運動就越少。然而，在地球上，我們感覺不到我們在赤道上以每小時 1,000 英里的速度行進，也感覺不到站在北極或南極附近是靜止的。

這種奇怪的悖論激發了艾薩克·牛頓研究運動，並在此過程中發現了萬有引力和牛頓運動定律，它支配著宇宙中所有物體的運動。他的發現發表在 1687 年的《自然哲學的數學原理》(自然哲學的數學原理) 中。

在我們討論為什麼我們感覺不到地球的自轉力之前，我們需要定義一些術語。

速度: 是物體在一定時間內運動的距離。例如，一輛汽車的速度可能為每小時 50 英里（每小時 80.5 公里）。
速度: 是速度加上空間方向。
加速度: 是速度變化率。例如，如果一輛汽車以每小時 50 英里的速度行駛 50 英里，並且沒有改變速度，那麼它的加速度為 0。一輛靜止不動且沒有移動的汽車也具有 0 加速度（在相應的參考系中）。這是因為在這兩個例子中，速度都沒有改變。

從數學上講，計算加速度更困難，一種方法是找到每個時間單位的速度變化。例如，一輛汽車在 5 小時的賽道上從 0 加速到每小時 50 英里，我們可以找到每 1 小時間隔的速度並對其進行平均。

在起跑線上，汽車的速度為每小時 0 英里。1 小時後，汽車的速度為每小時 10 英里。2 小時後，汽車的速度為每小時 20 英里。3 小時後，汽車的速度為每小時 30 英里。4 小時後，汽車的速度為每小時 40 英里。5 小時後，汽車的速度為每小時 50 英里。每小時，汽車的速度都會增加每小時 10 英里。

因此，平均加速度等於速度的平均變化量除以時間的平均變化量，在本例中，平均值為 10、10、10、10、10。平均加速度等於每小時 10 英里，每小時（或每小時平方）。

如果你懂一些微積分，我們可以找到所謂的瞬時加速度，或者使用以下公式找到加速度

\mathbf {a} =\lim _{{\Delta t}\to 0}{\frac {\Delta \mathbf {v} }{\Delta t}}={\frac {d\mathbf {v} }{dt}}

基本上，這個方程表明加速度是速度對時間的導數。

艾薩克·牛頓認為，我們在地球上感覺不到這種旋轉運動的原因是地球自轉的速度是恆定的。那些被設定為運動並且具有恆定速度的物體被稱為具有慣性。這些物體的加速度為零。

加速度是速度隨時間變化的情況。艾薩克·牛頓意識到，運動的物體將保持運動狀態，除非受到其他力的作用。這被稱為慣性定律。在外太空的失重環境中，宇航員可以旋轉籃球，它將繼續以該速度旋轉，除非它撞到另一個物體，或者另一個物體對該運動起作用。我們感覺不到地球自轉的原因是，所有物體都以這種恆定速度旋轉，或者表現出相同的慣性力。

然而，正如艾薩克·牛頓意識到的那樣，你應該感覺到由於這種旋轉力而產生的離心力。力是任何導致物體沿某個方向移動的相互作用。

牛頓提出了一個簡單的問題，為什麼像蘋果這樣的物體掉落到地球上，而不是由於地球的自轉而被甩到外太空呢？

他開始測量墜落物體的加速度。例如，從塔上掉下來的球。在球掉下來之前，它的速度是每秒 0 米，但在 1 秒後，球的速度是每秒 10 米。在 2 秒時，球的速度是每秒 20 米。在 3 秒時，球的速度是每秒 30 米。在 4 秒時，球的速度是每秒 40 米。在 5 秒時，球的速度是每秒 50 米。這聽起來很熟悉。每秒球的速度都會增加 10 米/秒。所以，墜落物體的加速度是每秒 10 米/秒（或平方秒）或 10 m/sec²。

一個世紀的實驗表明，地球表面上的墜落物體的加速度為 9.8 m/sec²。所有物體，無論它們的質量如何，都會以這種速度下降。

（實際上，物體在墜落時會撞擊空氣（氣體），運動中的物體將保持運動狀態，直到被另一個物體撞擊，在這種情況下是“空氣”粒子。這種空氣在自由落體過程中會增加阻力。因此，像降落傘這樣的物體，它們很寬，很寬，並且在墜落時會捕捉到大量的空氣，或者羽毛會下降得更慢。然而，9.8 m/sec² 的標準加速度仍然相同，但阻力會抵消這種力）。

墜落物體的力與質量和加速度都有關。

力由質量（以千克為單位測量）乘以加速度（以米每平方秒為單位測量）來衡量。艾薩克·牛頓因為以他命名的測量單位而獲得獎勵！

一個牛頓力的單位等於 1 千克 x 1 m/sec²。

因此，一個質量為 5 千克的保齡球將施加 5 千克 x 9.8 m/s² 或 49 牛頓的力。一個質量為 2 千克的海灘球將施加 2 千克 x 9.8 m/s² 或 19.6 牛頓的力。以牛頓為單位的物體是重量，因為重量包含質量和加速度。單位磅（磅）也是重量單位。

這種地球表面常見的加速度是重力加速度，為 9.8 m/sec²。艾薩克·牛頓意識到有一種力作用於物體使其保持在地球表面，並且該力與地球的質量直接相關。物體的質量越大，它的重力就越大。它也與物體的距離相關，物體越靠近，它受到的重力加速度就越大。利用這種數學關係，牛頓提出 9.8 m/sec² 的重力加速度可以用來計算地球的質量，使用此公式。

g={\frac {GMe}{re^{2}}}

g = 9.8 m/sec²，是地球表面的重力加速度。

re = 地球的半徑，或從地球中心到表面的距離，如果我們知道地球的周長就可以找到它。

Me = 地球的質量，以千克為單位測量。

G = 萬有引力常數，“有時稱為大 G”，是一個常數，單位為 m³/kg ⋅s²。

質量 = 密度 x 體積。密度是指物質的緊密程度，相對於另一種物質（如水）進行測量。換句話說，密度是指物質或物體漂浮或沉沒的程度。體積是指物體佔據的立方尺寸或空間。

艾薩克·牛頓並不知道大 G（萬有引力常數）的值，但他知道它是一個很小的數字，因為地球的質量和半徑非常大，而方程的結果必須等於 9.8 m/sec²。

尋找大 G 的探索

牛頓的工作促使新一代科學家試圖確定大 G，即萬有引力常數。確定大 G 的一種方法是確定地球的密度、體積和半徑。我們可以使用此公式求解大 G，

G={\frac {gr^{2}}{DV}}

其中 g 是地球上的重力加速度，r 是從地球中心到表面的地球半徑，D 是地球密度，V 是地球的體積。

艾薩克·牛頓的同事之一是埃德蒙·哈雷。哈雷是當時最傑出的科學家之一，他以計算彗星的週期性而聞名，事實上哈雷彗星以他的名字命名。然而，他不太以他關於地球是空心的的假設而聞名。他提出，地球的密度，因此是質量，比地球由非常緻密的固體核心組成要小得多。在 17 世紀後期和 18 世紀初，科學家們爭論地球的密度是多少。牛頓提出平均密度大約是水的 5 倍，而哈雷提出地球內部的平均密度小於水。問題是沒有人知道大 G 的值。

在接下來的一個世紀裡，關於地球密度（D 的值）的討論很多。探險隊前往世界各地的洞穴和黑暗洞穴，試圖找到通往傳說中地球空心中心的入口。這場爭論引起了一個小個子名叫約翰·米歇爾的人的興趣，他是英國約克郡一家教堂的主持人，但他閒暇時會涉足科學，並經常給當時的科學家（包括本傑明·富蘭克林）寫信。在他閒暇時，他想出一個實驗來測量大 G，方法是使用一組放在非常接近一組懸掛在連線到平衡杆的繩索上的較小但也非常緻密的鉛球的非常緻密的鉛球。當大鉛球放在小鉛球旁邊時，重力會使兩個球相互吸引。這種吸引力會導致平衡杆略微移動。為了測量這種移動或平衡杆角度的變化，一束光被反射到放在平衡杆頂部的鏡子。知道鉛球的質量和半徑，就可以求解萬有引力常數，即大 G，如果已知，就可以用來確定地球的密度。

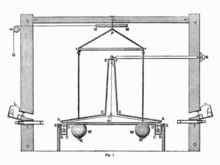
約翰·米歇爾的一位親密朋友是亨利·卡文迪許，一位出身名門望族的富裕科學家的兒子。亨利患有今天被稱為自閉症的疾病，因為他非常害羞，而且很難與除他親密朋友以外的人交談。後來，在 68 歲時，約翰·米歇爾去世，並將他的實驗留給了亨利·卡文迪許來完成。在一棟大樓裡，亨利重建了這個實驗，將鉛球放在他家附近，並計算出了大 G（萬有引力常數）的精確測量值，即 6.674×10−11 m³/kg⋅s²。

使用這個大 G 的數字，證明了地球不是空心的，實際上，它比地球表面附近的岩石密度更大，岩石密度約為 3 g/cm³，平均密度為 5.51 g/cm³，是水的 5.5 倍。這證明了地球內部不是空心的，而是比在地球表面發現的普通岩石密度要大得多。

亨利·卡文迪許精確計算了萬有引力常數，使你能夠計算任何物體的重力加速度，只需要知道它的質量和距其質量中心的半徑。物體質量、半徑和重力加速度之間的關係是理解地球運動的基本概念，不僅包括地球，還包括其他行星、衛星和恆星。以及相互作用的星體之間的引力。此外，它還解釋了為什麼宇宙中的大型物體在質量中心周圍呈現球形。重力加速度也解釋了為什麼我們感受不到地球的自轉，為什麼地球上的物體和物質不會被甩到外太空。它們被地球的引力吸引著。

地球會停止自轉嗎？

你是否擔心地球的自轉速度會減慢，或者將來有一天地球會停止自轉？

一天的長度是地球自轉一週的時間，在這期間，每個經度線都只面向太陽一次。如果地球的自轉速度隨著時間的推移而減慢，一天的長度就會增加，導致白天和黑夜變長。如今，地球完成一次自轉需要23小時56分鐘4.1秒。（注意，太陽精確地需要24小時才能到達每天天空中的最高點，這比地球的自轉時間略長，因為地球每天相對於太陽移動一點點。）

當然，白天和黑夜的時長會根據你的位置和時間而變化，因為地球繞著極軸自轉，而極軸相對於太陽傾斜了23.5°。這就是為什麼阿拉斯加（緯度較高）的人在7月份經歷的白天比赤道附近的人更長，而在12月份經歷的黑夜更長。需要問的問題是，地球的自轉速度是否一直保持在23小時56分鐘4.1秒？

就像一個旋轉的陀螺，地球的自轉速度可能正在減慢。測量地球每次自轉的時長需要每天用一個非常精確的秒錶點選，並記錄地球完成一次自轉所需的時間。在大多數情況下，它保持在23小時56分鐘4.1秒左右。然而，時長確實會有大約4到5毫秒的波動。換句話說，每天會增加或減少0.004到0.005秒。這些波動似乎以十年的週期出現，因此1860年代的白天比1920年代的白天短了0.006秒。這些十年的波動被認為是地球流體外核和周圍固體地幔之間角動量傳遞的結果，以及海洋潮汐摩擦力在自轉的地球表面來回移動時產生的摩擦力。每年都會出現較弱的波動，6月、7月和8月的白天比12月、1月和2月的白天短了0.001秒。這些較弱的波動是由於大氣和海洋摩擦力造成的，當地球自轉時，會產生一種叫做 “錢德勒擺動” 的振盪，以美國科學家S. C. 錢德勒命名。事實上，地球不僅僅是一個固體岩石，我們還有液態海洋和氣態大氣，它們會影響每一天的長度。就像你在一個裝滿溼衣服的洗衣機裡旋轉，根據衣服在每個旋轉週期的位置，旋轉本身的速度會有所不同。

氣候變化也會對一天的長度產生相當重要的影響。如果我們將最近一次冰川期（25000年前）的平均日長與今天進行比較，我們會發現當時的日長更短。這是因為地球的極地慣性矩減小了。當覆蓋極地大部分地區的巨大極地冰蓋開始融化時，地球的質量分佈從靠近旋轉星球中心的極地地區（作為冰蓋）轉移到赤道地區（作為融化的海水）。這種慣性矩的變化與你在溜冰者在旋轉過程中伸出手臂時觀察到的現象相同。旋轉速度會減慢。因此，隨著地球巨大的冰蓋在過去25000年中融化，地球就像旋轉的溜冰者一樣，將更多質量從中心向赤道外丟擲，導致自轉速度減慢。

雖然這些波動很有趣，但它們很小（幾毫秒），但我們想知道地球何時會停止自轉，為了這個問題，我們需要更長時間的日長記錄，追溯到數百萬年前。

化石生物記錄了地球過去數百萬年的每一年、每個月和每一天的長度。生活在海洋潮間帶的化石珊瑚會受到地球自轉和月球引力造成的兩次潮汐的影響，太陽的相對位置也會放大這種影響。這些水深變化會在生長環中留下記錄，以及迴圈沉積物，例如潮汐節律巖和條帶狀鐵建造。利用這些資訊，地球的自轉速度每百萬年增加了15.84秒。

艾薩克·牛頓提出，運動中的物體將保持運動狀態，除非受到其他力的作用。那麼是什麼力量減緩了地球的自轉速度呢？

答案是我們的近鄰——月球！

月球是地球唯一的天然衛星，赤道周長為10921公里（或6786英里），大約是地球的27%。它每27.32天繞地球執行一個朔望月，以一種叫做同步自轉的不尋常軌道執行。這導致了奇怪的事實：月球始終保持幾乎相同的一面或表面朝向地球。你從地球上在夜空中看不到的月球背面錯誤地被稱為月球的“黑暗面”。

兩側都每隔29.5個地球日被照亮一次，因為月球繞地球自轉，導致太陽照亮月球的不同階段。月球自轉軸相對於太陽的傾斜角度僅為5.14°，並且由於地球的自轉而減慢，最終與地球“潮汐鎖定”。

隨著月球繞地球執行的較慢的朔望月自轉，它就像一個緩慢的剎車作用於地球的自轉。地球會減速以匹配月球繞地球執行的27.32天或559.68小時的軌道。到那時，地球的自轉速度將與月球繞地球執行的軌道鎖定。

如果地球的自轉週期與現在的朔望月相同，那麼地球上的白天將持續27.32天，導致白天和黑夜的溫度極端，就像今天在月球表面一樣！這是你需要擔心的事情嗎？

不用擔心，地球的自轉速度被月球減慢了每百萬年僅僅幾秒，因此，直到1210億年後，地球才會與月球鎖定在這樣的死亡軌道上，到那時，地球和月球可能已經被膨脹的太陽吞噬了！

月球繞地球執行的影響可以透過觀察海洋潮汐的變化來觀察。當月球直接位於地球上的某個位置（地心）時，由於月球的引力作用，該位置的海洋會被拉向月球，從而在海岸線上產生高潮。在地球的另一側（即對蹠點）也會感受到同樣高的潮汐。當月球不在地球的地心或對蹠點時，就會觀察到低潮。由於液體水比構成固體地球的岩石更容易受到月球引力的影響，你可能對海洋潮汐更加熟悉，但也有地球潮汐，它會導致地球隨著月球的運動而膨脹。太陽也會對地球施加一些引力，並根據季節改變潮汐的大小。你現在可以解釋一天的長度，一個朔望月的長度，潮汐，但是什麼導致了一年的長度。

地球繞太陽執行，一年。

整個地球不僅在自轉，而且還在太空中沿著圍繞太陽執行的軌道執行。與月球不同，地球的極軸相對於太陽傾斜了23.5°，因此在這段繞太陽執行的旅程中，有一半時間北極朝向太陽，南極背向太陽。地球自轉傾斜23.5°導致北半球在更靠近太陽時（6月、7月、8月）白天更長，南半球白天更短，而北半球白天更短（11月、12月、1月）與南半球白天更長相對應。由於地球軸線的傾斜，我們有了春、夏、秋、冬四個季節，每個半球的季節都有所不同。

你可能會驚訝地發現，地球繞太陽執行的軌道不是一個完美的圓形，正如太陽系圖示中經常描繪的那樣，而是以橢圓軌道繞太陽執行。在地球上，可以透過記錄一年中每天中午太陽的位置來證明這一點，這將描繪出一個8字形，在天空中被稱為天體週年視運動圖。在8字形頂部的太陽中午位置將發生在夏至日，而8字形底部的太陽中午位置將發生在冬至日，天空中的兩個點之間的距離代表地球的傾斜角23.5°。然而，8字形的寬度是由於地球繞太陽執行的橢圓路徑造成的。8字形不是一個完美的8字形，而是其中一個環比另一個大。

這是由於太陽並不直接位於地球繞其執行的橢圓軌道的中心。在 12 月至 1 月期間，地球離太陽更近，而在 6 月至 7 月期間，地球離太陽更遠。地球最靠近太陽的年份被稱為近日點，而地球最遠離太陽的年份被稱為遠日點。

這與你想象的相反，因為在北半球，你在寒冷的冬季月份離太陽更近，而在炎熱的夏季月份，你離太陽更遠。

到太陽的距離從 0.9833 個天文單位到 1.0167 個天文單位不等，其中天文單位是天文單位，定義為地球到太陽的平均距離，即 1.5 億公里（9300 萬英里）。因此，地球到太陽的距離每年大約相差 500 萬公里（310 萬英里）。

雖然地球繞太陽執行的軌道似乎是一堆需要記憶的數字和事實，但發現太陽而不是地球是太陽系的中心是一個重大的科學發現。這種思維革命的原因是，幾個世紀以來，人們提出了一個同樣有效的解釋，來說明地球軌道的年度迴圈。

托勒密錯誤的太陽系地心模型

在法老克利奧帕特拉去世和埃及亞歷山大城被羅馬吞併後不久，一位名叫克勞狄烏斯·托勒密的天文學家住在亞歷山大城。托勒密的熱情是繪製星空，他注意到，每天晚上火星的執行路徑相對於夜空中其他恆星的執行路徑會有所不同。在公元 58 年左右的幾年時間裡，他記錄了火星在夜空中的執行路徑，證明了火星在幾個月的過程中在夜空中迴圈。例如，火星會在幾個星期內與恆星一起移動，但隨後會迴圈回來幾個星期，然後在繼續向它開始的方向移動之前，再次迴圈回來。

火星相對於背景恆星在幾個月內的明顯執行路徑，顯示了它相對於地球的軌道“逆行環”。

由於火星的執行路徑迴圈回來，托勒密認為這種運動是逆行運動，而當火星與恆星一起正常執行時，則是順行運動。托勒密遵循亞里士多德的希臘傳統，即地球是宇宙的中心。那麼為什麼火星和金星會在地球上迴圈呢？它們應該在夜空中沿著直線執行，因為它們繞地球執行，而不是繞太陽執行？他設計了一個複雜的太陽系地心模型，表明火星的軌道以及其他已知的行星（如金星）遵循本輪，即在它們繞地球執行的軌道之外的另一個圓形軌道。人們花了一千五百年才推翻托勒密的太陽系模型。

哥白尼正確的太陽系日心模型

尼古拉·哥白尼在 1543 年出版的《天體執行論》一書中發表了他的另一種觀點。太陽系日心說將太陽置於太陽系的中心，而不是地球。在這樣做的時候，哥白尼證明了本輪軌道實際上是由於從地球上觀察到火星在它自己繞太陽執行的軌道上執行而造成的。

由於地球離太陽比火星更近，因此看起來火星在夜空中的執行路徑有一個環，而實際上兩顆行星都在繞太陽執行，但地球的軌道比火星更靠近。

哥白尼認為，太陽系就像行星在圓形跑道上比賽一樣。地球在內圈，而火星在外圈。當地球沿著內圈的軌道執行時，對火星的外圈軌道的觀察會發生變化。逆行運動自然而然地作為從移動的地球視角觀察移動的火星的結果而產生。哥白尼拒絕了產生逆行運動所需的本輪，而行星繞太陽執行的軌道是圓形的。哥白尼的書是有史以來出版的最重要的科學書籍之一，但仍然需要一些修改，例如，地球繞太陽執行的軌道是橢圓形的，而不是圓形的，其他行星也是如此。

你在太空中以多快的速度飛行？

在本模組的開頭，我們討論了你在太空中以多快的速度飛行，並使用了地球的自轉或旋轉，現在我們可以新增地球繞太陽執行的軌道成分。地球繞太陽執行的距離是 9.4 億公里（5.84 億英里），它每 365.256 天完成一次。一年不能被天數平均分配，因此日曆必須每 4 年新增一天，或者說是“閏日”。我們可以確定這種繞太陽執行的運動速度，並確定地球及其表面的一切事物以每小時 66,619.94 英里或每小時 107,230.73 公里的驚人速度繞太陽執行。想象一下，當你坐在那裡閱讀本文時，你正以這種難以置信的速度坐在一顆圍繞恆星執行的行星上，速度是世界上最快飛機速度的 30 倍。因為你確實在這樣做！

這一驚人的事實，即你正乘坐一個快速移動的物體在太空中高速行駛，啟發了理查德·巴克敏斯特·富勒在 1969 年創造了地球只是一艘在浩瀚宇宙中航行的飛船的概念。地球號飛船，正如他稱我們的星球一樣，只是一艘巨大的船，就像一艘在空曠的宇宙海洋中航行的戰艦。他警告說，你和這艘“宇宙飛船”上的所有生命都應該為漫長的航行做好準備。

地球的銀河系之旅

約翰·米歇爾，來自英國約克郡的矮胖牧師，他設計了證明地球不是空心的實驗，他在 1784 年寫的一封信中提出，宇宙中可能存在一些物體，它們的質量如此之大，以至於它們的引力加速度甚至會吸收光線，他稱這些神秘的超大質量天體為“暗星”。如今，我們稱它們為黑洞。尋找宇宙中這些神秘超大質量天體的努力因他的建議而得到加強，即這些天體的引力效應可能在附近的可見天體中看到。然而，它們仍然是僅僅從牛頓方程式推匯出具有巨大質量（比太陽大數百萬倍）的天體的數學好奇現象。

1950 年，宇宙中還沒有人觀測到這些超大質量天體之一，而Jocelyn Bell，一個在英國寄宿學校的年輕女孩，正在為以烹飪和縫紉為主的女子課程而苦惱。當一個科學課程開設時，只有男孩被允許參加。她和她父母憤怒地抗議，最終她被允許和其他兩名女生一起參加科學課。Jocelyn Bell最喜歡物理學，1965 年她繼續在劍橋大學學習物理學。她加入了一個研究團隊，監聽來自外太空的無線電波。他們一直在接收來自微弱恆星的無線電波脈衝和雜音。科學家稱這些訊號為類星體無線電源，美國天文學家丘宏義簡稱為類星體。1967 年夏天，Jocelyn Bell 和她的教授安東尼·休伊什正在檢視新建造的射電望遠鏡陣列的列印輸出，這些陣列旨在探測來自太空的類星體訊號。她注意到每 1.3373 秒出現一個規律的脈衝模式，雖然很想將這些無線電波模式歸因於外星人，但他們開玩笑地稱這些規律的脈衝訊號為“小綠人”，但他們意識到，和其他科學家一樣，這個無線電訊號是由一個具有巨大引力的超大質量天體產生的。透過望遠鏡觀察，訊號來自一顆微弱的恆星，被認定為中子星，一顆極其巨大的恆星，以難以置信的速度旋轉，每 1.3373 秒發射一次電磁輻射脈衝。這些無線電訊號被認為是在星雲狀氣體被拉入這些超大質量恆星形成吸積盤時產生的，當這些氣體穿過吸積盤落入中子星時，會發出強大的磁場和無線電波——就像巨大的閃電。

科學家意識到，可以使用大型射電望遠鏡陣列來繪製這些來自太空的訊號到天空上，從而探測到這些超大質量天體。

研究人員將注意力集中在夜空中最亮恆星之一的中心，它實際上是一個名為M87的星團，也稱為室女座 A，是室女座中最亮的一點。它在 1781 年被梅西耶認定為一個星團，並被哈勃在 1931 年歸類為一個橢圓星雲。今天它被稱為一個包含數十億顆恆星的星系。

來自M87的無線電波表明，在其中心附近存在一個超大質量天體，代表一個黑洞。2019 年，事件視界望遠鏡，一個射電望遠鏡網路，將目光集中在這個點，並對來自其中心的訊號成像，產生了第一個黑洞影像，它看起來像一個幽靈般的黑暗斑點，周圍環繞著光。黑暗斑點的中心是一個質量是太陽 65 億倍、距離地球 5500 萬光年的天體。

事件視界望遠鏡還將目光集中在夜空中一個由無線電波於 1974 年首次探測到的點，該點被認為是我們自己的銀河系的中心，即銀河系。在夜空中，一串星星似乎在特別黑暗的夜晚掃過天空。這些恆星是你在你自己的星系中存在的最近的恆星鄰居。銀河系是一個包含數十億顆恆星的集合，包括圍繞一箇中心點旋轉的太陽。銀河系的中心位於靠近人馬座 A* （發音為“人馬座 A 星”）的恆星附近，位於人馬座。在這裡，已經觀察到附近的恆星圍繞一個點旋轉，該點是另一個黑洞的位置，該黑洞的質量是太陽的 400 萬倍，距離地球只有 25,000 光年。它是距離你最近的超大質量黑洞。

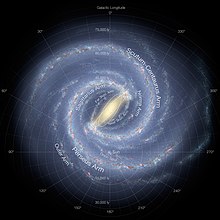
天文學家已經測量了太陽繞銀河系中心這個點的旋轉速度，並確定整個太陽系大約需要 2.4 億到 2.3 億年才能完成圍繞這個黑洞的銀河軌道執行。上一次我們太陽系佔據這個相對於人馬座 A*的空間，是在恐龍在地球上進化之前！

然而，不要認為太陽系圍繞這個點的執行速度很慢。地球和整個太陽系正以令人難以置信的速度沿著這條路徑前進。

鑑於 1 光年等於 5.879 x 1012 英里，並且繞行 1.5708 億光年的周長，或者說在 2.1024 x 1012 小時內繞行 9.23471 x 1017 英里的路徑需要 2.4 億年，我們的太陽系正在以每小時 439,246 英里的速度圍繞這個黑洞高速執行！

你確實身處一艘非常快的宇宙飛船，地球相對於其極軸的運動速度在每小時 0 到 1,040.45 英里（每小時 1674.44 公里）之間，具體取決於你的緯度。地球相對於太陽的運動速度為每小時 66,620 英里（每小時 107,214.5 公里），地球相對於人馬座 A*的銀河系運動速度為每小時 439,246 英里（每小時 706,898 公里）。

圖書頁面導航
上一頁	當前頁	下一頁
d. 如何使用指南針、六分儀和計時器在全球範圍內導航。	e. 地球的運動和自轉。	f. 時間的本質：太陽曆、陰曆和恆星曆。