等離子體聚變前言

本書旨在描述一些關於聚變能及其產生的基本考慮因素。然而，其重點不僅僅在於聚變能本身，還在於理解相關的物理現象，例如壓力。

自然界中的等離子體

薩哈方程指出

${\frac {n_{i}}{n_{n}}}=2.4*10^{21}{\frac {T^{3/2}}{n_{i}}}\exp -({\frac {U_{i}}{kT}})$,

其中 n_i 是離子密度，n_n 是中性原子密度，U_i 是氣體的電離能。

對於普通空氣而言

$n_{n}=3*10^{25}m^{-3}$

$T=300K$

$U_{i}=14,5eV(nitrogen)$

得出

${\frac {n_{i}}{n_{n}}}=10^{-122}$

這是一個極低的數值

當 U_i 僅為 kT 的幾倍時，電離率才會保持較低水平。

因此，在地球上不存在自然等離子體，只存在於溫度高達數百萬度的天體中。

數值示例

根據下面的公式（如果正確的話），太陽內部的壓力似乎在250萬個大氣壓的量級，而其（表面）溫度約為50000K。我們可以使用公式 p=nkT 計算粒子密度 (n)，使用這個公式，我計算出的 n 為 3,6E29（比空氣密度高約10000倍）。在這裡，我們可以使用薩哈方程計算氫離子 (n_i) 與中性氫原子 (n_n) 的比例 (n_i/n_n)，同時使用氫的電離能 (Ui=13,6eV)，得出比例為5,6%。

關於太陽壓力的未經證實的觀點

來自某全方向物體的光強 (I) 為

$I={\frac {P}{4\pi R^{2}}}$

其中 P 是輻射功率，R 是距離，這可能會導致

$\rho =\rho _{0}(1-{\frac {4\pi R^{2}}{4\pi b^{2}}})=\rho _{0}(1-{\frac {R^{2}}{b^{2}}})$

然後質量 (m) 為

$M=\int \rho dv=\int _{0}^{b}\rho 4\pi R^{2}dR$

其中 b 是太陽的半徑，R 是太陽中某個半徑，這給出

$M=4\pi \rho _{0}[{\frac {R^{3}}{3}}-{\frac {R^{5}}{5b^{2}}}]=4\pi \rho _{0}R^{3}[{\frac {1}{3}}-{\frac {R^{2}}{5b^{2}}}]$

然後壓力為

$p=\rho gh=\rho gR=\rho {\frac {GM}{R^{2}}}R=\rho {\frac {GM}{R}}$

因此

$p=\rho _{0}(1-{\frac {R^{2}}{b^{2}}})G4\pi \rho _{0}R^{2}({\frac {1}{3}}-{\frac {R^{2}}{5b^{2}}})$

平均密度為

${\tilde {\rho }}={\frac {M}{V}}$

和

$\rho =\rho _{0}(1-{\frac {R^{2}}{b^{2}}})$

因此

${\tilde {\rho }}={\frac {1}{b}}\int _{0}^{b}\rho _{0}(1-{\frac {R^{2}}{b^{2}}})dR$

這給出

${\tilde {\rho }}=2/3\rho _{0}$

結果是

$\rho _{0}={\frac {3}{2}}{\tilde {\rho }}={\frac {3M}{2V}}$

然後壓力為

$p=({\frac {3M}{2V}})^{2}(1-{\frac {R^{2}}{b^{2}}})G4\pi \rho _{0}R^{2}({\frac {1}{3}}-{\frac {R^{2}}{5b^{2}}})$

現在我們需要檢查 R 應該取什麼值，我在下面計算得出該函式有一個極小值/極大值（取決於你所處的方向），這個點可以透過常規求導並令導數為零來找到，對 R 求導該公式得到：

${\frac {2}{3}}-{\frac {32}{15}}({\frac {R}{b}})^{2}+{\frac {6}{5}}({\frac {R}{b}})^{4}=0$

我們透過代入進行變數替換：

$x=({\frac {R}{b}})^{2}$

這給出

$x^{2}-{\frac {160}{90}}x+{\frac {10}{18}}=0$

求解這個二階方程得到：

$x={\frac {16}{18}}-{\sqrt {({\frac {16}{18}})^{2}-{\frac {10}{18}}}}$

其中，只有根式前為減號的解是可能的，因為否則 R>b，數值解為：

$x=0,89-0,48=0,40$

因此

${\frac {R}{b}}=0,63\approx {\frac {2}{\pi }}$

我認出了這個值是全波整流訊號的直流值，那麼 b(太陽) 為 700Mm，這表明在 446Mm 半徑處存在一個極大值/極小值，物理手冊中指出：

$M(Sun)=333000m(Earth)$

和

$V(Sun)={\frac {4\pi b_{s}^{3}}{3}}=1,4\cdot 10^{27}$

不幸的是，物理手冊中沒有給出地球的質量，但我天真地嘗試透過將地球視為主要由水組成來估計它，b(地球)=6370km，我得到：

$m(Earth)\approx \rho _{H_{2}O}\cdot {\frac {4\pi b_{j}^{3}}{3}}=10^{24}$

由於這個估計，我得到：

$M=3,3\cdot 10^{29}$

這使得太陽的平均密度為：

${\tilde {\rho }}={\frac {M}{V}}=238kg/m^{3}$

我認為這相當低，但我們應該記住它是一種氣體/等離子體，而空氣的密度要低 200 多倍，重力常數則為

$G=6,62\cdot 10^{-}{11}$

有了這個值，我們現在可以計算太陽的壓力，結果是

$p=7\cdot 10^{9}Pa=70000atm=70ton/cm^{2}$

這是一個相當大的壓力，請記住，正常的空氣壓力就像用 1 公斤的力在一個桌子上戳一下手指，可以透過使用斯特藩-玻耳茲曼輻射定律來估算太陽的溫度，該定律指出強度與 T^4 成正比，這得出

${\frac {T_{s}^{4}}{4\pi (AU)^{2}}}={\frac {T_{j}^{4}}{4\pi R_{j}^{2}}}$

其中 AU 是天文單位，即太陽到地球的距離，Rj 是地球的半徑，使用這個公式，我們得到

$T_{s}=({\frac {AU}{R_{j}}})^{\frac {1}{2}}T_{j}$

其中 Tj=300K，Rj=6370km 以及 AU=1,5E11 得出

$T_{s}=46000K\approx 50000K$

現在我們有了太陽的壓力和溫度，就可以計算出粒子的密度，如下

$p=nkT$

這得出粒子的離子密度 (n_i) 為

$n_{i}=10^{28}$

這應該與普通空氣中的粒子密度進行比較，普通空氣的粒子密度約為 E25，因此太陽中的粒子密度似乎高出 1000 倍，然而我的計算結果表明，密度在向中心方向增加 50%，我順便說一下，使用了表面溫度，而表面溫度很可能在太陽的核心更高，如果我的公式是正確的，很明顯太陽核心的壓力可能比上述結果高出 7 倍（只需將 R=0 代入），使用上述薩哈方程和氫的電離能 13,6eV，我們現在可以計算出太陽中的離子比例為 11%。

我現在已經透過在維基百科中查詢資訊來修正了我對地球質量的估計，看來地球的質量高出 6 倍，這實際上使我的壓力估計高出 36 倍，因此太陽中的壓力應該是 2 500 000atm=2 500 000kg/cm^2！

基本考慮

當帶電粒子在磁場中運動時，以下方程適用

$m{\frac {dv}{dt}}=qvXB$

解決該方程的一個簡單方法是設定

$v=v_{0}e^{jwt}$

然後該方程變為

$mjwv_{0}e^{jwt}=qvXB=mjwv$

僅考慮大小，我們得到

$w_{c}={\frac {|q|B}{m}}$

而當 v=wr 時，我們得到

$r_{L}={\frac {mv}{|q|B}}$

其中 w_c 稱為迴旋頻率，r_L 稱為拉莫半徑。

這意味著粒子將以迴旋頻率和拉莫半徑繞力線旋轉。

這是等離子體能夠被磁場約束的最基本原因。

數值示例

如果我們看一下電子和大約 5T 的磁通密度（我認為 ITER 使用的磁通密度，但資訊不幸地在維基百科時代被刪除了），我們得到的迴旋頻率為 8E11 rad/s。我還記得 ITER 的熱能約為 10keV，使用下面的能量公式可以算出電子的速度約為 5,6E7 m/s，得到的拉莫半徑約為 70um。如果我們看一下質子（以相反的方向旋轉），迴旋頻率變為 4,8E8 rad/s，在相同的溫度下得到的速度為 1,4E6 m/s，得到的拉莫半徑為 2,9mm。也就是說，拉莫半徑大約分別為 0,1mm 和 1mm。

等離子體的能量和溫度

平均能量可以寫成

$E_{AV}={\frac {1}{2}}mv^{2}\approx kT$

對於每一個自由度，都有一個額外的 kT/2 （無論它意味著什麼），速度為

$v={\sqrt {\frac {2kT}{m}}}$

上面的能量方程符合麥克斯韋速度分佈函式

$f(v)=A\exp {(-{\frac {mv^{2}/2}{kT}})}$

其中常數 A 可以透過以下公式計算

$1=\int _{-\infty }^{\infty }f(v)dv$

這使我們得到

$A={\sqrt {\frac {m}{2\pi kT}}}$

這意味著

$<kT>={\frac {mv^{2}}{2}}$

其中 <kT> 是平均值，換句話說，有些粒子的“溫度”高於平均動能。

數值示例

分佈函式的指數部分在速度為 0 m/s 時最大，但曲線下的面積代表所有速度都被考慮在內的機率 1，這意味著必須將分佈函式對所有速度進行積分，從而透過將積分設定為 1 來確定常數 A。300K 時電子上的 A 為 6,2E-6。

eV 和一些常數

根據弗朗西斯·F·陳的說法，物理學家使用 eV 來避免混淆，但 kT 是用焦耳表示的，因此需要使用以下公式進行轉換：

$kT/q=eV$

電位是用伏特表示的，但它們的能量 (qU) 可以像原樣一樣被認為是用 eV 表示的。

讓我們列出一些常數

$k=1,38\cdot 10^{-23}J/K$

$q=1,6\cdot 10^{-19}As$

$m_{p}=1,67.2623\cdot 10^{-27}kg$

$m_{n}=1,67.4929\cdot 10^{-27}kg$

$m_{e}=9,10.9390\cdot 10^{-31}kg$

$h=6,63\cdot 10^{-34}Js$

$\mu _{0}=4\pi \cdot 10^{-7}Vs/Am$

$\epsilon _{0}=8,85\cdot 10^{-12}As/Vm$

推匯出電流環的磁通密度

電流環產生的磁場

從麥克斯韋方程組中我們可以得到

$\nabla \cdot B=0$

它可以被重寫為

$B=\nabla XA$

其中A可以是一個任意向量。

使用向量磁勢

$A={\frac {\mu _{0}}{4\pi }}\int _{v}{{\frac {J}{R}}dv}$

並意識到

$Jdv=JSdl=Idl$

我們根據畢奧-薩伐爾定律得到

$B={\frac {\mu _{0}I}{4\pi }}\oint _{c}{\frac {dlXa_{R}}{R^{2}}}$

定義

$dl=bd\phi a_{\phi }$

和

$R=a_{z}z-a_{r}b$

和

$dlXR=a_{\phi }bd\phi X(a_{z}z-a_{r}b)=a_{r}bzd\phi +a_{z}b^{2}d\phi$

並意識到r部分相互抵消，我們得到

$B={\frac {\mu _{0}I}{4\pi }}\int _{0}^{2\pi }a_{z}{\frac {b^{2}d\phi }{(z^{2}+b^{2})^{3/2}}}$

或者

$B={\frac {\mu _{0}I}{2}}{\frac {b^{2}}{(z^{2}+b^{2})^{3/2}}}={\frac {\mu _{0}I}{2}}{\frac {b^{2}}{R^{3}}}{\hat {z}}$

其中B的維度很明顯是

$B\propto {\frac {1}{R}}$

數值示例

如果 b=2m 且 I=100A，距離 (R) 為 1m 處的磁通密度 (B) 僅為 0,25mT，與某些 5T 的主要力線相比，這並不多，因此可以說，迴旋電流不影響 B 場。

推導帶電環路的電場強度

帶電環路的 E 場

可以這樣寫 E 場

$E={\frac {\rho _{L}}{4\pi \epsilon _{0}}}\int {\frac {dl'}{R^{2}}}={\frac {\rho _{L}}{4\pi \epsilon _{0}}}\int {\frac {dl'R}{R^{3}}}$

其中分母中的 R 是一個向量，像

$R=-b{\hat {r}}+z{\hat {z}}$

和

$dl'=bd\phi$

由於對稱性，不存在 r 分量，這給了我們

$R=z{\hat {z}}$

它可以被重寫為

$E={\frac {\rho _{L}}{4\pi \epsilon _{0}}}\int {\frac {bd\phi }{z^{2}}}{\hat {z}}$

或者

$E={\frac {\rho _{L}}{4\pi \epsilon _{0}}}\int {\frac {bd\phi }{R^{2}}}{\hat {z}}$

最後

$E={\frac {\rho _{L}}{4\pi \epsilon _{0}R^{2}}}2\pi b{\hat {z}}$

實際上它表示 Q/R^2，它與 E 有相同的“維度”，然後你可以觀察到對於正電荷，E 位於 z 方向，rho_L 可以被看作（並且不一定是均勻的）

$\rho _{L}={\frac {\sum q}{2\pi b}}$

或者

$\rho _{L}={\frac {\sum q}{2\pi r_{L}}}$

其中 E 的維度很明顯是

$E\propto {\frac {1}{R^{2}}}$

數值示例

如果質子的拉莫半徑 (b) 為 2.9 毫米，則其圓周可以容納 1.4E22 個質子，總電荷量為 0.22 微庫侖，這反過來又產生 12.7 微庫侖/米的線電荷密度 (rho_L)。在距離 (R) 為 1 米處，我們得到 2.2 千伏/米的電場強度 (E)，這並不算低（空氣的介電強度約為 5 兆伏/米），但這種情況永遠不會發生，因為粒子會不斷相互碰撞。

關於電流/帶電環路的未經證實的觀點

我手動恢復了關於電流環路產生的磁通密度 (B) 的章節，因為我認為它比我想象的要深刻得多。當然，電流在環路中旋轉，我們從中得到了一個 Bz 場，但是電流是運動中的電荷。我推測例如質子具有相同的拉莫半徑，這意味著質子沒有必要彼此並排圍繞力線旋轉，它們也可以像一串珍珠一樣互相追隨旋轉，本質上可以將其視為被質子塞滿的“珍珠項鍊”，質子的運動產生電流，進而產生 B 場。

我的想法是，質量和電荷相同的粒子以相同的迴旋頻率和拉莫半徑沿著力線旋轉。如果我們可以認為相同電荷的粒子實際上是“互相追隨”旋轉的，我們有兩種情況。

1) 由旋轉粒子圍繞區域性 Bz 場產生的電流（即來自電流的 B_phi，該電流的方向為 z 方向）會產生一個 B_phi 場，就我理解而言，如果電荷為正（並且在區域性 phi 方向運動），這會放大現有的 B_phi 場。

2) 當我們有一串粒子圍繞旋轉時，我們也會有一個靜態 E 場的“快照”。E 場似乎也會放大區域性 phi 方向的現有 E 場。

帶正電的粒子顯然具有正的 Ez 分量，我不確定，但根據洛倫茲力方程

$q(vXB)=m{\frac {dv}{dt}}$

並使用

$v_{r}=v_{0r}e^{jwt}$

和

$v_{\phi }=v_{0\phi }e^{jwt}$

併為了簡單起見認識到

$v=(0;v_{\phi };0)$

和

$B=(0;0;B_{z})$

運動必須是

$qv_{0\phi }e^{jwt}B_{z}=jwmv_{0r}e^{jwt}$

其中

$e^{jwt}$

可以簡化，我們剩下

$qv_{0\phi }B_{z}=jwmv_{0r}$

其中 0 僅表示幅度。去掉零，我們得到

$qv_{\phi }B_{z}=jwmv_{r}$

有了這些（新的）方向，實際上意味著迴旋頻率公式

$w_{c}={\frac {qB}{m}}$

是錯誤的，應該是

$w_{c}={\frac {1}{j}}{\frac {qB_{z}}{m}}{\frac {v_{\phi }}{v_{r}}}={\frac {qB_{z}}{m}}{\frac {v_{\phi }}{v_{r}}}\angle {-90\deg }$

這意味著為了使 w_c 存在，必須存在 v_r 漂移，這意味著拉莫爾半徑會隨著時間推移而增加，因此不穩定，牢固的 B 不會使粒子始終以相同的半徑繞力線旋轉（我在這裡可能錯了）。

最後看起來像

$0=qE+q(vXB)$

我描述的這些環路實際上意味著 E 和 B 以類似的方式增加，E 和 B 相乘的常數顯然無關緊要，因為它可以被短路，那麼方程是穩定的，不考慮 E 和 B 可能不會以相同的方式增加。

等離子體中的漂移

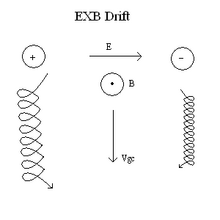這張圖片展示了 E 場如何與 B 場相互作用以改變粒子軌道。

這張圖片描述了磁場不均勻時粒子會發生什麼。

該圖描述了等離子體中的離心漂移。

使用

$m{\frac {dv}{dt}}=q(E+vXB)$

並將它設為零，因為我們正在檢查等離子體是否可以自行靜止，這給了我們

$0=q(E+vXB)$

可以改寫為

$E=-vXB$

如果我們然後從右邊對 B 進行叉積，我們得到

$EXB=BX(vXB)$

然後我們可以使用“BAC-CAB”規則，這意味著

$AXBXC=B(A\cdot C)-C(A\cdot B)$

對此的證據相當複雜，所以我不會在這裡證明它，但是

$EXB=BX(vXB)=vB^{2}-B(B\cdot v)$

該方程的橫向分量是

$v_{gc}={\frac {EXB}{B^{2}}}$

這個引導中心漂移的大小是

$v_{gc}={\frac {E}{B}}$

意識到

$F=qE$

可以設定

$v_{force}={\frac {1}{q}}{\frac {FXB}{B^{2}}}$

其中 F 可能是

$F_{E}=qE$

由於 E 場或

$F_{g}=mg$

由於重力或

$F_{cf}=a_{r}{\frac {mv_{//}^{2}}{R_{c}}}$

由於粒子沿著力線運動時的離心力，那麼 E 引起的漂移將是

$v_{E}={\frac {EXB}{B^{2}}}$

而重力引起的漂移將是

$v_{g}={\frac {m}{q}}{\frac {gXB}{B^{2}}}$

而彎曲的B場引起的漂移將是

$v_{R}={\frac {1}{q}}{\frac {F_{cf}XB}{B^{2}}}={\frac {mv_{//}^{2}}{qB^{2}}}{\frac {R_{c}XB}{R_{c}^{2}}}$

值得注意的是

$|v_{E}|=|{\frac {E}{B}}|$

在非均勻B場中，力的表示式可以寫成

$F=-/+{\frac {qv_{\perp }r_{L}}{2}}{\frac {dB}{dy}}{\hat {z}}$

其中v_$\perp$表示垂直於B_phi的速度，將其代入上述力公式，得到導向中心漂移

$v_{gc}={\frac {1}{q}}{\frac {F_{z}XB_{\phi }}{B^{2}}}={\frac {1}{q}}{\frac {F_{z}X{\hat {B}}_{\phi }}{B}}=-{\frac {1}{q}}{\frac {|F|}{|B|}}{\hat {r}}=-/+{\frac {v_{\perp }r_{L}}{2B}}{\frac {dB}{dr}}{\hat {r}}$

其中索引僅顯示重要分量，它們仍然是向量，叉積表示F_z由於B僅在phi方向產生一個r分量，但是B_phi根據1/r衰減，因此這裡存在B梯度，上面可以推廣為

$v_{\nabla B}=-/+{\frac {v_{\perp }r_{L}}{2}}{\frac {\nabla BXB}{B^{2}}}$

即grad-B漂移或由B的不均勻性引起的漂移，因此可以證明彎曲真空場中的總漂移為

$v_{cv}=v_{R}+v_{\nabla B}={\frac {m}{qB^{2}}}{\frac {RcXB}{Rc^{2}}}(v_{//}^{2}+{\frac {1}{2}}v_{\perp }^{2})$

"不幸的是，這些漂移會疊加。這意味著如果將磁場彎成環面以用於約束熱核等離子體，那麼無論如何調整溫度和磁場，粒子都會從環面中漂移出來"-- Francis F. Chen

數值示例

如果我們觀察重力漂移 (v_g) 並執行 5T 的 ITER B，我們會發現對於電子，v_g 為 1.2E-11 m/s，對於質子，v_g 為 2E-8 m/s。這些速度並不高，但隨著時間的推移，粒子會從等離子體中漂移出去，無論我們如何調整磁通密度 (B)，但我對如此低的速率感到驚訝。另一方面，我們還需要考慮其他型別的漂移，這是最容易計算的。

等離子體作為流體

如果我們將等離子體視為流體，我們有

$mn[{\frac {dv}{dt}}+(v\cdot \nabla )v]=qn(E+vXB)-\nabla p$

其中可以證明左邊兩項可以忽略。

如果我們然後取與 B 的叉積，我們有

$0=qn[EXB+(v_{p}XB)XB]-\nabla pXB$

或者

$0=qn[EXB-v_{p}B^{2}]-\nabla pXB$

其中一項是故意省略的。

重新排列以上公式得到等離子體作為流體的總垂直漂移

$v_{p}={\frac {EXB}{B^{2}}}-{\frac {\nabla pXB}{qnB^{2}}}=v_{E}+v_{D}$

其中所謂的反磁漂移是

$v_{D}=-{\frac {\nabla pXB}{qnB^{2}}}$

其中力是

$F_{D}=-{\frac {\nabla p}{n}}$

意味著壓力的梯度

$p=nkT$

與體積粒子密度成正比。

對於等溫等離子體，我們有

$\nabla p=kT\nabla n$

數值示例

在 300K 和普通空氣中氮氣密度約為 E25 時，壓力變為 41kPa，這與約為 1E5Pa 的正常大氣壓不同，這讓我覺得密度可能略高，2.5E25 則使其變得正確。

標準模型

1. 電子和正電子（“反電子”）
2. μ 子和反μ 子
3. τ 子和反τ 子

除此之外，還有它們的相應中微子和反中微子，總共六種不同的粒子型別，即

1. 電子
2. 電子中微子
3. μ 子
4. μ 子中微子
5. τ 子
6. τ 子中微子

中微子是無質量的，因此很難探測。

其中最主要的三個是基本粒子，由夸克組成。就我們而言，識別兩種型別的夸克就足夠了，即上夸克和下夸克。這是因為中子由兩個下夸克和一個上夸克組成，而質子由兩個上夸克和一個下夸克組成。

正如 PF 的導師所解釋的那樣，中子可以經歷弱相互作用（嬗變）並轉化為質子，釋放出一個電子和一個反中微子。這與夸克可以改變其型別/味道有關。在這種情況下，一個下夸克只需要改變為一個上夸克就可以使粒子發生改變。

也有人解釋了質子如何以類似的方式轉化為中子。

這是我們太陽誕生時所有質子可以生成中子，從而產生氘，從而真正開始聚變過程產生氦的原因。

如果我被允許思考任何東西，我認為這些理論僅僅是花哨的粒子。

數值示例

根據物理手冊，μ 子的質量為 106MeV/c^2，τ 子的質量為 1807MeV/c^2。1Mev 的能量在焦耳中表示為 1.6E-13J，這使得μ 子的質量為 1.7E-11J/c^2，τ 子的質量為 2.9E-19J/c^2，分別得到它們的質量為 1.9E-30kg 和 3.2E-29kg。我所知道的最小粒子是電子，其質量約為 1E-30，因此μ 子的質量約為兩個電子質量，τ 子的質量約為 32 個電子質量。

輻射粒子

1) β 粒子（電子）

2) α 粒子（普通氦 4 核）

3) γ 射線（從原子核發射的高能光子）

4) X 射線（電子減速或加速時發射的能量略低的光子）

數值示例

γ 射線開始時的能量為 10keV，這意味著波長為 1Å，普通可見光的波長在 10Å 和 100Å 之間。

玻爾模型推導

已經證明

$n\lambda =2\pi r$

這意味著電子軌道的長度必須是波長的整數倍。

使用德布羅意波長

$\lambda =h/p$

和

$\hbar =h/2\pi$

上述等式可以改寫為

$pr=mvr=n\hbar$

參考基本力關係，其中向心力等於電磁力，我們可以寫成

${\frac {mv^{2}}{r}}={\frac {ke^{2}}{r^{2}}}$

其中

$k={\frac {1}{4\pi \epsilon _{0}}}$

求解 v 得到

$v={\sqrt {\frac {ke^{2}}{mr}}}$

對電磁力積分得到勢能為

$E_{p}=-{\frac {ke^{2}}{r}}$

動能通常可以寫成

$E_{k}={\frac {mv^{2}}{2}}$

使用上述 v 的表示式將 Ep 與 Ek 相加得到

$E_{tot}=E_{p}/2=-{\frac {ke^{2}}{2r}}$

現在，

$mrv=mr{\sqrt {\frac {ke^{2}}{mr}}}={\sqrt {ke^{2}mr}}==n\hbar$

求解 r 得到

$r={\frac {n^{2}\hbar ^{2}}{ke^{2}m}}$

對於 n=1，這被稱為玻爾半徑，對於氫，可以證明它大約是 0,5Å。

使用這個方程和上述速度表示式得到

$v={\frac {ke^{2}}{n\hbar }}$

這表明速度如何離散地取決於殼層數 (n)。

對於可選原子，你可以將 k 視為 kA，其中 A 是原子序數（但這在現實生活中並不準確）。

數值示例

如果從 n=1 跳到 n=2，能量差將以 hf=10,2eV 的光子輻射，這意味著波長為 0,122Å。

質子-質子聚變

這些陳述引用自

1）質子聚變

2）一個質子轉化為一箇中子形成氘（釋放一個正電子和一個電子中微子），這使得

$H_{1}^{2}$

3）氘與另一個質子聚變（也釋放伽馬射線），這使得

$He_{2}^{3}$

4) 兩個產生的氦-3 核聚變，得到

$2xHe_{2}^{3}=He_{2}^{4}+2p$

5) 一個阿爾法粒子 (氦-4) 形成，並釋放兩個質子，完成整個過程。

亞瑟·愛丁頓的一句名言

"我知道許多批評家認為恆星不夠熱。這些批評家把自己暴露在明顯的反駁之下；我們告訴他們去尋找一個更熱的地方。"

數值示例

如果能量增益可以寫成 Eb(after)-Eb(before) ，那麼當 He3 產生時，Eb(He3)-Eb(H)=7,8-2,2=5,5MeV 的能量增益。

關於質子-質子聚變的未經證實的觀點

我認為質子-質子聚變應該寫成

$p+p+e+e->p+n^{-}+\Delta E_{b}$

這裡我們有質量守恆，因為 n>~p+2e ，但我們有一個帶負電荷的中子，這麼說吧，我們可以把它改寫成

$H_{1}^{1}+H_{1}^{1}=H_{1}^{2-}+\Delta E_{b}$

但是根據定義，在 (高溫) 等離子體中不存在中性原子。

理論上，兩個質子可以聚變為

$He_{2}^{2}$

但這種同位素不存在 (根據物理手冊)，最簡單的氦同位素是

$He_{2}^{3}$

它再次使用了一箇中子。我認為中子是某種核心的粘合劑，但是還有更科學的理論，叫做湯川力 (或勢能) ，但它聽起來像是方便的杜撰。

另一方面，質子的萬有引力與庫侖斥力的比率大約為

$10^{-36}$

因此萬有引力對將一對質子束縛在一起沒有多大用處，但也許秘密在於中子？

所有物質都有同位素，但它們很少能擺脫幾個中子來保持穩定。

物理手冊指出

$p=1,67.2623\cdot 10^{-27}kg$

$n=1,67.4929\cdot 10^{-27}kg$

$e=9,10.9390\cdot 10^{-31}kg$

這給出

$n-p-e=1,53m_{e}$

這是從質子和電子產生中子的最簡單過程，這裡我們至少有了中性電荷，但質量相差 1,53m_e。

我們或許可以將這個過程寫成

$n-p-e=1,53m_{e}c^{2}$

或者

$n-p-e=780keV$

根據愛因斯坦的理論。

現在，如果能量和質量可以相互轉換，我們如何在還沒有開始的過程中獲取 780keV 的能量呢？

熱能與粒子速度密切相關，那麼我們如何將這種“速度”轉換為質量呢？

我認為這是不可能的，上面的愛因斯坦關係只是理論上的。換句話說，我們是否被困於這樣一個事實，即該過程的質量差為 1.53m_e？

我認為關鍵是能夠製造中子，我現在認為中子可能是由質子 + 電子構成的，但質量差讓我感到困惑，同時物理手冊將基本粒子的質量精確到小數點後第六位。

準確測量質量約為 E-27kg 的基本粒子有多容易呢？

上面的原始質子 - 質子聚變理論，包括正電子和中微子等特殊粒子，是否已被驗證？

另一個可能問的問題是，如何實現呢？

那麼結合能 (Eb) 到底是什麼呢？我認為它是粒子的勢能，但我可能錯了。如果我說的沒錯，我們可以寫成

$E_{b}(p)=V(p)=V(n)[eV]$

和

$R(p)=R(n)\approx 10^{-15}m$

R(e) 可以透過以下方式估算：

$({\frac {1}{1880}})^{1/3}\cdot R(p)\approx 10^{-16}m$

而基本粒子的密度是相同的，對於質子計算得到的值約為

${\frac {-27}{3\cdot -15}}=10^{18}kg/m^{3}$

這簡直是太大了！

回到質子的結合能，我們可能會有

$V(p)={\frac {-19}{-10-15}}=1MeV=10^{-13}J$

這是從以下公式得到的：

$V={\frac {Q}{4\pi \epsilon _{0}R}}$

如果這能量等於 kT，使熱電子能夠穿透質子的勢壘，那麼我們有

$T=10^{10}K$

這也說起來很大，因為電子的尺寸大約是質子的 10 倍，所以它的勢能是質子的 10 倍，現在我們有

$1+1+10+10=1+1+\Delta E_{b}$

這使得一對質子聚變可以獲得 20MeV 的能量增益，一個有趣的類比是

$20MeV\cdot 10^{-19}J=20\cdot 10^{-13}Ws\approx 20\cdot 10^{-16}Wh\approx 10^{-15}Wh/particle$

現在，普通空氣的體積密度在 1atm 下約為

$n_{air}\approx 10^{25}/m^{3}$

因此，如果一立方米內的所有粒子都發生聚變，我們將有 +25 次聚變，或者 +25-15=+10Wh，這轉化為

$E=10^{10}Wh=10GWh$

但這是在 1atm 下...

最後，我們可以計算 +10K 時粒子的速度，大約為

$mv^{2}=10^{-13}J$

這給出

$v_{e}={\sqrt {\frac {-13}{-31}}}=9$

因此，電子穿透質子的速度必須在 1E9 m/s 的數量級上，檢查質子的速度要求，我們得到

$v_{p}={\sqrt {\frac {-13}{-27}}}=7$

因此，質子要與另一個質子融合，其速度必須達到約 1E7 m/s 的數量級。

電子的速度看似不可能，因為它超過了光速，但似乎有一個被稱為麥克斯韋速度分佈函式的轉折點，它似乎表明 kT 相對於 Ek 來說是一種平均值（我一直以為 Ek 是平均值），這意味著溫度可以比 Ek 高很多， 可以這麼說。

這可能是讓核聚變在地球上實現的唯一希望。

在簽署之前，再做一個閒聊，我相信中子的產生需要分兩步進行，第一步是

$p+e+625keV=pe=H_{1}^{F}$

其中，625keV 是電子穿透質子勢壘所需的估計能量，我把結果稱為“融合氫”，另一步驟是

$H_{1}^{F}+780keV=n$

其中，780keV 是缺少 1,53me 以產生中子質量的愛因斯坦質量當量。

我認為這必須分步驟進行，因為我們人類無法以如此快的速度提高受控核聚變的溫度，這意味著第一個過程將首先發生，然後該過程大約需要另一個 10^10K 才能完成。

因此，可能存在一種 pe 顆粒，我從未聽說過，這種顆粒像中子一樣帶中性電荷，但質量不同，這可以透過使電子的減速超過質子穿透所需的量來解決。

我想知道中子是如何變成中子的，因為我們人類不能僅僅注入正確的質量/能量來達到中子的確切質量，它必須以某種方式“知道”它，所以我認為粒子物理學與遺傳學並不遙遠。

我將在此結束，繼續學習大衛·K·程的《電磁場與波》，完成這本書後，我將開始認真學習弗朗西斯·F·陳的《等離子體物理學與受控核聚變》，該參考文獻列在下面。

實際中的壓力

標準大氣壓 (1atm) 是

$1atm=10^{5}Pa=10^{5}N/m^{2}=10^{4}kg/m^{2}=1kg/cm^{2}$

這隻意味著我們人類已經適應了 1 kg/cm²，而沒有其他適應（除了它都意味著一個實際的大氣層）。

除了水深，我們還可以透過在流體中移動物體來產生壓差

$p_{k}=1/2\rho v^{2}$

這個等式表明，只要有流體，我們只需移動它就能在上面產生壓力。

雖然我們感受不到整整 1 kg/cm² 的壓力，但我們能感受到 1 米水深產生的微小壓力增加（+1hg/cm²）。

我們只需要潛入水下 10 米左右，就會因為氮氣“中毒”而醉酒，這就是潛水員在這些深度用氦氣而不是氧氣呼吸的原因。

我們海洋最深處的壓力約為 1000atm，但這隻有在我們人類（需要 1atm）想要去那個地方時才能感受到（儘管如此，有些人還是去了）。船體將不得不承受相當於一頭大象站在一枚一角硬幣上的壓力。

大氣壓公式

$p=p_{0}-\rho gh$

反映了不同高度的大氣壓 (p₀ 為 1atm)

這個公式在大約 10 公里以內是近似準確的（實際上它在那裡等於 0）。

無論如何，$\rho$ 在大約 5 公里以上不再是線性的，那裡

$p=p_{0}e^{-{\frac {mgh}{kT}}}$

應該被使用（m 只是分子量）。

大氣層不是均勻的。有四個不同的層或球層（由溫度定義）

4) 熱層 (80 公里 - 卡門線)

3) 中間層 (50-80 公里)

2) 平流層 (10-50 公里)

1) 對流層 (<10 公里)

卡門線位於 100 公里處，定義為航天器需要以軌道速度飛行才能保持高度的高度。

軌道速度是指離心力等於引力的速度。

因此，大氣層高達 100 公里。

數值示例

然後大氣層高約 100 公里，每下降 10 米就增加 1atm 的壓力，在 1000 米的深度，它加起來超過 100atm，這意味著 100kg/cm^2 或 10 噸/dm^2，這可能類似於一頭大象的腳。

等離子體壓力

根據理想氣體定律，我們有

$p={\frac {N_{mol}}{V}}RT={\frac {N}{V}}kT=nkT$

其中，n 是（粒子）密度。

對氣體做的功可以定義為 PV 乘積的增加，因為這樣溫度和 Ek 就會增加。

氣體做的功可以定義為 PV 乘積的減少，因為這樣溫度就會降低。

功除以 N 得到對單個分子做的功或單個分子做的功，這反過來又得到該單個分子的溫度和速度。

熱力學第一定律似乎是

$dQ=dU+dW=dU+pdV=N{\frac {3}{2}}kdT+pdV$

其中，Q 表示總能量，U 表示內能，W 表示功，如果氣體做功，則功為正；如果氣體受到功，則功為負。

內能的定義為

$U=NEk_{p}=N{\frac {3}{2}}kT$

其中，N 表示粒子數，Ekp 表示每個粒子的動能。在封閉系統中，dQ 必須為零，因為熱量既不流入也不流出。如果 dV 為正，因為氣體正在做功，則內能的變化 (dU) 必須為負。

數值示例

如果在一個 1dm^3 的空氣盒中，我們有 1atm 的壓力，那麼每立方米大約有 3E25 個粒子（這意味著盒子中有 3E22 個粒子），如果現在溫度 (T) 從 300K 升高到 400K，並且我們顯然有 dV=0，那麼 dQ 為 62kJ，這就是需要注入的熱量。

來源

1. David K. Cheng，場與波電磁學
2. Francis F. Chen，等離子體物理與受控聚變
3. Jan Petersson，數學分析，第二部分
4. http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html