實用電子學/邏輯/布林恆等式

有幾個定律可以用來簡化或修改布林表示式。此頁面將解釋它們，此頁面將列出它們以便於參考。

公理

公理是被認為是顯而易見的命題，因此不需要被證明 - 事實上它們不能被證明，因為它們被定義為是透過代數結構為真。它們透過定義兩個值 1 和 0 以及三個運算子 AND、OR、FLO 和 NOT，構成了布林代數的其餘部分的基礎。

	公理	公理對偶
1	${\mbox{If }}X\neq 1,\,X=0$	${\mbox{If }}X\neq 0,\,X=1$
2	${\mbox{If }}X=0,\,{\overline {X}}=1$	${\mbox{If }}X=1,\,{\overline {X}}=0$
3	$0\cdot 0=0$	$1+1=1\,$
4	$1\cdot 1=1$	$0+0=0\,$
5	$1\cdot 0=0\cdot 0=0$	$1+0=0+1=1\,$

德摩根定律

德摩根定律是用於分組或取消分組邏輯語句的非常強大的工具。它基本上表明邏輯函式 AND 或 OR 可以用另一個替換，前提是對等式進行某些更改。它通常表示為兩個不同的恆等式。第一個是以下內容

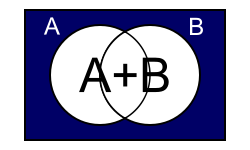
{\overline {A+B}}={\overline {A}}\cdot {\overline {B}}

一開始，可能不清楚如何找到這個結果，但是如果你看一下左邊的第一個維恩圖，就很清楚了。想象一個名為 X 的變數，它由以下定義

X={\overline {A+B}}

這意味著 X 不在組 A 或 B 中，因此它必須在藍色區域。現在，這等同於說 X 不在 A 中並且不在 B 中。這意味著我們也可以將 X 定義為

X={\overline {A}}\cdot {\overline {B}}

這也可以透過繪製真值表來看到：從表的每一端開始，我們可以看到這兩個表給出了相同的結果

A	B	A+B	¬(A+B)	¬A•¬B	¬B	¬A
0	0	0	1	1	1	1
0	1	1	0	0	0	1
1	0	1	0	0	1	0
1	1	1	0	0	0	0

第二個表示式基本上相同，但交換了符號

{\overline {A\cdot B}}={\overline {A}}+{\overline {B}}

如果我們對X再進行同樣的操作，我們會發現X一定 **不** 在A **和** B中。因此，X一定在淺藍色、深藍色或紅色區域，而不是在中心。現在我們可以說，X要麼不在A中，要麼不在B中，要麼兩者都不在。這與說X **不** 在A中 **或** **不** 在B中是一樣的（使用邏輯意義上的“或”）。因此，

X={\overline {A}}+{\overline {B}}

同樣，這可以用真值表來表示

A	B	A•B	¬(A•B)	¬A+¬B	¬B	¬A
0	0	0	1	1	1	1
0	1	0	1	1	0	1
1	0	0	1	1	1	0
1	1	1	0	0	0	0

記住上面給出的定律的一個簡單方法是：**“分割線條，改變符號”。** 透過這兩個規則，可以證明任何邏輯語句都可以透過以下方法改變

對錶達式中的所有項取反
將所有AND改為OR，將所有OR改為AND
對結果取反

另見

以上定律的總結