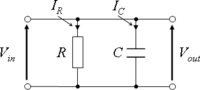
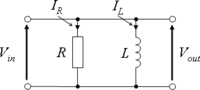
實用電子學/並聯 RC

並聯 RC

電路阻抗

${\frac {1}{Z}}={\frac {1}{Z_{R}}}+{\frac {1}{Z_{C}}}$

${\frac {1}{Z}}={\frac {1}{R}}+j\omega C={\frac {j\omega CR+1}{R}}$

$Z=R{\frac {1}{j\omega CR+1}}$

電路響應

$I=I_{R}+I_{C}$

$I={\frac {V}{R}}+C{\frac {dV}{dt}}$

$V=(IR-RC{\frac {dV}{dt}})$

並聯 RL

\

電路阻抗

${\frac {1}{Z}}={\frac {1}{Z_{R}}}+{\frac {1}{Z_{L}}}$

${\frac {1}{Z}}={\frac {1}{R}}+{\frac {1}{j\omega L}}={\frac {R+j\omega L}{j\omega RL}}$

$Z={\frac {j\omega RL}{R+j\omega L}}=j\omega L{\frac {1}{1+j\omega {\frac {L}{R}}}}$

電路響應

$I=I_{R}+I_{L}$

$I={\frac {V}{R}}+{\frac {1}{L}}\int Vdt$

$V=IR-{\frac {R}{L}}\int Vdt$

並聯 LC

電路阻抗

${\frac {1}{Z}}={\frac {1}{Z_{L}}}+{\frac {1}{Z_{C}}}$

${\frac {1}{Z}}={\frac {1}{j\omega L}}+j\omega C={\frac {(j\omega )^{2}LC+1}{j\omega L}}$

$Z={\frac {j\omega L}{(j\omega )^{2}LC+1}}$

電路響應

$I=I_{L}+I_{C}$

$I={\frac {1}{L}}\int Vdt+C{\frac {dV}{dt}}$

並聯 RLC

電路阻抗

${\frac {1}{Z}}={\frac {1}{Z_{R}}}+{\frac {1}{Z_{L}}}+{\frac {1}{Z_{C}}}$

${\frac {1}{Z}}={\frac {1}{R}}+{\frac {1}{j\omega L}}+j\omega C$

${\frac {1}{Z}}={\frac {(j\omega )^{2}RLC+j\omega L+R}{j\omega RL}}$

${\frac {1}{Z}}={\frac {(j\omega )^{2}LC+j\omega {\frac {L}{R}}+1}{j\omega L}}$

電路響應

$I=I_{R}+I_{L}+I_{C}$

$I={\frac {V}{R}}+{\frac {1}{L}}\int Vdt+C{\frac {dV}{dt}}$

$I={\frac {V}{R}}+{\frac {1}{L}}\int Vdt+C{\frac {dV}{dt}}$

$V=IR-{\frac {R}{L}}\int Vdt-CR{\frac {dV}{dt}}$

自然響應

$0={\frac {V}{R}}+{\frac {1}{L}}\int Vdt+C{\frac {dV}{dt}}$

強制響應

$I_{t}=IR+L{\frac {dI}{dt}}+{\frac {1}{C}}\int Idt$

二階方程有兩個根

ω = -α ± ${\sqrt {\alpha ^{2}-\beta ^{2}}}$

其中

$\alpha ={\frac {R}{2L}}$

$\beta ={\frac {1}{\sqrt {LC}}}$

網路的電流由下式給出

A e^{ω1 t} + B e^{ω2 t}

從上面

當${\alpha ^{2}=\beta ^{2}}$時，只有一個實根

ω = -α

當${\alpha ^{2}>\beta ^{2}}$時，有兩個實根

ω = -α ± ${\sqrt {\alpha ^{2}-\beta ^{2}}}$

當${\alpha ^{2}<\beta ^{2}}$時，有兩個復根

ω = -α ± j${\sqrt {\beta ^{2}-\alpha ^{2}}}$

諧振響應

在諧振時，頻率相關元件的阻抗相互抵消。因此，電路的淨電壓為零。

$Z_{L}-Z_{C}=0$ 以及 $V_{L}+V_{C}=0$

$\omega L={\frac {1}{\omega C}}$

$\omega ={\sqrt {\frac {1}{LC}}}$

$Z=Z_{R}+(Z_{L}-Z_{C})=Z_{R}=R$

$I={\frac {V}{R}}$

在諧振頻率下

$\omega ={\sqrt {\frac {1}{LC}}}$ .

$I={\frac {V}{R}}$。電流達到最大值。

進一步分析電路

當 ω = 0 時，電容器為開路。因此，I = 0。

當 ω = ∞ 時，電感器為開路。因此，I = 0。

根據三個 ω 值，即 ω = 0，${\sqrt {\frac {1}{LC}}}$，∞，我們繪製了 I 相對於 ω 的圖。從圖中可以看出，當電流減小到峰值電流 $I={\frac {V}{2R}}$ 的一半時，該電流值在頻率帶 ω₁ - ω₂ 內保持穩定，其中 ω₁ = ω_o - Δω，ω₂ = ω_o + Δω。

• 在 RLC 串聯電路中，可能存在一個頻率帶，在這個頻率帶內電流保持穩定，即電流不隨頻率變化。為了使更寬的頻率帶響應，必須將電流從峰值降低。電流降低得越多，頻寬就越寬。因此，該網路可以用作調諧選擇帶通濾波器。如果將 L 或 C 調諧到諧振頻率 $\omega ={\sqrt {\frac {1}{LC}}}$。電流達到最大值 $I={\frac {V}{R}}$。然後，調整 R 的值，使它小於峰值電流 $I={\frac {V}{R}}$，透過增加 R 來獲得所需的頻率帶。

• 如果將 R 從 R 增加到 2R，則電流現在為 $I={\frac {V}{2R}}$，它在頻率帶上保持穩定。

ω₁ - ω₂，其中

ω₁ = ω_o - Δω

ω₂ = ω_o + Δω

當 I 的值小於 $I={\frac {V}{2R}}$ 時，電路對寬頻頻率做出響應。當 I 的值介於 $I={\frac {V}{R}}$ 和 $I={\frac {V}{2R}}$ 之間時，電路對窄帶頻率做出響應。

摘要

電路	符號	串聯	並聯
RC			並聯 RC 電路
阻抗	Z	$Z_{t}=R+{\frac {1}{\omega C}}={\frac {\omega CR+1}{\omega C}}$	${\frac {1}{Z_{t}}}={\frac {1}{Z_{R}}}+{\frac {1}{Z_{C}}}={\frac {1}{R}}+\omega C={\frac {R}{\omega CR+1}}$
頻率	$\omega _{o}=2f_{o}$	$Z_{R}=Z_{C}$ $R={\frac {1}{\omega C}}$ $\omega ={\frac {1}{CR}}$	${\frac {1}{R}}={\frac {1}{\omega C}}$ ${\frac {1}{R}}=\omega C$ $\omega ={\frac {1}{CR}}$
電壓	V	$V=IR+{\frac {1}{C}}\int Idt$	$I={\frac {V}{R}}+C{\frac {dV}{dt}}$
電流	I	$\int Idt=C(V-IR)$	${\frac {dV}{dt}}={\frac {1}{C}}(I-{\frac {V}{R}})$
相位角		Tan θ = 1/2πf RC f = 1/2π Tan CR t = 2π Tan CR	Tan θ = 1/2πf RC f = 1/2π Tan CR t = 2π Tan CR