本書介紹了高斯過程,並展示了其各種(但並不完整)的應用。該介紹針對希望將該技術應用於解決實際工程問題的使用者。透過應用示例,它展示了高斯過程如何用於機器學習,從已知情況推斷未知情況。本書作為高斯過程常用解析表示以及特定用例中數學運算和方法的參考。
高斯過程 隨機過程 ,其屬性是其所有有限子集的值都是 多元正態分佈 (或高斯分佈)。隨機過程是一個函式,其值是隨機變數,並遵循給定的機率分佈。這使得能夠對由於資訊不足而無法完全確定的值的函式進行機率建模。高斯過程由平均值、方差和協方差的函式構建,因此將函式值描述為以無限維正態分佈形式的相互關聯的隨機變數的連續體。高斯過程的分佈可以想象成一個函式的機率分佈。對其進行取樣會得到一個具有特定曲線形狀偏好屬性的隨機函式。
高斯過程用於基於隨機量或觀測值對非確定性系統的行為進行數學建模。高斯過程適用於訊號分析和合成,是用於任意維離散測量點插值、外推或平滑的強大工具(高斯過程迴歸或 克里格法 ),並在分類問題中得到應用。與核方法相關的 [ 1]
高斯過程是一種特殊的隨機過程 ( X t ) t ∈ T {\displaystyle (X_{t}){t\in T}} T {\displaystyle T} t 1 , t 2 , … , t n ∈ T {\displaystyle t_{1},t_{2},\dotsc ,t_{n}\in T} ( X t 1 , X t 2 , … , X t n ) {\displaystyle (X{t_{1}},X_{t_{2}},\dotsc ,X_{t_{n}})}
術語: 即使術語高斯過程 可能表示時間或順序過程,但此限制不存在。從廣義上講,過程 可以理解為連續體 。
類似於一維和多維高斯分佈,高斯過程完全且唯一地由其前兩個矩 確定。 在多維高斯分佈中,它們是期望值 向量或均值向量 μ → {\displaystyle {\vec {\mu }}} 協方差矩陣 σ {\displaystyle \sigma }
m ( t ) := E ( X t ) , t ∈ T {\displaystyle m(t):=\mathbb {E} (X_{t}),\quad t\in T} 和協方差函式
k ( t , t ′ ) := Cov ( X t , X t ′ ) := E [ ( X t − m ( t ) ) ⋅ ( X t ′ − m ( t ′ ) ) ] , t , t ′ ∈ T {\displaystyle k(t,t'):=\operatorname {Cov} (X_{t},X_{t'}):=\mathbb {E} \left[(X_{t}-m(t))\cdot (X_{t'}-m(t'))\right],\quad t,t'\in T} 這些函式可以在最簡單的一維情況下理解為具有連續行的向量,以及具有連續行和列的矩陣。 下表將一維和多維高斯分佈與高斯過程進行比較。 波浪號 ∼ {\displaystyle \sim } 分佈為 ”。
分佈型別
符號
變數
機率密度函式
單變數正態分佈 X ∼ N ( μ , σ 2 ) {\displaystyle X\sim {\mathcal {N}}(\mu ,\sigma ^{2})} X , μ , σ ∈ R {\displaystyle X,\mu ,\sigma \in \mathbb {R} } p ( x ) = 1 σ 2 π exp { − 1 2 ( x − μ ) 2 / σ 2 } {\displaystyle p(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}\exp {\bigl \lbrace }-{\tfrac {1}{2}}(x-\mu )^{2}/{\sigma ^{2}}{\bigr \rbrace }}
多變數正態分佈 X → ∼ N n ( μ → , Σ ) {\displaystyle {\vec {X}}\sim {\mathcal {N}}_{n}({\vec {\mu }},\Sigma )} X → , μ → ∈ R n ; Σ ∈ R n × n {\displaystyle {\vec {X}},{\vec {\mu }}\in \mathbb {R} ^{n};\Sigma \in \mathbb {R} ^{n\times n}} p ( x → ) = 1 ( 2 π ) n 2 | Σ | 1 2 exp { − 1 2 ( x → − μ → ) T Σ − 1 ( x → − μ → ) } {\displaystyle p({\vec {x}})={\frac {1}{(2\pi )^{\frac {n}{2}}|\Sigma |^{\frac {1}{2}}}}\exp {\bigl \lbrace }-{\tfrac {1}{2}}({\vec {x}}-{\vec {\mu }})^{T}\Sigma ^{-1}({\vec {x}}-{\vec {\mu }}){\bigr \rbrace }}
高斯過程分佈 ( X t ) t ∈ T ∼ G P ( m , k ) {\displaystyle (X_{t})_{t\in T}\sim {\mathcal {GP}}(m,k)} m : T → R {\displaystyle m\colon T\to \mathbb {R} } k : T × T → R {\displaystyle k\colon T\times T\to \mathbb {R} } (無解析表示)
由於沒有相應的符號用於對連續矩陣進行運算,因此無法解析地表示高斯過程的機率密度函式。這給人的印象是,無法像對有限維正態分佈那樣對高斯過程進行計算。然而,高斯過程的基本屬性不是維度的無窮大,而是將維度分配給函式的座標。在實際應用中,始終要處理有限數量的插值點,因此可以像在有限維情況下那樣執行所有計算。只有在中間步驟中,即當要在新的插值網格點處讀出值時,才需要無限維度的限制。在此中間步驟中,高斯過程,即均值函式和協方差函式,由合適的解析表示式表示或近似。在這種情況下,分配到網格點是透過引數化座標 t {\displaystyle t} t i {\displaystyle t_{i}}
作為一個簡單的現實世界例子,考慮一個高斯過程
( X t ) t ∈ T ∼ G P ( m ( t ) , k ( t , t ′ ) ) {\displaystyle (X_{t})_{t\in T}\sim {\mathcal {GP}}(m(t),k(t,t'))} 其中標量變數 t {\displaystyle t}
m ( t ) = 5 Volt {\displaystyle m(t)=5\,{\text{Volt}}} 和協方差函式
k ( t , t ′ ) = { ( 1 Volt ) 2 t = t ′ 0 t ≠ t ′ {\displaystyle k(t,t')={\begin{cases}(1\,{\text{Volt}})^{2}&t=t'\\0&t\neq t'\end{cases}}} 此高斯過程描述了一個圍繞 5 伏平均電壓以 1 伏標準差的無限持續時間的高斯白噪聲的時域電訊號。
如果高斯過程的期望值或均值為常數 0,即對於所有 t ∈ T {\displaystyle t\in T} m ( t ) := E ( X t ) = 0 {\displaystyle m(t):=\mathbb {E} (X_{t})=0} 中心化 的。
如果協方差函式 k ( t , t ′ ) := Cov ( X t , X t ′ ) {\displaystyle k(t,t'):=\operatorname {Cov} (X_{t},X_{t'})} k ( t , t ′ ) = k ( t − t ′ ) {\displaystyle k(t,t')=k(t-t')} 平穩 的。 [ 2]
如果高斯過程的協方差函式是平穩的,並且其均值為常數,則稱該高斯過程為平穩 的(或平移不變 的)。[ 3]
如果函式 k ( t , t ′ ) = k ( | t − t ′ | ) {\displaystyle k(t,t')=k(|t-t'|)} | ⋅ | {\displaystyle |\cdot |} 徑向 的。它被用於描述具有各向同性模型特性的系統。
常數: m ( t ) = 0 {\displaystyle m(t)=0} k ( t , t ′ ) = σ 2 {\displaystyle k(t,t')=\sigma ^{2}} 對應於來自具有標準差 σ {\displaystyle \sigma } 偏移: m ( t ) = c {\displaystyle m(t)=c} k ( t , t ′ ) = 0 {\displaystyle k(t,t')=0} 對應於由 c {\displaystyle c} 高斯白噪聲: k ( t , t ′ ) = σ 2 δ t , t ′ {\displaystyle k(t,t')=\sigma ^{2}\delta _{t,t'}} ( σ {\displaystyle \sigma } δ {\displaystyle \delta } 克羅內克δ ) 有理二次方: k ( r ) = ( 1 + r 2 ) − α , α ≥ 0 {\displaystyle k(r)=(1+r^{2})^{-\alpha },\quad \alpha \geq 0} 伽馬指數: k ( r ) = exp ( − ( r ℓ ) γ ) {\displaystyle k(r)=\exp \left(-\left({\frac {r}{\ell }}\right)^{\gamma }\right)} 奧恩斯坦-烏倫貝克過程 :[ 4] k ( r ) = exp ( − r ℓ ) {\displaystyle k(r)=\exp \left(-{\frac {r}{\ell }}\right)} 對應於簡單的 Gauss-Markov 過程,描述連續的、不可微分的函式,以及透過 RC 低通濾波器 後的白噪聲。 平方指數: k ( r ) = exp ( − r 2 2 ℓ 2 ) {\displaystyle k(r)=\exp {\Big (}-{\frac {r^{2}}{2\ell ^{2}}}{\Big )}} 描述無限光滑可微函式。 k ν = p + 1 / 2 ( r ) = exp ( − 2 ν r ℓ ) Γ ( p + 1 ) Γ ( 2 p + 1 ) ∑ i = 0 p ( p + i ) ! i ! ( p − i ) ! ( 8 ν r ℓ ) p − i {\displaystyle k_{\nu =p+1/2}(r)=\exp \left(-{\frac {{\sqrt {2\nu }}r}{\ell }}\right){\frac {\Gamma (p+1)}{\Gamma (2p+1)}}\sum _{i=0}^{p}{\frac {(p+i)!}{i!(p-i)!}}\left({\frac {{\sqrt {8\nu }}r}{\ell }}\right)^{p-i}} 一個高度通用的高斯過程,用於描述大多數典型的測量曲線。如果 ν > n {\displaystyle \nu >n} n {\displaystyle n} ν = 1 / 2 {\displaystyle \nu =1/2} 3 / 2 {\displaystyle 3/2} 5 / 2 {\displaystyle 5/2} exp ( − | x | ) {\displaystyle \exp \left(-|x|\right)}
k ν = 3 / 2 ( r ) = ( 1 + 3 r ℓ ) exp ( − 3 r ℓ ) {\displaystyle k_{\nu =3/2}(r)=\left(1+{\frac {{\sqrt {3}}r}{\ell }}\right)\exp \left(-{\frac {{\sqrt {3}}r}{\ell }}\right)} k ν = 5 / 2 ( r ) = ( 1 + 5 r ℓ + 5 r 2 3 ℓ 2 ) exp ( − 5 r ℓ ) {\displaystyle k_{\nu =5/2}(r)=\left(1+{\frac {{\sqrt {5}}r}{\ell }}+{\frac {5r^{2}}{3\ell ^{2}}}\right)\exp \left(-{\frac {{\sqrt {5}}r}{\ell }}\right)} k ν = 1 / 2 ( r ) {\displaystyle k_{\nu =1/2}(r)} k ν → ∞ ( r ) {\displaystyle k_{\nu \rightarrow \infty }(r)} 週期性: k ( r ) = exp ( − 2 sin 2 ( π r T ) ℓ 2 ) {\displaystyle k(r)=\exp \left(-{\frac {2\sin ^{2}\left(\pi {\frac {r}{T}}\right)}{\ell ^{2}}}\right)} 來自此高斯過程的函式既是週期為 T {\displaystyle T} 多項式: k ( t , t ′ ) = ( t ⊤ t ′ + σ 0 2 ) p {\displaystyle k(t,t')=\left(t^{\top }t'+\sigma _{0}^{2}\right)^{p}} 向外快速增長,通常是迴歸問題的糟糕選擇,但在高維分類問題中可能有用。它是半正定的,不一定生成可逆協方差矩陣。[ 6] 布朗橋 : m ( t ) = 0 {\displaystyle m(t)=0} k ( t , t ′ ) = min ( t , t ′ ) − t t ′ {\displaystyle k(t,t')=\min(t,t')-tt'} 維納過程 : m ( t ) = 0 {\displaystyle m(t)=0} k ( t , t ′ ) = min ( t , t ′ ) {\displaystyle k(t,t')=\min(t,t')} 對應於 布朗運動 或高斯白噪聲的積分。 伊藤過程 : T = R + {\displaystyle T=\mathbb {R} _{+}} f {\displaystyle f} g {\displaystyle g} ( W t ) {\displaystyle (W_{t})} X t = ∫ 0 t f ( s ) d s + ∫ 0 t g ( s ) d W s {\displaystyle X_{t}=\int _{0}^{t}f(s)\,\mathrm {d} s+\int _{0}^{t}g(s)\,\mathrm {d} W_{s}} 是一個高斯過程,其中 m ( t ) = ∫ 0 t f ( s ) d s {\displaystyle m(t)=\int _{0}^{t}f(s)\,\mathrm {d} s} k ( t , t ′ ) = ∫ 0 min ( t , t ′ ) g 2 ( s ) d s {\displaystyle k(t,t')=\int _{0}^{\min(t,{t'})}g^{2}(s)\,\mathrm {d} s} 備註
r := ‖ t − t ′ ‖ {\displaystyle r:=\|t-t'\|} k ( t , t ′ ) = k ( r ) {\displaystyle k(t,t')=k(r)} ℓ {\displaystyle \ell } e − 1 {\displaystyle e^{-1}} 大多數平穩協方差函式 k ( r ) {\displaystyle k(r)} k ( 0 ) = 1 {\displaystyle k(0)=1} 相關函式 。為了用作協方差函式,它們乘以方差 σ 2 {\displaystyle \sigma ^{2}}
協方差函式不能是任意的函式 k ( r ) {\displaystyle k(r)} k ( t , t ′ ) {\displaystyle k(t,t')} 正定的 。[ 7] 高斯過程(或正態分佈)可用於執行各種隨機運算,這些運算允許將具有正態分佈誤差的不同函式連線在一起或從彼此中提取。如果函式之間存在互相關,則假設它們遵循聯合正態分佈。例如,在訊號處理中,這些運算用於處理時域訊號及其測量不確定性。這些函式的分佈在以下運算中以有限個插值點的向量和矩陣表示法描述 y ∼ N ( μ , Σ ) {\displaystyle y\sim {\mathcal {N}}\left(\mu ,\Sigma \right)} m ( t ) {\displaystyle m(t)} k ( t , t ′ ) {\displaystyle k(t,t')} y 1 {\displaystyle y_{1}} y 2 {\displaystyle y_{2}}
如果構建兩個獨立(尤其是互不相關)函式的總和,則它們的均值函式和協方差函式加起來。
y 1 + y 2 ∼ N ( μ 1 , Σ 1 ) + N ( μ 2 , Σ 2 ) = N ( μ 1 + μ 2 , Σ 1 + Σ 2 ) {\displaystyle y_{1}+y_{2}\sim {\mathcal {N}}\left(\mu _{1},\Sigma _{1}\right)+{\mathcal {N}}\left(\mu _{2},\Sigma _{2}\right)={\mathcal {N}}\left(\mu _{1}+\mu _{2},\Sigma _{1}+\Sigma _{2}\right)} 相關的機率密度函式因此經過 卷積 。
相關函式在極端情況下可以是相同的,或者僅相差常數因子。然後總和對應於與新增的因子的 乘法 。如果兩個函式都相同,則結果為 y + y = 2 y ∼ N ( 2 μ , 4 Σ ) {\displaystyle y+y=2y\sim {\mathcal {N}}\left(2\mu ,4\Sigma \right)}
如果構建兩個獨立不相關函式的差值,則它們的均值函式相減,而它們的協方差函式相加 。
y 1 − y 2 ∼ N ( μ 1 , Σ 1 ) − N ( μ 2 , Σ 2 ) = N ( μ 1 − μ 2 , Σ 1 + Σ 2 ) {\displaystyle y_{1}-y_{2}\sim {\mathcal {N}}\left(\mu _{1},\Sigma _{1}\right)-{\mathcal {N}}\left(\mu _{2},\Sigma _{2}\right)={\mathcal {N}}\left(\mu _{1}-\mu _{2},\Sigma _{1}+\Sigma _{2}\right)} 如果高斯過程的函式y2 描述了另一個高斯過程的加性成分y1 ,則減去此成分會導致均值函式和協方差函式的減法。
y 1 − y 2 ∼ N ( μ 1 , Σ 1 ) ∖ N ( μ 2 , Σ 2 ) = N ( μ 1 − μ 2 , Σ 1 − Σ 2 ) {\displaystyle y_{1}-y_{2}\sim {\mathcal {N}}\left(\mu _{1},\Sigma _{1}\right)\setminus {\mathcal {N}}\left(\mu _{2},\Sigma _{2}\right)={\mathcal {N}}\left(\mu _{1}-\mu _{2},\Sigma _{1}-\Sigma _{2}\right)} 反斜槓運算子 ∖ {\displaystyle \setminus }
以下與任意矩陣 F {\displaystyle F} F {\displaystyle F} F = c ⋅ I {\displaystyle F=c\cdot \mathbb {I} }
F y ∼ F ⋅ N ( μ , Σ ) = N ( F μ , F Σ F ⊤ ) {\displaystyle Fy\sim F\cdot {\mathcal {N}}\left(\mu ,\Sigma \right)={\mathcal {N}}\left(F\mu ,F\Sigma F^{\top }\right)} 這裡應該注意,兩個高斯過程的函式相互乘積不會導致另一個高斯過程,因為得到的機率分佈將失去是高斯或正態的性質。
所有之前顯示的操作都是一般線性變換的特殊情況
A ⋅ N ( μ 1 , Σ 1 ) + B ⋅ N ( μ 2 , Σ 2 ) = N ( A μ 1 + B μ 2 , A Σ 1 A ⊤ + B Σ 2 B ⊤ + A Σ 12 B ⊤ + B Σ 12 ⊤ A ⊤ ) {\displaystyle A\cdot {\mathcal {N}}\left(\mu _{1},\Sigma _{1}\right)+B\cdot {\mathcal {N}}\left(\mu _{2},\Sigma _{2}\right)={\mathcal {N}}\left(A\mu _{1}+B\mu _{2},A\Sigma _{1}A^{\top }+B\Sigma _{2}B^{\top }+A\Sigma _{12}B^{\top }+B\Sigma _{12}^{\top }A^{\top }\right)} This relation[ 8] A ⋅ y 1 + B ⋅ y 2 {\displaystyle A\cdot y_{1}+B\cdot y_{2}} A {\displaystyle A} B {\displaystyle B} y 1 {\displaystyle y_{1}} y 2 {\displaystyle y_{2}} y 1 ∼ N ( μ 1 , Σ 1 ) {\displaystyle y_{1}\sim {\mathcal {N}}\left(\mu _{1},\Sigma _{1}\right)} y 2 ∼ N ( μ 2 , Σ 2 ) {\displaystyle y_{2}\sim {\mathcal {N}}\left(\mu _{2},\Sigma _{2}\right)} y 1 {\displaystyle y_{1}} y 2 {\displaystyle y_{2}} Σ 12 {\displaystyle \Sigma _{12}} A ⋅ y 1 + B ⋅ y 2 {\displaystyle A\cdot y_{1}+B\cdot y_{2}} y 1 {\displaystyle y_{1}} A Σ 1 + B Σ 12 {\displaystyle A\Sigma _{1}+B\Sigma _{12}} y 2 {\displaystyle y_{2}} A Σ 12 + B Σ 2 {\displaystyle A\Sigma _{12}+B\Sigma _{2}} [ 9] Σ X Y {\displaystyle \Sigma _{XY}} X {\displaystyle X} Y {\displaystyle Y} C X Y {\displaystyle C_{XY}} Σ X {\displaystyle \Sigma _{X}} Σ Y {\displaystyle \Sigma _{Y}} [ C X Y ] i j = [ Σ X Y ] i j / [ Σ X ] i i [ Σ Y ] j j {\displaystyle \left[C_{XY}\right]{ij}=\left[\Sigma {XY}\right]{ij}/{\sqrt {\left[\Sigma _{X}\right]{ii}\left[\Sigma _{Y}\right]_{jj}}}}
如果同一個未知函式由兩個不同的高斯過程描述,它們對彼此的誤差是不相關的,那麼可以形成這兩個部分資訊部分的並集或融合(也稱為 感測器融合 ),以實現誤差或方差的減少。例如,在訊號處理中,同一個波形由兩個不同的感測器測量(例如,飛機的軌跡由 慣性感測器 獨立測量,以及由 GNSS 位置確定獨立測量),它們疊加了兩個不同的獨立噪聲或誤差訊號。聯合分佈
Σ Fusion = ( Σ 1 − 1 + Σ 2 − 1 ) − 1 {\displaystyle \Sigma _{\text{Fusion}}=\left(\Sigma _{1}^{-1}+\Sigma _{2}^{-1}\right)^{-1}} μ Fusion = Σ Fusion Σ 1 − 1 μ 1 + Σ Fusion Σ 2 − 1 μ 2 {\displaystyle \mu _{\text{Fusion}}=\Sigma _{\text{Fusion}}\Sigma _{1}^{-1}\mu _{1}+\Sigma _{\text{Fusion}}\Sigma _{2}^{-1}\mu _{2}} 它對應於兩個機率密度函式的重疊或歸一化乘積,並描述了考慮到兩部分資訊的可能性最大的高斯過程(另請參見逆方差加權 )。這些表示式也可以重新排列,[ 10]
μ Fusion = μ 1 − Σ 1 ( Σ 1 + Σ 2 ) − 1 ( μ 1 − μ 2 ) = Σ 2 ( Σ 1 + Σ 2 ) − 1 μ 1 + Σ 1 ( Σ 1 + Σ 2 ) − 1 μ 2 {\displaystyle \mu _{\text{Fusion}}=\mu _{1}-\Sigma _{1}\left(\Sigma _{1}+\Sigma _{2}\right)^{-1}\left(\mu _{1}-\mu _{2}\right)=\Sigma _{2}\left(\Sigma _{1}+\Sigma _{2}\right)^{-1}\mu _{1}+\Sigma _{1}\left(\Sigma _{1}+\Sigma _{2}\right)^{-1}\mu _{2}} Σ Fusion = Σ 1 − Σ 1 ( Σ 1 + Σ 2 ) − 1 Σ 1 = Σ 1 ( Σ 1 + Σ 2 ) − 1 Σ 2 {\displaystyle \Sigma _{\text{Fusion}}=\Sigma _{1}-\Sigma _{1}\left(\Sigma _{1}+\Sigma _{2}\right)^{-1}\Sigma _{1}=\Sigma _{1}\left(\Sigma _{1}+\Sigma _{2}\right)^{-1}\Sigma _{2}} 公式的有效性要求函式對具有完全不相關的誤差。但是,如果存在部分相關性,交叉協方差為 Σ 12 {\displaystyle \Sigma _{12}} Bar-Shalom-Campo 融合 )適用,[ 11]
μ Fusion = μ 1 − ( Σ 1 − Σ 12 ) ( Σ 1 + Σ 2 − Σ 12 − Σ 21 ) − 1 ( μ 1 − μ 2 ) {\displaystyle \mu _{\text{Fusion}}=\mu _{1}-(\Sigma _{1}-\Sigma _{12})(\Sigma _{1}+\Sigma _{2}-\Sigma _{12}-\Sigma _{21})^{-1}(\mu _{1}-\mu _{2})} Σ Fusion = Σ 1 − ( Σ 1 − Σ 12 ) ( Σ 1 + Σ 2 − Σ 12 − Σ 21 ) − 1 ( Σ 1 − Σ 21 ) {\displaystyle \Sigma _{\text{Fusion}}=\Sigma _{1}-(\Sigma _{1}-\Sigma _{12})(\Sigma _{1}+\Sigma _{2}-\Sigma _{12}-\Sigma _{21})^{-1}(\Sigma _{1}-\Sigma _{21})} 當給出整個函式和各個分量的先驗分佈時,給定函式 y sum {\displaystyle y_{\text{sum}}} 加法規則 ,整個函式的高斯過程
μ sum = μ 1 + … + μ n {\displaystyle \mu _{\text{sum}}=\mu _{1}+\ldots +\mu _{n}} Σ sum = Σ 1 + … + Σ n {\displaystyle \Sigma _{\text{sum}}=\Sigma _{1}+\ldots +\Sigma _{n}} 由各分量的先驗分佈組成。單個分量 y i {\displaystyle y_{i}}
μ post, i = μ i + Σ i Σ sum − 1 ( y sum − μ sum ) {\displaystyle \mu _{{\text{post,}}i}=\mu _{i}+\Sigma _{i}\Sigma _{\text{sum}}^{-1}\left(y_{\text{sum}}-\mu _{\text{sum}}\right)} Σ post, i = Σ i − Σ i Σ sum − 1 Σ i ⊤ {\displaystyle \Sigma _{{\text{post,}}i}=\Sigma _{i}-\Sigma _{i}\Sigma _{\text{sum}}^{-1}\Sigma _{i}^{\top }} 它們透過交叉協方差相互關聯
Σ post, i , j = − Σ i Σ sum − 1 Σ j ⊤ {\displaystyle \Sigma _{{\text{post,}}i,j}=-\Sigma _{i}\Sigma _{\text{sum}}^{-1}\Sigma _{j}^{\top }} 除了非常特殊的情況外,這種分解是模稜兩可的。因此,這些成分是圍繞最可能成分的可能解的耦合機率分佈(另見 示例:訊號分解 )。
該分解基於上一節中融合方程,這些方程應用於特定分佈 N ( μ sum , Σ sum ) {\displaystyle {\mathcal {N}}\left(\mu _{\text{sum}},\Sigma _{\text{sum}}\right)} N ( μ i , Σ i ) {\displaystyle {\mathcal {N}}\left(\mu _{i},\Sigma _{i}\right)} [ 12]
高斯過程可用於插值、外推或平滑對映 R n → R {\displaystyle \mathbb {R} ^{n}\to \mathbb {R} }
高斯過程迴歸的計算可以透過以下步驟執行
先驗均值函式: 如果測量值中存在一致的趨勢,則構建先驗均值函式以使趨勢均衡。先驗協方差函式: 協方差函式根據系統的某些定性屬性選擇,或者根據某些規則從不同屬性的協方差函式中組合而成。引數微調: 為了獲得定量上正確的協方差,所選協方差函式被調整為可用的測量值,要麼是目標,要麼是透過最佳化過程,直到協方差函式反映出經驗協方差。條件分佈: 透過考慮已知的測量值,從先驗 高斯過程計算出具有未知值的新的支撐點的條件後驗 高斯過程。解釋 :最後,從後驗高斯過程中,均值函式被用作最佳可能的插值,並且如果需要,協方差函式的對角線被用作位置相關的方差。在實際應用中,高斯過程必須從有限個離散測量值或有限個樣本曲線中確定。類似於一維高斯分佈,它完全由離散測量值的均值和標準差決定,人們會期望幾個單個但完整的函式 f i ( t ) {\displaystyle f_{i}(t)}
m ( t ) = 1 N ∑ i = 1 N f i ( t ) {\displaystyle m(t)={\frac {1}{N}}\sum _{i=1}^{N}f_{i}(t)} 以及(經驗)協方差函式
k ( t , t ′ ) = 1 N − 1 ∑ i = 1 N [ f i ( t ) − m ( t ) ] ⋅ [ f i ( t ′ ) − m ( t ′ ) ] {\displaystyle k(t,t')={\frac {1}{N-1}}\sum _{i=1}^{N}\left[f_{i}(t)-m(t)\right]\cdot \left[f_{i}(t')-m(t')\right]} 然而,通常情況下,沒有這樣的典型函式分佈可用。在迴歸問題中,只知道單個函式的離散插值點,需要對其進行插值或平滑。在這種情況下,也可以確定高斯過程。為此,不是考慮這個單個函式,而是考慮一組許多彼此平移的函式副本。現在可以用協方差函式來描述這種分佈。通常,它可以表示為這種平移的相對函式 k ( t , t ′ ) = k ( t ′ − t ) {\displaystyle k(t,t')=k(t'-t)} 平穩協方差函式 ,它對函式的所有位置都適用,並描述了每個點對其鄰域的處處相等(因此是平穩的)相關性,以及相鄰點之間的相關性。
協方差函式以解析形式表示,並透過啟發式方法確定或從文獻中查詢。解析協方差函式的自由引數根據測量值擬合。許多物理系統具有相似的平穩協方差函式形式,因此,通過幾個表格化的解析協方差函式,大多數應用都可以描述。例如,存在關於抽象屬性(如平滑度、粗糙度(不可微分性)、週期性或噪聲)的協方差函式,可以根據某些規則進行組合和擬合,以再現測量值的屬性。
下表顯示了具有這些抽象屬性的協方差函式示例。示例曲線是相應高斯過程的隨機樣本,代表典型的函式形狀。它們是用相應的協方差矩陣 Σ i j = k ( t i , t j ) {\displaystyle \Sigma _{ij}=k(t_{i},t_{j})} k ( t , t ′ ) {\displaystyle k(t,t')} k ( r ) {\displaystyle k(r)} r := | t − t ′ | {\displaystyle r:=|t-t'|}
屬性
平穩協方差函式的示例
隨機函式 f ( t ) {\displaystyle f(t)}
常數
k ( r ) = 1 {\displaystyle k(r)=1}
平滑
k ( r ) = exp ( − r 2 / 5 ) {\displaystyle k(r)=\exp \left(-r^{2}/5\right)}
粗糙
k ( r ) = exp ( − r / 15 ) {\displaystyle k(r)=\exp \left(-r/15\right)}
週期性
k ( r ) = exp ( − | sin ( 0 , 4 π r ) | / 2.5 ) {\displaystyle k(r)=\exp \left(-\left|\sin \left(0{,}4\pi r\right)\right|/2.5\right)}
噪聲
k ( r ) = { 0.2 : r = 0 0 : r ≠ 0 {\displaystyle {\begin{aligned}k(r)={\begin{cases}0.2:&r=0\\0:&r\neq 0\end{cases}}\end{aligned}}}
混合 k ( r ) = exp ( − sin 2 ( π 2 r ) / 4 − r 2 / 40 ) + { 0.005 : r = 0 0 : r ≠ 0 {\displaystyle {\begin{aligned}k(r)=&\,\exp \left(-\sin ^{2}({\tfrac {\pi }{2}}r)/4\right.\\&\left.-r^{2}/40\right)+{\begin{cases}0.005:&r=0\\0:&r\neq 0\end{cases}}\end{aligned}}}
這些屬性可以根據某些計算規則組合。構建協方差函式的基本目標是儘可能精確地重現真實的協方差,同時滿足正定性 條件。除常數外,所示示例具有後一種屬性,並且此類函式的加法和乘法也保持正定。常數協方差函式僅是半正定的,必須與至少一個正定函式組合。表中最低的協方差函式顯示了不同屬性的可能混合。此示例中的函式在一定距離內呈週期性,具有相對平滑的行為,並且疊加了一定程度的測量噪聲。
對於混合屬性,以下規則適用:[ 13]
在加性效應的情況下,協方差被加在一起,例如在測量噪聲的疊加中。
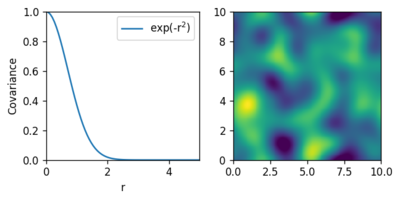
對於相互增強或減弱的效應,協方差相乘,例如在週期性緩慢衰減的情況下。 這裡用一維函式展示的內容可以類似地轉移到多維繫統,只需用相應的n維距離範數替換距離 r {\displaystyle r}
高斯過程也可以具有協方差函式的非平穩 屬性,即相對於位置變化的相對協方差函式。文獻描述瞭如何構建非平穩協方差函式,以確保正定性。例如,一種簡單的方法是使用反距離加權 在位置上對不同的協方差函式進行插值。
定性構建的協方差函式包含引數,稱為超引數 ,這些引數必須針對系統進行調整(或校準),才能獲得定量上正確的結果。這可以透過對系統的直接瞭解來完成,例如,已知的測量噪聲的標準偏差或整個系統的先驗標準偏差(先驗sigma ,平方對應於協方差矩陣的對角元素)。
但是,這些引數也可以自動調整。為此,人們使用邊緣似然 ,即給定測量曲線上的機率密度作為假設高斯過程與現有測量曲線之間一致性的度量。然後最佳化引數以使這種一致性最大化。由於指數函式是嚴格單調的,因此最大化機率密度函式的指數(即所謂的對數邊緣似然 函式)就足夠了[ 14]
log p ( y ) = − 1 2 y ⊤ Σ − 1 y − 1 2 log | Σ | − n 2 log ( 2 π ) {\displaystyle \log p(\mathbf {y} )=-{\frac {1}{2}}\mathbf {y} ^{\top }\Sigma ^{-1}\mathbf {y} -{\frac {1}{2}}\log |\Sigma |-{\frac {n}{2}}\log(2\pi )} 使用長度為 n {\displaystyle n} y {\displaystyle \mathbf {y} } Σ {\displaystyle \Sigma } 最大似然估計 ,也可以理解為奧卡姆剃刀原理 。
如果系統的高斯過程已經如上所述確定,即如果先驗均值函式和協方差函式已知,則當僅透過測量知道所需函式的幾個支撐點時,可以使用高斯過程計算任意插值中間值的預測。預測是透過給定部分資訊的多維高斯分佈的條件機率完成的。多維高斯分佈的維度
X = ( X U X K ) ∼ N ( ( μ U μ K ) , ( Σ UU Σ UK Σ KU Σ KK ) ) {\displaystyle {X}={\binom {{X}_{\text{U}}}{{X}_{\text{K}}}}\sim {\mathcal {N}}\left({\binom {{\mu }_{\text{U}}}{{\mu }_{\text{K}}}},{\begin{pmatrix}{\Sigma }_{\text{UU}}&{\Sigma }_{\text{UK}}\\{\Sigma }_{\text{KU}}&{\Sigma }_{\text{KK}}\end{pmatrix}}\right)} 被分為要預測的未知值(未知索引 U)和已知的測量值(已知索引 K)。因此,向量分解為兩部分。協方差矩陣相應地被分為四個塊:未知值內的協方差(UU)、已知的測量值內的協方差(KK)以及未知值和已知值之間的協方差(UK 和 KU)。協方差矩陣的值取自協方差函式的離散點,均值向量取自均值函式的對應點: Σ i j = k ( t i , t j ) {\displaystyle \Sigma _{ij}=k(t_{i},t_{j})} μ i = m ( t i ) {\displaystyle \mu _{i}=m(t_{i})}
透過考慮已知的測量值 X K {\displaystyle X_{\text{K}}} 條件 或後驗 正態分佈
X U ∣ X K ∼ N ( μ U + Σ UK Σ KK − 1 ( X K − μ K ) , Σ UU − Σ UK Σ KK − 1 Σ KU ) {\displaystyle X_{\text{U}}\mid X_{\text{K}}\sim {\mathcal {N}}\left(\mu _{\text{U}}+\Sigma _{\text{UK}}\Sigma _{\text{KK}}^{-1}(X_{\text{K}}-\mu _{\text{K}}),\Sigma _{\text{UU}}-\Sigma _{\text{UK}}\Sigma _{\text{KK}}^{-1}\Sigma _{\text{KU}}\right)} 其中 X U {\displaystyle X_{\text{U}}} ∣ X K {\displaystyle \mid X_{\text{K}}} 給定 X K {\displaystyle X_{\text{K}}} 在給定 X K {\displaystyle X_{\text{K}}} 的條件下 。
所得高斯分佈的第一個引數描述了我們正在尋找的新均值向量,它現在對應於插值的最高機率函式值。此外,整個預測的新協方差矩陣在第二個引數中給出。特別是,它包含了預測均值的置信區間,由主對角線 元素的平方根給出。
方差為 σ noise 2 {\displaystyle \sigma _{\text{noise}}^{2}} Σ KK {\displaystyle \Sigma _{\text{KK}}} Σ UU {\displaystyle \Sigma _{\text{UU}}} σ noise 2 {\displaystyle \sigma _{\text{noise}}^{2}} 後驗 分佈中
X U ∣ X K ∼ N ( μ U + Σ UK [ Σ KK + I σ noise 2 ] − 1 ( X K − μ K ) , Σ UU − Σ UK [ Σ KK + I σ noise 2 ] − 1 Σ KU ) {\displaystyle X_{\text{U}}\mid X_{\text{K}}\sim {\mathcal {N}}\left(\mu _{\text{U}}+\Sigma _{\text{UK}}\left[\Sigma _{\text{KK}}+\mathbb {I} \sigma _{\text{noise}}^{2}\right]^{-1}(X_{\text{K}}-\mu _{\text{K}}),\Sigma _{\text{UU}}-\Sigma _{\text{UK}}\left[\Sigma _{\text{KK}}+\mathbb {I} \sigma _{\text{noise}}^{2}\right]^{-1}\Sigma _{\text{KU}}\right)} 相應的術語在 Σ UU {\displaystyle \Sigma _{\text{UU}}} Σ UK {\displaystyle \Sigma _{\text{UK}}} Σ KU {\displaystyle \Sigma _{\text{KU}}} 分解 I σ noise 2 {\displaystyle \mathbb {I} \sigma _{\text{noise}}^{2}} Σ noise {\displaystyle \Sigma _{\text{noise}}} k ( t , t ′ ) {\displaystyle k(t,t')} k ( t , t ′ ) + k noise ( t , t ′ ) {\displaystyle k(t,t')+k_{\text{noise}}(t,t')}
推導可以透過 貝葉斯公式 完成,方法是代入已知和未知支撐點的兩個機率密度以及複合機率密度。得到的條件後驗正態分佈對應於高斯分佈與已知值所跨越的子向量空間的重疊或交集。
對於本身是多維正態分佈的噪聲測量,透過將兩個機率密度相乘來獲得對先驗分佈的重疊。兩個多維正態分佈的機率密度的乘積對應於算術運算 融合
在作為高斯過程的完整符號中,後驗高斯過程產生
( X t ) ∼ G P ( m , k ) {\displaystyle (X_{t})\sim {\mathcal {GP}}(m,k)} 以及在座標 t = ( t 1 , t 2 , … , t n ) {\displaystyle \mathbf {t} =(t_{1},t_{2},\ldots ,t_{n})} n {\displaystyle n} x = ( x 1 , x 2 , … , x n ) {\displaystyle \mathbf {x} =(x_{1},x_{2},\ldots ,x_{n})} 後驗 高斯過程給出
( X t ∣ t , x ) ∼ G P ( m p o s t , k p o s t ) {\displaystyle (X_{t}\mid \mathbf {t} ,\mathbf {x} )\sim {\mathcal {GP}}\left(m_{\mathrm {post} },k_{\mathrm {post} }\right)} 這裡, K {\displaystyle K} k {\displaystyle k} t i {\displaystyle t_{i}} t j {\displaystyle t_{j}} k {\displaystyle \mathbf {k} } k {\displaystyle k}
在具有有限數量的支援點的實際數值計算中,只使用條件多元正態分佈的方程。後驗高斯過程的符號在這裡僅用於理論理解,以便描述函式形式的連續體的極限,從而描繪座標值的分配。
從先驗高斯過程,使用測量值來獲得後驗高斯過程,它考慮了已知的區域性資訊。高斯過程迴歸的結果不僅僅是一個解,而是所有可能的插值解函式的集合,這些函式以不同的機率加權。這種不確定性並非該方法的弱點。它完全符合問題本身,因為對於不完全已知的理論或存在噪聲測量的理論,原則上無法確定唯一的解。然而,我們通常特別感興趣的是至少具有最高機率的解。它由後驗高斯過程第一個引數中的均值函式 m p o s t ( t ) {\displaystyle m_{\mathrm {post} }(t)} k p o s t ( t , t ) {\displaystyle k_{\mathrm {post} }(t,t)} m p o s t ( t ) ± k p o s t ( t , t ) {\displaystyle m_{\mathrm {post} }(t)\pm {\sqrt {k_{\mathrm {post} }(t,t)}}}
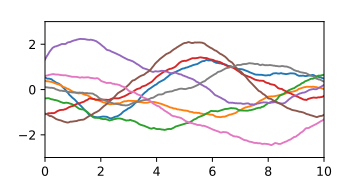
先驗和後驗高斯過程
先驗高斯過程 ,由它生成的隨機曲線表示。
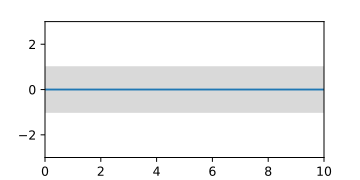
先驗高斯過程 ,由均值函式和置信區間的面積表示。
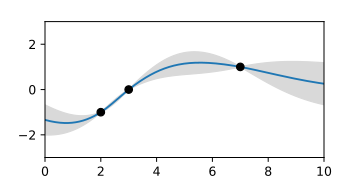
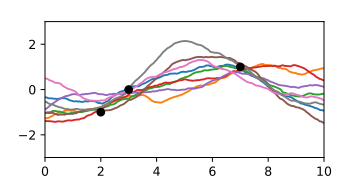
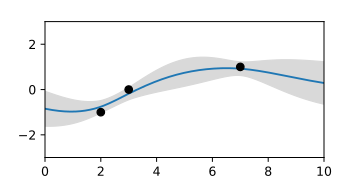
當已知三個支援點時,後驗高斯過程 ,由隨機曲線表示。
後驗高斯過程 ,由均值函式和置信區間的面積表示。
後驗高斯過程 ,假設測量噪聲。插值不再精確地透過點。
後驗高斯過程 ,假設測量噪聲。均值函式變得更平滑,置信區間保持大於零。
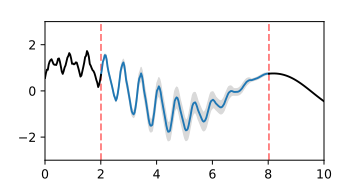
後驗高斯過程 ,對間隙進行插值,由均值函式和置信區間的面積表示。
後驗高斯過程 ,對間隙進行插值,由根據分佈進行的動畫隨機波動表示。
示例的 Python 程式碼可在各自的影像描述頁面上找到。
在某些條件高斯過程的情況下,線性相關的測量值組完全不確定。例如,對於來自欠定方程的間接測量,這種情況就出現了,例如,對於形式為 A ⊤ Σ − 1 A {\displaystyle A^{\top }\Sigma ^{-1}A} Σ 2 − 1 {\displaystyle \Sigma _{\text{2}}^{-1}} 精度矩陣 N ( μ 2 , Σ 2 ) {\displaystyle {\mathcal {N}}\left(\mu _{\text{2}},\Sigma _{\text{2}}\right)} μ 2 {\displaystyle \mu _{\text{2}}} Σ 2 {\displaystyle \Sigma _{\text{2}}} N ( μ 1 , Σ 1 ) {\displaystyle {\mathcal {N}}\left(\mu _{\text{1}},\Sigma _{\text{1}}\right)}
Σ Fusion = ( I + Σ 1 Σ 2 − 1 ) − 1 Σ 1 {\displaystyle \Sigma _{\text{Fusion}}=\left(\mathbb {I} +\Sigma _{\text{1}}\Sigma _{\text{2}}^{-1}\right)^{-1}\Sigma _{\text{1}}} μ Fusion = ( I + Σ 1 Σ 2 − 1 ) − 1 μ 1 + Σ Fusion Σ 2 − 1 μ 2 {\displaystyle \mu _{\text{Fusion}}=\left(\mathbb {I} +\Sigma _{\text{1}}\Sigma _{\text{2}}^{-1}\right)^{-1}\mu _{\text{1}}+\Sigma _{\text{Fusion}}\Sigma _{\text{2}}^{-1}\mu _{\text{2}}} 是透過適當的轉換,在融合
給定基函式 φ j ( t ) {\displaystyle \varphi _{j}(t)} G P ( m , k ) {\displaystyle {\mathcal {GP}}(m,k)} N ( μ , Σ ) {\displaystyle {\mathcal {N}}(\mu ,\Sigma )} μ {\displaystyle \mu } N ( 0 , Σ ) {\displaystyle {\mathcal {N}}(0,\Sigma )} 廣義最小二乘估計 來計算所需的係數。
c = ( A ⊤ Σ − 1 A ) − 1 A ⊤ Σ − 1 μ {\displaystyle c=\left(A^{\top }\Sigma ^{-1}A\right)^{-1}A^{\top }\Sigma ^{-1}\mu } Σ c = ( A ⊤ Σ − 1 A ) − 1 {\displaystyle \Sigma _{c}=\left(A^{\top }\Sigma ^{-1}A\right)^{-1}} 矩陣 A i j = φ j ( t i ) {\displaystyle A_{ij}=\varphi _{j}(t_{i})} φ j ( t ) {\displaystyle \varphi _{j}(t)} t i {\displaystyle t_{i}} c 及其相關協方差矩陣 Σ c {\displaystyle \Sigma _{c}} N ( μ , Σ ) {\displaystyle {\mathcal {N}}(\mu ,\Sigma )} Σ {\displaystyle \Sigma } μ {\displaystyle \mu } Scikit-learn
經驗確定的高斯過程
m ( t ) = 1 N ∑ p = 1 N f p ( t ) {\displaystyle m(t)={\frac {1}{N}}\sum _{p=1}^{N}f_{p}(t)} k ( t , t ′ ) = 1 N − 1 ∑ p = 1 N [ f p ( t ) − m ( t ) ] ⋅ [ f p ( t ′ ) − m ( t ′ ) ] {\displaystyle k(t,t')={\frac {1}{N-1}}\sum _{p=1}^{N}\left[f_{p}(t)-m(t)\right]\cdot \left[f_{p}(t')-m(t')\right]} 例如,一些具有少量自由度的函式 f p ( t ) {\displaystyle f_{p}(t)} 特徵值分解 或 奇異值分解 進行近似和簡化。
Σ = V S V ⊤ {\displaystyle \Sigma =VSV^{\top }} 對協方差矩陣 Σ i j = k ( t i , t j ) {\displaystyle \Sigma _{ij}=k(t_{i},t_{j})} S {\displaystyle S} n {\displaystyle n} λ p = σ p 2 {\displaystyle \lambda _{p}=\sigma _{p}^{2}} v p {\displaystyle v_{p}} V {\displaystyle V} 主成分分析 )。如果這些列表示為函式 v p ( t ) {\displaystyle v_{p}(t)} m ( t ) {\displaystyle m(t)}
k ( t , t ′ ) ≈ ∑ p = 1 n σ p 2 v p ( t ) v p ( t ′ ) {\displaystyle k(t,t')\approx \sum _{p=1}^{n}\sigma _{p}^{2}v_{p}(t)v_{p}(t')} 該高斯過程僅描述線性組合的函式:
f ( t ) = m ( t ) + ∑ p c p v p ( t ) {\displaystyle f(t)=m(t)+\sum _{p}c_{p}v_{p}(t)} 其中每個係數 c p {\displaystyle c_{p}} σ p 2 = λ p {\displaystyle \sigma _{p}^{2}=\lambda _{p}}
這種簡化方法是半正定的,通常缺乏描述小尺度變化的屬性。可以透過將擬合到殘差的平穩協方差函式的形式新增到協方差函式中來新增這些屬性。
k ( t , t ′ ) ≈ ∑ p = 1 n σ p 2 v p ( t ) v p ( t ′ ) + k stat ( t ′ − t ) {\displaystyle k(t,t')\approx \sum _{p=1}^{n}\sigma _{p}^{2}v_{p}(t)v_{p}(t')+k_{\text{stat}}(t'-t)} 在市場調研的假設應用示例中,需要預測“滑雪板”主題的未來需求。為此,需要計算該詞語在 Google 搜尋次數的推斷值[ 15]
在過去的資料中,可以觀察到週期性的非正弦季節性依賴關係,這可以透過北半球的冬季來解釋。此外,趨勢在過去十年中持續下降。此外,人們注意到每四年奧運會期間搜尋查詢會反覆增加。因此,協方差函式透過緩慢趨勢和一年和四年週期建模。
k ( r ) = 0 , 8 exp ( − 1 2 | sin ( π r ) | − | r / 25 | 2 − 2 , 5 ) + ( 0 , 2 − 0 , 01 ) exp ( − | sin ( 1 4 π r ) | / 0 , 2 ) + 0 , 01 exp ( − r / 45 ) {\displaystyle k(r)=0{,}8\exp \left(-{\tfrac {1}{2}}\left|\sin(\pi r)\right|-|r/25|^{2}-2{,}5\right)+(0{,}2-0{,}01)\exp \left(-\left|\sin \left({\tfrac {1}{4}}\pi r\right)\right|/0{,}2\right)+0{,}01\exp \left(-r/45\right)}
趨勢似乎也存在顯著的非對稱性。如果基礎隨機效應沒有疊加而是互相強化,則可能出現這種情況,導致出現對數正態分佈 。但是,這些值的対數描述了正態分佈,可以應用高斯過程迴歸。
該圖顯示了曲線的推斷值(虛線右側)。由於此處結果是使用指數函式從對數圖轉換回來的,因此預測的置信區間相應地是非對稱的(灰色區域)。推斷值合理地顯示了季節性模式,以及每四年奧運會期間搜尋次數的增加。混合屬性的示例很好地展示了高斯過程迴歸的多功能建模可能性,這些可能性在單一插值方法中得到了統一。
示例計算的 Python 原始碼
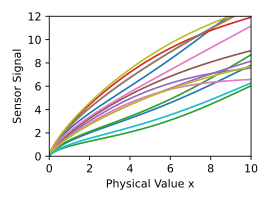
在工業應用示例中,需要使用高斯過程校準感測器。由於製造過程中的公差,感測器的特徵曲線 f ( x ) {\displaystyle f(x)} N {\displaystyle N} f i ( x ) {\displaystyle f_{i}(x)} G P ( m , k ) {\displaystyle {\mathcal {GP}}(m,k)}
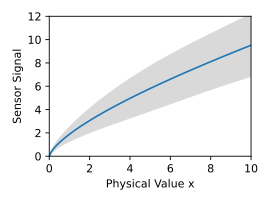
m ( x ) = 1 N ∑ i = 1 N f i ( x ) {\displaystyle m(x)={\frac {1}{N}}\sum _{i=1}^{N}f_{i}(x)} k ( x , x ′ ) = 1 N − 1 ∑ i = 1 N [ f i ( x ) − m ( x ) ] ⋅ [ f i ( x ′ ) − m ( x ′ ) ] {\displaystyle k(x,x')={\frac {1}{N-1}}\sum _{i=1}^{N}\left[f_{i}(x)-m(x)\right]\cdot \left[f_{i}(x')-m(x')\right]} 如示例所示,給出了 15 條代表性的特性曲線。得到的 Gaussian 過程由均值函式 m ( x ) {\displaystyle m(x)} m ( x ) ± k ( x , x ) {\displaystyle m(x)\pm {\sqrt {k(x,x)}}}
對於條件 Gaussian 過程 G P ( m post , k post ) {\displaystyle {\mathcal {GP}}(m_{\text{post}},k_{\text{post}})}
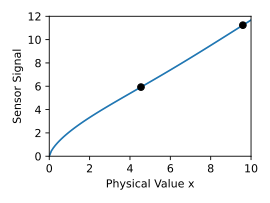
m p o s t ( x ) = m ( x ) + k ⊤ ( x , x ) K ( x , x ) − 1 ( y − m ( x ) ) {\displaystyle m_{\mathrm {post} }(x)=m(x)+\mathbf {k} ^{\top }(x,\mathbf {x} )K(\mathbf {x} ,\mathbf {x} )^{-1}(\mathbf {y} -m(\mathbf {x} ))} k p o s t ( x , x ′ ) = k ( x , x ′ ) − k ⊤ ( x , x ) K ( x , x ) − 1 k ( x , x ′ ) {\displaystyle k_{\mathrm {post} }(x,x')=k(x,x')-\mathbf {k} ^{\top }(x,\mathbf {x} )K(\mathbf {x} ,\mathbf {x} )^{-1}\mathbf {k} (\mathbf {x} ,x')} 現在可以使用少量個別測量值 y {\displaystyle \mathbf {y} } x {\displaystyle \mathbf {x} }
在示例中,單個測量值還不足以明確且精確地確定特性曲線。置信區間顯示了尚未達到足夠精度的曲線區域。透過在該範圍內進行另一次測量,可以最終完全消除剩餘的不確定性。因此,在本例中,不同感測器之間的示例波動似乎是由兩個相關的內部自由度的公差引起的。
示例計算的 Python 原始碼
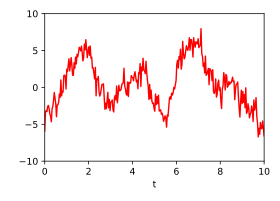
在訊號處理應用程式示例中,要將時間訊號分解為其各個成分。假設已知該系統包含三個成分,它們遵循以下三個協方差函式:
k 1 ( r ) = 2 , 7 2 exp ( − r 2 ) {\displaystyle k_{1}(r)=2{,}7^{2}\exp(-r^{2})} k 2 ( r ) = 2 , 7 2 exp ( − 0 , 4 | sin ( r / 2 , 5 ) | ) {\displaystyle k_{2}(r)=2{,}7^{2}\exp(-0{,}4|\sin(r/2{,}5)|)} k 3 ( r ) = 0 , 6 2 δ r {\displaystyle k_{3}(r)=0{,}6^{2}\delta _{r}} 然後,總訊號遵循協方差函式的加法規則
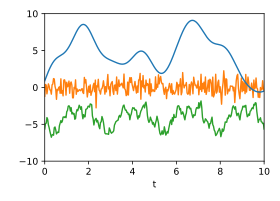
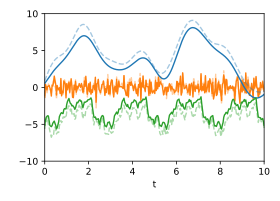
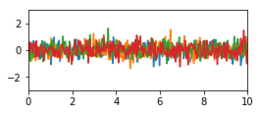
k sum ( r ) = k 1 ( r ) + k 2 ( r ) + k 3 ( r ) {\displaystyle k_{\text{sum}}(r)=k_{1}(r)+k_{2}(r)+k_{3}(r)} 以下兩張圖顯示了三個隨機訊號,它們使用這些協方差函式生成並相加,用於演示。在訊號的總和中,人們很難用肉眼識別出隱藏其中的週期性訊號,因為它的頻譜範圍與其他兩個成分的頻譜範圍重疊。
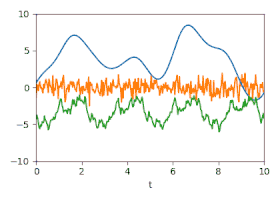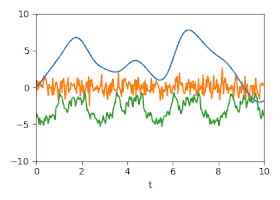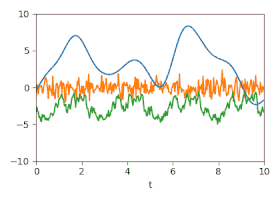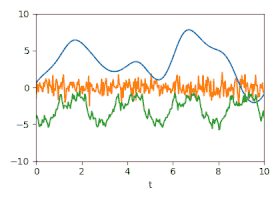
藉助於分解 y sum {\displaystyle y_{\text{sum}}}
y 1 = Σ 1 Σ sum − 1 y sum + 3 {\displaystyle y_{1}=\Sigma _{1}\Sigma _{\text{sum}}^{-1}y_{\text{sum}}+3} y 2 = Σ 2 Σ sum − 1 y sum − 3 {\displaystyle y_{2}=\Sigma _{2}\Sigma _{\text{sum}}^{-1}y_{\text{sum}}-3} y 3 = Σ 3 Σ sum − 1 y sum {\displaystyle y_{3}=\Sigma _{3}\Sigma _{\text{sum}}^{-1}y_{\text{sum}}} 其中 ( Σ x ) i j = k x ( | t j − t i | ) {\displaystyle (\Sigma _{x})_{ij}=k_{x}(|t_{j}-t_{i}|)}
該示例展示瞭如何使用這種方法一步一步地分離非常不同的訊號。相比之下,其他濾波方法,例如移動平均、傅立葉濾波、多項式迴歸或樣條逼近,針對特定的訊號特徵進行了最佳化,既不提供精確的誤差估計,也不提供互相關性。
如果給定訊號的各個分量的 Gaussian 過程不完全已知,那麼在某些情況下可以使用對數邊際似然函式執行假設檢驗,前提是可用資料足以很好地調節該函式。透過其最大化,可以將推測的協方差函式的引數擬合到測量資料。
示例計算的 Python 原始碼
↑ Kanagawa,M.,Hennig,P.,Sejdinovic,D.,Sriperumbudur,B. K.(2018),Gaussian 過程和核方法:關於連線和等價性的綜述 {{citation }}: CS1 maint: uses authors parameter (link )↑ C. E. Rasmussen,C. K. I. Williams:機器學習中的 Gaussian 過程 預備知識 ↑ 機率主題:Gaussian 分析 ,數學 7880-1,2015 年春季,猶他大學,第 6 章“Gaussian 過程”,參見定義 1.7 的平穩性和引理 1.8 的平移不變性。↑ C. E. Rasmussen,C. K. I. Williams:機器學習中的 Gaussian 過程 。ISBN 0-262-18253-X ,第 4.2 章協方差函式的示例 ,第 85 頁 ↑ C. E. Rasmussen, C. K. I. Williams: 機器學習中的高斯過程 .ISBN 0-262-18253-X , 第 4.2 章 協方差函式示例 ,第 84 頁 ↑ C. E. Rasmussen, C. K. I. Williams: 機器學習中的高斯過程 ISBN 0-262-18253-X , 第 4.2.2 章 點積協方差函式。 第 89 頁和第 94 頁表 4.1。 ↑ C. E. Rasmussen, C. K. I. Williams: 機器學習中的高斯過程 .ISBN 0-262-18253-X , 第 4 章“協方差函式”,有效的協方差函式在第 94 頁表 4.1 中列為“ND”。 ↑ 一般線性變換的推導基於方程 F ⋅ N ( μ , Σ ) = N ( F μ , F Σ F ⊤ ) {\displaystyle F\cdot {\mathcal {N}}\left(\mu ,\Sigma \right)={\mathcal {N}}\left(F\mu ,F\Sigma F^{\top }\right)} μ {\displaystyle \mu } μ 1 {\displaystyle \mu _{1}} μ 2 {\displaystyle \mu _{2}} Σ {\displaystyle \Sigma } ↑ 推導基於乘法的協方差規則 cov ( A x , B y ) = A cov ( x , y ) B ⊤ {\displaystyle {\text{cov}}(Ax,By)=A{\text{cov}}(x,y)B^{\top }} cov ( x , y + z ) = cov ( x , y ) + cov ( x , z ) {\displaystyle {\text{cov}}(x,y+z)={\text{cov}}(x,y)+{\text{cov}}(x,z)} ↑ 例如,變換涉及將 1 = Σ1 /Σ1 相乘或新增 0 = Σ1 -Σ1 ,並相應地截斷逆矩陣。 ↑ Bar-Shalom, Yaakov; Campo, Leon (1986 年 11 月). “公共過程噪聲對雙感測器融合跟蹤協方差的影響”. 航空航天和電子系統 IEEE 彙刊 . AES-22 (6): 803–805. doi :10.1109/TAES.1986.310815 . ↑ 該策略對應於具有測量不確定性的後驗高斯過程,請參閱教科書 C. E. Rasmussen, C. K. I. Williams: 機器學習中的高斯過程 迴歸 中關於高斯過程迴歸的章節。 卡爾曼濾波器 也使用資料融合來分離訊號和測量不確定性。 ↑ C. E. Rasmussen, C. K. I. Williams: 機器學習中的高斯過程 從舊核心建立新核心。 第 94 頁。 ↑ C. E. Rasmussen, C. K. I. Williams: 機器學習中的高斯過程 貝葉斯模型選擇。 第 108 頁。 ↑ 資料可在 Google trends 中搜索“snowboard” 獲得。 












![{\displaystyle k(t,t'):=\operatorname {Cov} (X_{t},X_{t'}):=\mathbb {E} \left[(X_{t}-m(t))\cdot (X_{t'}-m(t'))\right],\quad t,t'\in T}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4aa08ac5d45b1abae6327583cdf7187d367347ff)

























































































![{\displaystyle \left[C_{XY}\right]{ij}=\left[\Sigma {XY}\right]{ij}/{\sqrt {\left[\Sigma _{X}\right]{ii}\left[\Sigma _{Y}\right]_{jj}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/418882ad152d96a36045cf137562d87ae433ea19)


















![{\displaystyle k(t,t')={\frac {1}{N-1}}\sum _{i=1}^{N}\left[f_{i}(t)-m(t)\right]\cdot \left[f_{i}(t')-m(t')\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96ecfed304ea5479c8616aafa1a8ace01e1606c2)
























![{\displaystyle X_{\text{U}}\mid X_{\text{K}}\sim {\mathcal {N}}\left(\mu _{\text{U}}+\Sigma _{\text{UK}}\left[\Sigma _{\text{KK}}+\mathbb {I} \sigma _{\text{noise}}^{2}\right]^{-1}(X_{\text{K}}-\mu _{\text{K}}),\Sigma _{\text{UU}}-\Sigma _{\text{UK}}\left[\Sigma _{\text{KK}}+\mathbb {I} \sigma _{\text{noise}}^{2}\right]^{-1}\Sigma _{\text{KU}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f17744af5b4e30dab6004fbd7f61cdfd3dc6b374)




































![{\displaystyle k(t,t')={\frac {1}{N-1}}\sum _{p=1}^{N}\left[f_{p}(t)-m(t)\right]\cdot \left[f_{p}(t')-m(t')\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f23777e5161267eaf143c21be846f58c2e93399)


















![{\displaystyle k(x,x')={\frac {1}{N-1}}\sum _{i=1}^{N}\left[f_{i}(x)-m(x)\right]\cdot \left[f_{i}(x')-m(x')\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/113d714d79833fc992f5e4342a985b43f7c40a4e)