兩年制學院代數預備課程/工作簿 AIE/比例推理
以下內容取自[1]。需要將其轉換為工作簿形式。
比例推理
比例是兩個量之間的數學關係。根據皮亞傑的智力發展理論,比例推理是兒童從具體運算階段發展到形式運算階段所獲得的技能之一。
“在數學和物理學中,比例是兩個量之間的數學關係。”這種“數學關係”有兩種不同的觀點;一種基於比率,另一種基於函式。
在許多教科書中,比例表示為兩個比率的等式
給出任何三個項的值,就可以解出第四個項。一旦學生掌握了這種算術技巧,人們就會認為學生理解了比例推理。然而,實驗資料表明情況可能並非如此。[需要引用]
科學家對比例有截然不同的看法。給定以下關於萬有引力定律的方程式(根據牛頓):
科學家會說,兩個物體之間的萬有引力與兩個物體的質量乘積成正比,與兩個物體之間距離的平方成反比。從這種角度來看,比例是數學方程式中變數之間的函式關係。
在皮亞傑的智力發展模型中,第四階段也是最後階段是形式運算階段。在讓·皮亞傑和巴貝爾·因海爾德合著的經典著作《從童年到青春期的邏輯思維的發展》中,形式運算推理採取了許多形式,包括命題推理、演繹邏輯、變數分離與控制、組合推理以及命題推理。羅伯特·卡普勒斯是 1960 年代和 1970 年代世界著名的科學教育家,他研究了青少年和成年人的所有這些推理形式,但他最出名的是他對比例推理的研究。
這是一張高先生和短先生的照片。
短先生身高六個回形針。如果用大紐扣測量,他身高四個大紐扣。
高先生與短先生相似,但身高六個大紐扣。
如果你可以用回形針測量高先生的高度,預測一下他的身高。解釋你的答案。
乘法推理 1:“他身高九個回形針。每個紐扣相當於一個半回形針。如果他身高六個紐扣,你乘以六乘以一個半得到九個回形針。”
乘法推理 2:“高先生比短先生高 1.5 倍。由於短先生身高 6 個回形針,高先生必須高 6 * 1.5 = 9 個回形針。”
使用加法的乘法推理:“每兩個紐扣有三個回形針。高先生比短先生高兩個紐扣,所以他必須高三個回形針。6 + 3 = 9 個回形針。”
加法推理 1:“高先生身高八個回形針。短先生身高四個大紐扣,六個回形針。所以紐扣比回形針少兩個。由於高先生和短先生相似,而且高先生身高六個紐扣,所以他身高必須是八個回形針。”
加法推理 2:“高先生比短先生高兩個紐扣,所以他也比短先生高兩個回形針,結果是八個回形針。”
估計:“九,我想他會高一點。”
雜亂無章:“由於高先生比短先生高兩個紐扣,我用六個回形針乘以二得到 12 個回形針。”
對於尚未達到形式運算推理階段的青少年或成年人來說,加法解法是最常見的。它是一種一致的、邏輯的策略,儘管不正確,而且對於問題中涉及的值來說,它會產生一個可信的答案。這似乎不是算術技能的問題,而是錯誤策略的應用。
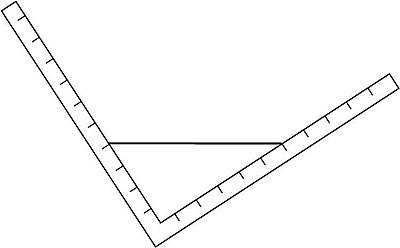
反比例存在類似的推理模式。考慮一個裝有彩色液體的容器,它位於一個直角三角形中,三角形可以傾斜,並且可以內建刻度測量左右兩側的水位。我們稱之為“水三角形”。
問題陳述和典型解決方案
[edit | edit source]旋轉你的水三角形,直到左側測量值為 4 個單位,右側測量值為 6 個單位。
假設三角形傾斜得更厲害,直到右側的水位達到 8 個單位。預測左側的水位將是多少個單位。
一個瞭解三角形面積的人可能會這樣推理:“最初,形成三角形的水的面積為 12,因為 ½ * 4 * 6 = 12。水的量不變,所以面積也不會變。所以答案是 3,因為 ½ * 3 * 8 = 12。”
正確的乘法答案相對較少。最常見的答案是:“2 個單位,因為右側的水位增加了 2 個單位,所以左側的水位必須減少 2 個單位,而 4 – 2 = 2。” 較少見的是,對 2 個單位的解釋是:“之前總共有 10 個單位,因為 4 + 6 = 10。單位總數必須保持不變,所以答案是 2,因為 2 + 8 = 10。”
因此,我們再次看到,處於非形式運算階段的人,在解決反比例問題時,採用的是加法策略,而不是乘法策略。而且,就像正比例一樣,這種錯誤的策略在個人看來似乎是合乎邏輯的,並且似乎給出了合理的答案。當學生實際進行實驗並傾斜三角形時,他們會發現答案是 3 而不是 2,他們會非常驚訝,因為他們之前非常自信地預測了答案。
將這些策略視為函式關係
[edit | edit source]令 T 為高個子先生的身高,S 為矮個子先生的身高,則正確的乘法策略可以表示為 T/S = 3/2;這是一個恆定比例關係。錯誤的加法策略可以表示為 T – S = 2;這是一個恆定差關係。以下是這兩個方程的影像。對於問題陳述中涉及的數值,這些影像“相似”,因此很容易理解為什麼人們認為他們的錯誤答案是完全合理的。
現在考慮我們使用“水三角形”的反比例。令 L 為左側的水位,R 為右側的水位,則正確的乘法策略可以表示為 L * R = 24;這是一個恆定積關係。錯誤的加法策略可以表示為 L + R = 10;這是一個恆定和關係。以下是這兩個方程的影像。對於問題陳述中涉及的數值,這些影像“相似”,因此很容易理解為什麼人們認為他們的錯誤答案是完全合理的。
比例推理的教學
[edit | edit source]正如任何經驗豐富的教師都能證明的那樣,僅僅告訴學生他的答案是錯誤的,然後指示學生使用正確的解決方案是不夠的。錯誤的策略並沒有“從大腦中去除”,並在完成當前課程後會再次出現。
此外,上面提到的加法策略不能簡單地標記為“錯誤”,因為它們確實與其他現實世界的情況相匹配。例如,考慮以下問題
今年的獨立日,高個子先生 6 歲,矮個子先生 4 歲。在未來的獨立日,矮個子先生 6 歲。在那個獨立日,高個子先生會幾歲?
類似地,恆定和關係在某些情況下可能是正確的。考慮以下問題。
河的左側有 4 只海狸,右側有 6 只海狸。在同一組海狸的後期,右側有 8 只海狸。左側將有幾隻海狸?
因此,在某些情況下,加法關係(恆定差和恆定和)是正確的,而在其他情況下,乘法關係(恆定比例和恆定積)是正確的。
動手活動和卡普拉斯學習迴圈的使用
[edit | edit source]至關重要的是,學生要自己認識到,他們目前的推理方式,例如加法,不適合他們試圖解決的乘法問題。羅伯特·卡普拉斯 開發了一個名為學習迴圈的學習模型,它促進了新的推理技能的習得。
1) 探索階段是第一個階段,在這個階段,學生透過他們自己的行動和反應來學習,幾乎沒有指導。學習環境必須經過精心設計,以將學生的注意力集中在相關問題上。如果學習者發現他們現有的策略與觀察到的結果不符,他們可能會經歷一些認知失調。這可能會導致他們無法用目前的思想或推理模式回答的問題。
2) 在第二個階段,介紹和解釋概念。在這裡,教師更積極,學習是透過解釋來完成的。
3) 最後,在第三階段,將概念應用於新情況,並擴充套件其適用範圍。學習是透過重複和練習來實現的,以便新的想法和思維方式有時間穩定下來。
動手活動在學習迴圈中非常有用。在預測高個子先生用回形針的身高後,可以引入測量工具,學生可以測試他們的策略。對於使用恆定差關係的學生來說,實際測量將表明高個子先生實際上有 9 個回形針高,這將產生一些認知失調。
反比例也是如此。這是一張兩位學生使用“水三角形”的照片。鑑於上述問題,大多數學生預測當水三角形傾斜時,左側的水位將下降到 2 個單位。當他們進行實驗並看到答案是 3 個單位時,就會產生一些認知失調。這是教師將課程轉移到學習迴圈第二階段的最佳時機。
重要的是,學生不要過度應用他們學到的乘法策略。因此,一些動手活動可能不是基於乘法關係。這是一張兩位學生使用恆定和關係正確的裝置的照片。
並非總是有可能或可行地將精心設計的動手活動交到學生手中。此外,年長的受眾並不總是對使用動手實驗做出積極的反應。但是,通常可以透過思維實驗來引入認知失調。
透過思維實驗確定正確的關係
[edit | edit source]在上面提到的所有實驗中,有兩個變數的值根據固定的關係而變化。考慮以下類似於高個子先生和矮個子先生問題的題目。
這是一張父親和女兒的照片。在這張照片中,女兒高 4 釐米,父親高 6 釐米。他們決定放大照片,在更大的照片中,女兒高 6 釐米。父親在較大的照片中有多高?
對於使用加法關係的個人來說,一個非常常見的答案是 8 釐米,因為父親總是比女兒高 2 釐米。所以現在問問這位學生以下問題
假設他們製作了原始照片的一個非常小的版本,在這個小版本中,父親高 2 釐米。女兒在這個小版本中有多高?
學生很快意識到“父親總是比女兒高 2 釐米”的策略是不正確的。這也可以透過探索另一個極端來實現,其中將原始照片放大到海報大小,女兒高 100 釐米。父親在這個海報中有多高?一個回答 102 釐米的學生意識到父親和女兒幾乎一樣高,這是不可能的。一旦認知失調出現,教師就可以引入正確的關係,即恆定比例。
也可以鼓勵學生進行自己的思維實驗,例如“如果女兒的身高在放大時翻倍,父親的身高會發生什麼?”大多數學生,包括那些仍然處於具體運算階段的學生,會很快回答說父親的身高也必須翻倍。抽象的思維實驗是:“假設其中一個變數的值翻倍,另一個變數會如何變化?”如果答案是“翻倍”,那麼這可能是一個恆定比例問題。但是,如果答案不是翻倍,例如上面給出的高個子先生和矮個子先生的年齡問題,那麼它就不是一個恆定比例問題。
對於反向關係,例如“水三角形”,極限情況也會造成認知失調。例如,給定初始條件,左側水位為 4 個單位,右側水位為 6 個單位,問如果將三角形傾斜到右側水位為 10 個單位,左側水位會是多少?學生此時會放棄加法策略,意識到 0 不可能是正確答案。對於反向關係,可以進行一個思維實驗。如果一個變數的值加倍,另一個變數會發生什麼變化?如果答案是 1/2,那麼這可能是一個恆定乘積關係(即反比例)。
繪製變數的值也可以是一個有價值的工具,用於識別兩個變數是否成正比。如果它們成正比,那麼這些值應該在一條直線上,並且這條直線應該與原點相交。
上面提到的四種函式關係,恆定和、恆定差、恆定積和恆定比,是基於學生最熟悉的四種算術運算,即加、減、乘、除。現實世界中的大多數關係並不屬於這些類別之一。但是,如果學生學習簡單的技術,例如思維實驗和繪製圖表,他們將能夠將這些技術應用於更復雜的情況。
再次考慮牛頓萬有引力定律
如果學生理解變數之間的函式關係,那麼他/她應該能夠回答以下思維實驗。
如果發生以下情況,萬有引力會發生什麼變化?
- 其中一個質量加倍?
- 一個質量加倍,另一個質量減半?
- 兩個質量都加倍?
- 兩個質量都減半?
- 兩個質量之間的距離加倍?
- 兩個質量之間的距離減半?
最後要提醒的是:思維實驗必須透過實驗結果來驗證。考慮以下變數:物體的質量和它落向地球的速度。當被要求進行思維實驗時,許多兒童和成人可能會說,當質量加倍時,物體將以兩倍的速度下落。然而,實驗結果並不支援這種“邏輯”思維實驗。因此,理論結果與實驗資料一致始終是必不可少的。