金融原理/第一部分/第七章/資本資產定價模型

道瓊斯工業平均指數在3年內每月資料的CAPM和證券市場線（紫色）的估計。

在金融領域，資本資產定價模型（CAPM）用於確定資產在加入已充分多元化的投資組合時的理論上適當的必要回報率，前提是該資產具有不可分散風險。該模型考慮了資產對不可分散風險的敏感性（也稱為系統性風險或市場風險），金融行業通常用β（β）表示，以及市場的預期回報和理論無風險資產的預期回報。

該模型由Jack Treynor（1961，1962）、 William Sharpe（1964）、John Lintner（1965a，b）和Jan Mossin（1966）獨立提出，其基礎是Harry Markowitz早期的多元化和現代投資組合理論研究。Sharpe、Markowitz和Merton Miller因對金融經濟學領域的貢獻而共同獲得了諾貝爾經濟學獎。

公式

檔案:SecMktLine.png 證券市場線，如圖形所示，描述了β與資產預期回報率之間的關係。

CAPM是用於對單個證券或投資組合進行定價的模型。對於單個證券，我們利用證券市場線 (SML) 及其與預期回報和系統性風險 (β) 之間的關係來表明市場必須如何根據其安全風險類別對單個證券進行定價。SML 使我們能夠計算任何證券的風險回報率與整個市場的風險回報率之間的關係。因此，當任何證券的預期回報率除以其β係數時，市場中任何單個證券的風險回報率等於市場風險回報率，因此

${\frac {E(R_{i})-R_{f}}{\beta _{i}}}=E(R_{m})-R_{f}$

市場風險回報率實際上是市場風險溢價，透過重新排列上面的等式並求解E(Ri)，我們得到了資本資產定價模型 (CAPM)。

$E(R_{i})=R_{f}+\beta _{i}(E(R_{m})-R_{f})\,$

其中

• $E(R_{i})~~$是資本資產的預期回報
• $R_{f}~$是無風險利率，例如政府債券產生的利息
• $\beta _{i}~~$（beta）是預期超額資產回報對預期超額市場回報的敏感性，或者$\beta _{i}={\frac {\mathrm {Cov} (R_{i},R_{m})}{\mathrm {Var} (R_{m})}}$,
• $E(R_{m})~$是市場的預期回報
• $E(R_{m})-R_{f}~$有時被稱為市場溢價（預期市場回報率與無風險回報率之間的差值）。
• $E(R_{i})-R_{f}~$ 也被稱為 *風險溢價*。

換句話說，從風險溢價的角度來看，我們發現

$E(R_{i})-R_{f}=\beta _{i}(E(R_{m})-R_{f})\,$

這表明 *個體風險溢價* 等於 *市場溢價* 乘以 *β*。

注意 1：市場預期回報率通常透過測量市場投資組合（例如標準普爾 500 指數）的歷史回報的幾何平均值來估算。

注意 2：用於確定風險溢價的無風險回報率通常是歷史無風險回報率的算術平均值，而不是當前無風險回報率。

有關完整的推導，請參見現代投資組合理論。

證券市場線

SML 本質上是資本資產定價模型 (CAPM) 公式結果的圖表。*x* 軸代表風險 (beta)，*y* 軸代表預期回報。市場風險溢價由 SML 的斜率決定。

β 和要求回報之間的關係繪製在 *證券市場線* (SML) 上，該線顯示了預期回報作為 β 的函式。截距是市場上可獲得的名義無風險利率，而斜率是市場溢價，E(R_m)− R_f。證券市場線可以被視為代表資產價格的單因素模型，其中 Beta 是對市場價值變化的敞口。因此，SML 的方程式為

$\mathrm {SML} :E(R_{i})=R_{f}+\beta _{i}(E(R_{M})-R_{f}).~$

這是一個有用的工具，用於確定正在考慮納入投資組合的資產是否提供了合理的風險預期回報。單個證券繪製在 SML 圖表上。如果證券的預期回報與風險繪製在 SML 以上，則該證券被低估，因為投資者可以預期從固有的風險中獲得更高的回報。而繪製在 SML 以下的證券被高估，因為投資者會接受較低的回報以換取承擔的風險。

資產定價

一旦使用 CAPM 計算出預期/要求回報率，$E(R_{i})$，我們可以將此要求回報率與資產在特定投資期限內的估計回報率進行比較，以確定其是否為合適的投資。要進行此比較，您需要根據 **基本面分析或技術分析技術**（包括市盈率、市淨率等）對證券的回報前景進行獨立估計。

假設 CAPM 是正確的，當估計價格與資產未來現金流的現值相同時，資產的價格是正確的，該現值以 CAPM 建議的比率貼現。如果估計價格高於 CAPM 估值，則該資產被低估（而當估計價格低於 CAPM 估值時被高估）。 當資產不在 SML 上時，這也可能表明定價錯誤。由於資產在時間 $t$ 的預期回報是 $E(R_{t})={\frac {E(P_{t+1})-P_{t}}{P_{t}}}$，比 CAPM 建議的預期回報率更高表明 $P_{t}$ 太低（該資產目前被低估），假設在時間 $t+1$ 該資產恢復到 CAPM 建議的價格。

使用 CAPM 的資產價格 $P_{0}$，有時被稱為確定性等價定價公式，是一個線性關係，由下式給出

$P_{0}={\frac {1}{1+R_{f}}}\left[E(P_{T})-{\frac {\mathrm {Cov} (P_{T},R_{M})(E(R_{M})-R_{f})}{\mathrm {Var} (R_{M})}}\right]$

其中 $P_{T}$ 是資產或投資組合的收益。

資產特定要求回報

CAPM 返回資產適當的必要回報或折現率，即考慮到資產的相對風險性，應按該比率折現資產產生的未來現金流。高於 1 的貝塔係數表示風險高於平均水平；低於 1 的貝塔係數表示風險低於平均水平。因此，風險較高的股票將具有更高的貝塔係數，並以更高的比率折現；風險較低的股票將具有較低的貝塔係數，並以較低的比率折現。鑑於公認的凹型效用函式，CAPM 與直覺一致 - 投資者（應該）要求更高的回報來持有風險較高的資產。

由於貝塔係數反映了資產對不可分散的（即市場）風險的特定敏感性，因此整個市場（按定義）的貝塔係數為 1。股票市場指數通常用作市場的區域性代理 - 在這種情況下（按定義）貝塔係數為 1。因此，一個大型多元化投資組合（如共同基金）的投資者預計表現將與市場一致。

風險和多元化

投資組合的風險包括系統性風險（也稱為不可分散風險）和非系統性風險（也稱為特質風險或可分散風險）。系統性風險是指所有證券共有的風險，即市場風險。非系統性風險是與單個資產相關的風險。透過在投資組合中包含更多資產，非系統性風險可以分散到更小的水平（特定風險“平均化”)。在一個市場內，系統性風險無法以同樣的方式分散。根據市場的不同，在英國或美國等發達市場，一個大約 30-40 種證券的投資組合將使投資組合充分多元化，以至於風險敞口僅限於系統性風險。在發展中國家，由於資產波動性較高，需要更多數量的證券。

理性的投資者不應該承擔任何可分散的風險，因為在這個模型的範圍內，只有不可分散的風險才會得到回報。因此，資產的必要回報，即補償所承擔風險的回報，必須與它在投資組合中的風險性相關聯 - 即它對整體投資組合風險性的貢獻 - 而不是它“獨立風險性”。在 CAPM 的背景下，投資組合風險用更高的方差（即更低的可預測性）來表示。換句話說，投資組合的貝塔係數是衡量投資者承擔的系統性敞口回報的決定因素。

有效邊界

(馬科維茨) 有效邊界。CAL 代表資本配置線。

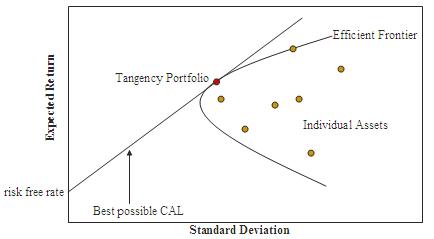
CAPM 假設投資組合的風險回報狀況可以最佳化 - 最佳投資組合在回報水平方面顯示出最低可能的風險水平。此外，由於新增到投資組合中的每項額外資產都會進一步分散投資組合，因此最佳投資組合必須包含所有資產（假設沒有交易成本），並且每個資產的價值加權以實現上述目標（假設任何資產都是無限可分的）。所有這些最佳投資組合，即每個回報水平的一個，構成有效邊界。

由於非系統性風險是可分散的，因此投資組合的總風險可以視為貝塔係數。

市場投資組合

投資者可以選擇將其財富的一部分投資於風險資產組合，其餘部分投資於現金 - 以無風險利率賺取利息（或者實際上可以借錢來為其購買風險資產提供資金，在這種情況下，現金權重為負）。在這裡，風險資產與無風險資產的比例不決定總回報 - 這種關係顯然是線性的。因此，可以透過兩種方式實現特定回報

1. 將全部財富投資於風險投資組合，
2. 或將一部分投資於風險投資組合，其餘部分投資於現金（借入或投資）。

然而，對於給定的回報水平，這些投資組合中只有一個是最優的（從最低風險的角度而言）。由於無風險資產（按定義）與任何其他資產不相關，因此選項 2 通常具有較低的方差，因此是兩種選項中更有效的一個。

這種關係也適用於有效邊界上的投資組合：對於較低的回報水平，較高回報投資組合加上現金比僅有較低迴報投資組合更有效。對於給定的無風險利率，只有一個最優投資組合可以與現金相結合，以在任何可能的回報下實現最低的風險水平。這就是市場投資組合。

CAPM 的假設

所有投資者： Template:Unreferenced section

1. 旨在最大化經濟效用。
2. 是理性的，並且厭惡風險。
3. 在各種投資中實現廣泛多元化。
4. 是價格接受者，即他們無法影響價格。
5. 可以以無風險利率借入和借出無限金額。
6. 在沒有交易或稅收成本的情況下進行交易。
7. 處理所有可高度分割成小部分的證券。
8. 假設所有資訊都同時提供給所有投資者。

此外，該模型假設過去回報的標準差是與給定證券相關的未來風險的完美替代指標。

CAPM 的問題

• 該模型假設回報的方差是風險的充分衡量指標。這將由回報呈正態分佈的假設所暗示，或者確實，以任何雙引數方式分佈，但對於一般的回報分佈，其他風險衡量指標（如相干風險衡量指標）將更充分地反映活躍和潛在股東的偏好。事實上，金融投資中的風險本身並不是方差，而是虧損的可能性：它本質上是不對稱的。
• 該模型假設所有活躍和潛在股東都能獲得相同的資訊，並且同意所有資產的風險和預期回報（同質預期假設）。
• 該模型假設活躍和潛在股東的機率信念與回報的真實分佈相匹配。另一種可能性是，活躍和潛在股東的預期是有偏見的，導致市場價格資訊效率低下。這種可能性在行為金融領域被研究，該領域使用心理假設來提供 CAPM 的替代方案，例如肯特·丹尼爾、大衛·希爾斯利弗和阿瓦尼達爾·蘇布拉馬尼亞姆（2001 年）的過度自信資產定價模型。
• 該模型似乎無法充分解釋股票回報的變化。實證研究表明，低貝塔係數股票可能比模型預測的提供更高的回報。這種資料最早在 1969 年紐約布法羅的一次會議上由菲舍爾·布萊克、邁克爾·詹森和邁倫·斯科爾斯在一篇論文中提出。要麼這個事實本身是理性的（這將拯救有效市場假說，但使 CAPM 錯誤），要麼它是不理性的（這將拯救 CAPM，但使 EMH 錯誤 - 事實上，這種可能性使波動率套利成為可靠地擊敗市場的一種策略）。
• 該模型假設，在給定的預期回報下，活躍和潛在股東會更傾向於較低的風險（較低的方差）而不是較高的風險，反之亦然，在給定的風險水平下，會更傾向於較高的回報而不是較低的回報。它不允許存在願意為更高風險接受較低迴報的活躍和潛在股東。賭場賭徒付費以承擔更多風險，並且有可能一些股票交易者也會為風險付費。
• 該模型假設沒有稅收或交易成本，儘管這個假設可以透過更復雜的模型版本來放寬。
• 市場投資組合由所有市場中的所有資產組成，其中每個資產的權重與其市值成正比。這假設個人活躍和潛在股東對市場和資產沒有偏好，並且活躍和潛在股東僅根據其風險回報狀況選擇資產。它還假設所有資產都是無限可分的，可以持有或交易的量沒有限制。
• 理論上，市場組合應該包含所有由任何人作為投資持有的資產型別（包括藝術品、房地產、人力資本等等）。實際上，這種市場組合是不可觀察的，人們通常用股票指數來代替真實的市場組合。不幸的是，已經證明這種替代並非無害，它會導致對資本資產定價模型有效性的錯誤推斷，並有人指出，由於真實市場組合的不可觀察性，資本資產定價模型可能無法在經驗上進行檢驗。這在理查德·羅爾 1977 年發表的一篇論文中得到了更深入的論述，通常被稱為羅爾批判。
• 該模型假設經濟主體在短期內進行最佳化，事實上，具有長期視野的投資者會最優地選擇長期通脹掛鉤債券而不是短期利率，因為對於這樣的主體來說，這將是更無風險的資產。
• 該模型只假設兩個日期，因此沒有機會隨著時間的推移反覆消費和重新平衡投資組合。該模型的基本見解在羅伯特·默頓的跨期資本資產定價模型（ICAPM） 和道格拉斯·布里登和馬克·魯賓斯坦的消費資本資產定價模型（CCAPM） 中得到了擴充套件和推廣。
• CAPM 假設所有活躍的和潛在的股東都會考慮他們所有的資產並最佳化一個投資組合。這與個人股東持有的投資組合形成鮮明對比：人類往往擁有分散的投資組合，或者更確切地說，是多個投資組合：每個目標一個投資組合——參見行為投資組合理論 和馬斯洛投資組合理論。
• 實證檢驗表明市場存在諸如規模效應和價值效應之類的異常現象，這些現象無法用 CAPM 解釋。 更多詳情請參見法瑪-弗蘭奇三因子模型。

參考文獻

• Black, Fischer., Michael C. Jensen, 和 Myron Scholes (1972)。資本資產定價模型：一些實證檢驗，第 79–121 頁，M. Jensen 編輯，《資本市場理論研究》。紐約：普萊格出版社。
• Fama, Eugene F. (1968)。風險、收益和均衡：一些澄清性評論。金融雜誌第 23 卷，第 1 期，第 29–40 頁。
• Fama, Eugene F. 和 Kenneth French (1992)。預期股票收益的橫截面。金融雜誌，1992 年 6 月，427-466。
• French, Craig W. (2003)。Treynor 資本資產定價模型，投資管理雜誌，第 1 卷，第 2 期，第 60–72 頁。可在 http://www.joim.com/ 獲取。
• French, Craig W. (2002)。Jack Treynor 的“關於風險資產的市場價值理論”（12 月）。可在 http://ssrn.com/abstract=628187 獲取。
• Lintner, John (1965)。風險資產的估值以及股票投資組合和資本預算中風險投資的選擇，經濟學與統計學評論，47 (1)，13-37。
• Markowitz, Harry M. (1999)。投資組合理論的早期歷史：1600-1960，金融分析師雜誌，第 55 卷，第 4 期。
• Mehrling, Perry (2005)。Fischer Black 和金融的革命性思想。霍博肯：約翰·威利父子公司。
• Mossin, Jan. (1966)。資本資產市場的均衡，計量經濟學，第 34 卷，第 4 期，第 768–783 頁。
• Ross, Stephen A. (1977)。資本資產定價模型 (CAPM)、賣空限制及相關問題，金融雜誌，32 (177)
• Rubinstein, Mark (2006)。投資理論史。霍博肯：約翰·威利父子公司。
• Sharpe, William F. (1964)。資本資產價格：風險條件下市場均衡理論，金融雜誌，19 (3)，425-442
• Stone, Bernell K. (1970) 風險、收益和均衡：資產選擇和資本市場均衡的通用單期理論。劍橋：麻省理工學院出版社。
• Tobin, James (1958)。流動性偏好作為對風險的態度，經濟研究評論，25
• Treynor, Jack L. (1961)。市場價值、時間和風險。未出版手稿。
• Treynor, Jack L. (1962)。關於風險資產的市場價值理論。未出版手稿。最終版本發表於 1999 年，收錄於資產定價和投資組合表現：模型、策略和表現指標。羅伯特·A·科拉奇克（編輯）倫敦：風險書籍，第 15–22 頁。
• Mullins, David W. (1982)。資本資產定價模型有效嗎？，哈佛商業評論，1982 年 1 月至 2 月，105-113。

外部連結

• 多資產有效邊界